1 Introduction

The precise measurements on the atmospheric, solar, accelerator and reactor neutrinos have established the phenomenon of neutrino oscillations. This fact implies three flavors of neutrinos should be massive and mixed [1]. Meanwhile, the cosmological observations indicate the neutrinos should be extremely light [1]. The tiny but nonzero neutrino masses call for new physics beyond the \(SU(3)_c^{}\times SU(2)_L^{}\times U(1)^{}_{Y}\) standard model (SM). Furthermore, the SM is challenged by other puzzles such as the cosmic baryon asymmetry [1]. Currently a seesaw [2,3,4,5] extension of the SM has become very attractive since it can simultaneously explain the small neutrino masses and the cosmic baryon asymmetry [6]. In this popular scenario [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22], we do not know much about the masses and couplings involving the non-SM fields. Consequently, we cannot get an exact relation between the cosmic baryon asymmetry and the neutrino mass matrix. For example, we can expect a successful leptogenesis in the canonical seesaw model even if the neutrino mass matrix does not contain any CP phases [23].

In a previous paper [28], we showed that the cosmic baryon asymmetry could be well described by the Dirac neutrino mass matrix, the charged lepton masses and the heavy mirror charged lepton masses within a mirror left-right symmetric framework based on the gauge groups \(SU(3)^{}_{c}\times SU(2)^{}_{L}\times SU(2)^{}_{R}\times U(1)_X^{}\) [29,30,31,32]. However, we had to introduce several scalars irrelevant to the neutrino mass generation so that we could eliminate some harmful lepton asymmetries. The model thus seemed complicated and uneconomical.

In the present paper, we shall develop a novel leptogenesis [6] scenario where the neutrinos can obtain their tiny Majorana masses in the so-called linear [25,26,27] seesaw way while the cosmic baryon asymmetry can be parameterized by the neutrino and charged lepton mass matrices as well as the heavy mirror charged lepton masses. This scenario shares some features of the work [28]. For example, it is also in the mirror left-right symmetric framework. However, this model does not contain any particles irrelevant to the neutrino mass generation. Specifically, some Yukawa interactions can accommodate the lepton-number-conserving decays of the mirror electron-positron pairs to produce three individual lepton asymmetries in the ordinary lepton flavors although the lepton number is exactly conserved. The same Yukawa interactions can participate in the Majorana neutrino mass generation and then can lead to some lepton-number-violating processes to wash out part of the produced lepton asymmetries. The \(SU(2)_L^{}\) sphaleron [33] processes then can partially convert the remnant lepton asymmetries to a baryon asymmetry.

2 The model

We extend the SM fermions and Higgs scalar, i.e.

$$\begin{aligned}&q^{}_{L}\left( 2,1,+\frac{1}{3}\right) (+1), \,\, d^{}_{R}\left( 1,1,-\frac{2}{3}\right) (+1),\nonumber \\&\quad u^{}_{R}\left( 1,1,+\frac{4}{3}\right) (+1), l^{}_{L}(2,1,-1)(-1),\,\, l^{}_{L}(2,1,-1)(-1), \nonumber \\&\quad e^{}_{R}(1,1,-2)(-1); \phi ^{}_L(2,1,-1)(0), \end{aligned}$$
(1)

by a mirror copy [28, 34,35,36,37,38,39,40,41,42,43,44,45],

$$\begin{aligned}&Q^{}_{R}\left( 1,2,+\frac{1}{3}\right) (-1),\,\, D^{}_{L}\left( 1,1,-\frac{2}{3}\right) (-1),\nonumber \\&\quad U^{}_{L}\left( 1,1,+\frac{4}{3}\right) (-1),\,\,L^{}_{R}(1,2,-1)(+1), \nonumber \\&\quad E^{}_{L}(1,1,-2)(+1); \phi ^{}_R(1,2,-1)(0). \end{aligned}$$
(2)

Here and thereafter the first brackets following the fields describe the transformations under the \(SU(2)^{}_{L}\times SU(2)_R^{}\times U(1)_X^{}\) gauge groups, while the second brackets denote an imposed \(U(1)_{3B-L}^{}\) global symmetry. Note the SM fields have a \(U(1)_{3B-L}^{}\) charge opposite to their mirror partners. Our model also contains the Higgs scalars \(\chi _{L,R}^{}\), \(\Sigma \), \(\xi \) and the fermions \(N_L^{}\) as below,

$$\begin{aligned}&\chi ^{}_L(2,1,-1)(-2), \chi ^{}_R(1,2,-1)(+2), \Sigma (2,2,0)(-2),\nonumber \\&\xi (1,1,0)(+1); N^{}_L(1,1,0)(-1). \end{aligned}$$
(3)

The Higgs bidoublet \(\Sigma \) can be expressed in terms of two \(SU(2)_L^{}\) doublets, i.e. \(\Sigma =\left[ \sigma _1^{}~{\tilde{\sigma }}_2^{}\right] \).

The usual electric charge Q and hypercharge Y are related to the \(SU(2)^{}_{L}\times SU(2)_R^{}\times U(1)_X^{}\) quantum numbers as [29,30,31,32],

$$\begin{aligned} Y= T_{3R}^{} + \frac{X}{2},\quad Q=T_{3L} +T_{3R}^{} + \frac{X}{2} =T_{3L} +Y \,, \end{aligned}$$
(4)

where \(T_{3L(R)}^{}=0\) for the \(SU(2)_{L(R)}^{}\) singlets, \(T_{3L(R)}^{}=+1/2\) for the up components of the \(SU(2)_{L(R)}^{}\) doublets, while \(T_{3L(R)}^{}=-1/2\) for the down components. So, we can easily read the hypercharges of the fermions and scalars after the \(SU(2)_L^{}\times SU(2)_R^{}\times U(1)_X^{}\) symmetry is spontaneously broken down to the SM \(SU(2)_L^{}\times U(1)_Y^{}\) symmetry. For example, the SM fermions and Higgs scalar \((q^{}_L, d_R^{}, u_R^{}, l_L^{}, e_R^{}, \phi ^{}_L)\) have their hypercharges \((+\frac{1}{6}, -\frac{1}{3}, +\frac{2}{3}, -\frac{1}{2}, -1,-\frac{1}{2})\) as they are in the SM.

In this work, the discrete left-right symmetry is taken to be a mirror CP (charge conjugation and parity) symmetry:

$$\begin{aligned}&\phi _L^{}{\mathop {\longleftrightarrow }\limits ^{CP}}\phi _{R}^{*},\quad \chi _L^{}{\mathop {\longleftrightarrow }\limits ^{CP}}\chi _{R}^{*}, \quad \Sigma {\mathop {\longleftrightarrow }\limits ^{CP}}\Sigma ^T_{},\quad \xi {\mathop {\longleftrightarrow }\limits ^{CP}} \xi \,,\nonumber \\&q_{L}^{}{\mathop {\longleftrightarrow }\limits ^{CP}}Q_{R}^{c},\quad d_{R}^{}{\mathop {\longleftrightarrow }\limits ^{CP}}D_{L}^{c}, \quad u_{R}^{}{\mathop {\longleftrightarrow }\limits ^{CP}}U_{L}^{c},\nonumber \\&l_{L}^{}{\mathop {\longleftrightarrow }\limits ^{CP}}L_{R}^{c},\quad e_{R}^{}{\mathop {\longleftrightarrow }\limits ^{CP}}E_{L}^{c},\quad N_{L}^{}{\mathop {\longleftrightarrow }\limits ^{CP}}N_{L}^{}. \end{aligned}$$
(5)

The global \(U(1)_{3B-L}^{}\) symmetry and the discrete mirror CP symmetry are both conserved exactly.

For simplicity we do not write down the full scalar potential. Instead we show the cubic terms and some quartic terms as below,

$$\begin{aligned}&V\supset \kappa \xi ^2_{} \left( \phi ^\dagger _{L} \chi _L^{} +\phi ^T_R \chi ^{*}_R\right) +\rho \left( \phi ^\dagger _L \Sigma \chi ^{}_R \right. \nonumber \\&\left. \quad + \phi ^T_R \Sigma ^T_{} \chi ^{*}_L\right) +\text {H.c.}. \end{aligned}$$
(6)

As for the Yukawa interactions, they are given by

$$\begin{aligned} {\mathcal {L}}_Y^{}= & {} -y^{}_d \left( {\bar{q}}^{}_L {\tilde{\phi }}^{}_{L} d^{}_R + {\bar{Q}}^c_R {\tilde{\phi }}^*_{R} D^{c}_L \right) \nonumber \\&-y^{}_u \left( {\bar{q}}^{}_L \phi ^{}_{L} u^{}_R + {\bar{Q}}^c_R \phi ^*_{R} U^{c}_L \right) - y_Q^{}{\bar{q}}^{}_L {\tilde{\Sigma }} Q_R^{}\nonumber \\&-y^{}_e \left( {\bar{l}}^{}_L {\tilde{\phi }}^{}_{L} e^{}_R + {\bar{L}}^c_R {\tilde{\phi }}^*_{R} E^{c}_L \right) \nonumber \\&-y^{}_N \left( {\bar{l}}^{}_L \chi ^{}_{L} N^{c}_L + {\bar{L}}^c_R \chi ^*_R N^{c}_L \right) - y_L^{} {\bar{l}}_L^{} \Sigma L_R^{}+\text {H.c.}\nonumber \\&\quad \text {with}~~y_Q^{}=y_Q^T,\quad y_L^{}=y_L^T. \end{aligned}$$
(7)

Note the \(U(1)_{3B-L}^{}\) global symmetry has forbidden the gauge-invariant mass terms of the [SU(2)]-singlet fermions.

We would like to give some comments on the original models for linear seesaw [25,26,27]. In these models, three gauge-singlet fermions, i.e. the \(N_L^{}\) fermions in our model, can always have a Majorana mass term and hence the left-handed neutrinos can always obtain their Majorana masses through an inverse/double seesaw besides the linear seesaw [25,26,27]. There are no symmetries constraining the size of this Majorana mass term. Accordingly, although the linear seesaw is allowed to dominate over the inverse/double seesaw, such choice can not be explained by certain symmetries. Moreover, these models can accommodate a conventional leptogenesis scenario. As we will demonstrate in the following, our model provides a purely linear seesaw and a new leptogenesis scenario.

3 Fermion masses

From the full potential which are not shown for simplicity, we can expect the VEVs to be

$$\begin{aligned} \langle \xi \rangle , ~ \langle \chi _R^{0}\rangle ,~\langle \phi _R^{0} \rangle \gg \langle \phi _L^{0}\rangle ,~\langle \chi _L^{0} \rangle , ~\langle \sigma _{1,2}^{0} \rangle . \end{aligned}$$
(8)

For example, after \(\xi \) and \(\chi _R^{}\) develop their VEVs, \(\phi _R\) can obtain a VEV due to the second term in Eq. (6). Subsequently, \(\sigma _1^{}\) develops its VEV and then \(\phi _L^{}\) and \(\chi _L^{}\) can acquire their VEVs through the third and forth terms in Eq. (6). The hierarchical VEVs (8) can only give a negligible effect on the precision measurements such as the \(W-W'\) and \(Z-Z'\) mixing.

The Yukawa interactions (7) then can reasonably yield

$$\begin{aligned}&y_Q^{} \langle \sigma _{2}^{0} \rangle \ll y_{d}^{} \langle \phi _R^{0} \rangle ,\quad y_Q^{} \langle \sigma _{1}^{0} \rangle \ll y_{u}^{} \langle \phi _R^{0} \rangle \,, \nonumber \\&y_L^{} \langle \sigma _{2}^{0} \rangle \ll y_{e}^{} \langle \phi _R^{0} \rangle ,\quad y_L^{} \langle \sigma _{1}^{0} \rangle \ll y_{N}^{} \langle \chi _R^{0} \rangle . \end{aligned}$$
(9)

This means the mixing between the ordinary charged fermions \((f=d,u,e)\) and their mirror partners \((F=D,U,E)\) should be of the order of \({\mathcal {O}}(y_{Q,L}^{}\langle \sigma _{1,2}^{0}\rangle /M_F^{}) \ll 1\) and hence can be safely ignored. Thus the mass eigenstates of the charged fermions can come from

$$\begin{aligned}&{\mathcal {L}}\supset - m_f^{} {\bar{f}}_L^{} f_R^{} - M_F^{} {\bar{F}}_R^{c} F_L^{c}+ \text {H.c.}~~\text {with}\nonumber \\&\quad m_f^{}=y_{f}^{} \langle \phi _L^{0} \rangle \ll M_F^{}=y_{f}^{} \langle \phi _R^{0} \rangle . \end{aligned}$$
(10)

Meanwhile, we can apply the linear seesaw mechanism [25,26,27] to the neutral fermions, i.e.

$$\begin{aligned}&{\mathcal {L}}\supset -\left[ {\bar{\nu }}_L^{}~ {\bar{N}}_L^{} ~ {\bar{N}}_R^{c}\right] \!\!\left[ \begin{array}{ccc} 0 &{}y_N^{} \langle \chi _L^0 \rangle &{} y_L^{} \langle \sigma _1^0 \rangle \\ y_N^T \langle \chi _L^0\rangle &{} 0&{} y_N^{T} \langle \chi _R^0 \rangle \\ Y_L^T\langle \sigma _1^0\rangle &{} y_N^{} \langle \chi _R^0 \rangle &{} 0 \end{array}\right] \!\!\! \left[ \begin{array}{c}\nu _L^{c}\\ N_L^{c}\\ N_R^{}\end{array}\right] +\text {H.c.}\nonumber \\&\quad \simeq \!- M_N^{} {\bar{N}}_R^{c}N_L^{c} -\frac{1}{2} m_\nu ^{} {\bar{\nu }}_L^{} \nu _L^c +\text {H.c.}~~\text {with}\nonumber \\&\quad M_N^{}=y_{N}^{} \langle \chi _R^{0} \rangle ,\quad m_\nu ^{} =m_\nu ^T= -2 y_L^{} \langle \sigma _1^{0} \rangle \frac{ \langle \chi _L^{0} \rangle }{ \langle \chi _R^{0} \rangle }. \end{aligned}$$
(11)

Here \(N_R^{}\) denotes the neutral components of the \(SU(2)_R^{}\) doublets \(L_R^{}\).

Note the VEVs \(\langle \phi _{L}^{0} \rangle \), \(\langle \chi _{L}^{0} \rangle \) and \(\langle \sigma _{1,2}^{0} \rangle \), should be constrained by

$$\begin{aligned}&\sqrt{ \langle \phi _{L}^{0} \rangle ^2_{} + \langle \chi _{L}^{0} \rangle ^2_{} + \langle \sigma _{1}^{0} \rangle ^2_{} + \langle \sigma _{2}^{0} \rangle ^2_{}}\equiv v =174\,\text {GeV},\nonumber \\&\langle \phi _{L}^{0} \rangle = \frac{m_t^{}}{y_t^{}}> \frac{m_t^{}}{\sqrt{4\pi }}\simeq 48.5\,\text {GeV}, \end{aligned}$$
(12)

which implies

$$\begin{aligned} \mu _2^{2}\equiv & {} 2\langle \chi _{L}^{0} \rangle \langle \sigma _{1}^{0}\rangle \le \langle \chi _{L}^{0} \rangle ^2_{}+ \langle \sigma _{1}^{0} \rangle ^2_{} < \left( 174^2- 48.5^2\right) \,\text {GeV}^2_{} \nonumber \\= & {} 2.79\times 10^4_{}\,\text {GeV}^2_{}. \end{aligned}$$
(13)

In addition, the tiny but nonzero neutrino masses require

$$\begin{aligned} \mu _1^{}\equiv & {} \frac{ 2\langle \chi _{L}^{0} \rangle \langle \sigma _{1}^{0}\rangle }{ \langle \chi _{R}^{0} \rangle } = \frac{ {\hat{m}}_\nu ^{}}{{\hat{y}}_L^{}}> \frac{ m_{\text {max}}^{}}{\sqrt{4\pi }}\nonumber \\= & {} 0.014\,\text {eV} \left( \frac{m_{\text {max}}^{}}{0.05\,\text {eV}}\right) , \end{aligned}$$
(14)

with \( m_{\text {max}}^{}\) being the largest eigenvalue of the neutrino mass matrix,

$$\begin{aligned} m_\nu ^{}=U{\hat{m}}_\nu ^{} U^T_{} = U \text {diag}\{m_1^{}, m_2^{}, m_3^{}\} U^T_{}. \end{aligned}$$
(15)

Here the PMNS matrix U contains three mixing angles, one Dirac phase and two Majorana phases, i.e.

$$\begin{aligned} U= & {} \left[ \!\!\begin{array}{ccl} \!\!c_{12}^{}c_{13}^{}&{} \!\!s_{12}^{}c_{13}^{}&{}\!\! s_{13}^{}e^{-i\delta }_{}\\ \!\!-\!s_{12}^{}c_{23}^{}\!-\!c_{12}^{}s_{23}^{}s_{13}^{}e^{i\delta }_{} &{}\!\!~~c_{12}^{}c_{23}^{}\!-\!s_{12}^{}s_{23}^{}s_{13}^{}e^{i\delta }_{} &{}\!\! s_{23}^{}c_{13}^{}\\ \!\! ~~s_{12}^{}s_{23}^{}\!-\!c_{12}^{}c_{23}^{}s_{13}^{}e^{i\delta }_{} &{} \!\!-\!c_{12}^{}s_{23}^{}\!-\!s_{12}^{}c_{23}^{}s_{13}^{}e^{i\delta }_{} &{} \!\!c_{23}^{}c_{13}^{} \end{array}\!\!\right] \nonumber \\&\times \text {diag}\{e^{i\alpha _1^{}/2}_{}, e^{i\alpha _2^{}/2}_{}, 1\}. \end{aligned}$$
(16)
Fig. 1
figure 1

The lepton-number-violating processes for generating the Majorana neutrino masses

Full size image

The linear seesaw can be also understood at the electroweak level. From the Yukawa interactions (7), we can read

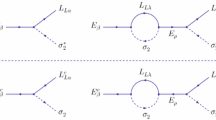
$$\begin{aligned}&{\mathcal {L}}\supset - {\hat{y}}_e^{}{\bar{l}}_L^{}{\tilde{\phi }}_L^{} e_R^{} - {\hat{M}}_E^{} {\bar{E}}_R^{c} E_L^{c} - X_R^{} {\hat{y}}_N^{} {\bar{l}}_L^{}\chi _L^{} N_L^{c} \nonumber \\&\quad -{\hat{M}}_N^{} {\bar{N}}_R^c N_L^c -y_L^{} X_R^{*} {\bar{l}}_L^{}\sigma _1^{} N_R^{}-y_L^{}{\bar{l}}_L^{}{\tilde{\sigma }}_2^{} E_R^{}+\text {H.c.}\,\nonumber \\&\quad \text {with}~y_N^{} = X_R^{} {\hat{y}}_N^{} X_L^\dagger ,~X_{L,R}^\dagger X_{L,R}^{}=X_{L,R}^{} X_{L,R}^\dagger =1.\nonumber \\ \end{aligned}$$
(17)

Here the yukawa couplings \(y_{e}^{}\) and the mass matrices \(M_{E,N}^{}\) have been chosen to be diagonal and real without loss of generality. As shown in Fig. 1, the left-handed neutrinos \(\nu _L^{}\) can acquire their Majorana masses (11) by integrating out the heavy Dirac pairs \(N=N_L^{}+N_R^{}\), i.e.

$$\begin{aligned}&{\mathcal {L}}\supset -\frac{1}{2}y_L^{} X_R^{*} \frac{1}{{\hat{M}}_{N}^{}} {\hat{y}}_N^{} X_R^T {\bar{l}}_L^{}\sigma _{1}^{} \chi _L^{T} l_L^c \nonumber \\&\qquad - \frac{1}{2}X_R^{} {\hat{y}}_N^{} \frac{1}{{\hat{M}}_{N}^{}} X_R^\dagger y_L^T {\bar{l}}_L^{}\chi _L^{}\sigma _{1}^{T} l_L^c +\text {H.c.}\nonumber \\&\quad = - \frac{1}{2}\frac{y_L^{}}{\langle \chi _R^0\rangle } \left( {\bar{l}}_L^{}\sigma _{1}^{} \chi _L^{T} l_L^c + {\bar{l}}_L^{}\chi _L^{}\sigma _{1}^{T} l_L^c \right) +\text {H.c.}. \end{aligned}$$
(18)

Note from the linear seesaw (11),

$$\begin{aligned} m_\nu ^{}=-2 y_L^{} \langle \sigma _1^{0} \rangle \frac{ \langle \chi _L^{0} \rangle }{ \langle \chi _R^{0} \rangle }=-y_L^{}\frac{\mu _2^2}{{\hat{M}}_N^{}}{\hat{y}}_N^{}, \end{aligned}$$
(19)

the conditions \(y_{N,L}^{}< \sqrt{4\pi }\), \(\mu _2^{2}<2.79\times 10^{4}_{}\,\text {GeV}^2_{}\) and \(m_{\text {max}}^{}\ge 0.05\,\text {eV}\) should put an upper bound on the heavy Dirac fermion masses,

$$\begin{aligned} M_N^{}<7\times 10^{15}_{}\,\text {GeV}. \end{aligned}$$
(20)

4 Lepton and baryon asymmetries

As shown in Fig. 2, the mirror charged leptons \(E_\beta ^{}\) can decay into the ordinary lepton doublets \(l_{L\alpha }^{}\) and the Higgs doublet \(\sigma _2^{}\). These decays can generate three individual lepton asymmetries \(L_{e,\mu ,\tau }^{}\) stored in the ordinary lepton flavors \(l_{Le,L\mu ,L\tau }^{}\) if the CP is not conserved, i.e.

$$\begin{aligned} L_{\beta \alpha }^{}\propto & {} \Gamma (E_\beta ^{}\rightarrow L_{L\alpha }^{}\sigma _2^{})-\Gamma (E_\beta ^{c}\rightarrow L_{L\alpha }^{c}\sigma _2^{*})\ne 0\,,\nonumber \\ L_\alpha ^{}= & {} \sum _{\beta }^{}L_{\beta \alpha }^{}. \end{aligned}$$
(21)

We calculate the decay width at tree level,

$$\begin{aligned} \Gamma _\beta ^{}\equiv & {} \Gamma (E_\beta ^{}\rightarrow l_{L\alpha }^{} +\sigma _2^{})=\Gamma (E_\beta ^{c}\rightarrow l_{L\alpha }^{c} +\sigma _2^{*})\nonumber \\= & {} \frac{1}{16\pi } \left( y_L^\dagger y_L^{}\right) _{\beta \beta }^{} M_{E_\beta }^{}\nonumber \\= & {} \frac{1}{16\pi } \frac{\left( m_\nu ^\dagger m_\nu ^{}\right) _{\beta \beta }^{}}{\mu _1^2} M_{E_\beta }^{}, \end{aligned}$$
(22)

and then the CP asymmetry at one-loop level,

$$\begin{aligned} \varepsilon _{\beta \alpha }^{}= & {} \frac{\Gamma (E_\beta ^{}\rightarrow l_{L\alpha }^{} +\sigma _2^{})-\Gamma (E_\beta ^{c}\rightarrow l_{L\alpha }^{c} +\sigma _2^{*})}{\Gamma _\beta ^{} }\nonumber \\= & {} \frac{1}{4\pi }\sum _{\rho }^{}\frac{\text {Im}\left[ \left( y_L^\dagger y_L^{}\right) _{\rho \beta }^{} y_{L\alpha \beta }^{*} y_{L\alpha \rho }^{} \right] }{\left( y_L^\dagger y_L^{}\right) _{\beta \beta }^{}}\frac{M_{E_\beta }^2 }{M_{E_\beta }^2-M_{E_\rho }^2 }\nonumber \\= & {} \frac{1}{4\pi }\sum _{\rho }^{}\frac{\text {Im}\left[ \left( m_\nu ^\dagger m_\nu ^{}\right) _{\rho \beta }^{} m_{\alpha \beta }^{*} m_{\alpha \rho }^{} \right] }{ \mu _1^2 \left( m_\nu ^\dagger m_\nu ^{}\right) _{\beta \beta }^{}}\frac{m_{\beta }^2 }{m_{\beta }^2-m_{\rho }^2 }. \end{aligned}$$
(23)

It is easy to check

$$\begin{aligned} \varepsilon _{\beta e}^{}+ \varepsilon _{\beta \mu }^{}+ \varepsilon _{\beta \tau }^{}\equiv 0, \end{aligned}$$
(24)

as a result of the lepton number conservation.

The decays of the mirror electron-positron pairs should dominate the individual lepton asymmetries \(L_{e,\mu ,\tau }^{}\) since the mirror electron is much lighter than the mirror muon and tau. Actually, the out-of-equilibrium decays of the mirror muons and taus in principle could also produce the individual lepton asymmetries \(L_{e,\mu ,\tau }^{}\). However, at that moment the Yukawa interactions involving the mirror electrons were still in equilibrium so that they would wash out the produced individual lepton asymmetries \(L_{e,\mu ,\tau }^{}\) from the mirror muon and tau decays. When the mirror electrons and positrons go out of equilibrium at a temperature \(T_D^{}\), the individual lepton asymmetries \(L_{e,\mu ,\tau }^{}\) can be produced, i.e.

$$\begin{aligned} L_\alpha ^{} \simeq \left. \varepsilon _{e\alpha }^{}\left( \frac{n_{E_e}^{}}{s}\right) \right| _{T=T_D^{}}^{}. \end{aligned}$$
(25)

Here \(n_{E_e}^{}\) is the number density and s is the entropy density. For the following demonstration, we specify the decay width,

$$\begin{aligned} \Gamma _{e}^{}= & {} \frac{1}{16\pi } \frac{\left( m_\nu ^\dagger m_\nu ^{}\right) _{ee}^{}}{\mu _1^2} M_{E_e}^{}, \end{aligned}$$
(26)

and the CP asymmetries,

$$\begin{aligned} \varepsilon _{ee}^{}\simeq & {} -\frac{1}{4\pi }\frac{\text {Im}\left[ \left( m_\nu ^\dagger m_\nu ^{}\right) _{\mu e}^{} m_{e e}^{*} m_{e \mu }^{} \right] }{ \mu _1^2 \left( m_\nu ^\dagger m_\nu ^{}\right) _{ee}^{}}\frac{m_{e}^2 }{m_{\mu }^2},\nonumber \\ \varepsilon _{e\mu }^{}\simeq & {} -\frac{1}{4\pi }\frac{\text {Im}\left[ \left( m_\nu ^\dagger m_\nu ^{}\right) _{\mu e}^{} m_{\mu e}^{*} m_{\mu \mu }^{} \right] }{ \mu _1^2 \left( m_\nu ^\dagger m_\nu ^{}\right) _{ee}^{}}\frac{m_{e}^2 }{m_{\mu }^2},\nonumber \\ \varepsilon _{e\tau }^{}\simeq & {} -\frac{1}{4\pi }\frac{\text {Im}\left[ \left( m_\nu ^\dagger m_\nu ^{}\right) _{\mu e}^{} m_{\tau e}^{*} m_{\tau \mu }^{} \right] }{ \mu _1^2 \left( m_\nu ^\dagger m_\nu ^{}\right) _{ee}^{}}\frac{m_{e}^2 }{m_{\mu }^2}. \end{aligned}$$
(27)
Fig. 2
figure 2

The lepton-number-conserving decays of the mirror charged leptons into the ordinary leptons

Full size image

On the other hand, the model provides the lepton-number-violating interactions for generating the Majorana neutrino masses, as shown in Fig. 1. The interaction rates of the related lepton-number-violating processes such as \(l_{L\alpha }^{}l_{L\beta }^{} \rightarrow \chi _L^{}\sigma _1^{}\) are computed by [46]

$$\begin{aligned} \Gamma _{\alpha \beta ^{}}^{}=\frac{1}{\pi ^3_{}} \frac{\left| m_{\alpha \beta }^{}\right| ^2_{} T^3_{}}{v^4_{}}~~\text {for}~~T<M_N^{}. \end{aligned}$$
(28)

At the temperature,

$$\begin{aligned} T_{\alpha \beta }^{}= & {} \left( \frac{8\pi ^{9}_{}g_{*}^{}}{90} \right) ^{\!\frac{1}{2}}_{}\frac{v^4_{}}{M_{\text {Pl}}^{}\left| m_{\alpha \beta }^{}\right| ^2_{} } \nonumber \\= & {} 1.63\times 10^{13}_{}\,\text {GeV}\left( \frac{0.05\,\text {eV}}{\left| m_{\alpha \beta }^{}\right| }\right) ^2_{}, \end{aligned}$$
(29)

these lepton-number-violating processes will begin to decouple, i.e.

$$\begin{aligned} \left. \left[ \Gamma _{\alpha \beta ^{}}^{}< H(T)=\left( \frac{8\pi ^{3}_{}g_{*}^{}}{90}\right) ^{\frac{1}{2}}_{} \frac{T^2_{}}{M_{\text {Pl}}^{}}\right] \right| _{T<T_{\alpha \beta }^{}}^{}. \end{aligned}$$
(30)

Here H(T) is the Hubble constant with \(M_{\text {Pl}}^{}\simeq 1.22\times 10^{19}_{}\,\text {GeV}\) being the Planck mass and \(g_{*}^{}=110.75\) being the relativistic degrees of freedom (the SM fields plus one additional Higgs doublet \(\sigma _{2}^{}\)).

If all of the above lepton-number-violating processes such as \(l_{L\alpha }^{}l_{L\beta }^{} \rightarrow \chi _L^{}\sigma _1^{}\) keep in equilibrium during the mirror electron decays, the individual lepton asymmetries \(L_{e,\mu ,\tau }^{}\) can not be produced at all. Instead, they would be washed out once they were produced. However, we can require that the lepton-number-violating processes such as \(l_{L\alpha }^{}l_{L\beta }^{} \rightarrow \chi _L^{}\sigma _1^{}\) have no effects on the lepton flavor \(l_{L\gamma \ne \alpha ,\beta }^{}\). In consequence, the mirror electron decays can still contribute a lepton asymmetry \(L_{\gamma \ne \alpha ,\beta }^{}\). This means we can expect the lepton asymmetry stored in certain lepton flavor(s) to survive from the lepton-number-violating processes, i.e.

$$\begin{aligned} L=\left\{ \begin{array}{lll}L_e^{}&{}\text {for}&{}T_{\mu \mu ,\mu \tau , \tau \tau }^{}<T_D^{}<T_{ee,e\mu ,e\tau }^{}\,,\\ L_\mu ^{}&{}\text {for}&{}T_{ee,e\tau ,\tau \tau }^{}<T_D^{}<T_{e\mu ,\mu \mu ,\mu \tau }^{},\\ L_\tau ^{}&{}\text {for}&{}T_{ee,e\mu ,\mu \mu }^{}<T_D^{}<T_{e\tau ,\mu \tau ,\tau \tau }^{},\\ L_e^{}+L_\mu ^{}&{}\text {for}&{}T_{\tau \tau }^{}<T_D^{}<T_{ee,e\mu ,e\tau ,\mu \mu ,\mu \tau }^{},\\ L_e^{}+L_\tau ^{}&{}\text {for}&{}T_{\mu \mu }^{}<T_D^{}<T_{ee,e\mu , e\tau ,\mu \tau ,\tau \tau }^{},\\ L_\mu ^{}+L_\tau ^{}&{}\text {for}&{}T_{ee}^{}<T_D^{}<T_{e\mu ,e\tau , \mu \mu ,\mu \tau ,\tau \tau }^{}.\end{array}\right. \end{aligned}$$
(31)

Here we have assumed the heavy Dirac fermions \(N=N_L+N_R\) much heavier than the crucial temperature \(T_D^{}\). The \(SU(2)_L^{}\) sphaleron processes then can partially transfer the remnant lepton asymmetry L to a baryon asymmetry B. From Eq. (29), the lepton-number-violating processes can go out of equilibrium before the sphalerons become active, i.e.

$$\begin{aligned} T_{\alpha \beta }^{}> T_{\text {sph}}^{}\simeq 10^{12}_{}\,\text {GeV}. \end{aligned}$$
(32)

The final baryon asymmetry B then can be given by [47]

$$\begin{aligned} B= -\frac{28}{79} L. \end{aligned}$$
(33)

We would like to emphasize that both the production and the washout of the individual lepton asymmetries \(L_{e,\mu ,\tau }^{}\) take place above the temperatures \(T>T_{\text {sph}}^{}\simeq 10^{12}_{}\,\text {GeV}\), at which the Yukawa interactions between the SM left- and right-handed leptons have not been in equilibrium yet. So, the flavor effect in the usual leptogenesis scenario [15, 24] will not appear in the above demonstrations. Instead, the remnant lepton asymmetry L in Eq. (31) can be treated as a single-flavor lepton asymmetry when it participates in the sphaleron processes [15, 24].

5 Numerical example

To give a numerical estimation, we consider the weak washout region [48], i,e,

$$\begin{aligned} K=\frac{\Gamma _e^{}}{2H}\left| _{T=M_{E_e}^{}}^{}\right. \ll 1. \end{aligned}$$
(34)

Accordingly, when the mirror electrons and positrons finally decay [48],

$$\begin{aligned} T_D^{} \sim M_{E_e}^{}\sqrt{K}, \end{aligned}$$
(35)

they are very overabundant: \(n_{E_e^{}} \sim n_{\gamma }^{} \), i.e. no exponential suppression in their number density. Here \(n_\gamma ^{}\) is the number density of photons. We hence can expect Eq. (25) to be [48]

$$\begin{aligned} L_\alpha ^{}\simeq \left. \varepsilon _{e\alpha }^{}\left( \frac{n_{E_e}^{}}{s}\right) \right| _{T=T_D^{}}^{} \sim \varepsilon _{e\alpha } \left( \frac{n_\gamma ^{}}{s}\right) \sim \frac{\varepsilon _{e\alpha }}{g_*^{}}. \end{aligned}$$
(36)

In this case, as shown in Eqs. (26), (27), (29), (31), (33), (34), (35) and (36), the final baryon asymmetry can be fully determined by the charged lepton masses, the Majorana neutrino mass matrix and the parameters \(\mu _{1,2}^{}\) and \(M_{E_e}^{}\).

We have known the charged lepton masses \(m_e^{}=511\,\text {keV}\), \(m_\mu ^{}=107\,\text {MeV}\), and the normal(inverted) neutrino parameters \(\Delta m_{21}^2=m_2^2-m_1^2=7.37\times 10^{-5}_{}\,\text {eV}^2_{}\), \(\Delta m_{31}^2(\Delta m_{23}^2)=m_3^2- m_1^2(m_2^2-m_3^2)=2.56(2.54)\times 10^{-3}_{}\,\text {eV}^2_{}\), \(\sin ^2_{}\theta _{12}^{}=0.297\), \(\sin ^2_{}\theta _{23}^{}=0.425 (0.589)\), \(\sin ^2_{}\theta _{13}^{}=0.0215 (0.0216)\) [1]. It seems difficult for the inverted hierarchical and quasi-degenerate neutrinos to fulfil the conditions in Eq. (31). So, we consider the normal hierarchical neutrinos to give a numerical estimation. As an example, we fix \(m_1^{}=0\), \(\alpha _2^{}=\pi /2\), \(\delta =3\pi /2\), and then take \(\mu _1^{}=0.21\,\text {eV}\), \(\mu _2^2= 2.79\times 10^{4}_{}\,\text {GeV}^2_{}\), \(M_{E_e}^{}=3\times 10^{16}_{}\,\text {GeV}\). With these inputs, we obtain \(K\simeq 1.9\times 10^{-5}_{}\), \(\varepsilon _{ee}^{}\simeq -3.4\times 10^{-8}_{} \), \(T_D^{}\sim 1.3\times 10^{14}_{}\,\text {GeV}\), \(T_{\tau \tau }^{}\simeq 4.3\times 10^{13}_{}\,\text {GeV}\), \(T_{\mu \tau }^{}\simeq 8.1\times 10^{13}_{}\,\text {GeV}\), \(T_{\mu \mu }^{}\simeq 7.5\times 10^{13}_{}\,\text {GeV}\), \(T_{e\mu }^{}\simeq 7.7\times 10^{14}_{}\,\text {GeV}\), \(T_{e\tau }^{}\simeq 2.1\times 10^{15}_{}\,\text {GeV}\), \(T_{ee}^{}\simeq 1.1\times 10^{16}_{}\,\text {GeV}\) and hence \(B \sim 10^{-10}_{}\).

6 Conclusion

In this paper we have demonstrated a novel linear seesaw scenario for paramerizing the cosmic baryon asymmetry by the charged lepton masses, the light Majorana neutrino mass matrix and the heavy mirror charged lepton masses. Through the lepton-number-conserving decays of the mirror electron-positron pairs, we can obtain three individual lepton asymmetries stored in the ordinary lepton flavors although the total lepton asymmetry is exactly zero. The lepton-number-violating processes for the neutrino mass generation can wash out the lepton asymmetry stored in certain ordinary lepton flavor(s). Remarkably, these lepton-number-conserving and lepton-number-violating interactions originate from the same Yukawa couplings. The remnant lepton asymmetry can be partially converted to a baryon asymmetry by the sphaleron processes. Our scenario seems difficult to work for an inverted hierarchical or a quasi-degenerate neutrino spectrum. Instead, it prefers to the normal hierarchical neutrino spectrum which is hinted by the present data from neutrino oscillations and cosmological observations [1].