Abstract
The modeling of multiple parton interactions in Monte Carlo event generators is a crucial part not only for the dressing of signal processes but also to describe data with a minimum bias on the event selection. Much work has and will be put into the theoretical framework and the numerical implementation of these models. In this contribution, we document various improvements of the multiple parton interaction model of Herwig 7 (Bellm et al. in Eur Phys J C76(4):196, 2016), that lead to an improved description of minimum bias and underlying event data.
Similar content being viewed by others
1 Introduction and motivation
Due to the composite nature of hadrons, it is possible to have multiple parton interactions (MPI) during a single scattering event. The nature of these interactions is responsible for the various final state topologies which are being measured at hadronic collisions. Final states with an accumulation of several particles with high transverse momentum (\(p_{\perp }\)) are typically referred to as jets and can be described reliably with the methods of perturbative QCD. On the other hand, when no high \(p_{\perp }\) particles are present, the event is usually characterized by large hadronic activity, distributed flat in rapidity with a relatively low \(p_{\perp }\). These events are attributed to the soft regime where the methods of perturbative QCD break down and one has to rely on modelling. This distinction in hard and soft events is of course not always clear. Especially in the transition region between hard and soft interactions, the correct interplay of the models becomes crucial. For a full description of the experimental data available, diffractive events need to be incorporated into the simulation chain as well. Multi purpose event generators like Herwig [1, 2], Sherpa [3] and Pythia [4, 5], all have models that simulate this part of the hadronic interactions [6,7,8,9,10,11,12,13]. The model for hard MPI was introduced in the newer C++ Version of Herwig in Refs. [9, 10] and extended to the soft regime in Ref. [14]. The additional soft and hard interactions are seamlessly integrated into the existing framework and lie at the intersection between the parton shower of the hard process and the hadronization model. The soft interactions have been revised in Ref. [15] and replaced with a parton ladder obeying multiperipheral kinematics [16, 17]. The combination with the newly introduced model for diffraction led to an improved description of the majority of Minimum Bias (MB) and Underlying Event (UE) observables [15]. Recently, and already including various of the changes described in this contribution, information on the space–time structure of MPIs and colour reconnection was introduced in Ref. [18]. In this paper, we give a detailed description of the various changes to the MPI model in Herwig 7 [1, 2] that have accumulated over the past months and resulted in an improved description of various UE and MB observables.
The paper is structured as follows. In Sect. 2 we review the current state of the multi parton interaction model in Herwig, with a focus on the event generation workflow and the technicalities of the simulation. In Sect. 3 we summarize the modifications to the MPI model. After describing the tuning procedure in Sect. 4, we show the impact of the modifications and compare to data in Sect. 5.
2 Current state
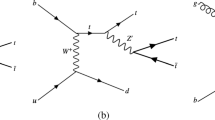
Pictorial representation of the processes contributing to the modelling of minimum bias production in Herwig. On the left-hand side the ‘dummy’ process to start hard (QCD two-to-two process) and soft (quark pair with gluon ladder) multiple parton interactions. On the right the two possible single and double diffraction processes. If no hard scatter is produced the incoming beams are modelled without colour exchange
For a detailed description of the theoretical basis of the MPI model, we refer to [19]. In the following, we give an overview of the different building blocks of the simulation in order to put multiple parton interactions in the right context. As it stands, the MPI framework in Herwig is split into two parts: First, the non-diffractive part (ND), with a hard interaction that breaks up both protons of the incoming state and requires at least one additional scatter. Second, the diffractive part that keeps either one of the incoming protons intact [single diffraction (SD)] or breaks both protons [double-diffraction (DD)] without colour exchange.
The starting point of the simulation is a hard process, which, by construction, is forced to evolve back to a valence quark. This introduces forced splittings where the possible forced splittings are performed based on probabilities calculated from DGLAP splitting kernels. Once this is performed the number of additional soft and hard scatters is determined [19]. The additional hard scatters constructed from regular QCD two-to-two processes are – including shower and backwards evolution to gluons – attached to the beam remnant. If the showering process or possible forced splitting to gluons creates states that are not compatible with the already extracted energy fraction, the additional scatter is discarded and a new trial is performed. Once the hard additional scatters are added, the RemnantHandler of Herwig adds the additional soft scatters to the process. It is possible to choose between the traditional soft two-to-two processes or the multiperipheral model introduced in Ref. [15]. We will concentrate on the model described in Ref. [15] as it solved long-standing issues in the description of rapidity gap observables reported in Ref. [20]. The multiperipheral model [15] makes use of the same transverse momentum distribution as the traditional two-to-two soft model but creates gluon ladders that are distributed equidistantly in rapidity placed between a quark–antiquark pair. At this point, the ladders are located as color singlets randomly between the current beam remnants. To ensure momentum conservation the simplistic choice has been made to correlate the gluons pairwise. As a consequence of this, unphysical correlation observables can be constructed to identify this feature. Once the additional soft and hard scatters are attached to the event and beam remnant the hadronization and color reconnection models take over. The second component, namely the diffractive events are constructed using the MEDiffraction Matrix element of Herwig. A detailed description of kinematics and particle production is given in Ref. [15]. For the understanding of the following paragraphs, only the overall normalization of the diffractive cross-section is of relevance as hardly any changes have been made to the modeling.
It is furthermore possible to simulate ND events without the requirement to have a specific hard process (like e.g. higgs production). In this case the hard process is replaced with a dummy process which extracts an quark or an antiquark from the proton without transverse momentum or parton showering. This process is governed by the MEMinBias matrix element. In the current state, the MEMinBias is weighted with a parameter called CSNorm. Additionally the diffractive cross-sections come with factors that can be modified to stir the amount of SD and DD events. In order to reproduce the overall cross section correctly a cross-section reweigther, PostProcessReweighter, was introduced to ensure that the sum of SD, DD, and ND add up to the inelastic cross-section.
To illustrate the various components of the MinBias production mechanisms Fig. 1 shows from left to right the dummy process that comes with hard (QCD two-to-two like) and soft (quark pair with gluon-ladder) non-diffractive processes as well as the SD and DD processes.
3 Modifications
In this section, we describe modifications to the existing algorithms, starting with changes that are supposed to keep the result unmodified but improve the ability to produce events. We then focus on changes that will modify the physics in a motivated manner.
3.1 Reweighting
Before Herwig 7.2, a PostProcess-Reweighter was introduced to modify the event weights such that the cross-section calculated in the MPIHandler restores the inelastic cross-section. In this construction, events with variable weights, that can even be negative, were produced. To circumvent this behaviour, we modified the matrix elements. They now keep track of their cross-section and reweight the next events such that the desired cross-section is produced on the hard cross-section level. The net effect is that the reweighting is pulled to the stage before unweighting such that the produced and further evolved events have unit weights. This makes the event generation more efficient and improves the performance with respect to event generator tuning as well.
For the reweighting we solve,
for w, where \(\sigma _{D}\) is the desired, \(\sigma _{C} \) is the current cross-section and the pair N and \(\varDelta \) are the current number of points and the weight updating interval respectively, we choose \(\varDelta =50\). The cross-section without reweigthing \(\sigma _{\mathrm {no rew.}}\) is, for large number of points N,
where \(\bar{w} \) is the average weight calculated as \(\sum w / N\).
The change improves the performance of the cross-section calculation and furthermore, has an impact on the tail of the \({\mathrm {d}}N/{\mathrm {d}}N_{\mathrm {ch}}\) observable from Ref. [21]. In Fig. 2 we show the effect of the new on-the-fly reweighting method compared to the PostProcessReweighter on the \({\mathrm {d}}N/{\mathrm {d}}N_{\mathrm {ch}}\) observable. We compare the two different reweighting methods by making 100 runs with 50k events for each reweighting method and plot the N value divided by the respective average value \(\langle N\rangle \) in the respective bin \(N_{\mathrm {ch}}\). We see that the new reweighting method leads to less variation and fewer outliers compared to the old reweighting method. We note that the applied reweighting procedure will not induce any unwanted event-by-event correlations in the limit of a sufficient number of events for a reliable computation of observables.
Comparison between the two reweighting methods with respect to the \({\mathrm {d}}N/{\mathrm {d}}N_{\mathrm {ch}}\) observable of Ref. [21]. Each line corresponds to a run with 50k events. The new reweighting method produces less outliers and has less variance than the old reweighting method
3.2 DiffractionRatio
To vary the ratio between non-diffractive and diffractive events the parameter CSNorm in the matrix element to produce the non-diffractive cross-section was used. We change this behaviour and introduce a parameter that gives the fraction of diffractive cross-section with respect to the non-diffractive cross-section, named the DiffractionRatio. As the cross-section of the dummy process was constructed such that scale and cuts on the incoming momenta fraction can influence the unphysical – that is reweighted to the physical – cross-section it is beneficial to parametrize the influential quantity, to begin with. The cross-section of hard and soft MPIs that are used in the eikonal model is now adjusted such that the sum, after eikonalisation gives the total cross-section. As in this model, the diffractive part is seen to be included in the two components, the DiffractionRatio now takes out a part of the non-elastic cross-section after eikonalisation.
3.3 Partner and scale choice
The shower starting conditions are a delicate problem and especially in the case of hard MPIs it is possible to enhance or reduce the amount of additional radiation. Further, the recoil of possible emissions and the kinematic reconstruction can be modified in various schemes that will not modify the accuracy of the showering process. In earlier versions, it was argued that the color partner of a radiating parton should be chosen such that the angle is maximal and the scale of the emitter is chosen with respect to the partner parton. We modify this to a scheme that chooses the evolution partner of the gluons randomly and then, as before, choosing the scale with respect to this chosen partner. This scheme is already the standard when using NLO corrections or external LHE-files for event generation in Herwig. In Sect. 5 we also discuss the possibility of choosing the scale different from the evolution partner.
3.4 Dummy process using valence quarks
In the Herwig event generation for the description of MB data a hard dummy process was introduced to keep the default workflow and enable event generation with multiple hard subprocesses. The matrix element that was introduced to hardly alter the observed final state returns parton configurations that have zero transverse momentum and an energy fraction that is given by the parton distribution functions. We observed that the number of trials needed to generate the average number of hard MPIs \(\langle n_{\mathrm {hard}}\rangle \) strongly exceeds \(\langle n_{\mathrm {hard}} \rangle \). The reason for this can be found in the dummy events that are produced with sea quark content. Those events are, as the Herwig remnant will expect the primary hard process to end on a valence quark, forced to split back to a valence quark. As the leg(s) with sea-quark content will not perform a showering (zero \(p_t\)), it will need two forced splittings – first to a gluon and then to a valence quark – in order to be extracted from the remnant. This procedure takes a large portion of the energy of the proton, such that additional scatters, if they are required to be added, will be forced/biased to have smaller momentum fractions and therefore produce a softer final state. Requiring the (anti-)quarks to match the valence quark content of the (anti-)proton will modify the spectrum as can be seen in Fig. 6.
3.5 Kinematics of soft ladder
The parton kinematics in the soft ladder were generated following the algorithm presented in Ref. [17]. This approach led to highly anticorrelated mini-jet events as was pointed out in Ref. [22]. After initial studies in Ref. [23], this issue has been resolved with an improved algorithm based on the ideas in Ref. [24]. The number N of the partons in the soft ladder is drawn from a Poissonian distribution with mean
where \(N_{\mathrm {ladder}}\) and \(B_{\mathrm {ladder}}\) are parameters which will be tuned to MB and UE data, \(p_{r1,2}\) are the momenta of the incoming remnants and \(m_{\mathrm {rem}}\) is the constituent mass of the remnant. Instead of directly calculating the momentum fraction necessary to distribute the partons equally spaced in rapidity, we sample the rapidities of the partons flat in the available rapidity interval \(-Y_{\mathrm {max}}<y<Y_{\mathrm {max}}\) defined by the two beam remnants. This enhances the variance in the rapidity compared to the previous algorithm where the rapidity values essentially were pre-determined by the available energy in the beam remnant system. The effect of the new approach on the mini-jet events can be seen in Fig. 7.
3.6 Soft ladder transverse momentum
Another significant change to the model for soft interactions affects the transverse momentum distribution of the ladder partons. Instead of drawing the \(p_{\perp }\) of every parton in the ladder from the distribution
only one \(p_{\perp }\) of the soft ladder partons is sampled according to Eq. 3. The \(p_{\perp },2...n\) of the remaining partons have to fulfill the requirement that \(p_{\perp ,2..n}<p_{\perp ,1}\). This is necessary in order not to bias the resulting \(p_{\perp }\) distribution towards higher values and to reproduce the shape of the \(\mathrm {d} \sigma _{\mathrm {soft}}/\mathrm {d} p_{\perp }\) distribution as calculated within the eikonal model (see [19]). In Fig. 8 we show the resulting the \(\mathrm {d}\sigma _{\mathrm {soft}}/\mathrm {d}p_{\perp }\) distribution for the hardest parton in the ladder by comparing the new sampling with the old sampling and see that the shape of Eq. 3 is reproduced with the new sampling algorithm. Furthermore, the change in assigning the \(p_{\perp }\) values to the ladder partons leads to a significant improvement in the low multiplicity region of the \(\langle p_{\perp } \rangle ~\mathrm {vs.}~N_{\mathrm {ch}}\) observable as is shown in Fig. 9.
3.7 Modified power law for \(p_{\perp }^{\mathrm {min}}\)(s)
The power law for the energy extrapolation of the parameter \(p_{\perp }^{\mathrm {min}}\)(s) was found to describe data at high centre-of-mass energies. Incorporating lower centre-of-mass energies proved to be difficult since with the existing power-law, the eikonal model could not be solved in a consistent way. A dedicated tuning procedure led to a modified power-law including \(p_{\perp }^{\mathrm {min}}\)(s) values tuned to MB and UE data from centre-of-mass energies below 900 GeV. The modified power law for the \(p_{\perp }^{\mathrm {min}}\) parametrization now reads
where b is the offset necessary to fit the \(p_{\perp }^{\mathrm {min}}\) values for small \(\sqrt{s}\). A detailed description of the tuning procedure and the parametrization is outlined in Sect. 4.
3.8 Colour disrupt
Furthermore, several attempts were undertaken to incorporate different colour connection topologies similar to Ref. [25], in order to minimize the number of MPI events containing sizeable rapidity gaps \(\varDelta \eta \), mimicking diffractive processes. But none of the tested topologies involving a colour connection between the beam remnant and the parton ladder resulted in an improved description of data. We, therefore, stick to the current implementation which treats the parton ladder as a colour singlet and connects the beam remnant to the hard part of the event.Footnote 1
4 Tuning to MB and UE data
Since there were several changes to the underlying structure of the MPI model and the soft part of the MPI model itself, a retune of the model parameters is necessary. We tune the model to MB and UE data covering the centre-of-mass energy, \(\sqrt{s}\), between 200 GeV and 13 TeV. The tuning was performed by using the Rivet [26] and Professor [27] frameworks for Monte-Carlo event generators in combination with Autotunes [28]. The parameters considered in the tuning are the main parameters of the MPI model, the minimum transverse momentum \(p_{\perp }^{\mathrm {min}}\) and the inverse proton radius squared \(\mu ^2\), the parameters determining the number of partons in the soft ladder, \(N_{\mathrm {ladder}}\) and \(B_{\mathrm {ladder}}\) (see Eq. 2), the fraction of the diffractive cross-section from the inelastic cross-section \(R_{\mathrm {Diffraction}}\) and the two colour reconnection probabilities \(p_{\mathrm {Reco}}\), \(p_{\mathrm {RecoBaryonic}}\) of the modified colour reconnection model which was introduced in Ref. [29]. We start the tuning with a reassessment of the energy dependence of the minimum transverse momentum \(p_{\perp }^{\mathrm {min}}\) and the inverse proton radius squared \(\mu ^2\). The two parameters are the main parameters of the MPI model and are responsible for the interplay between hard and soft interactions by directly stirring the relevant cross-sections. We tune both values to MB and UE data from 200 GeV [30, 31], 500 GeV [31], 900 GeV [21, 32,33,34], 1.8 TeV [35,36,37,38,39], 7 TeV [20, 21, 32,33,34, 40, 41] and 13 TeV [42,43,44]. \(\mu ^2\) is not energy-dependent, which is reflected in the tunes for \(\sqrt{s}=7,13~{\mathrm {TeV}}\). For high centre-of-mass energies, the \(\chi ^2\) value also is less sensitive to the input from various combinations of Monte Carlo runs used for tuning. For smaller centre-of-mass energies, we note an increased sensitivity to the chosen runs. In a similar approach as in Ref. [45] we fix \(\mu ^2\) to the tightly constrained tuned values for 7 TeV and 13 TeV. Both favour small ranges of \(\mu ^2= 1.1\) but with different values for \(p_{\perp }^{\mathrm {min}}\) independent of the run combinations used for tuning. With \(\mu ^2\) fixed we then re-tune \(p_{\perp }^{\mathrm {min}}\) to the different centre-of-masss energies. The median values for \(p_{\perp }^{\mathrm {min}}\) and the corresponding spread of the values and the ranges for \(\mu ^2\) resulting from the different run combinations are listed in Table 1. We note here that these values do not correspond to the best tune values which will result in the overall minimal value for \(\chi ^2\). Important at this stage is to find a sensible parametrization which approximately captures the energy dependence of the \(p_{\perp }^{\mathrm {min}}(s)\) parameter at different centre-of-mass energies.
In order to account for a good description of MB and UE data over the considered energy range between 200 GeV and 13 TeV it is necessary to modify the existing power law parametrization of the \(p_{\perp }^{\mathrm {min}}\) parameter [45] and introduce an energy offset to account for the \(p_{\perp }^{\mathrm {min}}\) values at \(\sqrt{s}<900\,{\mathrm {GeV}}\). The modified power law is given in Eq. 4. A plot with the tuned \(p_{\perp }^{\mathrm {min}}\) values and the resulting fit are shown in Fig. 3. We find that the \(p_{\perp }^{\mathrm {min}}\) points can be fitted with the parameter values summarized in Table 2 if we demand that the parametrization must reproduce the \(p_{\perp }^{\mathrm {min}}\)(s) values for \(\sqrt{s}=7,13\) TeV opting for an improved description at higher centre-of-mass energies taking into account a less optimal fit of \(p_{\perp }^{\mathrm {min}}(s)\) at \(\sqrt{s}=200\) GeV.
With the modified parametrization, the MPI model of Herwig works at all centre-of-mass energies considered and the reoccurring issue that the hard cross-section exceeds the total cross-section is no longer present for small \(\sqrt{s}\).
The remaining parameters of the MPI model (\(N_{\mathrm {ladder}}\), \(B_{\mathrm {ladder}}\), \(R_{\mathrm {Diffraction}}\)) and the two colour reconnection probabilities (\(p_{\mathrm {Reco}}\), \(p_{\mathrm {RecoBaryonic}}\)) are tuned to MB and UE data measured at the LHC at 7 TeV, and 13 TeV. We restrain from tuning to single observables and instead focus on an overall reduction of the total \(\chi ^2\) measure. The resulting set of parameters which were tuned with the new parametrization for the \(p_{\perp }^{\mathrm {min}}\)-values are listed in Table 3.
In addition to the energy-independent tune, we provide individual tunes for the full set of MPI parameters for 7 TeV and 13 TeV which were performed with the Autotunes framework for tuning [28]. The resulting parameter values are also listed in Table 4.
All performed parameter scans showed no dependence of the goodness of fit value on the \(B_{\mathrm {ladder}}\) parameter which we set to zero. The tuned value for the ladder multiplicity varies between 0.6 and 0.699 which can be seen as a sign for weak energy dependence and we conclude that Eq. 2 captures the energy dependence of the ladder multiplicity. The value of the diffractive ratio is mainly driven by the \({\mathrm {d}}\sigma /{\mathrm {d}}\varDelta \eta ^F\) observables from Refs. [20, 46] and the diffractive cross-sections measurements, \(\sigma _{\mathrm {SD}}\), \(\sigma _{\mathrm {DD}}\) from Ref. [47] at 7 TeV. More data at different \(\sqrt{s}\) is needed to correctly assess the energy dependence of the diffractive cross-section (see e.g. Ref. [48]). The high value for the reconnection probabilities is due to the requirement of the colour reconnection model that a certain rapidity configuration of quarks within clusters has to be met in order to be considered for reconnection. The effective reconnection probability is therefore lower. The probability for baryonic reconnection is mainly driven by flavour observables at 7 TeV. As can be seen in Table 4, \(p_{\mathrm {RecoBaryonic}}\) drops significantly from 7 TeV to 13 TeV. Nonetheless, it is possible to have more baryonic clusters due to the increased multiplicity at 13 TeV.
In Sect. 5 we show some exemplary plots where we compare Herwig 7.1.5 to the modified MPI model. The parameters presented in this paper are set as the default in the new release of Herwig 7.2 and can be used as a well-motivated baseline describing general properties of MB and UE data over a wide range of centre-of-mass energies.
The modified power-law parametrization of the energy dependence of the \(p_{\perp }^{\mathrm {min}}\) parameter with the given values is used as the default in the new Herwig release 7.2.
5 Results
In this paper, we have presented various changes to the MPI model in Herwig. With the mentioned modifications in Sect. 3 we see a good description of MB and UE observables combined across all considered centre-of-mass energies. In this section, we discuss the resulting influence of the modifications described in Sect. 3 on some handpicked observables. A complete set of all observables with the current model is available on the webpage [49].
Impact of the DiffractionRatio parameter choices in comparision to differential cross-section data measured in Ref. [50]
The charged-particle multiplicity is plotted against the rapidity for multiple cuts on the hardest track transverse momentum and number of charged particles. The data is taken from Ref. [33]. This observable is sensitive to the choices that are employed as the starting conditions of the parton shower process. The four choices are described in Sect. 3. Height differences are easily modified in the tuning process, but shape differences prefer choices with a random colour partner for gluons in the hard process
5.1 DiffractionRatio
The parameter gives an easier handle on the fraction of diffractive events and can be tuned to observables sensitive to diffractive events like the rapidity gap cross-section \({\mathrm {d}}\sigma /{\mathrm {d}}\varDelta \eta ^F\) as measured by CMS and ATLAS at 7 TeV. In Fig. 4 we show the \({\mathrm {d}}\sigma /{\mathrm {d}}\varDelta \eta ^F\) observable for three different values of the DiffractionRatio parameter. We see that varying the DiffractionRatio modifies the differential cross-section with respect to events containing large rapidity gaps \(\varDelta \eta ^F\) but leaves the region with \(\varDelta \eta ^F<2\) largely invariant which is dominated by non-diffractive particle production.
5.2 Partner and scale choice
The impact of the partner and scale choice is shown in Fig. 5. In comparison to data from Ref. [33] showing the charged multiplicity as a function of rapidity in MB events, we give results from the four choices implemented in Herwig. We note, that in the tuning process the height can be modified by multiple variables, like the value of the strong coupling or the ladder multiplicity. The shape of the distributions, however, depends more on the underlying dynamics and in this case the shower evolution. The best reproduction of the central plateau at \(p_{\perp }\ge 500\) MeV leading tracks and the dip for low energy leading tracks can be achieved by choosing the evolution partner of the gluon randomly between one of the two colour connected partners.
We show the model comparison to normalized cross-section data from Ref. [33] as a function of the number of charged particles in the event. The figure depicts the influence of the possibility of extracting only valence quarks (blue) or all light flavours (red) at the stage of the ’dummy’ process. It further shows the possibility of multiple trials n in the generation of additional scatters
5.3 Dummy process using valence quarks
Figure 6 shows the impact of choosing all light quark flavours to be initial states to the dummy process starting the generation of soft and/or hard additional scatters. Further, we allow each additional scatter to be reproduced n times if the showering of the additional hard process ends up in a momentum configuration that is not supported by the current energy fractions extracted from either of the protons. It is visible that depending on the choice a change of up to 50% in the tails of the charged particle multiplicities can be generated. As can be expected, allowing multiple tries to regenerate configurations contributes to higher particle multiplicities. Further, the restriction to “only valence” quark extraction and the reduction of forced splittings also contributed to an increased charged particle multiplicity as on average with higher energy additional scatters are possible. This figure also illustrates the possible variation one should expect from such subtle changes.
5.4 Kinematics of soft ladder
The plot from Ref. [22] with the new kinematic description is shown in Fig. 7. The new kinematics is necessary to account for more fluctuations in the rapidity values for the produced partons in the soft ladder and removes the unphysical anticorrelation seen in Ref. [22] for \(\eta \approx -2\). The change to the kinematic description does not necessarily result in a better description of data but was necessary for a physically more sound model (Fig. 8).
Comparison between Herwig 7.1.5 and the improved version of the model. Plot of the minijet correlations from Ref. [22]
Transverse momentum distribution of the hardest parton in the ladder and the parametrization according to Eq. 3. With the new sampling method, the bias towards larger \(p_{\perp }\) values disappears and the parametrization is reproduced
Comparison between the old and the improved version of the model. The plot shows the average transverse momentum \(\langle p_{\perp }\rangle \) against the charged particle multiplicity \(N_{\mathrm {ch}}\) observable as measured by ATLAS [33]
5.5 Soft ladder transverse momentum
The change in the sampling of the transverse momentum of the partons produced during soft interactions is best shown with the \(\langle p_{\perp }\rangle \) vs. \(N_{\mathrm {ch}}\) observable. although the description seems to worsen in the high \(N_{\mathrm {ch}}\) tail the majority of the events has multiplicities of up to 100 charged particles. With the new assignment of \(p_{\perp }\) the bump for \(N_{\mathrm {ch}}<40\), which was present in the old version disappears since we notably shift the \(p_{\perp }\) of the produced particles towards lower values which is in alignment with the measurements in that multiplicity region. The resulting plot is shown in Fig. 9. For the \(N_{\mathrm {ch}}>100\) region, we produce too many soft particles. A detailed study concentrating on high multiplicity events would be needed to remedy that problem.
6 Conclusion and outlook
In this paper, we have summarized various changes to the MPI model in Herwig. We have introduced a parameter called DiffractiveRatio which gives an easy handle on the fraction of diffractive events in a collision. We have reviewed and changed the model for soft interactions with a well-motivated change to the \(p_{\perp }\) distribution of the partons produced in a soft ladder. To achieve a better description of data we changed the partner and scale setting for gluons in the starting conditions of the angular ordered parton shower. Furthermore, we tuned the modified model to MB and UE data covering an energy range between 200 GeV and 13 TeV which led to a modification of the existing energy extrapolation of the MPI model. The resulting tune gives generally a good description of all observables with only one set of parameters, albeit due to the nature of the combined tune, there are some aspects which are not described satisfactorily.
Especially in the high multiplicity region, we fail to describe the data correctly for observables like \(\langle p_{\perp }\rangle \) vs. \(N_{\mathrm {ch}}\).
With the rising number of differential measurements at the LHC, especially flavour observables and measurements probing the high multiplicity region of hadronic collisions, it becomes harder for multi-purpose Monte Carlo event generators to capture all phenomena observed in the measurements and to account for a sensible description of data. In this paper, we have taken the approach to tune the free parameters of the MPI model to as many observables as possible where the only guidance was the overall \(\chi ^2\) value.
The modifications described in this paper are a step towards a better understanding of soft and non-perturbative physics at high energy colliders. Next steps are needed. The inclusion of the diffractive cross-section in the eikonal model has been improved but a full eikonalisation and the implications to the generation details of then possible multiple diffractive processes has not been addressed in this work. Furthermore, to correctly assess the energy dependence of the diffractive cross-section, more data at 13 TeV is needed.
The dummy process to start the generation of multiple scatters is a non-necessary construction that perhaps needs to be overcome at some point. Also the full connection with the work done in [18] and a rethinking of the colour connections of the soft ladders according to new measures, i.e. minimal masses, may be introduced.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The experimental data is publicly available as Rivet analyses, associated to the correspondingly cited experimental analyses. The simulation code is publicly available from https://herwig.hepforge.org and the plots and data files generated in the production of this paper can be found at https://herwig.hepforge.org/plots/herwig7.2/index.html.]
Notes
Correlations in the final state are introduced via colour reconnection.
References
J. Bellm et al., Herwig 7.0/Herwig++ 3.0 release note. Eur. Phys. J. C 76(4), 196 (2016) arXiv:1512.01178
J. Bellm et al., Herwig 7.1 Release Note. arXiv:1705.06919
E. Bothmann et al., Event generation with Sherpa 2.2. Sci. Post Phys. 7(3), 034 (2019). arXiv:1905.09127
T. Sjostrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006). arxiv:hep-ph/0603175
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten, S. Mrenna, S. Prestel, C.O. Rasmussen, P.Z. Skands, An Introduction to PYTHIA 8.2. arXiv:1410.3012
T. Sjöstrand, Multiple Parton–Parton interactions in hadronic events, in Proceedings, 23RD International Conference on High Energy Physics, July16–23, 1986 (Berkeley CA, 1985)
T. Sjöstrand, M. van Zijl, A multiple interaction model for the event structure in Hadron collisions. Phys. Rev. D 36, 2019 (1987)
T. Sjöstrand, P.Z. Skands, Multiple interactions and the structure of beam remnants. JHEP 03, 053 (2004). arxiv:hep-ph/0402078
M. Bähr, J.M. Butterworth, M.H. Seymour, The underlying event and the total cross section from tevatron to the LHC. JHEP 01, 065 (2009). arXiv:0806.2949
M. Bähr, S. Gieseke, M.H. Seymour, Simulation of multiple partonic interactions in Herwig++. JHEP 07, 076 (2008). arXiv:0803.3633
R. Corke, T. Sjöstrand, Multiparton interactions and rescattering. JHEP 01, 035 (2009). arXiv:0911.1909
R. Corke, T. Sjöstrand, Multiparton interactions with an x-dependent proton size. JHEP 05, 009 (2011). arXiv:1101.5953
A. Martin, H. Hoeth, V. Khoze, F. Krauss, M. Ryskin et al., Diffractive physics. PoS QNP 2012, 017 (2012). arXiv:1206.2124
M. Bähr, J.M. Butterworth, S. Gieseke, M.H. Seymour, Soft interactions in Herwig++. arXiv:0905.4671
S. Gieseke, P. Kirchgaeßer, F. Loshaj, Soft and diffractive scattering with the cluster model in Herwig. Eur. Phys. J. C 77(3), 156 (2017). arXiv:1612.04701
D. Amati, S. Fubini, A. Stanghellini, Theory of high—energy scattering and multiple production, in High-Energy Physics. Proceedings, 11th International Conference, ICHEP’62, Geneva, Switzerland, Jul 4–11, 1962 (1962), pp. 560–564
M. Baker, K.A. Ter-Martirosian, Gribov’s Reggeon calculus: its physical basis and implications. Phys. Rep. 28, 1–143 (1976)
J. Bellm, C.B. Duncan, S. Gieseke, M. Myska, A. Siódmok, Spacetime colour reconnection in Herwig 7. arXiv:1909.08850
M. Bähr et al., Herwig++ physics and manual. Eur. Phys. J. C 58, 639–707 (2008). arXiv:0803.0883
ATLAS Collaboration Collaboration, G. Aad et al., Rapidity gap cross sections measured with the ATLAS detector in \(pp\) collisions at \(\sqrt{s}=7\) TeV, Eur.Phys.J. C72, 1926 (2012) arXiv:1201.2808
ALICE Collaboration, K. Aamodt et al., Charged-particle multiplicity measurement in proton–proton collisions at \(\sqrt{s}=7\) TeV with ALICE at LHC. Eur. Phys. J. C68, 345–354 (2010). arXiv:1004.3514
M. Azarkin, P. Kotko, A. Siodmok, M. Strikman, Studying minijets and MPI with rapidity correlations. Eur. Phys. J. C 79(3), 180 (2019). arXiv:1806.09016
S. Gay, Hadronisation in herwig 7, Master’s thesis, KIT (2018)
S. Jadach, Rapidity generator for Monte-Carlo calculations of cylindrical phase space. Comput. Phys. Commun. 9(5), 297–304 (1975)
S. Gieseke, F. Loshaj, M. Myska, Towards Diffraction in Herwig. in Proceedings, 7th International Workshop on Multiple Partonic Interactions at the LHC (MPI@LHC 2015): Miramare, Trieste, Italy, November 23-27, 2015 (2016), pp. 53–57. arXiv:1602.04690
A. Buckley, J. Butterworth, L. Lönnblad, D. Grellscheid, H. Hoeth et al., Rivet user manual. Comput. Phys. Commun. 184, 2803–2819 (2013). arXiv:1003.0694
A. Buckley, H. Hoeth, H. Lacker, H. Schulz, J.E. von Seggern, Systematic event generator tuning for the LHC. Eur. Phys. J. C 65, 331–357 (2010). arXiv:0907.2973
J. Bellm, L. Gellersen, High dimensional parameter tuning for event generators. arXiv:1908.10811
S. Gieseke, P. Kirchgaeßer, S. Plätzer, Baryon production from cluster hadronisation. Eur. Phys. J. C 78(2), 99 (2018). arXiv:1710.10906
STAR Collaboration, B.I. Abelev et al., Systematic measurements of identified particle spectra in \(p p, d^+\) Au and Au+Au collisions from STAR. Phys. Rev. C 79, 034909 (2009). arXiv:0808.2041
UA1 Collaboration, C. Albajar et al., A study of the general characteristics of \(p\bar{p}\) collisions at \(\sqrt{s}\) = 0.2-TeV to 0.9-TeV. Nucl. Phys. B335, 261–287 (1990)
ATLAS Collaboration, G. Aad et al., Measurement of underlying event characteristics using charged particles in pp collisions at \(\sqrt{s} = 900 GeV\) and 7 TeV with the ATLAS detector. Phys. Rev. D83, 112001 (2011). arXiv:1012.0791
ATLAS Collaboration, G. Aad et al., Charged-particle multiplicities in pp interactions measured with the ATLAS detector at the LHC. New J. Phys. 13, 053033 (2011). arXiv:1012.5104
ATLAS Collaboration, G. Aad et al., Measurements of underlying-event properties using neutral and charged particles in \(pp\) collisions at 900 GeV and 7 TeV with the ATLAS detector at the LHC. Eur. Phys. J. C71, 1636 (2011). arXiv:1103.1816
CDF Collaboration, F. Abe et al., Transverse momentum distributions of charged particles produced in \(\bar{p}p\) interactions at \(\sqrt{s} = 630\) GeV and 1800 GeV. Phys. Rev. Lett. 61, 1819 (1988)
CDF Collaboration, F. Abe et al., Pseudorapidity distributions of charged particles produced in \(\bar{p}p\) interactions at \(\sqrt{s} = 630\) GeV and 1800 GeV. Phys. Rev. D 41, 2330 (1990). [119(1989)]
CDF Collaboration, D. Acosta et al., Soft and hard interactions in \(p\bar{p}\) collisions at \(\sqrt{s}=\) 1800-GeV and 630-GeV. Phys. Rev. D 65, 072005 (2002)
CDF Collaboration, T. Affolder et al., Charged jet evolution and the underlying event in proton-antiproton collisions at 1.8 TeV. Phys. Rev. D65, 092002 (2002)
CDF Collaboration, D.E. Acosta et al., Underlying event in hard interactions at the Fermilab Tevatron \(\bar{p}p\) collider. Phys. Rev. D 70, 072002 (2004). (hep-ex/0404004)
ALICE Collaboration, J. Adam et al., Measurement of pion, kaon and proton production in proton–proton collisions at \(\sqrt{s} = 7\) TeV. Eur. Phys. J. C 75(5), 226 (2015). arXiv:1504.00024
CMS Collaboration, V. Khachatryan et al., Strange particle production in \(pp\) collisions at \(\sqrt{s}=0.9\) and 7 TeV. JHEP 05, 064 (2011). arXiv:1102.4282
ATLAS Collaboration, M. Aaboud et al., Measurement of charged-particle distributions sensitive to the underlying event in \( \sqrt{s}=13 \) TeV proton-proton collisions with the ATLAS detector at the LHC. JHEP 03, 157 (2017). arXiv:1701.05390
ATLAS Collaboration, M. Aaboud et al., Charged-particle distributions at low transverse momentum in \(\sqrt{s} = 13\) TeV \(pp\) interactions measured with the ATLAS detector at the LHC. Eur. Phys. J. C 76(9), 502 (2016). arXiv:1606.01133
CMS Collaboration, A. M. Sirunyan et al., Measurement of charged particle spectra in minimum-bias events from proton–proton collisions at \(\sqrt{s}=13\,\text{TeV} \). Eur. Phys. J. C 78(9), 697 (2018). arXiv:1806.11245
S. Gieseke, C. Röhr, A. Siódmok, Colour reconnections in Herwig++. Eur. Phys. J. C 72, 2225 (2012). arXiv:1206.0041
CMS Collaboration, S. Chatrchyan et al., Measurement of differential cross sections for the production of a pair of isolated photons in pp collisions at \(\sqrt{s}=7\,\text{ TeV } \). Eur. Phys. J. C 74(11), 3129 (2014). arXiv:1405.7225
ALICE Collaboration, B. Abelev et al., Measurement of inelastic, single- and double-diffraction cross sections in proton–proton collisions at the LHC with ALICE. Eur. Phys. J. C 73(6), 2456 (2013). arXiv:1208.4968
C.O. Rasmussen, T. Sjöstrand, Models for total, elastic and diffractive cross sections. Eur. Phys. J. C 78(6), 461 (2018). arXiv:1804.10373
Herwig. https://herwig.hepforge.org/. Accessed 15 May 2020
CMS Collaboration, V. Khachatryan et al., Measurement of diffraction dissociation cross sections in pp collisions at \(\sqrt{s}\) = 7 TeV. Phys. Rev. D92(1), 012003 (2015). arXiv:1503.08689
Acknowledgements
We would like to thank the Herwig collaboration and especially Cody B. Duncan, Miroslav Myska, Andrzej Siódmok and Peter Richardson for valuable discussions on the topic. We thank Steffen Gay for his contributions in the early stages of this work. This work was supported by the MCnetITN3 H2020 Marie Curie Initial Training Network under Grant agreement 722104. This project has also received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, Grant agreement No. 668679. This work has been supported by the BMBF under Grant number 05H18VKCC1
Author information
Authors and Affiliations
Corresponding author
A Parameter values
A Parameter values
In this appendix, we present the tuned parameter sets discussed in Sect. 4. Note that the parameter set of Table 3 will become the default in the next Herwig release 7.2 and the parameters in Table 4 are dedicated tunes to 7 TeV and 13 TeV LHC data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Bellm, J., Gieseke, S. & Kirchgaeßer, P. Improving the description of multiple interactions in Herwig. Eur. Phys. J. C 80, 469 (2020). https://doi.org/10.1140/epjc/s10052-020-8002-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-8002-y