1 Introduction

Wormholes are throat-like geometrical structures which connect two parallel universes or otherwise distant parts of the same universe. In 1988, Morris and Thorne presented a family of traversable wormholes [1, 2], where the fundamental ingredient is the flaring-out condition of the wormhole throat. This condition leads to violation of the null energy condition (NEC) in the framework of general relativity (GR). Matter that violates NEC is denoted by exotic matter [3, 4]. Then, One of the most important challenges in wormhole scenarios is the establishment of standard energy conditions. Several avenues of research have been explored in order to minimize the usage of exotic matter [5]. For instance, Visser and Poisson have studied the construction of thin-shell wormholes where the supporting matter is concentrated on the wormhole’s throat [6]. Thin-shell wormholes extensively investigated in the literature [7,8,9,10,11,12,13,14,15,16]. Also, a large amount of work has been devoted to build and study wormhole solutions within the framework of modified gravity theories among which we quote: wormhole solutions in Brans–Dicke theory [17,18,19,20], f(R) gravity [21,22,23], Born-Infeld theory [24, 25], third order Lovelock theory [26], Kaluza–Klein gravity [27, 28], scalar-tensor gravity [29] and solutions in the presence of a cosmological constant have been reported in [30, 31]. Recently, the possibility of existence of traversable wormholes in the context of f(R, T) gravity have been reported in the literature, such as wormhole formation with two types of varying Chaplygin gas [32], wormhole solutions satisfying the energy conditions in the exponential f(R, T) gravity [33], see also [34,35,36,37,38] for other solutions in this theory.

Though in GR framework, static wormhole configurations require fluid sources that violate the NEC, there are nonstatic Lorentzian wormholes without the need of WEC violating matter to sustain them. Such wormhole structures can live for arbitrarily small or large time intervals [39, 40] or even satisfy the dominant energy condition (DEC) in the whole spacetime [41]. Work along this line has been extended towards dynamical wormhole geometries which satisfy the energy conditions and the averaged energy conditions over timelike or null geodesics during a time period [42, 43]. An interesting scenario is that the expansion of the Universe could increase the size of the static wormholes by a factor which is proportional to the scale factor of the Universe, in a time-dependent inflationary background [44]. Evolving wormholes in a cosmological background have been studied in [42, 45,46,47,48,49,50,51,52], and dynamic wormhole spacetimes supported by two fluids and also by a polytropic equation of state (EoS) have been investigated in [53, 54] and [55], respectively. It is noteworthy that in modified gravity it is possible to obtain wormhole solutions by imposing that normal matter satisfies the energy conditions. This possibility is due to the presence of additional ingredients, not present in GR, that could sustain wormhole geometries without the need of exotic matter. Such configurations that respect energy conditions throughout the spacetime have been reported in the framework of Einstein–Cartan gravity [56, 57]. An alternative way to obtain traversable wormhole configurations satisfying WEC or at least minimum violation of it, is to consider modified matter sources see e.g., [58, 59] and references therein. However, generalizing the matter sector may not necessarily guarantee to obtain a setting for non-exotic wormhole geometries [60,61,62].

In recent years, there has been considerable interest in the subject of higher curvature gravity, much of which has been motivated through attempts to provide a quantum description of the gravitational field. The Einstein–Hilbert action with higher curvature interactions can lead to a renormalizable theory of gravity [63]. In the low energy limit of string theory, the Gauss–Bonnet term and a linear combination of the Lovelock terms will add to Einstein–Hilbert action [64, 65]. More recently, higher curvature gravity has been of interest in holography [66, 67] and has been considered in the context of cosmology [68, 69]. Bhawal and Kar studied N-dimensional Lorentzian wormholes in Einstein–Gauss–Bonnet gravity [70]. These solutions with normal and exotic matter which are limited to the vicinity of the throat was also explored. Explicit wormhole solutions respecting energy conditions in the whole spacetime were obtained in vacuum and dust cases with \(k=-1\), where k is the sectional curvature of an \( (n - 2)\) symmetric space [71]. However, these solutions were further extended to the positive \(k=1\) sectional curvature and for the first time specific solutions that satisfy the WEC throughout the spacetime were found in [72]. In the context of third-order Lovelock gravity it was shown that one may impose the matter threading the wormhole to satisfy the energy conditions, so that it is the higher order curvature terms that sustain these exotic geometries [73]. Also, dynamic wormhole solutions in this framework with compact extra dimensions were analyzed in [74].

The present paper investigates expanding wormholes in higher dimensions that is an important ingredient of the modern theories of fundamental physics, such as Kaluza–Klein, string theory and supergravity [75,76,77,78,79,80,81]. It is shown that higher-dimensional evolving wormholes can be obtained satisfying NEC throughout spacetime [82]. However, in four dimensions, the solutions satisfy the NEC in specific time intervals. In this work, we are motivated to find dynamical solutions in Gauss–Bonnet gravity that satisfy the energy conditions throughout the spacetime utilizing a homogeneous Ricci scalar as presented in standard cosmological models. This paper is organized as follows: in Sect. 2, we present a brief review on (n+1)dimensional field equations of Gauss–Bonnet gravity. In Sect. 3, we obtain wormhole solutions in different expansionary regimes and examine the validity of WEC in detail. Our conclusions are drawn in Sect. 4.

2 Action and field equations

The action in the framework of GB theory is given by

$$\begin{aligned} I_{G}=\int d^{n}x\sqrt{-g}\left[ {\mathcal {R}}+\alpha _{2}{\mathcal {L}}_{GB} \right] , \end{aligned}$$
(1)

where n is the dimension of the space-time and \( \alpha _{2}\) is the Gauss–Bonnet (GB) coefficient. Also, \({\mathcal {R}}\) is the n -dimensional Ricci scalar and the GB term \({\mathcal {L}}_{GB}\) is given by

$$\begin{aligned} {\mathcal {L}}_{GB}={\mathcal {R}}^2-4{\mathcal {R}}_{\mu \nu }{\mathcal {R}}^{\mu \nu }+{\mathcal {R}}_{\mu \nu \rho \sigma }{\mathcal {R}}^{\mu \nu \rho \sigma }. \end{aligned}$$
(2)

In Lovelock theory, for each Euler density of order \({\bar{k}}\) in n dimensional space-time, only terms with \({\bar{k}}<n\) contribute to the equations of motion [84]. Therefore, the allowed solutions of the Einstein–Gauss–Bonnet theory are derived in \(n\ge 5\) dimensions. Note that the action (1) is recovered in the low energy limit of string theory [85,86,87,88].

Now, varying the action (1) with respect to metric, one obtains the field equations

$$\begin{aligned} G_{\mu \nu }+\alpha _{2}{\mathcal {G}}_{\mu \nu }=T_{\mu \nu }, \end{aligned}$$
(3)

where \(T_{\mu \nu }\) is the energy–momentum (EM) tensor, \(G_{\mu \nu }\) is the Einstein tensor and \({\mathcal {G}}_{\mu \nu }\) is the GB tensor, given by

$$\begin{aligned} {\mathcal {G}}_{\mu \nu }= & {} 2(-{\mathcal {R}}_{\mu \sigma \kappa \tau }{\mathcal {R}}_{{\nu }}^{\kappa \tau \sigma }-2{\mathcal {R}}_{\mu \rho \nu \sigma }{\mathcal {R}}^{\rho \sigma } \nonumber \\&-\,2{\mathcal {R}}_{\mu \sigma }{\mathcal {R}}_{\nu }^{\sigma }+{\mathcal {R}}{\mathcal {R}}_{\mu \nu })-\frac{1 }{2}{\mathcal {L}}_{GB}g_{\mu \nu }. \end{aligned}$$
(4)

We use a unit system with \(8\pi G_n=1\), where \(G_n\) is the n-dimensional gravitational constant.

In this work, we consider the n-dimensional traversable wormholes spacetime, by replacing the two-sphere [1, 2] with a \((n-2)\)-sphere ( \(d\Omega _{n-2}^{2}\) is the metric on the surface of the \((n-2)\) -sphere), given by the following line element

$$\begin{aligned} ds^{2}=-e^{2\phi (r)}dt^{2}+ R\left( t\right) ^2\left[ \frac{dr^{2}}{1-b(r)/r} +r^{2}d\Omega _{n-2}^{2}\right] \,, \end{aligned}$$
(5)

where R(t) is the scale factor of the universe, \(\phi (r)\) being the redshift function as it is related to the gravitational redshift and b(r) is the wormhole shape function. The shape function must satisfy the flare-out condition at the throat, i.e., we must have \(b^{\prime }(r_0)<1\) and \(b(r)<r\) for \(r>r_0\) in the whole spacetime, where \(r_0\) is the throat radius. The condition \(\phi (r)=0\) has been discussed in [89,90,91,92] that zero tidal force wormholes are supported by anisotropic fluid with a diagonal EM tensor. Our aim here is to study evolving wormholes with anisotropic pressures in an inhomogeneous spacetime which merge smoothly to the homogeneous FRW model. In the present work, we consider \(\phi (r)=0\) in order to ensure the absence of horizons and singularities throughout the spacetime. These evolving Lorentzian wormholes are conformally related to another family of static wormholes with zero-tidal force. The general constraints on these functions have been discussed by Morris and Thorne in [1, 2]. It is clear that if b(r) and \(\phi (r)\) tends to zero the metric (5) becomes the flat FRW metric, and as \(R(t) \rightarrow const\) the static Morris–Thorne wormhole is recovered. In the herein model, we search a way to determine the shape function b(r) and the scale factor R(t) in order to construct dynamical wormholes.

In an orthonormal reference frame, the nonzero components of the stress-energy tensor read

$$\begin{aligned} {T}^{\,\,\mu }_{\nu }={\mathrm{diag}}\left[ -\rho \left( r,t\right) ,P_{r}\left( r,t\right) ,P_{t}\left( r,t\right) ,P_{t}\left( r,t\right) ,\ldots \right] , \end{aligned}$$
(6)

where \(\rho \left( r,t\right) \) is the energy density and \(P_{r}\left( r,t\right) \) and \(P_{t}\left( r,t\right) \) are the radial and transverse pressures, respectively. Thus, the gravitational field equation (3) provides the components of \({T}^{\,\,\mu }_{\nu }\) as

$$\begin{aligned} \rho (r,t)= & {} {\frac{ \left( \left( n-1 \right) R ^{2} {H}^{2}+ \left( n-3 \right) Q +2\,p \right) \left( n- 2 \right) }{ 2 R^{2}}} \nonumber \\&+{\frac{\alpha \, \left( Q + H^{2} R^{2} \right) \left( n-2 \right) \left( \left( n-1 \right) R^{2} H ^{2 }+ \left( n-5 \right) Q +4\,p \right) }{2 R ^{4}}}, \end{aligned}$$
(7)
$$\begin{aligned} P_{r}\left( r,t\right)= & {} -{\frac{ \left( 2\, {\dot{H}} R ^{2}+ \left( n-1 \right) R ^{2} H ^{2}+ \left( n-3 \right) Q \right) \left( n-2 \right) }{2 R ^{2}}}\nonumber \\&-{\frac{ \left( 4\, {\dot{H}} R^{2}+ \left( n-1 \right) R^{2} H^{2}+ \left( n-5 \right) Q \right) \left( n-2 \right) \alpha \, \left( Q + H^{2} R^{2 } \right) }{ 2R^{4}}}, \end{aligned}$$
(8)
$$\begin{aligned} P_{t}\left( r,t\right)= & {} {\frac{-2\, R ^{2} \left( n-2 \right) {\dot{H}} - H^{2} \left( n-1 \right) \left( n-2 \right) R ^{2}- \left( \left( n-4 \right) Q +2\,p\right) \left( n-3 \right) }{2 R^{2}}}\nonumber \\&+\frac{\alpha \left( -4\,{R}^{2} \left( \left( n-2 \right) {H^{2}}{R}^{2}+ \left( n-4 \right) Q+2\,p \right) {\dot{H}} -H ^{4} \left( n -1 \right) \left( n-2 \right) {R}^{4}\right) }{2R^{4}} \nonumber \\&+\frac{\alpha (-2\, \left( \left( n-4 \right) Q+2\,p \right) {H}^{2} \left( n-3 \right) {R}^{2}- \left( \left( n-6 \right) Q+4\,p \right) Q \left( n-5 \right) )}{2R^{4}}, \end{aligned}$$
(9)

where an overdot denotes a derivative with respect to time. We define \(\alpha =(n-3)(n-4)\alpha _{2}\) and \(H=\frac{{\dot{R}}(t)}{R(t)}\) for notational convenience and the functions p and Q are given by

$$\begin{aligned} p={\frac{b^{\prime } r-b}{2{r}^{3}}},\quad Q=\frac{b}{r^3}. \end{aligned}$$
(10)

One can check that for \(R(t)=constant\), equations (7)–(9) reduce to the field equations as derived in the paper by Bhawal and Kar [70]. It is also easy to check that, for \(\alpha =0\) the field equations are those of higher-dimensional evolving wormholes in Einstein gravity [82].

3 Wormhole solutions

3.1 Energy–momentum conditions

It is well-known that static traversable wormholes in four dimensions violate energy conditions [93] which is due to the fulfillment of flaring-out condition near the throat of the wormhole. However, the energy conditions can be satisfied in the vicinity of static wormhole throats in higher-dimensional alternative theories of gravity [94,95,96,97] and the whole spacetime in the case of higher-order curvature terms [98]. On the other hand, evolving wormholes may avoid the energy condition violation for a limited time period. For the sake of physical reasonability of wormhole configuration the weak energy condition (WEC) must be satisfied. This condition requires that \(T_{\mu \nu }U^{\mu }U^{\nu }\ge 0\) , where \(U^{\mu }\) is a timelike vector. For a diagonal EM tensor, the WEC leads to the following inequalities

$$\begin{aligned} \rho \ge 0 , \quad \rho +P_{r} \ge 0,\quad || \rho +P_{t}\ge 0. \end{aligned}$$
(11)

Note that the last two inequalities are defined as the null energy condition (NEC). Using Eqs. (7)–(9), one finds the following relationships

$$\begin{aligned} \rho +P_{r}= & {} {\frac{ \left( p- {\dot{H}} {R} ^{2} \right) \left( n-2 \right) }{{R}^{2}}} -{\frac{ 2\alpha \left( {\dot{H}} {R}^{2}-p \right) \left( n-2 \right) \left( Q+ H ^{2}{R}^{2} \right) }{{R}^{4}}}, \end{aligned}$$
(12)
$$\begin{aligned} \rho +P_{t}= & {} {\frac{-{R}^{2} \left( n-2 \right) {\dot{H}} + \left( n-3 \right) Q+p}{{R}^{2}}}+\frac{2\alpha \left( \left( -5+n \right) Q+3\,p \right) Q}{R^4}\nonumber \\&+{\frac{2\alpha \, \left( -{R}^{2} \left( H ^{2} \left( n-2 \right) {R}^{2}+ \left( n-4 \right) Q+2\,p \right) {\dot{H}} + \left( \left( n-3 \right) Q+p \right) H^{2}{R}^{2} \right) }{{R}^{4}}}, \end{aligned}$$
(13)

where a prime and an overdot stand for differentiation with respect to r and t, respectively. From (12) we get at the throat

$$\begin{aligned} \left( \rho + P_r \right) \big |_{r=r_0}= & {} - \left( n-2 \right) \left( {\frac{1-b^{\prime }_0}{2{R}^{2}{{{ r}}_{\textit{0}}}^{2}}}+{\dot{H}} \right) \nonumber \\&\times \,\left( 1+2\,\alpha \,{H}^{2}+{\frac{2\alpha }{{{{ r}}_{\textit{0}}}^{2}{R}^{2}}}\right) . \end{aligned}$$
(14)

which shows that for \(\alpha =0\) and \(H=constant\) the NEC, and consequently the WEC, are violated at the throat, due to the flaring-out condition. In order to satisfy \(\rho + P_r >0\) in GB gravity, one can choose suitable values of H and \(\alpha \) at the wormhole throat.

3.2 Cosmological wormholes

We now have three equations, namely, the field equations (7)–(9), with the five unknown functions \(\rho (r,t),P_r(r,t),P_t(r,t),b(r)\) and R(t). Therefore, in order to determine the wormhole geometry, one can adopt several strategies [99,100,101]. Here, we are interested to study evolving wormholes with anisotropic pressures in an inhomogeneous spacetime which merge smoothly to the cosmological background. The wormhole solutions presented in a cosmological background have the interesting property that their Ricci scalar is independent of the radial coordinate r similar to what happens in cosmological settings [102, 103]. In other words, the scalar curvature of the spacetime is a function of time, only. The Ricci scalar corresponding to the metric (5) will play a fundamental role in our analysis which is obtained as

$$\begin{aligned} {\mathcal {R}}(t,r) = \left( n-1 \right) \left( n\, H^2+ 2\, {\dot{H}} \right) +{\frac{ \left( n-2 \right) \left( \left( n-3 \right) Q+2\,p \right) }{ R(t) ^{2}}}. \end{aligned}$$
(15)

It can be seen that the second term depends on r coordinate, hence in a cosmological background, condition \({\frac{\partial }{\partial r}}{{\mathcal {R}}} \left( t,r \right) =0 \) leads to the following differential equation

$$\begin{aligned} \left( n-3 \right) {\frac{d}{dr}}Q \left( r \right) +2\,{\frac{d}{dr}}p \left( r \right) =0. \end{aligned}$$
(16)

The above differential equation provides us with the following form for the shape function

$$\begin{aligned} b \left( r \right) ={{ C}_{\textit{1}}}\,{r}^{3}+{ C}_{\textit{2}}\,{r}^{-n+4}, \end{aligned}$$
(17)

where \( C_1\) and \( C_2\) are constants of integration. Notice that, the space slice \(t = const\) of the metric (5) for shape function introduced (with \(C_1=0\)) coincides with the space slice of the n-dimensional extension of the Schwarzschild black hole [104]. Using the condition \(b(r_0)=r_0\) at the throat we get

$$\begin{aligned} b(r)={{ C}_{\textit{1}}}\,{r}^{3}-{{{ r}}_{\textit{0}}}^{n-3} \left( {{ C}_{\textit{1}}}\,{{{ r}}_{\textit{0}}}^{2}-1 \right) {r}^{-n+4 }. \end{aligned}$$
(18)

Also the condition \(b^{\prime }(r_0) < 1\) leads to the following inequality

$$\begin{aligned} { C}_{\textit{1}}<{\frac{n-3}{{{{ r}}_{\textit{0}}}^{2} \left( n-1 \right) }}. \end{aligned}$$
(19)

We can now obtain constant \(C_1\) with using the fact that the space-time is asymptotically FRW along with applying the normalization \(C_1= 0, \pm 1\) for the curvature constant. It is clear that solutions with \(C_1= 0\) (flat universe) are asymptotically flat, i.e., \(\frac{b(r)}{r}\) tends to zero as \(r\rightarrow \infty \). Also, the condition \(b^{\prime }(r_0) < 1\) is satisfied for solution with \(C_1= -1\) (open universe). The case of wormhole solution with \(C_1= 1\) (closed universe) cannot be arbitrarily large.

With b(r) in hand, given by Eq. (18), and using the field equations (7)–(9), we obtain

$$\begin{aligned} \rho (r,t)= & {} \rho _{cb}(t) -{\frac{ \left( n-1 \right) \left( n-2 \right) \alpha \,{{ r}_{\textit{0}}}^{-4} \left( {{ C}_{\textit{1}}}\,{{{ r}}_{\textit{0}}}^{2}-1 \right) ^{2} }{2{R}^{4}}}\left( \frac{r_0}{r}\right) ^{2\,n-2}, \end{aligned}$$
(20)
$$\begin{aligned} P_{r}\left( r,t\right)= & {} P_{cb}(t) +{\frac{ \left( n-2 \right) r_0^{-2} \left( 2\,\alpha R ^{2}{\dot{H}} +\left( \alpha \,{H}^{2}+ 1/2 \right) \left( n-3 \right) {R}^{2}+\alpha \,{{ C}_{\textit{1}}}\, \left( n-5 \right) \right) \left( {{ C}_{\textit{1}}}\,{{ r0}}^{2}-1 \right) }{{R}^{4}}}\left( \frac{r_0}{r}\right) ^{\,n-1}\nonumber \\&-{\frac{\alpha \,\left( {{ C}_{\textit{1}}}\,{{ r0}}^ {2}-1 \right) ^{2} \left( n-5 \right) \left( n-2 \right) }{2{R}^{4}}}\left( \frac{r_0}{r}\right) ^{2\,n-2}, \end{aligned}$$
(21)
$$\begin{aligned} P_{t}\left( r,t\right)= & {} P_{cb}(t) -{\frac{ \left( 2\,\alpha R ^{2}{\dot{H}} +\left( \alpha \,{H}^{2}+1/2 \right) \left( n-3 \right) {R}^{2}+\alpha \,{{ C}_{\textit{1}}}\, \left( n-5\right) \right) \left( {{ C}_{\textit{1}}}\,{{ r0}}^{2}-1 \right) }{{R}^{4}}}\left( \frac{r_0}{r}\right) ^{\,n-1}\nonumber \\&+{\frac{n\,\alpha \, \left( {{ C}_{\textit{1}}}\,{{ r0}}^ {2}-1 \right) ^{2} \left( n-5 \right) }{2{R}^{4}}}\left( \frac{r_0}{r}\right) ^{2\,n-2}, \end{aligned}$$
(22)

where \(\rho _{cb}\) and \(P_{cb}\) components correspond cosmological background and are given by

$$\begin{aligned} \rho _{cb}(t)= & {} {\frac{ \left( n-2 \right) \left( {H}^{2}{R}^{2}+{{ C}_{\textit{1}}} \right) \left( \left( {H}^{2}{R}^{2}+{{ C}_{\textit{1}}} \right) \alpha +{R}^{2 } \right) \left( n-1 \right) }{2{R}^{4}}}, \end{aligned}$$
(23)
$$\begin{aligned} P_{cb}(t)= & {} -{\frac{ \left( \left( \left( 2+4\,\alpha \,H ^{2} \right) {R}^{4}+4\,\alpha \,{R}^{2}{} { C1} \right) {\dot{H}} + H ^{2} \left( 1+\alpha \,H ^{2} \right) \left( n-1 \right) {R}^{4} \right) \left( n-2 \right) }{2{R}^{4}}}\nonumber \\&-\frac{\left( \left( n-3 \right) { C1}\, \left( 1+2\alpha \,H ^{2} \right) {R}^{2}+\alpha \,{{ C1}}^{2} \left( n-5 \right) \right) \left( n-2 \right) }{2{R}^{4}}. \end{aligned}$$
(24)

Notice that for our solutions in a cosmological background, the components of \(\rho \), \(P_r\) and \(P_t\) are asymptotically independent of r. Moreover, their first terms depend only on time corresponding to a cosmological background as described by FRW spacetime. Let us now investigate the features of the evolving wormhole. We can determine the behavior of the scale factor by applying a linear equation of state between the radial pressure and energy density of the cosmological background profiles, i.e., \(P_{cb}=\omega \rho _{cb}\). We then obtain

$$\begin{aligned}&R^{2} \left( 2\, {\dot{H}} R ^{ 2}+ H ^{2} \left( w+1 \right) \left( n-1 \right) R ^{2}\nonumber \right. \\&\left. \quad + \left( \left( w+1 \right) n-w-3 \right) {{ C}_{\textit{1}}} \right) \nonumber \\&\quad +\alpha \,\left( {{ C}_{\textit{1}}}+ H ^{2} R^{2} \right) \left( 4\, {{\dot{H}}} R ^{ 2}+ H^{2} \left( w+1 \right) \left( n-1 \right) R^{2}\nonumber \right. \\&\left. \quad + \left( \left( w+1 \right) n-w-5 \right) {{ C}_{\textit{1}}} \right) =0. \end{aligned}$$
(25)

One can check that for \(\alpha =0\), the solution of Eq. (25) reduces to the scale factor for higher-dimensional GR [82]. In the following subsections, with the help of the master equation (25), we will determine the behavior of scale factor and the related properties of the energy conditions within the wormhole geometry in the presence of Gauss–Bonnet gravity. Thus, in order to study an evolving wormhole in detail, we consider three cases \(C_1=0\) and \(C_1=\pm 1\).

3.3 Solutions for the case \(C_1=0\)

We firstly solve the differential equation (25) to find the scale factor for GR case (\(\alpha =0\)) as

$$\begin{aligned} R \left( t \right) ={{ R}_ {\textit{1}}}\,{t}^{{\frac{2}{ \left( w+1 \right) \left( n-1 \right) }}}. \end{aligned}$$
(26)

In this case, one obtains the following expressions

$$\begin{aligned} \rho (r,t)= & {} {\frac{2\,n-4}{{t}^{2} \left( n-1 \right) \left( 1+w \right) ^{2}}}, \end{aligned}$$
(27)
$$\begin{aligned} \rho +P_r= & {} -\frac{(n-2)\left( {r}^{-n+1}{{{ r}}_{\textit{0}}}^{n} \left( n-1 \right) \left( n-3 \right) \left( 1+w \right) {t}^{{\frac{ \left( 2+2\,w \right) n-6-2\,w}{ \left( 1+w \right) \left( n-1 \right) }}}-4\,{{{ r}}_{\textit{0}}}^{3}{{ R}_{{\varvec{1}}}}^{2} \right) }{2\, \left( 1+w \right) \left( n-1 \right) {t}^{2}{{{ r}}_{\textit{0}}}^{3}{{ R}_{\textit{1}}}^{2} }, \end{aligned}$$
(28)
$$\begin{aligned} \rho +P_t= & {} \frac{{r}^{-n+1}{{{ r}}_{\textit{0}}}^{n} \left( n-1 \right) \left( n-3 \right) \left( 1+w \right) {t}^{{\frac{ \left( 2+2\,w \right) n-6-2\,w}{ \left( 1+w \right) \left( n-1 \right) }}}+4\,{{{ r}}_{\textit{0}}}^{3}{{ R}_{\textit{1}}}^{2} \left( n-2 \right) }{2\, \left( 1+w \right) \left( n-1 \right) {t}^{2}{{{ r}}_{\textit{0}}}^{3}{{ R}_{\textit{1}}}^{2}}. \end{aligned}$$
(29)

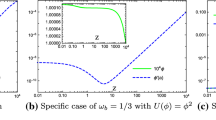
We see that for \(w>-1\) the values \(\rho \) and \(\rho +P_t\) are always positive, while the quantity \(\rho +P_r\) depends on the exponent of t, i.e, \(\frac{4}{ \left( 1+w \right) \left( n-1 \right) } \). So, for \(-{\frac{n-3}{n-1}}<w\) or \( {\frac{4}{ \left( 1+w \right) \left( n-1 \right) }}<2 \) at \(t=0\) the value of \(\rho +P_r\) is positive, while at large time it is negative. Moreover, we see that for \(w<-{\frac{n-3}{n-1}}\) at \(t=0\) the value of \(\rho +P_r\) is negative, while at large time it is positive. For \(w=-{\frac{n-3}{n-1}}\) with scale factor \(R(t)={ R}_{\textit{1}}\,t\) together with choosing suitable values of \({\frac{n-3}{{{ 2 R_1}}^{2}}}<r_0^2\) the WEC is satisfied (see Fig. 1).

Fig. 1
figure 1

The behavior of \(\rho +p_{r}\) with respect to r and t. The model parameters are chosen as \(w=-1/3\), \(R_1=2\) and \(r_0=1\) in 4 dimensions

Full size image
Fig. 2
figure 2

The behavior of \(\rho +p_{r}\) and \(\rho +p_{t}\) with respect to r and t. The model parameters are taken as \(\alpha =-0.5\), \(h=1\), \(R_2=1\) and \(r_0=1\) in 5-dimensions in the left and right plots, respectively

Full size image

Consider the inflationary expanding regime, i.e (\(w=-1\)), where by solving Eq. (25), we obtain the scale factor as \(R(t)=R_{2} e^{ht}\) and in order to check the WEC, we have

$$\begin{aligned} \rho (r,t)= & {} \frac{\left( n-2 \right) \left( n-1 \right) {h}^{2} \left( 1+\alpha \, {h}^{2} \right) }{2} \nonumber \\&-{\frac{\alpha \, \left( n-1 \right) \left( n-2 \right) }{2{{ R}_{\textit{2}}}^{4} r_0^{4}\left( {\mathrm{e}^{ht}} \right) ^{4}}}\left( \frac{r_0}{r}\right) ^{(2n-2)}, \end{aligned}$$
(30)
$$\begin{aligned} \rho +P_r= & {} -{\frac{ \left( n-2 \right) \left( n-3 \right) \left( 1+2\alpha \,{ h}^{2} \right) }{2{{ R}_{\textit{2}}}^{2} \left( {\mathrm{e}^{ht}} \right) ^{2}{{{ r}}_{\textit{0}}}^{2}}}\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \\&-{\frac{ \left( n-2 \right) \left( n-3 \right) \alpha \, }{{{ R2}}^{4} \left( {\mathrm{e}^{ht}} \right) ^{4}{{ r0}}^{4} }}\left( \frac{r_0}{r}\right) ^{(2n-2)}, \end{aligned}$$
(31)
$$\begin{aligned} \rho +P_t= & {} {\frac{\left( n-3 \right) \left( 1+2\alpha \,{h}^{2} \right) }{2{{ R}_{\textit{2}}}^{2} \left( {\mathrm{e}^{ht}} \right) ^{2}}}\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \\&-{\frac{\alpha \,\left( 1+n \right) }{{{ R}_{\textit{2}}}^{4} \left( {\mathrm{e}^{ht}} \right) ^ {4}{{{ r}}_{\textit{0}}}^{4} }}\left( \frac{r_0}{r}\right) ^{(2n-2)}. \end{aligned}$$
(32)

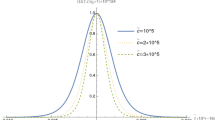
It is clear that both \(\rho +P_r\) and \(\rho +P_t\) tend to zero as \(t\rightarrow \infty \), with opposite signs. Therefore, in the limit of large times, one of the \(\rho +P_r\) or \(\rho +P_t\) quantities are negative and consequently the WEC is violated. However, we see that one can choose suitable value \(\alpha =-\frac{1}{2h^2}\) such that their first term is eliminated. For this case, the values of theses quantities are positive at the throat and at infinity. Figure 2 shows that it is possible to choose suitable values for the constants in order to satisfy the WEC in whole spacetime.

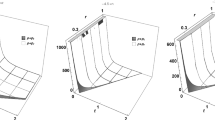
Finally, Since equation (25) cannot be solved analytically for R(t), we solve this equation numerically for a few values of the parameters \(\alpha \) and w and investigate the WEC. In Fig. 3 the scale factor versus time is plotted for \(\alpha =-1,0,1\) and \(w=-\frac{3}{4}\). Using then the field equations (7)–(9) for numerical values of the scale factor, we can plot the WEC. The numerical solutions are plotted in Fig. 4. These figures show that one can choose suitable parameters \(\alpha =1\),\(w=-\frac{3}{4}\) with \(r_0=2\) in five dimensions. Note that all of the quantities \(\rho \), \(\rho +P_r\) and \(\rho +P_t\) are positive at the throat and everywhere.

3.4 Solutions for the case \(C_1=-1\)

In this subsection, we study the open background, by using Eq. (25). We then find the analytical scale factor for \(w=-1\) as

$$\begin{aligned} R \left( t \right) ={{ R}_{\textit{3}}}\,\sinh \left( {\frac{t}{{{ R}_{\textit{3}}}}} \right) . \end{aligned}$$
(33)

In this case, we obtain the quantities \(\rho \), \(\rho +P_r\) and \(\rho +P_t\) as

$$\begin{aligned} \rho (r,t)= & {} \frac{ \left( n-1 \right) \left( n-2 \right) }{2{{{ R}_{\textit{3}}}}^{2}}\nonumber \\&+\alpha \,\left( {\frac{ \left( n-1 \right) \left( n-2 \right) }{2{{{ R}_{\textit{3}}}}^{4}} }\right. \nonumber \\&\left. -\frac{\left( n-1 \right) \left( {{ r}}_{\textit{0}}^{2}+1 \right) ^{2} \left( n-2 \right) }{2{{{ R}_{\textit{3}}}}^{4}{{ r0}}^{4}\left( \sinh \left( {\frac{t}{{{ R}_{\textit{3}}}}} \right) \right) ^{4} }\left( \frac{r_0}{r}\right) ^{2n-2} \right) , \end{aligned}$$
(34)
$$\begin{aligned} \rho +P_r= & {} -\frac{\left( {{{ r}}_{\textit{0}}}^{2}+1 \right) \left( n-2 \right) \left( n-3 \right) }{2\,{{{ r}}_{\textit{0}}}^{2}{{{ R}_{\textit{3}}}}^{2} \left( \sinh \left( {\frac{t}{{ R}_{\textit{3}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \\&+\alpha \,\left( -\frac{\left( {{{ r}}_{\textit{0}}}^{2}+1 \right) \left( n-2 \right) \left( n-3 \right) }{{{{ r}}_{\textit{0}}}^{2}{{{ R}_{\textit{3}}}}^{4} \left( \sinh \left( {\frac{t}{{{ R}_{\textit{3}}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \right. \\&\left. -\frac{\left( {{{ r}}_{\textit{0}}}^{2}+1 \right) ^{2} \left( n-2 \right) \left( n-3 \right) }{{{{ R}_{\textit{3}}}}^{4}{{{ r}}_{\textit{0}}}^{4} \left( \sinh \left( {\frac{t}{{{ R}_{\textit{3}}}}} \right) \right) ^{4} }\left( \frac{r_0}{r}\right) ^{2n-2}\right) , \end{aligned}$$
(35)
$$\begin{aligned} \rho +P_t= & {} \frac{\left( {{{ r}}_{\textit{0}}}^{2}+1 \right) \left( n-3 \right) }{2{{{ r}}_{\textit{0}}}^{2}{{{ R}_{\textit{3}}}}^{2} \left( \sinh \left( {\frac{t}{{{ R}_{\textit{3}}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1} \nonumber \\&+\alpha \,\left( \frac{\left( {{{ r}}_{\textit{0}}}^{2}+1 \right) \left( n-3 \right) }{{{{ r}}_{\textit{0}}}^{2}{{{ R}_{\textit{3}}}}^{4} \left( \sinh \left( {\frac{t}{{{ R}_{\textit{3}}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \right. \\&\left. -\frac{\left( {{{ r}}_{\textit{0}}}^{2}+1 \right) ^{2} \left( n+1 \right) }{{{{ R}_{\textit{3}}}}^{4}{{{ r}}_{\textit{0}}}^{4} \left( \sinh \left( {\frac{t}{{{ R}_{\textit{3}}}}} \right) \right) ^{4} }\left( \frac{r_0}{r}\right) ^{2n-2}\right) . \end{aligned}$$
(36)
Fig. 3
figure 3

The behavior of R(t) with respect to t for \(w=-3/4\), \(n=5\) and \(\alpha =-1,1,0\) from up to down, respectively

Full size image
Fig. 4
figure 4

The behavior of \(\rho \) , \(\rho +p_{t}\) and \(\rho +p_{r}\) with respect to t at throat \(r_0=2\) for the left figure and at \(r=5\) for the right figure from up to down, respectively. The constants are chosen as \(\alpha =1\), \(r_0=2\) and \(w=-3/4\) in 5-dimensions

Full size image

It is seen that in GR (\(\alpha =0\)), \(\rho +P_r\) is always negative, implying the violation of NEC throughout the spacetime. However, one can easily show that for \(t=0\) the WEC is satisfied by imposing the negative value \(\alpha \), due to the presence of the last term in Eqs. (35)–(36). We can also suitably choose the constants so that the WEC be satisfied in whole spacetime, Fig. 5.

3.5 Solutions for the case \(C_1=1\)

In the case of a close background, we can choose the wormhole throat such that the condition \(b^{\prime }(r_0) < 1\) is satisfied, i.e, \(r_0^2<\frac{n-3}{n-1}\). To be a solution of a wormhole, the condition \(0 < r- b(r)\) is also imposed. The condition \( b(r) = r\) leads to two real and positive roots given by \(r_{-} = r_0\) and \(r_{+}\) which satisfies the following equation

$$\begin{aligned} {r_{+}}^{n-1}-{r_{+}}^{n-3}-{{{ r}}_{\textit{0}}}^{n-1}+{{{ r}}_{\textit{0}}}^{n-3}=0. \end{aligned}$$
(37)
Fig. 5
figure 5

The behavior of \(\rho \), \(\rho +p_{r}\) and \(\rho +p_{t}\) versus r and t respectively from left to right, for \(w=-1\), \(r_0=1\), \(R_3=1\) and \(\alpha =-0.5\) in 5-dimensions

Full size image

Thus, the spatial extension of this type of wormhole solution cannot be arbitrarily large. We then have a finite wormhole within the range \(r_{-}<r<r_{+}\). Figure 6 shows that increasing the dimension of space enlarges the wormhole spatial extension. In order to study energy conditions for these class of solutions we proceed with obtaining the behavior of the scale factor, using Eq. (25) for \(w=-1\), as

$$\begin{aligned} R \left( t \right) ={ R}_{\textit{4}}\,\cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) . \end{aligned}$$
(38)

Also, in order to check the WEC we obtain

$$\begin{aligned} \rho (r,t)= & {} \frac{ \left( n-1 \right) \left( n-2 \right) }{2{{ R}_{\textit{4}}}^{2}}\nonumber \\&+\alpha \,\left( {\frac{ \left( n-1 \right) \left( n-2 \right) }{2{{ R}_{\textit{4}}}^{4}} } \right. \nonumber \\&\left. -\frac{\left( n-1 \right) \left( {{{ r}}_{\textit{0}}}^{2}-1 \right) ^{2} \left( n-2 \right) }{2{{ R}_{\textit{4}}}^{4}{{{ r}}_{\textit{0}}}^{4}\left( \cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) \right) ^{4} }\left( \frac{r_0}{r}\right) ^{2n-2} \right) , \end{aligned}$$
(39)
$$\begin{aligned} \rho +P_r= & {} \frac{\left( {{{ r}}_{\textit{0}}}^{2}-1 \right) \left( n-2 \right) \left( n-3 \right) }{2\,{{{ r}}_{\textit{0}}}^{2}{{ R}_{\textit{4}}}^{2} \left( \cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \\&+\alpha \,\left( \frac{\left( {{{ r}}_{\textit{0}}}^{2}-1 \right) \left( n-2 \right) \left( n-3 \right) }{{{{ r}}_{\textit{0}}}^{2}{{ R}_{\textit{4}}}^{4} \left( \cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \right. \\&\left. -\frac{\left( {{{ r}}_{\textit{0}}}^{2}-1 \right) ^{2} \left( n-2 \right) \left( n-3 \right) }{{{ R}_{\textit{4}}}^{4}{{{ r}}_{\textit{0}}}^{4} \left( \cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) \right) ^{4} }\left( \frac{r_0}{r}\right) ^{2n-2}\right) , \end{aligned}$$
(40)
$$\begin{aligned} \rho +P_t= & {} -\frac{\left( {{{ r}}_{\textit{0}}}^{2}-1 \right) \left( n-3 \right) }{2{{{ r}}_{\textit{0}}}^{2}{{ R}_{\textit{4}}}^{2} \left( \cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1} \nonumber \\&-\alpha \,\left( \frac{\left( {{{ r}}_{\textit{0}}}^{2}-1 \right) \left( n-3 \right) }{{{{ r}}_{\textit{0}}}^{2}{{ R}_{\textit{4}}}^{4} \left( \cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) \right) ^{2} }\left( \frac{r_0}{r}\right) ^{n-1}\nonumber \right. \\&\left. +\frac{\left( {{{ r}}_{\textit{0}}}^{2}-1 \right) ^{2} \left( n+1 \right) }{{{ R}_{\textit{4}}}^{4}{{{ r}}_{\textit{0}}}^{4} \left( \cosh \left( {\frac{t}{{ R}_{\textit{4}}}} \right) \right) ^{4} }\left( \frac{r_0}{r}\right) ^{2n-2}\right) . \end{aligned}$$
(41)
Fig. 6
figure 6

The behavior of \(1-b(r)/r\) with respect to r for \(r_0=0.1\), \(n=9,7,5\) from up to down, respectively

Full size image

In this case, we see that in GR (\(\alpha =0\)), \(\rho +P_t\) is always negative, implying the violation of NEC throughout the spacetime. However, we can choose a suitable value of \(\alpha \) so that we have normal matter in the whole spacetime. In Fig. 7, we depict the quantities \(\rho \) , \(\rho +P_r\) and \(\rho +P_t\) in terms of r and t for \( { R}_{\textit{4}}=1, r_0=0.1\) and \(n=5\).

4 Concluding remarks

In this paper, we have explored higher-dimensional dynamical wormhole solutions in the framework of GB gravity by considering a constraint on the Ricci scalar. In this context, the existence of higher curvature may help to construct wormhole solutions that respect energy conditions. In a cosmological set up, microscopic dynamical wormholes produced in the early universe may be inflated to macroscopic scales. We found that choosing a suitable value for \(\alpha \) parameter and wormhole throat could help to obtain wormholes without the need for exotic matter. We have also briefly presented solutions in higher dimensional Einstein gravity, \(\alpha =0\), that confirms previous results outlined in [82]. Furthermore, for a specific value of w the WEC is satisfied throughout the entire spacetime in four dimensions. Also, we found new solutions that have finite size for which the WEC can be satisfied for negative GB constant.

Fig. 7
figure 7

The behavior of \(\rho \), \(\rho +p_{r}\) and \(\rho +p_{t}\) versus r and t respectively from left to right, for \(w=-1\), \(r_0=0.1\), \(R_4=1\) and \(\alpha =-0.5\) in 5-dimensions

Full size image

Finally, it should be noted that during the past years, several branches of theoretical physics such as string theory, supergravity, Kaluza–Klein theory have predicted the presence of extra dimensions [105, 106]. Hence, it makes sense to seek for possible existence of geometrical objects within spacetimes with the number of dimensions greater than four as for example higher dimensional black holes and wormholes [107,108,109]. From astrophysical perspective, the near horizon black hole solutions in higher dimensional models are important since they can be regarded as windows to extra dimensions [110, 111], and in cosmological scenarios the possible existence of extra dimensions is significant during the evolution of the early universe [112,113,114]. In [115] the author has provided some observational criterion in order to determine whether the extra dimensions are compact or large and phenomenological aspects of large, warped, and universal extra dimensions is reviewed in [116]. Wormhole geometries without exotic matter have been studied in [117]. Such solutions could be thought of as similar to missing energies in collider phenomenology which are expected to provide signals of the existence of extra dimensions [118]. Therefore, the existence of such configurations with extra dimensions in our universe cannot be a priori excluded, and their possible astrophysical results could be a subject of further studies.