1 Introduction

The AdS/CFT correspondence relates the weak gravitational theory in the anti-de Sitter spacetime to the strong quantum field theory lived on its conformal boundary, and thus provides us a new theoretical framework to study the strongly coupled systems [1, 2]. Over the past years, the AdS/CFT correspondence(or its generalized version, the gauge/gravity duality) has been intensively applied in many aspects in condensed systems [3,4,5,6,7,8,9], especially the high \(T_c\) superconductor (s-wave), which was realized successfully via an Einstein–Maxwell theory coupled to a complex scalar field in the Schwarzschild-AdS black hole in the probe limit [10, 11]. After that, the holographic superconductor model was extended to the SU(2) p-wave superconductor model [12], d-wave superconductor model [13], the insulator/superconductor model [14], the competition and coexistence of two order parameters [15,16,17,18], Sturm–Liouville (S–L) method [19,20,21], the backreaction from the matter field to the gravitational background [22], the effects of external magnetic field [23, 24] as well as the lattice effects [25,26,27,28,29], see, for example, Refs. [30,31,32] for reviews.

On the other hand, in order to understand the influences of the \(\frac{1}{\lambda }\) (\(\lambda \) is the ’t Hooft coupling) corrections on the holographic superconductor models, many works took into account the high curvature correction [33,34,35,36] and nonlinear electrodynamics [36], such as the Born–Infeld term [21, 37, 38], the Power-Maxwell term [33, 34], Logarithmic term [39] and exponential term [40]. The results showed that both high curvature correction and nonlinear electrodynamics parameters hinder the conductor/superconductor phase transition. In addition, considering the Weyl term \(CF^2\) composed of the coupling of the Weyl tensor \(C_{\mu \nu }^{\rho \sigma }\) and the Maxwell field strength \(F_{\alpha \beta }\), which was firstly introduced to realize the breakdown of the electromagnetic self-duality from a holographic perspective [41], Refs. [42, 43] studied the effects of the \(\frac{1}{\lambda }\) corrections on the s-wave superconductor model, and found that the increasing Weyl correction enhances the condensate and decreases the ratio of the energy gap to the critical temperature. Subsequently, the author in Ref. [44] proposed a general high derivative theory which extends the correction term in Refs. [42, 43], and obtained an arbitrarily sharp Drude-like peak in the optical conductivity. Thereafter, Refs. [45,46,47,48,49] studied the influences of the \(C^2F^2\) term (i.e., the 6 derivative term \(C_{\mu \nu }^{\alpha \beta }C_{ \alpha \beta }^{\mu \nu }F_{\rho \sigma }F^{\rho \sigma }\)) on the s-wave conductor/superconductor model via the numerical and analytical method, respectively. It was observed that the increasing \(C^2F^2\) parameter enhances the superconductor phase transition and results in a wider extension of the superconducting energy gap.

As for the holographic superconductor model, in addition to the SU(2) p-wave model, by imitating the holographic s-wave superconductor model, authors of Ref. [50] realized a magnetic-field-induced vector condensate via a Maxwell-complex-vector (MCV) field with a mass and further found that this model is a generalization of the SU(2) p-wave model with a mass, which was verified in Refs. [51,52,53]. Subsequently, the MCV p-wave model was extended to the electric-field-induced superconductor model [54,55,56] and the case of the backreaction from matter field to the gravitational background [17, 18, 57,58,59,60]. In particular, the model showed the abundant phase structure, such as “zero-order phase transition” and “the retrograde condensate” in the four-dimensional AdS black holes [17, 18, 57,58,59]. However, the order of the phase transition is always \(\frac{1}{2}\) in the three-dimensional BTZ (Bandos–Teitelboim–Zanelli) black hole although the increasing backreaction makes the condensate harder to form [60]. Meanwhile, in order to investigate the \(\frac{1}{\lambda }\) effects, the MCV p-wave superconductor model was constructed in Lifshitz gravity [61], by including nonlinear electrodynamics [62,63,64] and the \(RF^2\) correction [65, 66]. Concretely, the authors in Ref. [63] built an one-dimensional holographic p-wave superconductors by coupling Born–Infeld (BI) electrodynamics in the BTZ black hole and reproduced the interesting Drude-like peak in the real part of conductivity. Thereafter, by considering the general nonlinear electrodynamics with high order correction, Ref. [64] realized the p-wave superconductors in both Einstein gravity and Gauss–Bonnet gravity. It was found that the behavior of conductivity generally depends on the choice of the mass of the vector field, the nonlinear and the Gauss–Bonnet parameters. Besides, authors in Ref. [67] studied the effect of the Weyl correction (\(CF^2\)) on the MCV p-wave superconductor model and found that the Weyl correction does not influence the properties of the insulator/superconductor phase transition but obviously enhances the conductor/superconductor phase transition.

As mentioned above, although the \(C^2F^2\) correction is 6 derivative, it still reproduces many significant influences on the properties of the superconductor. At the moment, an interesting question is how the \(C^2F^2\) correction affects the MCV p-wave superconductor model, and whether the \(C^2F^2\) correction can induce the Drude-like peak in the conductivity in the p-wave model. Motivated by the fact that answering above questions can not only extend the applied range of the gauge/gravity duality but also understand further the \(\frac{1}{\lambda }\) effects on the superconductor models, we will study systematically the influence of the \(C^2F^2\) correction on the MCV p-wave superconductor model, which can be regarded as the generalization of the Weyl correction [67]. The results show that the larger \(C^2F^2\) parameter enhances the superconductor phase transition, and the analytical results agree well with the numerical results. In addition, at the critical point, the real part of conductivity displays a Drude-like peak at the low frequency as well as an obviously pronounced peak at the intermediate frequency due to the presence of the \(C^2F^2\) coupling. Especially, the effect of the \(C^2F^2\) parameter on the ratio of the energy gap to the critical temperature is consistent with the phase diagram of the critical temperature versus the \(C^2F^2\) parameter.

This paper is organized as follows. In Sect. 2, we construct the MCV p-wave superconductor model and mainly study the effects of the 6 derivative on the critical temperature and the condensate as well as the conductivity. The final section is devoted to the conclusions and discussions.

2 Holographic superconductor model

In this section, we firstly give the setup of the holographic superconductor model and then mainly study numerically the effects of the \(C^2F^2\) correction on the vector condensate, grandpotential as well as the frequency dependent conductivity, following which we recalculate the critical temperature and the critical behavior of the vector condensate by the S–L method to backup the numerical results.

The four-dimensional Schwarzschild-AdS black hole is of the form [10, 11]

$$\begin{aligned} ds^2= & {} -f(r)dt^2+\frac{dr^2}{f(r)}+r^2\left( dx^2+dy^2\right) ,f(r)\nonumber \\= & {} r^2 \left( 1-\frac{r_+^3}{r^3}\right) , \end{aligned}$$
(1)

where \(r_+\) represents the horizon satisfying \(f(r_+)=0\). Meanwhile, the Hawking temperature reads \(T=\frac{3r_+}{4\pi }\).

Following Refs. [17, 18, 44, 45, 50, 51], we consider the Lagrangian density consisting of a complex vector field and a Maxwell field coupled to the Weyl tensor as

$$\begin{aligned} \mathcal {L}_m= & {} -\frac{1}{8}F_{\mu \nu }X^{\mu \nu \rho \sigma } F_{\rho \sigma }-\frac{1}{2}\rho _{\mu \nu }^\dag \rho ^{\mu \nu }\nonumber \\&-m^2\rho ^\dag _\mu \rho ^\mu +iq\gamma _0\rho _\mu \rho ^\dag _\nu F^{\mu \nu }, \end{aligned}$$
(2)

where the antisymmetry tensor \(\rho _{\mu \nu }=D_\mu \rho _\nu -D_\nu \rho _\mu \) and the tensor \(X_{\mu \nu }^{\rho \sigma }\) is an infinite family of high derivative terms, i.e.,

$$\begin{aligned} X_{\mu \nu }^{\rho \sigma }= & {} I_{\mu \nu }^{\rho \sigma }-8 \gamma _{1,1}L^2 C_{\mu \nu }^{\rho \sigma }-4L^2\gamma _{2,1}C^2 I_{\mu \nu }^{\rho \sigma }\nonumber \\&-8L^4\gamma _{2,2}C_{\mu \nu }^{\alpha \beta }C_{\alpha \beta }^{\rho \sigma }\nonumber \\&-4L^6\gamma _{3,1}C^3 I_{\mu \nu }^{\rho \sigma }-8L^6 \gamma _{3,2}C^2I_{\mu \nu }^{\rho \sigma }\nonumber \\&-8L^6\gamma _{3,3}C_{\mu \nu }^{\alpha _1\beta _1}C_{ \alpha _1\beta _1}^{\ \alpha _2\beta _2}C_{ \alpha _2\beta _2}^{\rho \sigma } +\cdots . \end{aligned}$$
(3)

In detail, \(I_{\mu \nu }^{\rho \sigma }=\delta _\mu ^{\ \rho }\delta _\nu ^{\ \sigma }-\delta _\mu ^{\ \sigma }\delta _\nu ^{\ \rho }\) is an identity matrix and \(C^n=C_{\mu \nu }^{\alpha _1\beta _1}C_{ \alpha _1\beta _1}^{\alpha _2\beta _2}\cdots C_{ \alpha _{n-1}\beta _{n-1}}^{\ \mu \nu }\) with \(C_{\mu \nu }^{\rho \sigma }\) the Weyl tensor. Furthermore, \(D_\mu =\nabla _\mu -iq A_\mu \), \(F_{\mu \nu }=\nabla _\mu A_\nu -\nabla _\nu A_\mu \) and m (q) is the mass (charge) of the vector field \(\rho _\mu \). What is more, we do not consider the magnetic field effects on the superconductor phase transition, so the last term with the constant \(\gamma _0\) in Eq. (2) can be ignored, which characterizes the strength of interaction between \(\rho _\mu \) and \(F_{\mu \nu }\). In the remainder of this paper, we will only turn on the 6 derivative term \(-\frac{1}{8}F^{\mu \nu }(-4L^2\gamma _{2,1}C^2 I_{\mu \nu }^{\rho \sigma }) F_{\rho \sigma }=L^2\gamma _{2,1}C^2F^2\) with other \(\gamma _{i,j}\) terms vanishing. For simplicity, we take \(\gamma _{2,1}=\gamma \) throughout the paper. Considering the fact that we will solve the equation of the gauge field perturbatively in terms of the 6 derivative parameter \(\gamma \), so we restrict the range of the parameter \(\gamma \) as \(\gamma \in [-\frac{1}{50},\frac{1}{50}]\) combining with the arguments in Refs. [44, 45]. In addition, we will set \(L=1\) and \(q=1\) and work in the so-called probe approximation where the equations of motion related to the vector field and the gauge field decouple from the equations of motion for gravitational sector and the main physical results are believed to be still grasped.

Fig. 1
figure 1

The condensate versus the temperature with \(\gamma =-\frac{1}{50}\) (black solid), \(\gamma =0\) (red dashed), \(\gamma =\frac{1}{50}\) (blue dot dashed) in the left panel and the critical temperature versus the \(C^2F^2\) parameter \(\gamma \) in the right panel

Full size image
Table 1 The critical temperature in unit of chemical potential \(\mu \) from the numerical method (\(T_{cn}\)) and the analytical method (\(T_{ca}\)) for different value of \(\gamma \)
Full size table

Varying the action (2) with respect to the vector \(\rho _\mu \) and the gauge field \(A_\mu \), respectively, we can obtain the equations of motion

$$\begin{aligned}&D_\mu \rho ^{\mu \nu }-m^2\rho ^\nu +i \gamma _0 \rho _\mu F^{\mu \nu }=0, \end{aligned}$$
(4)
$$\begin{aligned}&\frac{1}{2}\nabla _\mu (X^{\mu \nu \rho \sigma } F_{\rho \sigma })-i \gamma _0\nabla _\mu \left( \rho ^{\mu }(\rho ^{\nu })^\dag -\rho ^{\nu }(\rho ^{\mu })^\dag \right) \nonumber \\&\quad +i\left( (\rho _\mu )^\dag \rho ^{\mu \nu }-\rho _\mu (\rho ^{\mu \nu })^\dag \right) =0. \end{aligned}$$
(5)

To build the p-wave superconductor induced by the electric field, the ansatzs for the vector field \(\rho _\mu \) and the gauge field \(A_\mu \) can be taken as the following form

$$\begin{aligned} \rho _\nu dx^\nu= & {} \psi _x(r)dx, \ A_\nu dx^\nu =\phi (r) dt, \end{aligned}$$
(6)

with other components vanishing.

Choosing \(\psi _x(r)\) and \(\phi (r)\) as real functions and substituting the above ansatzs (6) into Eqs. (4) and (5) yields

$$\begin{aligned} \psi _x''+\left( \frac{f'}{f}+\frac{2}{r}\right) \psi _x ' +\left( \frac{\phi ^2}{r^4f^2}-\frac{m^2}{r^2f}\right) \psi _x= & {} 0, \end{aligned}$$
(7)
$$\begin{aligned} \phi ''+\left( \frac{2}{r}+\frac{X^\prime _3}{X_3}\right) \phi ' -\frac{2\psi ^2}{r^4fX_3}\phi= & {} 0, \end{aligned}$$
(8)

where the prime stands for the derivative with respect to r and the nonvanishing components of the tensor \(X_{\mu \nu }^{\rho \sigma }\) are denoted as \(X_A^{\ B}={X_1(r),X_2(r),X_3(r),X_4(r),X_5(r),X_6(r)}\) with \(A,B\in {(tx,ty,tr,xy,xr,yr)}\). In particular, \(X_{tx}^{tx}=X_{ty}^{ty}=X_{tr}^{tr}=X_{xy}^{xy}=X_{xr}^{xr}=X_{yr}^{yr}=1-\frac{4}{3} \gamma \left( r^2f''+2r f'\right) ^2\). Obviously, for the special case \(\gamma =0\), Eqs. (7) and (8) reduce to Eq. (38) in Ref. [50], Eqs. (6) and (7) in Ref. [55] with \(A_y=0\), and Eqs. (6) and (7) in Ref. [61] in the case of \(z=1\) and \(A_y=0\). However, the equation of motion corresponding to Eq. (8) in the five-dimensional AdS case is not identical with Eq. (36) in Ref. [67], from which we can believe the present model will generalize some new characters of superconductor.

To solve the above equations, we should impose the boundary conditions. At the horizon, the vector field \(\psi _x\) is required to be regular, while the gauge field \(A_\mu \) should satisfy the condition \(\phi (r_+)=0\) to ensure the finite form of \(g^{\mu \nu }A_\mu A_\nu \). At the boundary (\(r\rightarrow \infty \)), \(\psi _x(r)\) and \(\phi (r)\) behave as

$$\begin{aligned} \psi _x(r)= & {} \frac{\psi _{x-}}{r^{\Delta _-}}+\frac{\psi _{x+}}{r^{\Delta _+}} +\cdots , \end{aligned}$$
(9)
$$\begin{aligned} \phi (r)= & {} \mu -\frac{\rho }{r}+\cdots , \end{aligned}$$
(10)

where \(\Delta _\pm =\frac{1}{2}(1\pm \sqrt{1+4m^2})\) with the Breitenlohner–Freedman (BF) bound of the mass \(m^2\ge m_{BF}^2= -\frac{1}{4}\). According to the gauge/gravity duality, the coefficient \(\psi _{x-}\)(\(\psi _{x+}\)) is regarded as the source (the vacuum-expectation value) of the boundary operator \({\hat{J}}_x\), while \(\mu \) (\(\rho \)) is interpreted as the chemical potential (the charge density) in the dual field theory. To guarantee the spontaneous breaking of U(1) gauge symmetry in the system, we require that the source of the condensate vanishes, i.e., \(\psi _{x-}=0\). We take \(\Delta =\Delta _+=\frac{3}{2}\) throughout the paper, which means that the mass squared \(m^2\) of the vector field \(m^2=\frac{3}{4}\).

There is an important scaling symmetry for the above system, i.e., \((r, T, \mu )\rightarrow \lambda _0(r, T, \mu ), \psi _{x+} \rightarrow \lambda _0^{5/2}\psi _{x+}, \rho \rightarrow \lambda _0^2\rho \) with the positive constant \(\lambda _0\), by using which we can fix the chemical potential \(\mu \) of the system and thus work in the grand canonical ensemble.

2.1 Numerical part

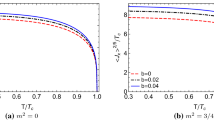
After series of numerical calculations, we obtain the condensate as a function of the temperature for various \(C^2F^2\) parameter \(\gamma \) and display the condensate for \(\gamma =-\frac{1}{50},0,~\frac{1}{50}\) in the left panel of Fig. 1. It is observed that there always exists a critical temperature below which the vector condensate starts to appear outside the horizon. Meanwhile, from the fitness of the condensate curve, we can further find all curves of condensate versus the temperature have a square root behavior near the critical value, which indicates that the system may suffer from a second-order phase transition at the critical point. Furthermore, at the lower temperature, the vector condensate saturates a stable value, which decreases with the increasing \(C^2F^2\) parameter. As argued in Refs. [10, 60], the larger gap in the condensate curve suggests the stronger interaction in the system, which might means that the increasing \(C^2F^2\) parameter inhibits the conductor/superconductor phase transition. In addition, we also consider the case for other value of \(\gamma \) in the range \(\gamma \in [-\frac{1}{50},-\frac{1}{50}]\), the results show that the effects of the \(C^2F^2\) correction is qualitative the same. Especially, in the case of \(\gamma =0\), the results restore to the pure AdS superconductor, i.e., the results in Ref. [55] and the ones with the dynamical critical exponent \(z=1\) in Ref. [61] as well as the results with the vanishing backreaction from the matter field to the gravity [57,58,59].

To study systemically the effects of the \(C^2F^2\) correction on the superconductor phase transition, we plot the critical temperature with respect to the \(C^2F^2\) parameter \(\gamma \) in the right panel of Fig. 1 and list the related results in Table 1, from which we find that the critical temperature calculated from the numerical method increases with the increasing \(C^2F^2\) parameter \(\gamma \), which means that the increasing \(C^2F^2\) correction makes the superconductor phase transition easier. In particular, in the case of \(\gamma =0\), the results return to the ones in Refs. [55, 61] and agree with the ones for the case of \(b=0\) and \(d=4\) in Ref. [63]. Meanwhile, we find that the effect of the \(C^2F^2\) correction on the superconductor phase transition is similar to the one of the Weyl correction(\(CF^2\)) on the superconductor model in Ref. [67] but in contrast to the influence of the pure high curvature correction [33,34,35,36] or the nonlinear electrodynamics [33, 34, 37,38,39] on the superconductor model.

To check that below the critical point the superconducting state is indeed thermodynamically favored, it is helpful to calculate the grand potential and compare the one of the hairy state with that of the normal state, which is defined by the Euclidean on-shell action \(S_E\) timing the temperature of the black hole, i.e., \(\Omega =T S_E\). Integrating the Minkowski action (2) by parts yields the on-shell part of action as

$$\begin{aligned} S_{os}= & {} \int \sqrt{-g}d^4x\left( -\frac{1}{4}\nabla _\mu \left( A_\nu X^{\mu \nu \rho \sigma }F_{\rho \sigma }\right) +\frac{1}{4} A_\nu \nabla _\mu (X^{\mu \nu \rho \sigma }F_{\rho \sigma }) \right. \\&\left. -\nabla _\mu \left( \rho _\nu ^\dag \rho ^{\mu \nu }\right) +\rho _\nu ^\dag \left( D_\mu \rho ^{\mu \nu } -m^2\rho ^\nu +i q \gamma \rho _\mu F^{\mu \nu } \right) \right) \\= & {} \int d^3x \sqrt{-h} n_r\left( -\frac{1}{4} A_\nu X^{r\nu \rho \sigma } F_{\rho \sigma }- \rho _\nu ^\dag \rho ^{r\nu }\right) |_{r\rightarrow \infty }\\&+ \frac{1}{4}\int \sqrt{-g}d^4xA_\nu \nabla _\mu \left( X^{\mu \nu \rho \sigma } F_{\rho \sigma }\right) \\= & {} \frac{V_2}{T}\left( \frac{1}{2}\mu \rho -\int ^\infty _{r_+}\frac{\phi ^2\psi ^2}{r^2f}dr\right) , \end{aligned}$$

where we have taken into account \(\int dx dy =V_2\), \(\int dt=\frac{1}{T}\) and also Eqs. (4) and (5). Remind that \(S_E=-S_{os}\), we obtain the density of the grand potential as

$$\begin{aligned} \frac{\Omega }{V_2}=\frac{-TS_{os}}{V_2}=-\frac{1}{2}\mu \rho +\int ^\infty _{r_+}\frac{\phi ^2\psi ^2}{r^2f}dr. \end{aligned}$$
(11)
Fig. 2
figure 2

The grand potential of the superconducting state(red solid) and the normal state (black dashed) as a function of the temperature with the \(C^2F^2\) parameter \(\gamma =-\frac{1}{50}\) (left) and \(\gamma =\frac{1}{50}\) (right)

Full size image

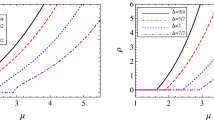
We typically display the grand potential as a function of the temperature for the case of \(\gamma =-\frac{1}{50}\) and \(\gamma =\frac{1}{50}\) in Fig. 2, from which we find that near the critical temperature, the red solid curve corresponding to the superconducting state stretches out from the black dashed curve corresponding to the normal state smoothly with the decreasing temperature. Most importantly, the value of the grand potential of the superconducting state is always lower than that of the normal state, which means that the superconducting state is indeed thermodynamically stable below the critical temperature. Furthermore, comparing the curve of the superconducting state with the one of the normal state, we can obtain a fact that at the critical temperature, the system indeed suffers from a second-order phase transition, which agrees with the behavior of the condensate in Fig. 1. In addition, we also consider the other parameter cases for \(\gamma \in [-\frac{1}{50},\frac{1}{50}]\) and obtain the similar results to the cases of \(\gamma =-\frac{1}{50}\) and \(\gamma =\frac{1}{50}\). In particular, as \(\gamma =0\), the results return to the pure AdS case [50]. As a result, it is believed our numerical results are reliable in the total parameter space considered in the present work.

On the other hand, as we all know, the infinite DC conductivity is one typical signal of superconductors. Meanwhile, the energy gap of the electric conductivity can help us to estimate how strong the interaction involves in the superconductor. As a result, it is meaningful to compute the AC conductivity of the superconductor model. From the AdS/CFT correspondence, to calculate the conductivity in the boundary field theory, we need study the perturbation of the gauge field in the bulk. For simplicity, we turn on the perturbation along the y direction with the ansatz \(\delta A_y(t,r)=A_y(r)e^{-i \omega t}\). The linearized equation of the perturbation \(A_y(r)\) is derived as

$$\begin{aligned}&A_y''+\left( \frac{2}{r}+\frac{f'}{f}+\frac{X^\prime _6}{X_6}\right) A_y'\nonumber \\&\quad +\left( \frac{\omega ^2X_2}{r^{4}f^2X_6}-\frac{2\psi ^2}{r^{4}fX_6}\right) A_y=0. \end{aligned}$$
(12)

At the horizon, we impose the ingoing wave condition

$$\begin{aligned}&A_y(r)=(r-r_+)^{-i\omega /{4\pi T}}\nonumber \\&\quad \left( 1+A_{y1} (r-r_+)+A_{y2} (r-r_+)^2+A_{y3}(r-r_+)^3+\cdots \right) .\nonumber \\ \end{aligned}$$
(13)

At the boundary, the asymptotical expansion of \(A_x(r)\) is expressed as

$$\begin{aligned} A_y(r)=A^{(0)}+\frac{A^{(1)}}{r}+\cdots . \end{aligned}$$
(14)

Combining with Eqs. (2) and  (14), we can obtain the retarded Green’s function as

$$\begin{aligned} G=-\lim _{r\rightarrow \infty }r^2fX_6\frac{A^\prime _y}{A_y}, \end{aligned}$$
(15)

where the prime still represents the derivative with respect to r. According to the Kubo formula, the AC conductivity reads

$$\begin{aligned} \sigma (\omega )= & {} -\frac{I}{\omega }G=-\frac{I}{\omega }\frac{A^{(1)}}{A^{(0)}}. \end{aligned}$$
(16)

In Fig. 3, we plot the frequency dependent AC conductivity at the critical temperature(\(\frac{T}{T_c}=1\)) for \(\gamma =-\frac{1}{50}\), 0 and \(\frac{1}{50}\), respectively. It is observed from the real part of conductivity that a Drude-like peak appears at the low frequency for the case of \(\gamma =-\frac{1}{50}\) compared with the horizontal line corresponding to \(\gamma =0\). It should be noted that the current Drude-like peak is produced by the promoting conductivity near zero frequency, which is different from the one formed in the BTZ black hole in Ref. [63]. Meanwhile, for the case of \(\gamma =\frac{1}{50}\), we can obtain an obviously pronounced peak at the intermediate frequency. What is more, from the real part of conductivity, even the DC conductivity with \(\gamma =\frac{1}{50}\) is very small, we find it is still finite from the no-pole of the imaginal part of the conductivity. The above new behaviors generated by the \(C^2F^2\) correction are similar to the case of the s-wave model in Refs. [42, 43].

Fig. 3
figure 3

The real part(left) and imaginal part(right) of the AC conductivity as a function of the frequency with \(\gamma =-\frac{1}{50}\) (black solid), \(\gamma =0\) (red dashed) and \(\gamma =\frac{1}{50}\) (blue dotdashed)(calculated at \(\frac{T}{T_c}= 1\))

Full size image
Fig. 4
figure 4

The left panel denotes the real part of the conductivity in the case of \(\gamma =-\frac{1}{50}\) (black solid),\(\gamma =0\) (red dashed) and \(\gamma =\frac{1}{50}\) (blue dotdashed), while the right panel represents the ratio of energy gap to the critical temperature as a function of the \(C^2F^2\) correction \(\gamma \) (calculated at \(\frac{T}{T_c}\approx \frac{1}{10}\))

Full size image

In addition, we also show the AC conductivity at the lower temperature \(\frac{T}{T_c}\approx \frac{1}{10}\) for different \(C^2F^2\) parameter \(\gamma \) in the left panel of Fig. 4. From the overall trend of the conductivity, we find the conductivity with nonvanishing \(\gamma \) is similar to the Maxwell case with \(\gamma =0\) [10], even the nonlinear electrodynamics case [39]. For example, at the vanishing frequency, there exists a pole in the imaginal part of conductivity corresponding to a delta function in the real part of conductivity which means the infinite DC conductivity expected from the superconductor. At the intermediate frequency, the real part of the conductivity increases quickly with the improving frequency which corresponds to a minimum in the imaginal part of the conductivity, i.e., the energy gap of the superconductor (\(\omega _g\)). The calculation show that \(\frac{\omega _g}{T_c}\approx 9.172\) for \(\gamma =-\frac{1}{50}\) and \(\frac{\omega _g}{T_c}\approx 8.107\) for \(\gamma =0\) as well as \(\frac{\omega _g}{T_c}\approx 4.582\) for \(\gamma =\frac{1}{50}\) which is (much) larger than the value of BCS superconductors (\(\frac{\omega _g}{T_c}\approx 3.54\)) and thus reflects the strong interaction in our holographic superconductor. To see the effect of the \(C^2F^2\) correction on the energy gap, we display the ratio of the energy gap to the critical temperature (\(\frac{\omega _g}{T_c}\)) as a function of the \(C^2F^2\) parameter \(\gamma \) in the right panel of Fig. 4. It is clear that the energy gap decreases with the increasing \(\gamma \) which agrees well with the behavior of the condensate and also the phase diagram about the critical temperature in Fig. 1.

2.2 Analytical part

To check further the reliability of the numerical result, especially the critical temperature, in what follows, we resolve the coupled equations (7) and (8) via the S–L eigenvalue method [19, 48, 67]. It should be noted that almost all the previous literature in terms of the analytical S–L superconductor model worked in the canonical ensemble [19, 48, 67], where the charge density is fixed. However, in the present paper worked in the grand ensemble with the fixed chemical potential, we should be careful in the following calculation, especially, the choice of the boundary condition in the course of solving Eq. (8).

By introducing a new variable \(z=\frac{r_+}{r}\), Eqs. (7) and (8) can be expressed as

$$\begin{aligned}&\psi ''(z)+\frac{3 z^2}{z^3-1}\psi '(z)+\left( \frac{m^2 }{ z^2\left( z^3-1\right) }\right. \nonumber \\&\quad \left. + \frac{ \phi (z)^2}{r_+^2\left( z^3-1\right) ^2}\right) \psi (z)=0, \end{aligned}$$
(17)
$$\begin{aligned}&\phi ''(z)+\frac{288\gamma z^5}{48 \gamma z^6-1}\phi '(z)\nonumber \\&\quad -\frac{2 \psi (z)^2}{r_+^2 \left( z^3-1\right) \left( 48 \gamma z^6-1\right) } \phi (z)=0, \end{aligned}$$
(18)

where the prime denotes the derivative with respect to z. When \(T= T_c\), the condensate vanishes, i.e., \(\psi (z)=0\), so we can rewrite Eq. (18) as

$$\begin{aligned} \phi ''(z)+\frac{288\gamma z^5}{48 \gamma z^6-1}\phi '(z)=0. \end{aligned}$$
(19)

Due to the existence of the \(C^2F^2\) parameter \(\gamma \), in general, it is difficult to give the exact solution to Eq. (19). However, by considering the parameter \(\gamma \) as a small quantity, we can solve Eq. (19) perturbative order by order. Up to the fourth order of \(\gamma \), the solution to \(\phi (z)\) is given by

$$\begin{aligned} \frac{\phi (z)}{r_{+c}}= & {} \lambda \phi _1(z)=\lambda \left( 1-z + \gamma \xi _1(z) +\gamma ^2\xi _2(z)\right. \nonumber \\&\left. +\gamma ^3\xi _3(z)+\gamma ^4\xi _4(z)\right) , \end{aligned}$$
(20)

where \(r_{+c}\) is the location of the horizon at \(T=T_c\) and the functions \(\xi _1(z)=48 z(1-z^6)/7\), \(\xi _2(z)=(82944 z+29952 z^7-112896 z^{13})/637\), \(\xi _3(z)=(314523648 z+75644928 z^7+102961152 z^{13}-493129728 z^{19})/84721\), and \(\xi _4(z)=(23878507954176 z+4906568908800 z^7+4447921766400 z^{13}+7692823756800 z^{19}-40925822386176 z^{25})/192740275\), respectively.

Comparing the above solution of \(\phi (z)\) with Eq. (10), we can derive the constant \(\lambda \) as

$$\begin{aligned} \lambda =\frac{\mu }{r_{+c}}. \end{aligned}$$
(21)

The asymptotical solution of \(\psi (z)\) is defined by a trial function F(z) as

$$\begin{aligned} \psi (z) = \frac{\langle {\hat{J}}_x\rangle }{r_+^{\Delta }}z^{\Delta }F(z). \end{aligned}$$
(22)

Substituting Eqs. (20) and (22) into Eq. (17) yields

$$\begin{aligned}&F''(z)+\frac{(2 \Delta +3) z^3-2 \Delta }{z \left( z^3-1\right) }F'(z) \nonumber \\&\quad +\frac{m^2+\Delta \left( 1-\Delta +(\Delta +2) z^3\right) }{z^2 \left( z^3-1\right) }F(z)\nonumber \\&\quad +\lambda ^2\frac{ \phi _1 (z)^2}{\left( z^3-1\right) ^2}F(z)=0. \end{aligned}$$
(23)

According to the condition of F(z), i.e., \(F(0)=1\) and \(F^\prime (0)=0\) [19,20,21], we take the ansatz of F as

$$\begin{aligned} F=F_\alpha (z)\equiv 1-\alpha z^2, \end{aligned}$$
(24)

with \(\alpha \) to be determined. Therefore, Eq. (23) can be transformed to the S–L eigenvalue equation

$$\begin{aligned} (\mathcal {T}F^{\prime })^\prime -\mathcal {P}F+\lambda ^2 \mathcal {Q}F=0, \end{aligned}$$
(25)

where the coefficients are respectively

$$\begin{aligned} \mathcal {T}= & {} \left( 1-z^3\right) z^{2 \Delta },\quad \mathcal {P} = z^{2 \Delta -2}\nonumber \\&\left( m^2+\Delta \left( 1-\Delta +(\Delta +2) z^3\right) \right) , \nonumber \\ \mathcal {Q}= & {} \frac{z^{2 \Delta } \phi _1(z)^2}{1-z^3}. \end{aligned}$$
(26)

The eigenvalue of \(\lambda ^2\) minimizes the expression with respect to the parameter \(\alpha \) as

$$\begin{aligned} \lambda ^2(\alpha ,\gamma ,z) = \frac{\int ^{1}_{0}(\mathcal {T}{F'}^2-\mathcal {P}F^2)dz}{\int ^{1}_{0}\mathcal {Q} F^2 dz}. \end{aligned}$$
(27)

The critical temperature reads

$$\begin{aligned} T_{c} = \frac{3}{4\pi \lambda }\mu . \end{aligned}$$
(28)

We plot the analytical critical temperature as a function of the \(C^2F^2\) parameter \(\gamma \) in the right panel of Fig. 1 and also list the analytical results in Table 1 for comparison with the numerical results, from which we can see clearly that the analytical critical temperature increases with the improving \(C^2F^2\) parameter \(\gamma \), which agrees well with the numerical results and indicates that the analytical S–L method is still powerful in the grand canonical ensemble.

Below (but close to) the critical temperature, the vector condensate is very small. Thus we can expand \(\phi (z)\) in the small parameter as

$$\begin{aligned} \frac{\phi (z)}{r_+}=\lambda \phi _1(z)+\left( \frac{\langle {\hat{J}}_x \rangle }{r_+^{\Delta +1}}\right) ^2\chi (z). \end{aligned}$$
(29)

At the boundary \((z\rightarrow 0)\), the function \(\chi (z)\) can be expand series as \(\chi (z)=\chi (0)+\chi '(0)z+\cdots \), and then matching Eq. (29) with Eq. (10), we can obtain

$$\begin{aligned} \lambda +\chi (0)\left( \frac{\langle {\hat{J}}_x \rangle }{r_+^{\Delta +1}}\right) ^2=\frac{\mu }{r_+}. \end{aligned}$$
(30)

Next the main task is to find the value of \(\chi (0)\). Substituting Eq. (29) and (22) in Eq. (18) yields the equation of \(\chi (z)\) at the order of \(\langle {\hat{J}}_x \rangle ^2\) as

$$\begin{aligned} \chi '' (z) + \frac{288\gamma z^5\chi ' (z)}{48\gamma z^6 -1} - \frac{2\lambda z^3 F (z)^2\phi _1 (z)}{\left( z^3 - 1 \right) \left( 48\gamma z^6 -1\right) }=0. \end{aligned}$$
(31)

Usually, we still take the boundary conditions as \(\chi (1)=0=\chi '(1)\) [19, 20, 48]. Multiplying the factor \((-1 + 48\gamma z^6 )\) to Eq. (31), we can read

$$\begin{aligned} ((-1 + 48 \gamma z^6 )\chi '(z))'=2\lambda \frac{z^3 \phi _1 (z) F(\alpha ,z)^2}{z^3-1}. \end{aligned}$$
(32)

Taking into account the condition \(\chi '(1)=0\) and integrating Eq. (32), we get

$$\begin{aligned} -(-1 + 48 \gamma z^6 )\chi '(z)= & {} 2\lambda \int ^{{\tilde{z}}=1}_{{\tilde{z}}=z}\frac{{\tilde{z}}^{3} \phi _1 ({\tilde{z}}) F(\alpha ,{\tilde{z}})^2}{{{\tilde{z}}}^3-1}d{\tilde{z}}\nonumber \\= & {} 2\lambda \mathcal {M}(\alpha ,\gamma ,z), \end{aligned}$$
(33)

where \(\mathcal {M}(\alpha ,\gamma ,z)\) is the function of \(\alpha \) and \(\gamma \) as well as z and can be given in the explicit form by analytical integration. Integrating further the above equation with the condition \(\chi (1)=0\), the function \(\chi (z)\) is derived as

$$\begin{aligned} \chi (z)=2\lambda \int ^{{\tilde{z}}=1}_{{\tilde{z}}=z} \frac{\mathcal {M}(\alpha ,\gamma ,{\tilde{z}})}{ 48 \gamma {\tilde{z}}^6-1 }d{\tilde{z}}=2\lambda \mathcal {N}(\alpha ,\gamma ,z), \end{aligned}$$
(34)

where \(\mathcal {N}(\alpha ,\gamma ,z)\) depends on the parameters \(\alpha \) and \(\gamma \) as well as the variable z, and its value can be obtained by numerical integration. Considering Eqs. (21) and (30) as well as (34), the condensate can be expressed as

$$\begin{aligned} \frac{\langle {\hat{J}}_x \rangle }{r_+^{\Delta +1}}=\frac{1}{\sqrt{2\mathcal {N}(\alpha ,\gamma ,0)}} \sqrt{\frac{T_c}{T}}\sqrt{1-\frac{T}{T_c}} \end{aligned}$$
(35)

Obviously, the condensate has a square root behavior near the critical temperature, which is consistent with the numerical results, especially, the grand potential and also indicates a second-order phase transition at the critical point expected from the mean-field theory.

To compare the behavior of condensate for the analytical results with the one of the numerical results more in detail, we further process Eq. (35) as

$$\begin{aligned} \frac{\langle {\hat{J}}_x \rangle ^{\frac{2}{5}}}{T_c}= & {} \frac{4\pi }{3}\frac{1}{(2\mathcal {N} (\alpha ,\gamma ,0))^\frac{1}{5}}\left( 1-\frac{T}{T_c}\right) ^{\frac{1}{5}}\nonumber \\= & {} \mathcal {C}(\alpha ,\gamma )\left( 1-\frac{T}{T_c}\right) ^{\frac{1}{5}}, \end{aligned}$$
(36)

where we have considered \(\Delta =\frac{3}{2}\) and the approximation \(T\approx T_c\). After some calculation, we have \(\mathcal {C}(0.70978,-\frac{1}{50})=8.07502\), \(\mathcal {C}(0.70032,-\frac{1}{100})=7.93396\), \(\mathcal {C}(0.67143,0)=7.5889\), \(\mathcal {C}(0.61583,\frac{1}{100})=7.03228\), \(\mathcal {C}(0.48781,\frac{1}{50})=6.03606\). It follows that the vector condensate increases faster with the decreasing \(C^2F^2\) parameter \(\gamma \), which is again consistent with the behavior of the condensate that the stable value decreases with the improving \(C^2F^2\) parameter \(\gamma \) in Fig. 1 and thus suggests that the analytical S–L method is still powerful for the holographic superconductor model with high derivative term [48, 67].

On the other hand, if we work in the canonical ensemble [19, 20, 48], we should impose the boundary condition \(\phi '(0)=-\frac{\rho }{r_+}\) with Eq. (21) replaced by \(\lambda =\frac{\rho }{r_{+c}^2}\). Meanwhile, the function on the right hand of Eq. (20) is corrected as \(\xi _1(z)=48 (1-z^7)/7\), \(\xi _2(z)=2304 (1-z^{13})/13\), \(\xi _3(z)=110592 (1-z^{19})/19\), \(\xi _4(z)=5308416 (1-z^{25})/25\), and Eq. (28) should be replaced by \(T_{c} = \frac{3}{4\pi \sqrt{\lambda }}\sqrt{\rho }\). We also calculate the critical temperature in the canonical ensemble for some special value of \(\gamma \), such as, \(T_{ca}=0.0912\sqrt{\rho }\) for \(\gamma =-\frac{1}{50}\), \(T_{ca}=0.0938\sqrt{\rho }\) for \(\gamma =-\frac{1}{100}\), \(T_{ca}=0.1124\sqrt{\rho }\) for \(\gamma =\frac{1}{100}\) and \(T_{ca}=0.1363\sqrt{\rho }\) for \(\gamma =\frac{1}{50}\). It follows that in the canonical ensemble the increasing \(C^2F^2\) parameter \(\gamma \) still enhances the conductor/superconductor phase transition. In particular, as \(\gamma =0\), i.e., the standard AdS case, we have \(T_{ca}=0.1006\sqrt{\rho }\) which is consistent with the result in Refs. [50, 53, 63].

3 Conclusions and discussions

In the present paper, we have realized the holographic p-wave conductor/superconductor model with 6 derivative term (\(C^2F^2\)) in the four-dimensional Schwarzschild-AdS black hole. We mainly studied the influences of the \(C^2F^2\) parameter \(\gamma \) in the range \(-\frac{1}{50}\le \gamma \le \frac{1}{50}\) on the superconductor model by both numerical and analytical methods. Main results are summarized as follows.

Firstly, for all values of the \(C^2F^2\) parameter \(\gamma \), there always exists a critical temperature below which the vector hair appears. From the condensate as a function of the temperature, we found the system suffers from a second-order phase transition at the critical point, which is upheld by the comparison between the grand potential in the normal state and hairy state with each other. Meanwhile, the critical temperature increases with the improving \(C^2F^2\) parameter \(\gamma \), which suggests that the larger \(C^2F^2\) parameter enhances the superconductor phase transition. In addition, at the low temperature, such as \(\frac{T}{T_c}\approx \frac{1}{10}\), the condensate saturates a stable value which decreases with the increasing \(C^2F^2\) parameter \(\gamma \). To backup the numerical results, we reconstructed the p-wave superconductor model by the S-L method in the grand canonical ensemble which seems to be not appeared in the previous work and found that both the critical temperature and the critical behavior of the vector condensate agree well with the numerical ones, especially, the critical exponent of the condensate is always \(\frac{1}{2}\) suggesting the second-order phase transition at the critical point [19,20,21, 33].

Secondly, at the critical temperature(i.e., \(\frac{T}{T_c}\approx 1\)), compared with the horizontal line of the real part of the conductivity corresponding to \(\gamma =0\), the real part of conductivity with \(\gamma =-\frac{1}{50}\) is promoted near the zero frequency and suppressed at the intermediate frequency and thus displays a Drude-like peak, which is similar to the case in Refs. [45, 46]. It is worth noting that the formation mechanism of the present Drude-like peak is different from the one for the p-wave case in the BTZ black hole, where the conductivity decreases with the increasing frequency [64]. However, for the case of \(\gamma =\frac{1}{50}\), the real part of conductivity is suppressed near the zero frequency and promoted at the intermediate frequency and thus produces an obviously pronounced peak at the intermediate frequency, which is also similar to the conductivity in Refs. [45, 46]. At the low temperature such as \(\frac{T}{T_c}\approx \frac{1}{10}\), for any value of \(C^2F^2\) parameter \(\gamma \), we can always observe the infinite DC conductivity expected from the superconductor, which corresponds to the pole of the imaginal part of conductivity. What is more, we obtained an obvious energy gap at the intermediate frequency from the minimum of the imaginal part of conductivity. It was found that the ratio of the energy gap to the critical temperature(\(\frac{\omega _g}{T_c}\)) decreases with the increasing \(\gamma \), which is consistent with the phase diagram of the critical temperature versus the \(C^2F^2\) parameter \(\gamma \). In addition, the running range \(\frac{\omega _g}{T_c}\in [4.582,9.172]\) (much) larger than the BCS value (3.54) reflects the strong interaction for the current superconductor model.

In current paper we have only worked in the probe limit. Although this probe limit can reveal some main properties of superconductor, it was shown that new phases such as zero-order phase transition and the retrograde phase can emerge once the backreaction is taken into account [16, 58, 59]. Therefore, it is interesting to build the superconductor model by including the backreaction from the \(C^2F^2\) correction to the AdS metric via both numerical shooting method [17, 22, 31, 40] and analytical S-L method [21, 38, 64, 68, 69]. Meanwhile, as we all know, in the high critical temperature phase diagram, an insulator phase is located close to the superconducting phase [14]. Therefore, it is meaningful to construct the insulator/superconductor phase transition to see whether there are some new features compared with the present conductor/superconductor model.