Abstract
We study the thermodynamic properties of asymmetric quark matter and large mass quark stars within the confined-isospin-density-dependent-quark-mass model. We find that the quark matter symmetry energy should be very large in order to describe the recent discovered heavy compact stars PSR J0348+0432 (\(\text {2.01}\pm \text {0.04}M_{\odot }\)), MSP J0740+6620 (\(\text {2.14}\pm ^\text {0.10}_\text {0.09}M_{\odot }\) of 68.3\(\%\) credibility interval and \(\text {2.14}\pm ^\text {0.20}_\text {0.18}M_{\odot }\) of 95.4\(\%\) credibility interval) and PSR J2215+5135 (2.27\(\pm ^\text {0.10}_\text {0.09}M_{\odot }\)) as QSs. The tidal deformability \(\Lambda _{1.4}\) of the QSs is also investigated in this work, and the result indicates that \(\Lambda _{1.4}\) may depend on the isospin effects and the strength / orientation distribution of the magnetic fields inside the quark stars.
Similar content being viewed by others
1 Introduction
Neutron stars (NSs) provide the astrophysical testing base to obtain the thermodynamic properties of strongly interacting matter at large baryon density and low (or even zero) temperature [1,2,3,4]. From lots of theoretical studies, NSs could be converted to hybrid stars or strange quark stars (QSs), and the possible existence of QSs is still one of the most important fields for modern nuclear physics and astrophysics [5,6,7,8,9,10,11]. These stars are usually made up of deconfined absolutely stable \(u,~d~\text {and}~s\) quarks with leptons in \(\beta -\)equilibrium condition, which is defined as strange quark matter (SQM) [7, 8, 12,13,14,15,16], and the thermodynamic properties of SQM is of great significance in determining the information of star mass and radius. Recently, the large star mass of PSR J1614-2230 has been precisely measured as \(1.97\pm 0.04~M_{\odot }\) [17] by using Shapiro delay, while a new heavier pulsar PSR J0348+0432 with a mass of \(2.01\pm 0.04~M_{\odot }\) [18] was discovered in 2013. By fitting the radial velocity lines and the three-band light curves in the irradiated compact stars model, a more massive compact star PSR J 2215+5135 has been detected, whose star mass is \(2.27^{+0.17}_{-0.15}~M_{\odot }\) [19]. In Ref. [20], the MSR J0740+6620 (\(\text {2.14}\pm ^\text {0.10}_\text {0.09}M_{\odot }\) with 68.3\(\%\) credibility interval and \(\text {2.14}\pm ^\text {0.20}_\text {0.18}M_{\odot }\) with 95.4\(\%\) credibility interval) is considered as the most massive precisely observed pulsar by using the data of relativistic Shapiro delay with the Green Bank Telescope. The heavy star observations above may put new strict constraints on the equation of state (EOS) and the isospin effects of the strong interactions in nuclear matter inside the compact stars. Since the EOS of strange quark matter is usually not stiff due to the addition of s quark and the asymptotic freedom feature of QCD at large baryon density region, most of quark matter models predict relatively smaller maximum mass of QSs. The large star mass from PSR J1614-2230, PSR J0348+0432, and PSR J2215+5135 could rule out lots of conventional phenomenological models for quark matter, whereas there exist some other models which can still provide heavy quark stars [21,22,23,24,25,26,27,28,29,30]. These models indicate that the isospin interaction in star matter should be strong enough in order to describe two solar mass compact stars as QSs.
In recent works, the gravitational wave (GW) signal GW170817 from a binary compact star system has been directly detected and declared by the LIGO-Virgo collaboration [31]. Lots of constraints on the thermodynamic properties of the strong interaction matter in compact stars have been calculated based on the observation [32,33,34,35,36,37,38,39,40,41]. In Ref. [31], the LIGO-Virgo collaboration focuses on the tidal deformability of the compact stars (which can also constrain the equation of state (EOS) of strongly interacting matter in stars) and sets an upper limit as \(\Lambda _{1.4}<800\) for the low-spin priors of the 1.4 solar mass pulsars. In subsequent works [34, 38, 39, 42,43,44,45,46], new constraints on the properties of the symmetry energy and equation of state for nuclear matter have been proposed. In the work [47], the new limitations for \(\tilde{\Lambda }\) was calculated as (0, 630) for large spin pulsar, \(300^{+420}_{-230}\) by considering the largest posterior density interval, and \(\Lambda _{1.4}=190^{+390}_{-120}\) by using the \(\Lambda m^5\) linear expansion around 1.4 \(M_{\odot }\) [34, 48]. For hybrid stars and quark stars, the GW observation of tidal deformability can also be proved to constrain the properties of the EOS, and the results indicate that GW170817 might have the possibility of producing from the binary quark hybrid star merger [37, 49, 50].
In Refs. [51,52,53], large magnetic field strength of \(B\sim 10^{14}\) G has been calculated at the surface of compact stars, and the magnetic field strength may reach as large as \(B=10^{18}\) G\(\sim \) \(10^{20}\) G in the core of magnetars [54,55,56]. The \(\mathcal {O}(3)\) symmetry can be broken in such large magnetic fields, and the pressure density of the strongly interacting matter inside the magnetars then becomes anisotropic [55,56,57,58,59]. However, whether introducing the strong magnetic fields into the calculations of the quark star physics can enhance or reduce the maximum star mass is still controversial in many works [60,61,62,63,64,65,66,67,68,69,70,71]. In the present work, we investigate the properties of the quark stars by using the density-dependent magnetic field profile [60, 61, 72] and two extreme cases for the magnetic field orientation distribution inside the quark stars in order to find out the relation between the maximum mass of magnetized QSs and the tidal deformability of the magnetars (\(\Lambda _{1.4}\)) under strong magnetic fields.
2 The confined isospin- and density-dependent mass model
There exist large number of phenomenological models to calculate the properties of SQM, [9,10,11, 73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101]. In this work, we use the confined isospin- and density-dependent mass (CIDDM) model [102,103,104] to explore the the properties of the tidal deformability and the quark star matter. The equivalent quark mass for CIDDM model is expressed as
where we define the bare quark mass as \(m_{q0}\), z is the scaling parameter of quark mass, D is determined by stability condition for SQM, \(n_B\) means the baryon number density defined by \(n_B=(n_u+n_d+n_s)/3\), and \(D_I\), \(\alpha \) and \(\beta \) can be adjusted to determine the isospin-dependent strong interaction in quark matter. The isospin asymmetry is defined as \(\delta = 3\frac{n_d-n_u}{n_d+n_u}\) and \(\tau _q \) is the isospin quantum number for quarks [105,106,107,108].
Since the isovector properties of quark matter are of significance to explore the EOS of SQM and understand the isospin properties of quark stars, quark matter symmetry energy are proposed to obtain the isospin effects inside the asymmetric quark matter [44, 45, 104]. Large quark matter symmetry energy can greatly reduce difference between the fraction of u and d quarks, which can further influence the equation of state of the star matter. The quark matter symmetry energy Eq. (2) at zero temperature can be expressed as
where E is the energy per baryon number for isospin asymmetric quark matter, and one can obtain a similar definition of the symmetry energy for nuclear matter in Refs. [109,110,111].
The energy density of quark matter at zero temperature can be written as
where \(\mu \) stands for the chemical potential for quarks, and the pressure of SQM at zero temperature can be given by
where \(f(x)=\frac{3}{2x^3}\left[ x\sqrt{(x^2+1)}+\ln {(x+\sqrt{x^2+1}})\right] \) and \(\nu _i\) is the Fermi momentum of the i-th particle.
For strange quark matter under strong magnetic fields, the spatial \(\mathcal {O}(3) \) symmetry will be broken. In the mean time the pressure becomes anisotropic and then splits into the transverse pressure \(P_\perp \) (perpendicular to B) and the longitudinal pressure \(P_\parallel \) (parallel to B). The anisotropic pressures for the magnetized fermion system can be calculated as [55, 56]
where M is the system magnetization, and one can find that the longitudinal pressure \(P_\parallel \) can satisfy the Hugenholtz-Van Hove (HVH) theorem [112].
To see more details about the CIDDM model, the readers are referred to Refs. [72, 102].
3 Results and discussions
3.1 Equation of state under constant magnetic fields
In this work, the bare mass of quarks and leptons we set is \(m_{u0}=m_{d0}=5.5\) MeV, \(m_{s0}=80\) MeV, \(m_e=0.511\) MeV and \(m_{\mu }=105.7\) MeV. The parameter sets we used are: (1) DI-85 with \(D_I=85,~D=22.922~\text {MeV}~\text {fm}^{3z}~\text {and}~z=1.8\), (2) DI-245 with \(D_I=245,~D=17.797~\text {MeV}~\text {fm}^{3z}~\text {and}~z=1.8\), and (3) DI-400 with \(D_I=400,~D=15.96~\text {MeV}~\text {fm}^{3z}~\text {and}~z=1.8\). In order to simulate the similar density dependence of the free fermi gas symmetry energy [102], we use \(\alpha =0.7\) and \(\beta =0.1~\hbox {fm}^3\) in all the three cases. The parameter D for DI-80, DI-245 and DI-400 is adjusted to satisfy the absolute stability of strange quark matter. As we will show later, the first parameter set is able to describe the PSR J0348+ 0432 with the mass of \(2.01\pm 0.04M_{\odot }\) [18] as QSs within CIDDM model [102], while the second parameter set can be used to describe the recently discovered massive pulsar MSR J0740+6620 (\(\text {2.14}\pm ^\text {0.10}_\text {0.09}M_{\odot }\) of 68.3\(\%\) credibility interval and \(\text {2.14}\pm ^\text {0.20}_\text {0.18}M_{\odot }\) of 95.4\(\%\) credibility interval) [20] as QSs. Using the third parameter set, we can describe PSR J2215+5135 with the mass of 2.27\(\pm ^\text {0.10}_\text {0.09}M_{\odot }\) [19] as QSs in Fig. 3.
From Fig. 1, we calculate the symmetry energy as functions of baryon density with DI-85, DI-245 and DI-400. One can find that the symmetry energy increases sharply (especially for DI-400) with the increment of the baryon number density for each parameter set, and one can also see that the value of the symmetry energy considerably increases with \(D_I\) in Fig. 1 at a certain baryon number density (the values of the quark matter symmetry energy with DI-85, DI-245 and DI-400 are calculated as 70.8 MeV, 352.6 MeV and 883.8 MeV at \(n_{B}=1.5~\text {fm}^{-3}\)). For the parameter adjustment, the isospin dependence intensity parameters \(D_I\) listed are the minimum \(D_I\) value we searched for so as to support the three massive compact star cases above as QSs, and this result implies that large quark star mass may put strong constraints on the isovector properties of strange quark matter.
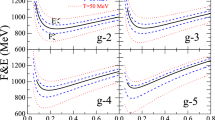
In Fig. 2, we investigate the properties of the equation of state for strange quark matter with DI-85, DI-245 and DI-400 at \(B=0,~2\times 10^{18}~G~\text {and} ~3\times 10^{18}~G\). We should first point out that all the parameter sets in Fig. 2 can guarantee the the absolutely stable condition of strange quark matter from Farhi and Jaffe [9]. One can find in Fig. 2 that the minimum value of the energy per baryon number becomes smaller when \(D_I\) increases, while the energy per baryon increases with the constant magnetic field B. From the numerical results we can provide that the baryon density at the minimum energy per baryon number is exactly the density of zero-pressure point, which is consistent with the thermodynamic self-consistency. We also note that the zero-pressure point density decreases with the increment of \(D_I\), while the zero-pressure point density increases when the magnetic field increases. The pressure for SQM at zero magnetic field increases from 289.9 MeV to 298.9 MeV with \(D_I\) increasing from 85 to 400, which indicates that the stiffness of the EOS increases with the isospin-dependence intensity parameter \(D_I\), which implies that large isospin effects can significantly influence the EOS of strange quark matter.
In Fig. 3, we calculate the mass and radius at different central density of QSs at zero magnetic field with DI-85, DI-245 and DI-400. Using the results of the EOS of SQM in Fig. 2, one can describe the large-mass pulsar PSR J0348+ 0432 with the mass of 2.01±0.04\(M_{\odot }\) [18] as QSs within CIDDM model [102] with DI-85. Since the EOS of SQM becomes stiffer with \(D_I\) (the isospin effect), we can also obtain the recently precisely discovered heaviest compact star MSR J0740+6620 as QSs with DI-245. As \(D_I\) increasing to \(D_I=400\), the isospin effect gets larger and the maximum mass of the quark star with DI-400 increases to 2.27 solar mass, which is able to describe PSR J2215+5135. The tidal deformability at 1.4 \(M_{\odot }\) (\(\Lambda _{1.4}\)) for DI-85, DI-245 and DI-400 is calculated as 241.6, 345.9 and 408.89, which indicates that we can describe all the three large mass compact stars as quark stars at zero temperature by considering the already mentioned constraints of the tidal deformability \(\Lambda _{1.4}<800\) and \(\Lambda _{1.4}=190^{+390}_{-120}\). This result indicates that both the maximum mass and \(\Lambda _{1.4}\) of QSs increase when the isospin interaction intensity parameter \(D_I\) increases within CIDDM model at zero temperature and zero magnetic field.
3.2 Quark stars under density dependent magnetic fields
Since strong magnetic field strength has been estimated as \(B\approx ~10^{14}\) G at the surface of compact stars, we use the density-dependent magnetic field profile [60,61,62,63,64,65, 72] inside the QSs in the present work in order to provide the magnetic field strength distribution inside the stars (the magnetic fields strength is generally believed to be weak at surface and strong in the core).
Here we use the “fast-B” profile from the Ref. [72]: the parameter \(B_{surf} = 10^{15}\)G stands for the magnetic field at the star surface, \(n_0 = 0.16\) fm\(^{-3}\) means the normal density of the nuclear matter, \(B_0\) is a free magnetic field parameter, and \(\beta _0=0.001 \) and \(\gamma =3 \) are two dimensionless parameters which are used to provide a strong density dependent magnetic field strength distribution from core to the surface. In Ref. [72], due to the lack of the empirical information about the magnetic field orientation distribution of magnetars, the authors has assumed two extremely special magnetic field orientation distribution cases: one is defined as the “radial orientation” case, which is assumed as that the magnetic fields inside the star are along the radial direction, while the other is considered as “transverse orientation”, which is assumed as that the magnetic fields are perpendicular to the radius but oriented randomly in the plane that is perpendicular to the radius. Using the two cases of the orientation distribution of B, one can consider the pressure density inside the quark stars being spherically symmetric.
Then employing this two extreme orientation cases of B, one can use Tolman-Oppenheimer-Volkoff (TOV) equations [113] to calculate the mass-radius relation of magnetars.
In Fig. 4, we calculate the maximum mass of QSs using the transverse and radial orientations cases as a function of \(B_0\) with the fast B-profile with DI-245. One can see from Fig. 4 that the maximum mass of static QSs with the radial (transverse) orientation is 2.14 solar mass at zero magnetic fields and then decreases (increases) to 2.03 \(M_{\odot }\) (2.23 \(M_{\odot }\)) at \(B_0=7\times 10^{18}\) G. The normalized mass asymmetry \(\delta _m=\frac{M_{\perp }-M_{||}}{(M_{\perp }+M_{||})/2}\) is calculated as \(9.4\%\) at \(B_0=7\times 10^{18}\) G. One can obtain that the maximum mass of quark stars will be influenced obviously by the magnetic field orientation cases when the magnetic field \(B_0\) becomes larger than \(10^{18}\) G. The result implies that the two extreme cases can also set the star-mass-region (as the upper and lower limits of the region) which may contain all the cases of the maximum mass of stars considering other nonspherical orientation distribution with the corresponding magnetic field strength.
As we have mentioned, the observation of tidal effects in binary compact star system can provide significant information about the thermodynamic properties and EOS inside the star matter because of the tidal deformation being determined by the internal structure of the compact stars. In Fig. 5, we calculate the tidal deformability at 1.4 solar mass (\(\Lambda _{1.4}\)) as functions of \(B_0\) with the fast B-profile within CIDDM model with DI-245. One can find the tidal deformability increases with \(B_0\) with the transverse orientation case while decreasing with the magnetic field with the radial orientation case. And the value of \(\Lambda _{1.4}\) of QSs with the radial (transverse) orientation is 345.9 at zero magnetic fields and can further reach 304.7 (402.1) at \(B_0=7\times 10^{18}\) G, which obviously satisfies the constraints in tidal deformability \(\Lambda _{1.4}<800\) and \(\Lambda _{1.4}=190^{+390}_{-120}\). These results show that the tidal deformability of the magnetars (\(\Lambda _{1.4}\)) increases / decreases with the magnetic fields when the magnetic field orientation is considered as transverse / radial orientation inside the QSs, which implies that the tidal deformability of the magnetars (\(\Lambda _{1.4}\)) may also depend on not only the isospin interaction strength inside the star matter but also the strength and the orientation distribution of the magnetic fields inside the QSs.
We also study the high-density limit of the EOS within CIDDM model in Fig. 6. Shown in the left panel of Fig. 6 is the ratio of the pressure with DI-245 to the pressure for the free fermi gas at zero magnetic field as a function of baryon density, and one can find that the ratio nearly reaches 1 at very large baryon density. For the right panel in Fig. 6, we calculate the sound velocity square within DI-245 at zero magnetic field as a function of the energy density within CIDDM, and one can also see that the sound velocity square decreases to 1/3 when the energy density increases to 10,000 MeV. The results indicate that the quark-quark interactions among the quark matter within CIDDM model almost decrease to zero at large baryon density and high energy density, which satisfies the feature of the asymptotic freedom for quarks.
4 Conclusions
In this work, we have studied the properties of SQM and QSs within the CIDDM model. The quark matter symmetry energy and the stability of SQM have been explored. We found that the stiffness of the EOS of SQM increases with the isospin effect intensity parameter \(D_I\) within CIDDM model, and the quark matter symmetry energy should be large enough so as to describe the recent discovered heavy compact stars (PSR J0348+ 0432, MSR J0740+6620 and PSR J2215+5135) as QSs. The calculation results also indicate that both the maximum mass and \(\Lambda _{1.4}\) of QSs increase when the isospin dependence in the equivalent quark mass becomes stronger within CIDDM model at zero temperature and zero magnetic field.
We have furthered studied the maximum mass of magnetars within the CIDDM model by using the density-dependent magnetic field inside the stars. We have found that the maximum mass of static QSs increases with \(B_0\) for the transverse orientation case while decreasing with \(B_0\) for the radial orientation, and the tidal deformability of the magnetars (\(\Lambda _{1.4}\)) increases / decreases with the magnetic fields when the magnetic field orientation is considered as transverse / radial orientation inside the QSs.
Therefore, our results have shown that considering isospin dependence in equivalent quark mass within CIDDM model can significantly influence the values of quark matter symmetry energy, properties of the equation of state in SQM, and the maximum mass and the tidal deformability of static QSs. The maximum mass of magnetized QSs and the tidal deformability of the magnetars (\(\Lambda _{1.4}\)) may depend on both the strength distribution and the orientation of the magnetic fields inside the QSs.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and no experimental data has been listed.]
References
N.K. Glendenning, Compact Stars, 2nd edn. (Spinger, New York, 2000)
F. Weber, Pulsars as Astrophyical Laboratories for Nuclear and Particle Physics (IOP Publishing Ltd, London, UK, 1999)
J.M. Lattimer, M. Prakash, Science 304, 536 (2004)
A.W. Steiner, M. Prakash, J.M. Lattimer, P.J. Ellis, Phys. Rep. 410, 325 (2005)
D. Ivanenko, D.F. Kurdgelaidze, Lett. Nuovo Cimento 2, 13 (1969)
N. Itoh, Prog. Theor. Phys. 44, 291 (1970)
A.R. Bodmer, Phys. Rev. D 4, 1601 (1971)
E. Witten, Phys. Rev. D 30, 272 (1984)
E. Farhi, R.L. Jaffe, Phys. Rev. D 30, 2379 (1984)
C. Alcock, E. Farhi, A. Olinto, Astrophy. J. 310, 261 (1986)
F. Weber, Prog. Part. Nucl. Phys. 54, 193 (2005)
I. Bombaci, I. Parenti, I. Vidana, Astrophy. J. 614, 314 (2004)
J. Staff, R. Ouyed, M. Bagchi, Astrophy. J. 667, 340 (2007)
M. Herzog, F.K. Röpke, Phys. Rev. D 84, 083002 (2011)
M.A. Stephanov, K. Rajagopal, E.V. Shuryak, Phys. Rev. Lett. 81, 4816 (1998)
H. Terazawa, INS-Report 336, Univ. of Tokyo, (1979)
P. Demorest, T. Pennucci, S. Ransom, M. Roberts, J. Hessels, Nature 467, 1081 (2010)
J. Antoniadis et al., Science 340, 6131 (2013)
M. Linares, T. Shahbaz, J. Casares, APJ 859, 54 (2018)
H. Thankful Cromartie et al., arXiv:1904.06759 (2019), Nature Astronomy Letter (2019)
M. Alford, S. Reddy, Phys. Rev. D 67, 074024 (2003)
M. Alford, P. Jotwani, C. Kouvaris, J. Kundu, K. Rajagopal, Phys. Rev. D 71, 114011 (2005)
M. Baldo, Phys. Lett. B 562, 153 (2003)
N.D. Ippolito, M. Ruggieri, D.H. Rischke, A. Sedrakian, F. Weber, Phys. Rev. D 77, 023004 (2008)
X.Y. Lai, R.X. Xu, Res. Astron. Astrophys. 11, 687 (2011)
M.G.B. de Avellar, J.E. Horvath, L. Paulucci, Phys. Rev. D 84, 043004 (2011)
L. Bonanno, A. Sedrakian, A&A 539, A16 (2012)
P.C. Chu et al., Phys. Rev. D 94, 123014 (2016)
P.C. Chu et al., Eur. Phys. J. C 77, 512 (2017a)
P.C. Chu et al., J. Phys. G: Nucl. Part. Phys. 47, 085201 (2020)
B.P. Abbott et al., Phys. Rev. Lett. 119, 161101 (2017)
Luciano Rezzolla, Elias R. Most, Lukas R. Weih, Astrophys. J. Lett. 852(2), L25 (2018)
Elias R. Most et al., Phys. Rev. Lett. 120, 261103 (2018)
Ying Zhou, Lie-Wen Chen, Zhen Zhang, Phys. Rev. D 99, 121301(R) (2019)
A. Bauswein, O. Just, H.-T. Janka, N. Stergioulas, Astrophys. J. Lett. 850, L34 (2017)
B. Margalit, B.D. Metzger, Astrophys. J. Lett. 850, L19 (2017)
E. Zhou, X. Zhou, A. Li, Phys. Rev. D 97, 083015 (2018)
F.J. Fattoyev, J. Piekarewicz, C.J. Horowitz, Phys. Rev. Lett. 120, 172702 (2018)
E. Annala, T. Gorda, A. Kurkela, A. Vuorinen, Phys. Rev. Lett. 120, 172703 (2018)
D. Radice, A. Perego, F. Zappa, S. Bernuzzi, Astro- phys. J. Lett. 852, L29 (2018)
M. Ruiz, S.L. Shapiro, A. Tsokaros, Phys. Rev. D 97, 021501(R) (2018)
J.-E. Christian, A. Zacchi, J. Schaffner-Bielich, arXiv:1809.03333 (2018)
G. Montana, L. Tolos, M. Hanauske, L. Rezzolla, arXiv:1811.10929 (2018)
P.C. Chu et al., Phys. Rev. C 99, 035802 (2019)
P.C. Chu et al., Phys. Rev. D 100, 103012 (2019)
N.B. Zhang, B.A. Li, arXiv:1904.10998 (2019)
The LIGO Scientific Collaboration, the Virgo Collaboration, B. P. Abbott et al., Phys. Rev. X 9, 011001 (2019)
B.P. Abbott et al., Phys. Rev. Lett. 121, 161101 (2018)
R. Nandi, P. Char, Astrophys. J. 857, 12 (2018)
V. Paschalidis, K. Yagi, D. Alvarez-Castillo, D. B. Blaschke, A. Sedrakian, arXiv:1712.00451 (2017)
L. Woltjer, Astrophys. J. 140, 1309 (1964)
T.A. Mihara, Nature (London) 346, 250 (1990)
G. Chanmugam, Annu. Rev. Astron. Astrophys. 30, 143 (1992)
D. Lai, S.L. Shapiro, Astrophys. J. 383, 745 (1991)
E.J. Ferrer, V. de la Incera, J.P. Keith, I. Portillo, P.L. Springsteen, Phys. Rev. C 82, 065802 (2010)
E.J. Ferrer, V. de la Incera, Lect. Notes Phys. 871, 399 (2013)
A.A. Isayev, J. Yang, Phys. Rev. C 84, 065802 (2011)
A.A. Isayev, J. Yang, Phys. lett. B 707, 163 (2012)
A.A. Isayev, J. Yang, J. Phys. G 40, 035105 (2013)
D. Bandyopadhyay, S. Chakrabarty, S. Pal, Phys. Rev. Lett. 79, 2176 (1997)
D. Bandyopadhyay, S. Pal, S. Chakrabarty, J. Phys. G 24, 1647 (1998)
D.P. Menezes, M.Benghi Pinto, S.S. Avancini, C. Providência, Phys. Rev. C 79, 035807 (2009)
D.P. Menezes, M.Benghi Pinto, S.S. Avancini, C. Providência, Phys. Rev. C 80, 065805 (2009)
C.Y. Ryu, K.S. Kim, M.K. Cheoun, Phys. Rev. C 82, 025804 (2010)
C.Y. Ryu, M.K. Cheoun, T. Kajino, T. Maruyama, G.J. Mathews, Astropart. Phys. 38, 25 (2012)
A. Broderick, M. Prakash, J.M. Lattimer, Astrophys. J. 537, 351 (2000)
C.Y. Cardall, M. Prakash, J.M. Lattimer, Astrophys. J. 554, 322 (2001)
L. Paulucci, E.J. Ferrer, V. de la Incera, J.E. Horvath, Phys. Rev. D 83, 043009 (2011)
V. Dexheimer, D.P. Menezes, M. Strickland, J. Phys. G 41, 015203 (2014)
R.H. Casali, L.B. Castro, D.P. Menezes, Phys. Rev. C 89, 015805 (2014)
J.X. Hou, G.X. Peng, C.J. Xia, J.F. Xu, arXiv:1403.1143, (2014)
P.C. Chu, L.W. Chen, X. Wang, Phys. Rev. D 90, 063013 (2014)
A. Chodos, R.L. Jaffe, K. Ohnson, C.B. Thorn, V.F. Weisskopf, Phys. Rev. D 9, 3471 (1974)
M. Alford, M. Braby, M. Paris, S. Reddy, Astrophy. J. 629, 969 (2005)
J.Y. Chao et al., Phys. Rev. D 88, 054009 (2013)
P.C. Chu et al., Phys. Rev. D 91, 023003 (2015)
P.C. Chu et al., Phys. Rev. D 93, 094032 (2016)
P.C. Chu et al., Phys. Rev. D 96, 083019 (2017)
P. Rehberg, S.P. Klevansky, J. Hüfner, Phys. Rev. C 53, 410 (1996)
M. Hanauske, L.M. Satarov, I.N. Mishustin, H. Stocker, W. Greiner, Phys. Rev. D 64, 043005 (2001)
S.B. Rüster, D.H. Rischke, Phys. Rev. D 69, 045011 (2004)
D.P. Menezes, C. Providencia, D.B. Melrose, J. Phys. G 32, 1081 (2006)
C.D. Roberts, A.G. Williams, Prog. Part. Nucl. Phys. 33, 477 (1994). and references therein
H.S. Zong, L. Chang, F.Y. Hou, W.M. Sun, Y.X. Liu, Phys. Rev. C 71, 015205 (2005)
S.X. Qin, L. Chang, H. Chen, Y.X. Liu, C.D. Roberts, Phys. Rev. Lett. 106, 172301 (2011)
B.A. Freedman, L.D. Mclerran, Phys. Rev. D 16, 1169 (1977)
E.S. Fraga, R.D. Pisarski, J. Schaffner-Bielich, Phys. Rev. D 63, 121702(R) (2001)
E.S. Fraga, P. Romatschke, Phys. Rev. D 71, 105014 (2005)
A. Kurkela, P. Romatschke, A. Vuorinen, Phys. Rev. D 81, 105021 (2010)
G.N. Fowler, S. Raha, R.M. Weiner, Z. Phys. C 9, 271 (1981)
S. Chakrabarty, S. Raha, B. Sinha, Phys. Lett. B 229, 112 (1989)
S. Chakrabarty, Phys. Rev. D 43, 627 (1991)
S. Chakrabarty, Phys. Rev. D 48, 1409 (1993)
S. Chakrabarty, Phys. Rev. D 54, 1306 (1996)
O.G. Benvenuto, G. Lugones, Phys. Rev. D 51, 1989 (1995)
G.X. Peng, H.C. Chiang, J.J. Yang, L. Li, B. Liu, Phys. Rev. C 61, 015201 (1999)
G.X. Peng, H.C. Chiang, B.S. Zou, P.Z. Ning, S.J. Luo, Phys. Rev. C 62, 025801 (2000)
G.X. Peng, A. Li, U. Lombardo, Phys. Rev. C 77, 065807 (2008)
A. Li, G.X. Peng, J.F. Lu, Research. Astron. Astrophys. 11, 482 (2011)
K. Schertler, C. Greiner, M.H. Thoma, Nucl. Phys. A 616, 659 (1997)
K. Schertler, C. Greiner, P.K. Sahu, M.H. Thoma, Nucl. Phys. A 637, 451 (1998)
P.C. Chu, L.W. Chen, Astrophys. J. 780, 135 (2014)
P.C. Chu et al., Phys. Lett. B 778, 447 (2018)
P.C. Chu, L.W. Chen, Phys. Rev. D 96, 103001 (2017)
M. Di Toro, A. Drago, T. Gaitanos, V. Greco, A. Lavagno, Nucl. Phys. A 775, 102 (2006)
G. Pagliara, J. Schaffner-Bielich, Phys. Rev. D 81, 094024 (2010)
M. Di Toro, V. Baran, M. Colonna, V. Greco, J. Phys. G 37, 083101 (2010)
G.Y. Shao, M. Colonna, M. Di Toro, B. Liu, F. Matera, Phys. Rev. D 85, 114017 (2012)
B.A. Li, L.W. Chen, C.M. Ko, Phys. Rept. 464, 113 (2008)
X.H. Li, B.J. Cai, L.W. Chen, R. Chen, B.A. Li, C. Xu, Phys. Lett. B 721, 101 (2013)
X.H. Li, W.J. Guo, B.A. Li, L.W. Chen, F.J. Fattoyev, W.G. Newton, Phys. Lett. B 743, 408 (2015)
N.M. Hugenholtz, L. Van Hove, Physica 24, 363 (1958)
J.R. Oppenheimer, G.M. Volkoff, Phys. Rev. 33, 374 (1939)
Acknowledgements
This work is supported by the NSFC under Grants No. 11975132, 11905302, 41702322, 11505100, 11804179 and No. 61772295, and the Shandong Provincial Natural Science Foundation, China ZR2019YQ01, ZR2016DB01, ZR2019PA018, ZR2015AQ007, and 2017GSF216010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
About this article
Cite this article
Chu, PC., Zhou, Y., Jiang, YY. et al. Quark star matter in heavy quark stars. Eur. Phys. J. C 81, 93 (2021). https://doi.org/10.1140/epjc/s10052-020-08800-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08800-3