1 Introduction

A meaningful and historic subject of the perturbative QCD, which has received considerable attention in the past few decades, is the study of the exclusive processes at large momentum transfer. The pioneer works in this area are performed by Efremov and Radyushkin [1] and, independently, Brodsky and Lepage [2]. They pointed out that the exclusive processes at large momentum transfer can be factorized into perturbatively calculable kernels and hadronic wave functions. Although there is general agreement that perturbative QCD is able to make reliable predictions for the exclusive processes in the large energy region [3], the applicability of perturbative QCD to these processes in the intermediate energy region has been developed in controversy. In the field of exclusive processes, two-photon collisions \(\gamma \gamma \rightarrow \pi ^+\pi ^-,K^+K^-\) [4,5,6,7,8] are the specially ones with the initial states simple and controllable and the strong interactions only in the final states. These characteristics make the processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-,K^+K^-\) be a good testing ground for our understanding of the perturbative and nonperturbative structure of QCD.

In the perturbative QCD approach based on the collinear factorization, the first investigation of the processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-, K^+K^-\) was carried out by Brodsky and Lepage [9]. At leading-twist leading-order level, they gave detailed calculations of the helicity amplitudes of these processes and presented the known relation between the differential cross section and the time-like electromagnetic form factor:

$$\begin{aligned} \frac{\mathrm {d}\sigma (\gamma \gamma \rightarrow M^{+}M^{-})}{\mathrm {d}|\cos \theta |}\approx \frac{8\pi \alpha ^{2}}{Q^{2}}\frac{|F_{M}(Q^{2})|^{2}}{\sin ^{4}\theta }. \end{aligned}$$
(1)

Several years later, Nižić [10] performed the leading-twist next-to-leading-order perturbative QCD calculations for these processes. In Refs. [10, 11], it was found that both the leading-order and next-to-leading-order perturbative QCD predictions are almost an order of magnitude smaller than the experiment data [12,13,14,15,16] in the intermediate energy region. Motivated by the calculation of the pion electromagnetic form factor [17] in which the nonleading twist contribution becomes the dominant one in a few GeV region, Gorsky [18] investigated the two-photon process \(\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}\) with the higher-twist corrections. It was pointed out that the two-parton twist-3 contributions are logarithmically larger than the leading-twist contributions in the intermediate energy region due to the chiral enhancement effects. And this conclusion had also been confirmed in Ref. [19] with the Brodsky–Huang–Lepage (BHL) prescription [20]. But in a few GeV region, the predicted cross sections with higher-twist corrections [18, 19] are several times larger than their experimental measurements [12,13,14,15,16].

As it is known that the higher-power effects from the intrinsic transverse momentum play a crucial role in the pion electromagnetic form factor at the scale of few GeV [21, 22], one may expect that the same situation can also be found in the two-photon processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-, K^+K^-\). Based on the \(k_{T}\) factorization theorem [21, 23] in which the transverse momentum dependence was retained, the leading-twist perturbative QCD predictions for the cross sections of these two-photon processes were obtained in Refs. [24,25,26,27,28,29]. From the analysis of the differential cross sections obtained in both perturbative QCD and QCD sum rule, the conclusion that the transition from nonperturbative to perturbative QCD in \(\gamma \gamma \rightarrow \pi ^+\pi ^-, K^+K^-\) occurs at \(Q\approx 2~\mathrm {GeV}\) was drawn in Refs. [25, 26, 29]. However, the numerical results in Refs. [27, 28] show that the twist-2 cross sections of the \(\gamma \gamma \rightarrow \pi ^+\pi ^-, K^+K^-\) in the \(k_{T}\) factorization are still much smaller than the experiment data in the intermediate energy region.

To consider the higher-twist effects for the processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-, K^+K^-\) in \(k_{T}\) factorization would be a natural next step, and seems necessary because the higher-twist effects and the higher-power effects from the transverse momentum become important simultaneously in intermediate energy region. Compared with the previous calculations in collinear factorization [18, 19], the higher-twist calculations in \(k_{T}\) factorization have several major improvements: Firstly, both the transverse momentum dependence of hadronic wave functions and that of hard kernels are included. The transverse momentum dependence of the hard kernel regularizes the end-point singularities of the internal propagators. While the transverse momentum dependence of the wave function makes a sizable suppression to the perturbative QCD contributions, and cannot be ignored as pointed out in Ref. [22], especially in the few GeV region. Secondly, the corrections from the Sudakov resummation [21] substantially suppress the nonperturbative contributions from both the soft end-point regions and the large-b regions. Moreover, the corrections from the threshold resummation [30] suppress the nonperturbative contributions from the end-point regions further and eliminate the end-point singularity without a artificial cut-off [18] or the BHL prescription [20] in the twist-3 calculations. Thirdly, the scales of the coupling constant \(\alpha _s\) are chosen to be momentum-fraction dependent in order to avoid large logarithms from higher-order perturbative QCD corrections. All of the aforementioned improvements make the perturbative calculation become more self-consistent, even for momentum transfer as low as a few GeV.

In this paper, we present a detailed twist-3 calculations for the two-photon processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-, K^+K^-\) in the perturbative QCD approach based on the \(k_{T}\) factorization theorem. At the twist-2 level, our results are consistent with the predictions given in Refs. [27, 28]. While, with the twist-3 corrections, it is found that both the \(\pi ^{+}\pi ^{-}\) and the \(K^{+}K^{-}\) cross sections agree well with the experiment data [13,14,15]. This paper is organized as follows: In Sect. 2, the related conventions to these processes are introduced at first, next the twist-2 and twist-3 light-cone wave functions are described briefly, then we perform the calculation of the hard kernels with twist-3 corrections. The numerical analysis and discussion are given in Sect. 3. The last section is our summary and conclusion. The expression of the Sudakov function can be found in “Appendix”.

2 Formalism

2.1 Kinematics and conventions

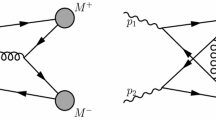
We consider the simplest hadronic processes, \(\gamma _1(p_1,\varepsilon _1^{\lambda _1})\gamma _2(p_2,\varepsilon _2^{\lambda _2})\rightarrow M^+(p_3)M^-(p_4)(M=\pi ,K)\), where the incoming photons are real with momenta \(p_1\), \(p_2\) and polarization vectors \(\varepsilon _1^{\lambda _1}\), \(\varepsilon _2^{\lambda _2}\) with the photon helicities \(\lambda _1,\lambda _2=\pm 1\), M denotes the out-going pseudoscalar mesons with momenta \(p_3\), \(p_4\). The contributions to the \(\gamma \gamma \rightarrow (q{\bar{q}})+(q{\bar{q}})\) amplitude arise from 20 tree-level Feynman diagrams, which can be grouped together into four basic types (a, b, c and d) based on the virtualities of the internal gluon. We depict the four basic Feynman diagrams in Fig. 1. The remaining diagrams arise from permutations of the gluon and quark lines.

Fig. 1
figure 1

Four basic Feynman diagrams for \(\gamma \gamma \rightarrow M^{+}M^{-}(M=\pi ,K)\). The total number of tree-level diagrams in groups \({\mathbf {a}}\), \({\mathbf {b}}\), \({\mathbf {c}}\) and \({\mathbf {d}}\) are 6, 6, 4, and 4, respectively. The grouping is based on the virtualities of the internal gluon

Full size image

For convenience, the amplitude is calculated in the center-of-momentum frame with the momenta of the final mesons along z-axis. \(\theta \) is the scattering angle and Q denotes the two-photon center-of-mass energy. In the light-cone coordinate, a momentum \(A^\mu \) has the form \(A^\mu =(A^+,A^-,{\mathbf {A}}_\perp )\) with \(A^\pm =A^0\pm A^3\) and \({\mathbf {A}}_\perp =(A^1,A^2)\), the scalar product is defined as \(A\cdot B=\frac{1}{2}(A^+B^-+A^-B^+)-{\mathbf {A}}_\perp {\mathbf {B}}_\perp \). Under these conventions, the momenta of photons and mesons read

$$\begin{aligned} p_1&=(2\omega c^2,2\omega s^2,{\mathbf {p}}),\quad p_2=(2\omega s^2,2\omega c^2,-{\mathbf {p}}),\nonumber \\ p_3&=(2\omega ,0,{\mathbf {0}}_\perp ),\quad p_4=(0,2\omega ,{\mathbf {0}}_\perp ), \end{aligned}$$
(2)

and the corresponding polarization vectors of the initial photons can be written as

$$\begin{aligned} \varepsilon _1^+&=\frac{1}{\sqrt{2}}(2sc,-2sc,s^2-c^2,-i),\quad \nonumber \\ \varepsilon _1^-&=\frac{1}{\sqrt{2}}(-2sc,2sc,c^2-s^2,-i),\nonumber \\ \varepsilon _2^+&=\frac{1}{\sqrt{2}}(-2sc,2sc,c^2-s^2,-i),\quad \nonumber \\ \varepsilon _2^-&=\frac{1}{\sqrt{2}}(2sc,-2sc,s^2-c^2,-i) \end{aligned}$$
(3)

with \(\omega =\frac{Q}{2}\), \(s=\sin \frac{\theta }{2}\), \(c=\cos \frac{\theta }{2}\) and \({\mathbf {p}}=(2\omega sc,0)\) for abbreviation. The momenta of the quark and antiquark \(k_1\), \(k_2\) in the \(M^+\) meson and \(k_3\), \(k_4\) in the \(M^-\) meson as labeled in Fig. 1 can be written as

$$\begin{aligned}&k_1=(2x\omega ,0,{\mathbf {k}}_{\perp 1}),\quad k_2=(2{\bar{x}}\omega ,0,-{\mathbf {k}}_{\perp 1}),\nonumber \\&k_3=(0,2y\omega ,{\mathbf {k}}_{\perp 2}),\quad k_4=(0,2{\bar{y}}\omega ,-{\mathbf {k}}_{\perp 2}) \end{aligned}$$
(4)

with \({\bar{x}}\equiv 1-x\) (\({\bar{y}}\equiv 1-y\)). Here x (y) and \({\bar{x}}\) (\({\bar{y}}\)) are the longitudinal momentum fractions of quark and antiquark, respectively, and the transverse momenta \({\mathbf {k}}_{\perp 1}\), \({\mathbf {k}}_{\perp 2}\) are relate to the momenta of the two out-going mesons.

2.2 Light-cone wave functions

The Fierz identity is generally employed to factorize the fermion flow:

$$\begin{aligned} {\overline{q}}_{1\alpha }q_{2\beta }&=\frac{1}{4}I_{\beta \alpha }({\overline{q}}_1q_2) -\frac{1}{4}(i\gamma _5)_{\beta \alpha }({\overline{q}}_1i\gamma ^5q_2)\nonumber \\&\quad +\frac{1}{4}(\gamma _\mu )_{\beta \alpha }({\overline{q}}_1\gamma ^\mu q_2)\nonumber \\&\quad -\frac{1}{4}(\gamma _\mu \gamma _5)_{\beta \alpha }({\overline{q}}_1\gamma ^\mu \gamma ^5q_2)\nonumber \\&\quad +\frac{1}{8}(\sigma _{\mu \nu }\gamma _5)_{\beta \alpha }({\overline{q}}_1\sigma ^{\mu \nu }\gamma ^5q_2). \end{aligned}$$
(5)

Here q and \({\bar{q}}\) are the quark and antiquark field. The Dirac structure \(\gamma ^\mu \gamma ^5\) in Eq. (5) contributes at the twist-2 level, while \(i\gamma ^5\) and \(\sigma ^{\mu \nu }\gamma ^5\) contribute at the twist-3 level.

With the light-cone expansion to twist-3 accuracy, the two-parton light-cone wave functions of \(\pi ^{-}\) can be expressed via the matrix element of the bilocal operator [31,32,33,34]

(6)

where \(f_\pi \) refers to the decay constant of pion and the mass parameter \(\mu _\pi \) is defined as

$$\begin{aligned} \mu _\pi =\frac{m_\pi ^2}{m_u+m_d}, \end{aligned}$$
(7)

where \(m_u\), \(m_d\) are the current quark masses and \(m_\pi \) denotes the pion meson mass. \(\Psi _\pi ^\pi \) is the twist-2 wave function and \(\Psi _{\pi }^{p}\), \(\Psi _{\pi }^{\sigma }\) are two-parton twist-3 wave functions. Due to the SU(2) isotopic symmetry, the wave functions of \(\pi ^{+}\) are identical with the wave functions of \(\pi ^{-}\). Generally, the twist-3 contributions are power-suppressed. However, compared with the twist-2 contributions, the suppression factor \(\mu _\pi /Q\) in the two-parton twist-3 contributions is usually not small enough because of the chiral enhancement effects, i.e., through the relations between light quark masses in the chiral perturbation theory, \(\mu _{\pi }(2~\mathrm {GeV})= 2.43~\mathrm {GeV}\) [35]. Especially, in the intermediate energy region, such as the BELLE experimental range \(2.4\ \mathrm {GeV}<Q<4.1\ \mathrm {GeV}\) [15], one can obtain the suppression factor \(\mu _\pi /Q\sim {\mathcal {O}}(1)\). That is the reason why, in some processes [18, 19, 36,37,38,39,40], the two-parton twist-3 contributions could become even more important than the twist-2 contributions in a few \(\mathrm {GeV}\) region.

Transforming the matrix element of the bilocal operator in Eq. (6) from the coordinate space into the momentum space, one can obtain the light-cone projection operator [34, 41, 42]

(8)

with \(\Psi _{\pi }^{\sigma \prime }=\partial \Psi _{\pi }^\sigma (x,{\mathbf {k}}_\perp )/\partial x\) and \({\bar{p}}^{\mu }=(p^{0},-{\mathbf {p}})\). From the first principles in QCD, the exact transverse momentum dependence of the above wave functions is still unknown. For the convenience of calculations, we assume that \(\Psi _{\pi }^{\pi }\), \(\Psi _{\pi }^{p}\) and \(\Psi _{\pi }^{\sigma }\) have the same transverse momentum dependence. Following the ansatz made in Refs. [22, 43], the wave functions of the pion can be separated into two parts

$$\begin{aligned} \Psi _{\pi }^i(x,{\mathbf {k}}_\perp ,\mu )=\phi _{\pi }^i(x,\mu )\Sigma _{\pi }(x,{\mathbf {k}}_\perp ),\quad (i=\pi ,p,\sigma ). \end{aligned}$$
(9)

One part is the distribution amplitudes \(\phi _{\pi }^{\pi }\), \(\phi _{\pi }^{p}\) and \(\phi _{\pi }^{\sigma }\). Using the conformal symmetry, the distribution amplitudes can be expanded in the Gegenbauer polynomials [33]

$$\begin{aligned} \phi _{\pi }^{\pi }(x,\mu )&=6x\left( 1-x\right) \left[ 1+a_2^\pi (\mu ^2)C_2^{3/2}(2x-1)\nonumber \right. \\&\quad \left. +a_4^\pi (\mu ^2)C_4^{3/2}(2x-1)\right] ,\nonumber \\ \phi _{\pi }^{p}(x,\mu )&=1+\left( 30\eta _{3\pi }(\mu ^{2})-\frac{5}{2}\rho ^{2}_{\pi }(\mu ^{2})\right) C_{2}^{1/2}(2x-1)\nonumber \\&\quad +\left( -3\eta _{3\pi }(\mu ^{2})\omega _{3\pi }(\mu ^{2})-\frac{27}{20}\rho ^{2}_{\pi }(\mu ^{2})\nonumber \right. \\&\quad \left. -\frac{81}{10}\rho ^{2}_{\pi }(\mu ^{2}) a_{2}^{\pi }(\mu ^{2})\right) C_4^{1/2}(2x-1),\nonumber \\ \phi _{\pi }^{\sigma }(x,\mu )&=6x\left( 1-x\right) \left[ 1+\left( 5\eta _{3\pi }(\mu ^{2})-\frac{1}{2}\eta _{3\pi }(\mu ^{2})\omega _{3\pi }(\mu ^{2})\nonumber \right. \right. \\&\quad \left. \left. -\frac{7}{20}\rho ^{2}_{\pi }(\mu ^{2})-\frac{3}{5}\rho ^{2}_{\pi }(\mu ^{2}) a_{2}^{\pi }(\mu ^{2})\right) C_2^{3/2}(2x-1)\right] \end{aligned}$$
(10)

with the normalization conditions

$$\begin{aligned} \int _0^1\mathrm {d}x\phi _{\pi }^{\pi }(x,\mu )=1,&\quad \int _0^1\mathrm {d}x\phi _{\pi }^{p}(x,\mu )=1,\nonumber \\&\quad \int _0^1\mathrm {d}x\phi _{\pi }^{\sigma }(x,\mu )=1. \end{aligned}$$
(11)

Here \(a_{2,4}^\pi \) are the Gegenbauer moments, the twist-3 parameters \(\eta _{3\pi }\), \(\rho _{\pi }^{2}\) are defined as

$$\begin{aligned} \eta _{3\pi }=\frac{f_{3\pi }}{f_{\pi }\mu _{\pi }},\quad \quad \rho _{\pi }^{2}=\frac{\left( m_{u}+m_{d}\right) ^{2}}{m_{\pi }^{2}} \end{aligned}$$
(12)

and the parameters \(f_{3\pi }\), \(\omega _{3\pi }\) are defined in terms of matrix elements of the local three-parton twist-3 operators [33]

$$\begin{aligned}&\langle 0|{\bar{u}}\sigma _{\mu \alpha }\gamma _{5}g_{s}G_{\nu \alpha }d|\pi ^{-}(p)\rangle \nonumber \\&\quad =2if_{3\pi } p_{\mu }p_{\nu },\nonumber \\&\langle 0|{\bar{u}}\sigma _{\mu \alpha }\gamma _{5}\left[ iD_{\beta },g_{s}G_{\nu \alpha }\right] d-(3/7)i\partial _{\beta }{\bar{u}}\sigma _{\mu \alpha }\gamma _{5}g_{s} G_{\nu \alpha }d|\pi ^{-}(p)\rangle \nonumber \\&\quad =\frac{3}{14}if_{3\pi }\omega _{3\pi } p_{\mu }p_{\nu }p_{\beta }. \end{aligned}$$
(13)

The other part is the \(k_\perp \)-dependence function \(\Sigma _{\pi }(x,k_\perp )\). With the constraint from the \(\pi ^{-}\rightarrow \mu ^{-}{\bar{\nu }}_{\mu }\) decay [20], one can obtain

$$\begin{aligned} \int \frac{\mathrm {d}x\mathrm {d}^2{\mathbf {k}}_\perp }{16\pi ^3}\Psi _{\pi }(x,{\mathbf {k}}_\perp ,\mu )=1, \end{aligned}$$
(14)

i.e., the function \(\Sigma _{\pi }(x,{\mathbf {k}}_\perp )\) satisfy the normalization condition

$$\begin{aligned} \int \frac{\mathrm {d}^2{\mathbf {k}}_\perp }{16\pi ^3}\Sigma _{\pi }(x,{\mathbf {k}}_\perp )=1. \end{aligned}$$
(15)

An appropriate candidate for the function \(\Sigma _{\pi }(x,{\mathbf {k}}_\perp )\) is usually assumed to be a simple Gaussian form [22, 44]

$$\begin{aligned} \Sigma _{\pi }(x,{\mathbf {k}}_\perp )=\frac{16\pi ^2\beta _{\pi }^2}{x(1-x)}\mathrm {exp}\left[ -\frac{\beta _{\pi }^2 {\mathbf {k}}_\perp ^2}{x(1-x)}\right] , \end{aligned}$$
(16)

where the oscillator parameter \(\beta _{\pi }\) is determined by the mean square transverse momentum

$$\begin{aligned} \langle {\mathbf {k}}_\perp ^2\rangle _{\pi }=\frac{\displaystyle \int _0^1\mathrm {d}x\displaystyle \int \mathrm {d}^2{\mathbf {k}}_\perp {\mathbf {k}}_\perp ^2|\Psi _{\pi }(x,{\mathbf {k}}_\perp )|^2}{\displaystyle \int _0^1\mathrm {d}x\displaystyle \int \mathrm {d}^2{\mathbf {k}}_\perp |\Psi _{\pi }(x,{\mathbf {k}}_\perp )|^2} =\frac{1}{2\beta _{\pi }^2}\frac{\displaystyle \int _0^1\mathrm {d}x|\phi _{\pi }(x)|^2}{\displaystyle \int _0^1\mathrm {d}x\frac{|\phi _{\pi }(x)|^2}{x(1-x)}}. \end{aligned}$$
(17)

The detailed discussions about the choice of the oscillator parameter \(\beta _{\pi }\) are shown in Refs. [22, 44]. In this work, we will take the value \(\langle {\mathbf {k}}_\perp ^2\rangle _{\pi }^{1/2}=0.35~\mathrm {GeV}\), which is compatible with the \(\pi ^{0}\rightarrow \gamma \gamma \) constraint [20].

For the \(K^{-}\) case, the matrix element of the bilocal operator can be expressed as [45]

(18)

where \(f_{K}\) refers to the decay constant of kaon, and the chiral enhancement parameter is defined as \(\mu _{K}=m_{K}^2/(m_u+m_s)\), \(m_u\) and \(m_s\) are the current quark masses and \(m_K\) denotes the kaon meson mass. We should note that the wave functions of \(K^{+}\) are given by \(\Psi _{K^{+}}^{i}(x,{\mathbf {k}}_\perp ) =\Psi _{K}^{i}(1-x,{\mathbf {k}}_\perp )\) [45].

Similar to the pion case, the wave functions of the kaon meson can also be written as

$$\begin{aligned} \Psi _{K}^{i}(x,{\mathbf {k}}_\perp ,\mu )=\phi _{K}^{i}(x,\mu )\Sigma _{K}(x,{\mathbf {k}}_\perp ),\quad (i=K,p,\sigma ) \end{aligned}$$
(19)

with

$$\begin{aligned} \Sigma _{K}(x,{\mathbf {k}}_\perp )=\frac{16\pi ^2\beta _{K}^2}{x(1-x)}\mathrm {exp}\left[ -\frac{\beta _{K}^2 {\mathbf {k}}_\perp ^2}{x(1-x)}\right] . \end{aligned}$$
(20)

Here we have adopted the approximation \(\langle {\mathbf {k}}_\perp ^2\rangle _{K}\approx \langle {\mathbf {k}}_\perp ^2\rangle _{\pi }\). The corresponding distribution amplitudes \(\phi _{K}^{K}\), \(\phi _{K}^{p}\) and \(\phi _{K}^{\sigma }\) have the forms [45]

$$\begin{aligned} \phi _{K}^{K}(x,\mu )&= 6x\left( 1-x\right) \left[ 1+a_1^KC_1^{3/2}(2x-1)+a_2^KC_2^{3/2}(2x-1)\right] ,\nonumber \\ \phi _{K}^{p}(x,\mu )&= 1+3\rho _{+}^{K}\left( 1+6a_{2}^{K}\right) -9\rho _{-}^{K}a_{1}^{K}\nonumber \\&\quad +\left[ \frac{27}{2}\rho _{+}^{K}a_{1}^{K}-\rho _{-}^{K}\left( \frac{3}{2}+27a_{2}^{K} \right) \right] C_{1}^{1/2}(2x-1)\nonumber \\&\quad +\left( 30\eta _{3K}+15\rho ^{K}_{+}a_{2}^{K}-3\rho _{-}^{K}a_{1}^{K}\right) C_{2}^{1/2}(2x-1)\nonumber \\&\quad +\left( 10\eta _{3K}\lambda _{3K}-\frac{9}{2}\rho ^{K}_{-}a_{2}^{K}\right) C_{3}^{1/2}(2x-1)\nonumber \\&\quad -3\eta _{3K}\omega _{3K}C_{4}^{1/2}(2x-1)\nonumber \\&\quad +\frac{3}{2}\left( \rho ^{K}_{+} +\rho ^{K}_{-}\right) \left( 1-3a_{1}^{K}+6a_{2}^{K}\right) \ln x\nonumber \\&\quad +\frac{3}{2}\left( \rho ^{K}_{+}-\rho ^{K}_{-}\right) \left( 1+3a_{1}^{K} +6a_{2}^{K}\right) \ln (1-x),\nonumber \\ \phi _{K}^{\sigma }(x,\mu )&= 6x\left( 1-x\right) \bigg [1+\frac{3}{2}\rho ^{K}_{+}+15\rho ^{K}_{+}a_{2}^{K}\nonumber \\&\quad -\frac{15}{2}\rho ^{K}_{-}a_{1}^{K} +\left( 3\rho _{+}^{K}a_{1}^{K}-\frac{15}{2}\rho _{-}^{K}a_{2}^{K} \right) C_{1}^{3/2}(2x-1)\nonumber \\&\quad +\left( 5\eta _{3K}-\frac{1}{2}\eta _{3K}\omega _{3K} +\frac{3}{2}\rho _{+}^{K}a_{2}^{K}\right) C_{2}^{3/2}(2x-1)\nonumber \\&\quad +\eta _{3K}\lambda _{3K}C_{3}^{3/2}(2x-1)\nonumber \\&\quad +\frac{3}{2}\left( \rho ^{K}_{+} +\rho ^{K}_{-}\right) \left( 1-3a_{1}^{K}+6a_{2}^{K}\right) \ln x\nonumber \\&\quad +\frac{3}{2}\left( \rho ^{K}_{+}-\rho ^{K}_{-}\right) \left( 1+3a_{1}^{K} +6a_{2}^{K}\right) \ln (1-x) \bigg ] \end{aligned}$$
(21)

with the normalization conditions

$$\begin{aligned} \int _0^1\mathrm {d}x\phi _{K}^{K}(x,\mu )&=1,\quad \int _0^1\mathrm {d}x\phi _{K}^{p}(x,\mu )=1,\quad \nonumber \\ \int _0^1\mathrm {d}x\phi _{K}^{\sigma }(x,\mu )&=1-\rho _{+}^{K}. \end{aligned}$$
(22)

Here the SU(3) symmetry breaking effects have already been taken into account. The parameters \(a_{1,2}^{K}\) are the first two nonvanishing Gegenbauer moments, and the twist-3 parameters \(\eta _{3K}\), \(\rho _{\pm }^{K}\) read

$$\begin{aligned} \eta _{3K}=\frac{f_{3K}}{f_{K}\mu _{K}},\quad \rho _{+}^{K}=\frac{\left( m_{s}+m_{u}\right) ^{2}}{m_{K}^{2}}, \quad \rho _{-}^{K}=\frac{m_{s}^{2}-m_{u}^{2}}{m_{K}^{2}}, \end{aligned}$$
(23)

where the parameters \(f_{3K}\), \(\omega _{3K}\), \(\lambda _{3K}\) are defined in terms of matrix elements of the local three-parton twist-3 operators [33]

$$\begin{aligned}&\langle 0|{\bar{u}}\sigma _{\mu \alpha }\gamma _{5}g_{s}G_{\nu \alpha }s|K^{-}(p)\rangle \nonumber \\&\quad =2i f_{3K} p_{\mu }p_{\nu },\nonumber \\&\langle 0|{\bar{u}}\sigma _{\mu \alpha }\gamma _{5}\left[ iD_{\beta },g_{s} G_{\nu \alpha }\right] s-(3/7)i\partial _{\beta } {\bar{u}} \sigma _{\mu \alpha }\gamma _{5} g_{s} G_{\nu \alpha }s|K^{-}(p)\rangle \nonumber \\&\quad =\frac{3i}{14} f_{3K}\omega _{3K} p_{\mu }p_{\nu }p_{\beta },\nonumber \\&\langle 0|{\bar{u}}i\overleftarrow{D}_{\beta }\sigma _{\mu \alpha }\gamma _{5}g_{s}G_{\nu \alpha }s-{\bar{u}}\sigma _{\mu \alpha }\gamma _{5}g_{s} G_{\nu \alpha }i\overrightarrow{D}_{\beta } s|K^{-}(p)\rangle \nonumber \\&\quad =\frac{i}{7}f_{3K}\lambda _{3K} p_{\mu }p_{\nu }p_{\beta }. \end{aligned}$$
(24)

Using the leading-order renormalization group equations, the scale dependence of the various parameters is given by

$$\begin{aligned} a_{n}^{\pi }(\mu ^{2})&=L^{\gamma ^{(0)}_{n}/\beta _{0}}a_{n}^{\pi }\left( \mu ^{2}_{0}\right) ,&\mu _{\pi }(\mu ^{2})&=L^{\gamma ^{(0)}_{\mu _{\pi }}/\beta _{0}}\mu _{\pi }\left( \mu ^{2}_{0}\right) , \nonumber \\ \rho _{\pi }^{2}(\mu ^{2})&=L^{\gamma ^{(0)}_{\rho _{\pi }^{2}}/\beta _{0}}\rho _{\pi }^{2}\left( \mu ^{2}_{0}\right) ,\nonumber \\ f_{3\pi }(\mu ^{2})&=L^{\gamma ^{(0)}_{f_{3\pi }}/\beta _{0}}f_{3\pi }\left( \mu ^{2}_{0}\right) ,&\eta _{3\pi }(\mu ^{2})&=L^{\gamma ^{(0)}_{\eta _{3\pi }}/\beta _{0}}\eta _{3\pi }\left( \mu ^{2}_{0}\right) ,\nonumber \\ \omega _{3\pi }(\mu ^{2})&=L^{\gamma ^{(0)}_{\omega _{3\pi }}/\beta _{0}}\omega _{3\pi }\left( \mu ^{2}_{0}\right) , \end{aligned}$$
(25)

for the pion and

$$\begin{aligned} a_{n}^{K}(\mu ^{2})&=L^{\gamma ^{(0)}_{n}/\beta _{0}}a_{n}^{K}(\mu ^{2}_{0}),\quad \mu _{K}(\mu ^{2})=L^{\gamma ^{(0)}_{\mu _{K}}/\beta _{0}}\mu _{K}(\mu ^{2}_{0}),\nonumber \\ \rho _{+}^{K}(\mu ^{2})&=L^{\gamma ^{(0)}_{\rho _{+}^{K}}/\beta _{0}}\rho _{+}^{K}(\mu ^{2}_{0}),\quad \rho _{-}^{K}(\mu ^{2})=L^{\gamma ^{(0)}_{\rho _{-}^{K}}/\beta _{0}}\rho _{-}^{K}(\mu ^{2}_{0}),\nonumber \\ f_{3K}(\mu ^{2})&=L^{55/(36\beta _{0})}f_{3K}(\mu ^{2}_{0})\nonumber \\&\quad +\frac{2}{19}\left( L^{1/\beta _{0}} -L^{55/(36\beta _{0})}\right) [f_{K}m_{s}](\mu ^{2}_{0})\nonumber \\&\quad +\frac{6}{65}\left( L^{55/(36\beta _{0})} -L^{17/(9\beta _{0})}\right) \left[ f_{K}m_{s}a_{1}^{K}\right] (\mu ^{2}_{0}),\nonumber \\ {[f_{3K}\omega _{3K}]}(\mu ^{2})&=L^{26/(9\beta _{0})}[f_{3K}\omega _{3K}](\mu ^{2}_{0})\nonumber \\&\quad +\frac{1}{170}\left( L^{1/\beta _{0}} -L^{26/(9\beta _{0})}\right) [f_{K}m_{s}](\mu ^{2}_{0})\nonumber \\&\quad +\frac{1}{10}\left( L^{17/(9\beta _{0})} -L^{26/(9\beta _{0})}\right) \left[ f_{K}m_{s}a_{1}^{K}\right] (\mu ^{2}_{0})\nonumber \\&\quad +\frac{2}{15}\left( L^{43/(18\beta _{0})} -L^{26/(9\beta _{0})}\right) \left[ f_{K}m_{s}a_{2}^{K}\right] (\mu ^{2}_{0}), \nonumber \\ {[f_{3K}\lambda _{3K}]}(\mu ^{2})&=L^{37/(18\beta _{0})}[f_{3K}\lambda _{3K}](\mu ^{2}_{0})\nonumber \\&\quad -\frac{14}{67}\left( L^{1/\beta _{0}} -L^{37/(18\beta _{0})}\right) [f_{K}m_{s}](\mu ^{2}_{0})\nonumber \\&\quad +\frac{14}{5}\left( L^{17/(9\beta _{0})} -L^{37/(18\beta _{0})}\right) \left[ f_{K}m_{s}a_{1}^{K}\right] (\mu ^{2}_{0})\nonumber \\&\quad -\frac{4}{11}\left( L^{43/(18\beta _{0})} -L^{37/(18\beta _{0})}\right) \left[ f_{K}m_{s}a_{2}^{K}\right] (\mu ^{2}_{0}), \end{aligned}$$
(26)

for the kaon with the evolution factor \(L=\alpha _s(\mu ^2)/\alpha _s(\mu _0^2)\) and \(\beta _{0}=(33-2 n_{f})/12\). To the leading logarithmic accuracy, the QCD running coupling constant can be expressed as

$$\begin{aligned} \alpha _s(\mu ^2)=\frac{\pi }{\beta _{0}\ln \left( \frac{\mu ^2}{\Lambda _{QCD}^2}\right) }, \end{aligned}$$
(27)

and the anomalous dimensions are given by

$$\begin{aligned} \gamma ^{(0)}_{n}&=C_F\left( \psi (n+2)+\gamma _E-\frac{3}{4}-\frac{1}{2(n+1)(n+2)}\right) ,\nonumber \\ \gamma ^{(0)}_{\mu _{\pi }}&=\gamma ^{(0)}_{\mu _{K}}=-1,\quad \gamma ^{(0)}_{\rho _{\pi }^{2}}=\rho _{\pm }^{K}=2,\nonumber \\ \gamma ^{(0)}_{f_{3\pi }}&=\frac{7}{12}C_{F}+ \frac{1}{4}C_{A},\quad \gamma ^{(0)}_{\eta _{3\pi }}=\frac{4}{3}C_{F}+\frac{1}{4}C_{A},\quad \nonumber \\ \gamma ^{(0)}_{\omega _{3\pi }}&=-\frac{7}{24}C_{F}+\frac{7}{12}C_{A}, \end{aligned}$$
(28)

with \(C_{F}=4/3\) and \(C_{A}=3\).

In perturbative QCD approach, the convolution of wave functions and hard kernels needs to be performed in the transverse configuration b-space. With the definition

$$\begin{aligned} {\hat{\Psi }}(x,{\mathbf {b}},\mu )=\int \frac{\mathrm {d}^{2}{\mathbf {k}}_\perp }{(2\pi )^{2}}\Psi (x,{\mathbf {k}}_\perp ,\mu )e^{-i{\mathbf {k}}_\perp \cdot {\mathbf {b}}}, \end{aligned}$$
(29)

one can obtain that the full soft wave functions of the pion and kaon in the transverse configuration b-space have the forms

$$\begin{aligned}&{\hat{\Psi }}_{M}^{i}(x,{\mathbf {b}},\mu )\nonumber \\&\quad =\phi _{M}^{i}(x,\mu ){\hat{\Sigma }}_{M}(x,{\mathbf {b}}),\quad (M=\pi ,K;\ i=\pi /K, p, \sigma ) \end{aligned}$$
(30)

where the Fourier transformed functions \({\hat{\Sigma }}_{M}(x,b)\) read

$$\begin{aligned} {\hat{\Sigma }}_{M}(x,{\mathbf {b}})&=\int \frac{\mathrm {d}^{2}{\mathbf {k}}_\perp }{(2\pi )^{2}}\Sigma _{M}(x,{\mathbf {k}}_\perp )e^{-i{\mathbf {k}}_\perp \cdot {\mathbf {b}}}\nonumber \\&=4\pi \ \mathrm {exp}\left[ -\frac{x(1-x){\mathbf {b}}^2}{4\beta _{M}^2}\right] . \end{aligned}$$
(31)

2.3 The helicity amplitudes with twist-3 contributions

In the perturbative QCD approach, the helicity amplitudes can be expressed as the convolution between the soft hadron wave functions and the hard kernels with respect to both the longitudinal momentum fractions and the transverse separation of quark and antiquark. To the \(\pi ^+\pi ^-\) production in two-photon collision, the helicity amplitudes have the form [26, 29]

$$\begin{aligned} {\mathcal {M}}_{\lambda _1\lambda _2}{(Q,\theta )}&= \int _0^1\mathrm {d}x\mathrm {d}y\int \frac{\mathrm {d}^2{\mathbf {b}}_1}{4\pi }\frac{\mathrm {d}^2{\mathbf {b}}_{2}}{4\pi }\nonumber \\&\quad \times \sum _{i,j=\pi ,p,\sigma ,\sigma ^{\prime }}{\hat{\Psi }}_\pi ^i(x,{\mathbf {b}}_1,\mu _F)\nonumber \\&\quad \times {\hat{T}}_{ij}^{\lambda _1\lambda _2}(x,y,Q,\theta ,{\mathbf {b}}_{1},{\mathbf {b}}_{2},\mu _R)\nonumber \\&\quad \times {\hat{\Psi }}_\pi ^j(y,{\mathbf {b}}_2,\mu _F)S_t(x)S_t(y)\nonumber \\&\quad \times \exp [-S(x,y,{\mathbf {b}}_1,{\mathbf {b}}_2,\mu _F,\mu _R)] \end{aligned}$$
(32)

with

$$\begin{aligned} {\hat{\Psi }}_\pi ^{\sigma ^{\prime }}(x,{\mathbf {b}}_1,\mu _F)&=\frac{\partial {\hat{\Psi }}_\pi ^\sigma (x,{\mathbf {b}}_1,\mu _F)}{\partial x},\quad \nonumber \\ {\hat{\Psi }}_\pi ^{\sigma ^{\prime }}(y,{\mathbf {b}}_2,\mu _F)&=\frac{\partial {\hat{\Psi }}_\pi ^\sigma (y,{\mathbf {b}}_2,\mu _F)}{\partial y}. \end{aligned}$$
(33)

\({\hat{T}}_{ij}^{\lambda _1\lambda _2}\) represent the Fourier transformed hard kernels

$$\begin{aligned}&{\hat{T}}_{ij}^{\lambda _1\lambda _2}(x,y,Q,\theta ,{\mathbf {b}}_{1},{\mathbf {b}}_{2},\mu _R)\nonumber \\&\quad = \int \frac{\mathrm {d}^2{\mathbf {k}}_{\perp 1}}{(2\pi )^2}\frac{\mathrm {d}^2{\mathbf {k}}_{\perp 2}}{(2\pi )^2} T_{ij}^{\lambda _1\lambda _2}(x,y,Q,\theta ,{\mathbf {k}}_{\perp 1},{\mathbf {k}}_{\perp 2},\mu _R)\nonumber \\&\qquad \times \mathrm {exp}[-i {\mathbf {k}}_{\perp 1}\cdot {\mathbf {b}}_1-i {\mathbf {k}}_{\bot 2}\cdot {\mathbf {b}}_2], \end{aligned}$$
(34)

where \(T_{ij}^{\lambda _1\lambda _2}\) with the transverse momentum \({\mathbf {k}}_{\perp 1}\), \({\mathbf {k}}_{\perp 2}\) kept can be calculated perturbatively by Feynman rules. In the helicity amplitudes, the scripts \(i,j=\pi \) correspond to the twist-2\(\times \)twist-2 term, and the scripts \(i,j=p,\sigma ,\sigma ^{\prime }\) correspond to the two-parton (\({\bar{q}}q\)) twist-3\(\times \)twist-3 terms. It is noteworthy that the two-parton twist-2\(\times \)twist-3 terms vanish because of the spin structure of the corresponding hard kernels. Compared with the twist-2\(\times \)twist-2 contributions, the contributions from the two-parton twist-3\(\times \)twist-3 ones are generally regarded as power-suppressed. However in a few GeV region, the suppression factor is \(\mu _{\pi }^{2}/Q^{2}\sim {\mathcal {O}}(1)\) as a consequence of the chiral enhancement effects. So the two-parton twist-3\(\times \)twist-3 contributions become important in this energy region. While, compared with the twist-2\(\times \)twist-2 contributions, the contributions from the three-parton (\({\bar{q}}qg\)) twist-3\(\times \)twist-3 terms and that from the two-parton twist-2\(\times \)twist-4 terms are strongly suppressed by the factors \(f_{3\pi }/(f_{\pi }Q)\) and \(m_{\pi }^{2}/Q^{2}\) respectively. According to the factors \(f_{3\pi }/(f_{\pi }Q)\) and \(m_{\pi }^{2}/Q^{2}\) being at the order of \(10^{-2}\) in the intermediate energy region, these two contributions would be much smaller than the twist-2\(\times \)twist-2 and two-parton twist-3\(\times \)twist-3 contributions in this energy region. A similar analysis have also been given in the studies of the time-like electromagnetic form factors [38, 46]. Recently, the explicit calculations of the three-parton twist-3\(\times \)twist-3 [40, 47] and two-parton twist-2\(\times \)twist-4 contributions [40] for the pion electromagnetic form factors have been performed, and the numerical results have shown that these two contributions are at least an order of magnitude smaller than the twist-2\(\times \)twist-2 and the two-parton twist-3\(\times \)twist-3 contributions, which is consistent with the previous analysis [46]. So in this work, we will neglect the contributions from the three-parton twist-3\(\times \)twist-3 terms and the two-parton twist-2\(\times \)twist-4 terms.

With the transverse momentum \({\mathbf {k}}_{\perp }\) retained, an important property of the hard kernels needed to make clear is the gauge invariance. Here we present a brief analysis. As pointed out in the Refs. [48, 49], one may encounter the problem of gauge dependence caused by the off-shellness of partons in a \({\mathbf {k}}_{\perp }\)-dependent hard kernel. For exclusive processes, it have been proven that the hard kernels derived in the \(k_{T}\) factorization are gauge invariance to all orders in \(\alpha _{s}\) at twist-2 level [50, 51]. While at high twist level, the situation becomes more complex. As the results shown in the \(\pi ^{0}\) [42] and \(\rho ^{0}\) [52] photoproduction processes, the two-parton twist-3 contributions must be combined with the three-parton twist-3 contributions in order to guarantee gauge invariance. In fact, the gauge dependence of the two-parton twist-3 hard kernel is due to the terms proportional to the transverse momentum in the hard kernel, and it have been shown in Ref. [47] that the gauge dependence proportional to the transverse momentum in the numerator of the two-parton hard kernel and the gauge dependence associated with the three-parton Fock state exactly cancel each other. In other words, if the terms proportional to the transverse momentum in the numerators of the two-parton hard kernels (power-suppressed by 1 / Q) and the three-parton Fock state (strongly suppressed by the nonperturbative parameter \(f_{3\pi }\)) are precluded simultaneously, the two sources of gauge dependence would disappear, and the \({\mathbf {k}}_{\perp }\)-dependent two-parton hard kernels would become gauge invariance in the same way as the collinear case [53]. In this work, we employ the \(k_{T}\) factorization theorem proposed in Refs. [30, 54], in which only the transverse momentum dependence in the denominators of the two-parton hard kernels is retained. As analyzed above, the \({\mathbf {k}}_{\perp }\)-dependent two-parton hard kernels in our calculations are gauge invariance. In the following calculations of the hard kernels, the covariant gauge is adopted.

Next we will show our procedure to the Fourier transformation of the hard kernels by means of a specific Feynman diagram in the Group \({\mathbf {a}}\) in Fig. 1 as an example. The hard kernels \(T_{a_1ij}^{\lambda _1\lambda _2}\) with the subscript “\(a_1\)” specifically refer to the results of one of the six diagrams in Group \({\mathbf {a}}\). Its leading-twist contributions are illustrated as

$$\begin{aligned}&T_{a_1\pi \pi }^{++}(x,y,Q,\theta ,{\mathbf {k}}_{\perp 1},{\mathbf {k}}_{\perp 2},\mu _R)\nonumber \\&\quad = \frac{256}{9}\frac{i e_u^2\kappa _{1} s^2c^2\omega ^4(xy+{\bar{x}}{\bar{y}})}{\left( {\tilde{q}}_1^2+i \epsilon \right) \left( {\tilde{q}}_2^2+i \epsilon \right) ({\tilde{g}}^2+i \epsilon )},\nonumber \\&T_{a_1\pi \pi }^{+-}(x,y,Q,\theta ,{\mathbf {k}}_{\perp 1},{\mathbf {k}}_{\perp 2},\mu _R)\nonumber \\&\quad = \frac{256}{9}\frac{i e_u^2\kappa _{1} s^2c^2\omega ^4({\bar{x}}y+x{\bar{y}})}{\left( {\tilde{q}}_1^2+i \epsilon \right) \left( {\tilde{q}}_2^2+i \epsilon \right) ({\tilde{g}}^2+i \epsilon )} \end{aligned}$$
(35)

with the factor \(\kappa _{1}=\alpha \alpha _{s}(\mu _R)\pi ^{2}f_{\pi }^{2}\). Here the terms contained the transverse momentum in the numerators, which are power-suppressed, have been dropped. And the denominators of the corresponding quark and gluon propagators are

$$\begin{aligned} {\tilde{q}}_1^2&=4s^2(c^2-{\bar{x}})\omega ^2-({\mathbf {p}}-{\mathbf {k}}_{\perp 1})^2,\nonumber \\ {\tilde{q}}_2^2&=4s^2(c^2-y)\omega ^2-({\mathbf {p}}+{\mathbf {k}}_{\perp 2})^2,\nonumber \\ {\tilde{g}}^2&=4{\bar{x}}y\omega ^2-{\mathbf {K}}_{\perp }^2 \end{aligned}$$
(36)

with

$$\begin{aligned} {\mathbf {K}}_\perp ={\mathbf {k}}_{\perp 1}-{\mathbf {k}}_{\perp 2}. \end{aligned}$$
(37)

The convolution formula in Eq. (32) involves two independent scales of this process, the factorization scale \(\mu _F\) and the renormalization scale \(\mu _R\). In analogy to the cases of the pion electromagnetic form factor [21, 37, 55] and transition form factor [56,57,58], the transverse separation \(b_1\) and \(b_2\) of the pion wave functions provide the factorization scales \(\mu _{Fi}=1/b_i(i=1,2)\), below which the QCD dynamics is regarded as being nonperturbative and can be absorbed into the the soft wave function. While the renormalization scale \(\mu _R=t\) is set to the largest mass scale associated with the momentum of the internal hard gluon propagators in order to minimize the higher-order QCD corrections.

To simplify the calculation, the hierarchy \(Q^{2}\gg {\bar{x}} Q^{2}\sim y Q^{2}\gg {\bar{x}} y Q^{2},~{\mathbf {k}}_{1\perp }^{2},~{\mathbf {k}}_{2\perp }^{2}\) is postulated in the small-\({\bar{x}}\), y region, as elaborated in Refs. [55, 59]. Under this hierarchy, one can ignore the transverse momentum dependence in the quark propagators and just keep it in the gluon propagator to regulate the endpoint singularity, then the hard kernels in Eq. (35) are simplified as

$$\begin{aligned}&T_{a_1\pi \pi }^{++}(x,y,Q,\theta ,{\mathbf {k}}_{\perp 1},{\mathbf {k}}_{\perp 2},\mu _R)\nonumber \\&\quad = \frac{16}{9}\frac{i e_u^2\kappa _{1}c^2(xy+{\bar{x}}{\bar{y}})}{s^2x{\bar{y}}}\frac{1}{({\tilde{g}}^2+i \epsilon )},\nonumber \\&T_{a_1\pi \pi }^{+-}(x,y,Q,\theta ,{\mathbf {k}}_{\perp 1},{\mathbf {k}}_{\perp 2},\mu _R)\nonumber \\&\quad = \frac{16}{9}\frac{i e_u^2\kappa _{1} c^2({\bar{x}}y+x{\bar{y}})}{s^2x{\bar{y}}}\frac{1}{({\tilde{g}}^2+i \epsilon )}. \end{aligned}$$
(38)

By using the Fourier transformation of the propagators regularized with the \(i \epsilon \) prescription

$$\begin{aligned} \int \frac{\mathrm {d}^2{\mathbf {k}}_\perp }{(2\pi )^2} \frac{\mathrm {exp}[-i {\mathbf {k}}_\perp \cdot {\mathbf {b}}]}{s-{\mathbf {k}}_\perp ^2+i \epsilon } =\left\{ \begin{array}{ll} -\frac{i }{4}\mathrm {H}_0^{(1)}(\sqrt{s}b) &{} \quad {\text{ for }\quad s>0}\\ \\ -\frac{1}{2\pi }\mathrm {K}_0(\sqrt{-s}b) &{} \quad {\text{ for }\quad s<0} \end{array} \right. \, , \end{aligned}$$
(39)

one can obtain the Fourier transformed hard kernels (\(b=|{\mathbf {b}}_{1}|\))

$$\begin{aligned}&{\hat{T}}_{a_1\pi \pi }^{++}(x,y,Q,\theta ,{\mathbf {b}}_{1},{\mathbf {b}}_{2},\mu _R)\nonumber \\&\quad = \frac{4}{9}e_u^2\kappa _{1}\frac{c^2(xy+{\bar{x}}{\bar{y}})}{s^2x{\bar{y}}}\mathrm {H}_0^{(1)}(2\omega \sqrt{{\bar{x}}y}b)\delta ^{2}({\mathbf {b}}_{1}-{\mathbf {b}}_{2}),\nonumber \\&{\hat{T}}_{a_1\pi \pi }^{+-}(x,y,Q,\theta ,{\mathbf {b}}_{1},{\mathbf {b}}_{2},\mu _R)\nonumber \\&\quad = \frac{4}{9}e_u^2\kappa _{1}\frac{c^2({\bar{x}}y+x{\bar{y}})}{s^2x{\bar{y}}}\mathrm {H}_0^{(1)}(2\omega \sqrt{{\bar{x}}y}b)\delta ^{2}({\mathbf {b}}_{1}-{\mathbf {b}}_{2}). \end{aligned}$$
(40)

Here \(\mathrm {H}_0^{(1)}\) and \(\mathrm {K}_0\) denote Hankel and modified Bessel function. As a consequence of the above simplification, the hard kernels in Eq. (40) only depend on a single b parameter. The underlying physics picture is that, the virtual quark lines involved in the hard kernels are thought of as being far from mass shell, and shrunk to a point [21, 26].

There are two types of resummation of the higher-order effects: the region with large transverse separation b for Sudakov resummation and the small longitudinal momentum fraction x region for threshold resummation. The Sudakov resummation of the double logarithms \(\alpha _{s}\ln ^{2}[x/(Q^{2}b^{2})]\) produced by overlapping collinear and soft divergencies for massless quarks as well as the renormalization group equation transformation from the factorization scale 1 / b to the renormalization scale t, are incorporated into the Sudakov factor \(\mathrm {exp}[-S]\). In next-to-leading logarithm approximation, the Sudakov exponent S reads [21, 26, 60]

$$\begin{aligned} S(x,y,b,Q,t)&=s(x,b,Q)+s({\bar{x}},b,Q)+s(y,b,Q)\nonumber \\&\quad +s({\bar{y}},b,Q) -\frac{2}{\beta _{0}}\mathrm {ln}\frac{\mathrm {ln}(t/\Lambda _{QCD})}{\mathrm {ln}(1/(b/\Lambda _{QCD}))}, \end{aligned}$$
(41)

where the function s(x, b, Q) is originally derived by Botts and Sterman [23] and later on slightly improved, for instance, by Li [21] and Kroll [60] et al. The explicit expression of s(x, b, Q) is given in “Appendix”. One can find that the Sudakov factor exhibits a strong fall off at large b. And this property makes the nonperturbative contributions from large b, no matter what x is, less important.

Since there exists the end-point enhancement in the two-parton twist-3 contributions (logarithmical enhancement) for the scattering process \(\gamma \gamma \rightarrow \pi ^{+}\pi ^{-}\) [18, 19], the Sudakov factor \(\mathrm {exp}[-S]\) is still not effective enough to suppress the nonperturbative contributions from small x region, which would spoil the perturbative calculation. It had been argued in Ref. [30] that as the end-point region is important, the corresponding large double logarithms \(\alpha _{s}\mathrm {ln}^2x\) that arise from the higher-order corrections also need to be organized to all orders, and into a jet function \(S_{t}(x)\) as a consequence of threshold resummation. In next-to-leading logarithm accuracy, the jet function \(S_{t}(x)\) can be parameterized into a universal form [30, 61]

$$\begin{aligned} S_t(x,Q)=\frac{2^{1+2c}\Gamma (3/2+c)}{\sqrt{\pi }\Gamma (1+c)}\left[ x(1-x)\right] ^{c}. \end{aligned}$$
(42)

In Ref. [57], Li and Mishima have proposed a parabolic parametrization for the parameter c, and frozen c at \(c=1\), when it exceeds unity:

$$\begin{aligned} c=0.04Q^2-0.51Q+1.87. \end{aligned}$$
(43)

Since the factor \(S_{t}(x)\) drops rapidly as \(x\rightarrow 0,1\), the end-point singularities are eliminated and the nonperturbative contributions from the dangerous end-point regions are suppressed effectively.

After including the above two types of resummation, both the twist-2 and twist-3 contributions are well-behaved, and that results in the perturbative calculation more self-consistent. Performing the integration over \({\mathbf {b}}_{2}\), the helicity amplitudes in Eq. (32) can be then rewritten as a much clearer and simpler form in a single-b form

$$\begin{aligned}&{\mathcal {M}}_{\lambda _1\lambda _2}{(Q,\theta )} = \int _0^1\mathrm {d}x\mathrm {d}y\int \frac{\mathrm {d}^2{\mathbf {b}}}{(4\pi )^2}\sum _{i,j=\pi ,p,\sigma ,\sigma ^{\prime }}{\hat{\Psi }}_{\pi }^{i}(x,{\mathbf {b}},1/b)\nonumber \\&\qquad \times {\hat{T}}_{\lambda _1\lambda _2}^{ij}(x,y,Q,\theta ,{\mathbf {b}},t) {\hat{\Psi }}_{\pi }^{j}(y,{\mathbf {b}},1/b)\nonumber \\&\qquad \times S_t(x)S_t(y)\exp [-S(x,y,Q,b,t)]. \end{aligned}$$
(44)

Making the substitution \(\int \mathrm {d}^2{\mathbf {b}}\rightarrow \int b\mathrm {d}b\mathrm {d}\varphi \) and performing the integral over the polar angle \(\varphi \), we can obtain the helicity amplitudes for \(\gamma \gamma \rightarrow \pi ^+\pi ^-\) process in the conjugate b space by summing up all of the 20 Feynman diagrams

$$\begin{aligned}&{\mathcal {M}}_{\lambda _1\lambda _2}{(Q,\theta )} = \int _0^1\mathrm {d}x\mathrm {d}y\int \frac{b\mathrm {d}b}{(4\pi )^2} \sum _{n=a}^{b,c,d}\nonumber \\&\qquad \times \left( \sum _{i,j=\pi }^{p,\sigma ,\sigma ^{\prime }}{\hat{\Psi }}_{\pi }^{i}(x,b,1/b) {\hat{T}}^{\lambda _1\lambda _2}_{nij}(x,y,Q,\theta ,b,t_{n}) {\hat{\Psi }}_{\pi }^{j}\right. \nonumber \\&\qquad \left. \phantom {\left( \sum _{i,j=\pi }^{p,\sigma ,\sigma ^{\prime }}{\hat{\Psi }}_{\pi }^{i}(x,b,1/b) {\hat{T}}^{\lambda _1\lambda _2}_{nij}(x,y,Q,\theta ,b,t_{n}) {\hat{\Psi }}_{\pi }^{j}(y,b,1/b)\right. }\times (y,b,1/b)S_t(x)S_t(y)\exp [-S(x,y,Q,b,t_{n})]\right) \end{aligned}$$
(45)

with the twist-2 hard kernels

$$\begin{aligned} {\hat{T}}_{a\pi \pi }^{++}&= \frac{4}{9}e_u^2\kappa _{1} \frac{xy+{\bar{x}}{\bar{y}}}{s^2c^2x{\bar{y}}} \mathrm {F}(s_a,b), \nonumber \\ {\hat{T}}_{b\pi \pi }^{++}&= \frac{4}{9}e_d^2\kappa _{1} \frac{xy+{\bar{x}}{\bar{y}}}{s^2c^2{\bar{x}}y} \mathrm {F}(s_b,b), \nonumber \\ {\hat{T}}_{c\pi \pi }^{++}&= \frac{4}{9}e_ue_d\kappa _{1} \left( \frac{xy+{\bar{x}}{\bar{y}}}{s^2xy}+ \frac{xy+{\bar{x}}{\bar{y}}}{c^2{\bar{x}}{\bar{y}}}\right) \mathrm {J}_0(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\pi \pi }^{++}&= \frac{4}{9}e_ue_d\kappa _{1} \left( \frac{xy+{\bar{x}}{\bar{y}}}{c^2xy}+\frac{xy+{\bar{x}}{\bar{y}}}{s^2{\bar{x}}{\bar{y}}} \right) \mathrm {J}_0(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(46)
$$\begin{aligned} {\hat{T}}_{a\pi \pi }^{+-}&= \frac{4}{9}e_u^2\kappa _{1} \left( 4+\frac{s^{2}({\bar{x}}y+x{\bar{y}})}{c^2x{\bar{y}}} +\frac{c^{2}({\bar{x}}y+x{\bar{y}})}{s^2x{\bar{y}}}\right) \mathrm {F}(s_a,b), \nonumber \\ {\hat{T}}_{b\pi \pi }^{+-}&= \frac{4}{9}e_d^2\kappa _{1} \left( 4 +\frac{s^{2}({\bar{x}}y+x{\bar{y}})}{c^2{\bar{x}}y} +\frac{c^{2}({\bar{x}}y+x{\bar{y}})}{s^2{\bar{x}}y}\right) \mathrm {F}(s_b,b), \nonumber \\ {\hat{T}}_{c\pi \pi }^{+-}&= -\frac{4}{9}e_ue_d\kappa _{1} \left( 4 -\frac{s^2({\bar{x}}y+x{\bar{y}})}{c^2{\bar{x}}{\bar{y}}} -\frac{c^2({\bar{x}}y+x{\bar{y}})}{s^2xy} \right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\pi \pi }^{+-}&= -\frac{4}{9}e_ue_d\kappa _{1} \left( 4 -\frac{c^2({\bar{x}}y+x{\bar{y}})}{s^2{\bar{x}}{\bar{y}}} -\frac{s^2({\bar{x}}y+x{\bar{y}})}{c^2xy} \right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(47)

and the nonzero twist-3 hard kernels

$$\begin{aligned} {\hat{T}}_{app}^{++}&= -\frac{2}{9}e_u^2\kappa _{2} \left( 2 -\frac{1-{\bar{x}}y}{s^2x{\bar{y}}} -\frac{1-{\bar{x}}y}{c^2x{\bar{y}}}\right) \mathrm {F}(s_a,b),\quad \nonumber \\ {\hat{T}}_{app}^{+-}&= \frac{2}{9}e_u^2\kappa _{2} \left( \frac{1}{s^2c^2} -\frac{2(1-x{\bar{y}})}{{\bar{x}}y}\right) \mathrm {F}(s_a,b),\nonumber \\ {\hat{T}}_{bpp}^{++}&= -\frac{2}{9}e_d^2\kappa _{2} \left( 2 -\frac{1-x{\bar{y}}}{s^2{\bar{x}}y} -\frac{1-x{\bar{y}}}{c^2{\bar{x}}y}\right) \mathrm {F}(s_b,b),\nonumber \\ {\hat{T}}_{bpp}^{+-}&= \frac{2}{9}e_d^2\kappa _{2} \left( \frac{1}{s^2c^2} -\frac{2(1-{\bar{x}}y)}{x{\bar{y}}}\right) \mathrm {F}(s_b,b), \nonumber \\ {\hat{T}}_{cpp}^{++}&= -\frac{2}{9}e_ue_d\kappa _{2} \left( 2+\frac{1-{\bar{x}}{\bar{y}}}{s^2xy} +\frac{1-xy}{c^2{\bar{x}}{\bar{y}}}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_c,b),\nonumber \\ {\hat{T}}_{cpp}^{+-}&= -\frac{2}{9}e_ue_d\kappa _{2} \left( \frac{1}{s^2c^2}-2\right) \mathrm {J}_0(pb)\mathrm {F}(s_c,b),\nonumber \\ {\hat{T}}_{dpp}^{++}&= -\frac{2}{9}e_ue_d\kappa _{2} \left( 2 +\frac{1-{\bar{x}}{\bar{y}}}{c^2xy} +\frac{1-xy}{s^2{\bar{x}}{\bar{y}}} \right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_d,b),\nonumber \\ {\hat{T}}_{dpp}^{+-}&= -\frac{2}{9}e_ue_d\kappa _{2} \left( \frac{1}{s^2c^2}-2\right) \mathrm {J}_0(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(48)
$$\begin{aligned} {\hat{T}}_{cp\sigma }^{++}&=- \frac{1}{27}e_ue_d\kappa _{2} \frac{ \omega b\left( s^2x+c^{2}{\bar{x}}\right) }{scx{\bar{x}}} \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b),\quad \nonumber \\ {\hat{T}}_{cp\sigma }^{+-}&=- \frac{1}{27}e_ue_d\kappa _{2} \frac{ \omega b\left( s^2{\bar{x}}+c^{2}x+1\right) }{scx{\bar{x}}} \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{dp\sigma }^{++}&= -\frac{1}{27}e_ue_d\kappa _{2} \frac{ \omega b\left( c^{2}x+s^2{\bar{x}}\right) }{scx{\bar{x}}} \nonumber \\&\quad \times \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b),\nonumber \\ {\hat{T}}_{dp\sigma }^{+-}&= -\frac{1}{27}e_ue_d\kappa _{2} \frac{\omega b\left( c^{2}{\bar{x}}+s^2x+1\right) }{scx{\bar{x}}} \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(49)
$$\begin{aligned} {\hat{T}}_{ap\sigma ^{\prime }}^{++}&= \frac{1}{27}e_u^2\kappa _{2} \left( \frac{1}{s^2c^2} -\frac{2}{x} \right) \mathrm {F}(s_a,b), \quad \nonumber \\ {\hat{T}}_{ap\sigma ^{\prime }}^{+-}&= \frac{1}{27}e_u^2\kappa _{2} \left( \frac{{\bar{x}}^2}{s^2c^2x{\bar{x}}} -\frac{2}{x{\bar{x}}}\right) \mathrm {F}(s_a,b), \nonumber \\ {\hat{T}}_{bp\sigma ^{\prime }}^{++}&= -\frac{1}{27}e_d^2\kappa _{2} \left( \frac{1}{s^2c^2} -\frac{2}{{\bar{x}}} \right) \mathrm {F}(s_b,b),\nonumber \\ {\hat{T}}_{bp\sigma ^{\prime }}^{+-}&= -\frac{1}{27}e_d^2\kappa _{2} \left( \frac{x^2}{s^2c^2x{\bar{x}}} -\frac{2}{x{\bar{x}}}\right) \mathrm {F}(s_b,b), \nonumber \\ {\hat{T}}_{cp\sigma ^{\prime }}^{++}&= \frac{1}{27}e_ue_d\kappa _{2} \left( \frac{s^2-c^2}{s^2c^2} -\frac{x-{\bar{x}}}{x{\bar{x}}}\right) \mathrm {J}_0(-pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{cp\sigma ^{\prime }}^{+-}&= \frac{1}{27}e_ue_d\kappa _{2} \left( \frac{s^2x^2-c^2{\bar{x}}^2}{s^2c^2x{\bar{x}}} +\frac{x-{\bar{x}}}{x{\bar{x}}}\right) \nonumber \\&\quad \times \mathrm {J}_0(-pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{dp\sigma ^{\prime }}^{++}&= \frac{1}{27}e_ue_d\kappa _{2} \left( \frac{c^2-s^2}{s^2c^2} -\frac{x-{\bar{x}}}{x{\bar{x}}}\right) \mathrm {J}_0(pb)\mathrm {F}(s_d,b),\nonumber \\ {\hat{T}}_{dp\sigma ^{\prime }}^{+-}&= \frac{1}{27}e_ue_d\kappa _{2} \left( \frac{c^2x^2-s^2{\bar{x}}^2}{s^2c^2x{\bar{x}}} +\frac{x-{\bar{x}}}{x{\bar{x}}}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(50)
$$\begin{aligned} {\hat{T}}_{c\sigma p}^{++}&= \frac{1}{27}e_ue_d\kappa _{2} \frac{ \omega b\left( s^2y+c^{2}{\bar{y}}\right) }{scy{\bar{y}}} \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b),\nonumber \\ {\hat{T}}_{c\sigma p}^{+-}&= \frac{1}{27}e_ue_d\kappa _{2} \frac{ \omega b\left( s^2{\bar{y}}+c^{2}y+1\right) }{scy{\bar{y}}} \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\sigma p}^{++}&= \frac{1}{27}e_ue_d\kappa _{2} \frac{ \omega b\left( c^{2}y+s^2{\bar{y}}\right) }{scy{\bar{y}}} \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b),\nonumber \\ {\hat{T}}_{d\sigma p}^{+-}&= \frac{1}{27}e_ue_d\kappa _{2} \frac{ \omega b\left( c^{2}{\bar{y}}+s^2y+1\right) }{scy{\bar{y}}} \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(51)
$$\begin{aligned} {\hat{T}}_{a\sigma ^{\prime } p}^{++}&= \frac{1}{27}e_u^2\kappa _{2} \left( \frac{1}{s^2c^2}-\frac{2}{{\bar{y}}} \right) \mathrm {F}(s_\mathrm {a},b),\nonumber \\ {\hat{T}}_{a\sigma ^{\prime } p}^{+-}&= \frac{1}{27}e_u^2\kappa _{2} \left( \frac{y^2}{s^2c^2y{\bar{y}}} -\frac{2}{y{\bar{y}}}\right) \mathrm {F}(s_a,b),\nonumber \\ {\hat{T}}_{b\sigma ^{\prime } p}^{++}&= -\frac{1}{27}e_d^2\kappa _{2} \left( \frac{1}{s^2c^2}-\frac{2}{y} \right) \mathrm {F}(s_\mathrm {b},b),\nonumber \\ {\hat{T}}_{b\sigma ^{\prime } p}^{+-}&= -\frac{1}{27}e_d^2\kappa _{2} \left( \frac{{\bar{y}}^2}{s^2c^2y{\bar{y}}} -\frac{2}{y{\bar{y}}}\right) \mathrm {F}(s_b,b), \nonumber \\ {\hat{T}}_{c\sigma ^{\prime } p}^{++}&= -\frac{1}{27}e_ue_d\kappa _{2} \left( \frac{s^2-c^2}{s^2c^2} -\frac{y-{\bar{y}}}{y{\bar{y}}}\right) \mathrm {J}_0(pb)\mathrm {F}(s_c,b),\nonumber \\ {\hat{T}}_{c\sigma ^{\prime } p}^{+-}&= -\frac{1}{27}e_ue_d\kappa _{2} \left( \frac{s^2y^2-c^2{\bar{y}}^2}{s^2c^2y{\bar{y}}} +\frac{y-{\bar{y}}}{y{\bar{y}}}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\sigma ^{\prime } p}^{++}&= -\frac{1}{27}e_ue_d\kappa _{2} \left( \frac{c^2-s^2}{s^2c^2} -\frac{y-{\bar{y}}}{y{\bar{y}}}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_d,b), \nonumber \\ {\hat{T}}_{d\sigma ^{\prime } p}^{+-}&= -\frac{1}{27}e_ue_d\kappa _{2} \left( \frac{c^2y^2-s^2{\bar{y}}^2}{s^2c^2y{\bar{y}}} +\frac{y-{\bar{y}}}{y{\bar{y}}}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(52)
$$\begin{aligned} {\hat{T}}_{c\sigma \sigma }^{+-}&= \frac{1}{81}e_ue_d\kappa _{2} \left( \frac{\omega ^{2}b^2}{xy}+\frac{\omega ^{2}b^2}{{\bar{x}}{\bar{y}}}\right) \mathrm {J}_{2}(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\sigma \sigma }^{+-}&= \frac{1}{81}e_ue_d\kappa _{2} \left( \frac{\omega ^{2}b^2}{xy}+\frac{\omega ^{2} b^2}{{\bar{x}}{\bar{y}}}\right) \mathrm {J}_{2}(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(53)
$$\begin{aligned} {\hat{T}}_{c\sigma \sigma ^{\prime }}^{++}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega b s}{c{\bar{y}}}-\frac{\omega b c}{sy}\right) \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b),\nonumber \\ {\hat{T}}_{c\sigma \sigma ^{\prime }}^{+-}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega bs(1+x)}{c{\bar{x}}{\bar{y}}}-\frac{\omega bc(1+{\bar{x}})}{sxy}\right) \nonumber \\&\quad \times \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\sigma \sigma ^{\prime }}^{++}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega b c}{s{\bar{y}}}-\frac{\omega b s}{cy}\right) \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b),\nonumber \\ {\hat{T}}_{d\sigma \sigma ^{\prime }}^{+-}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega bc(1+x)}{s{\bar{x}}{\bar{y}}}-\frac{\omega bs(1+{\bar{x}})}{cxy}\right) \nonumber \\&\quad \times \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(54)
$$\begin{aligned} {\hat{T}}_{c\sigma ^{\prime }\sigma }^{++}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega b s}{c{\bar{x}}}-\frac{\omega b c}{sx}\right) \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b),\nonumber \\ {\hat{T}}_{c\sigma ^{\prime }\sigma }^{+-}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega bs(1+y)}{c{\bar{x}}{\bar{y}}}-\frac{\omega bc(1+{\bar{y}})}{sxy}\right) \nonumber \\&\quad \times \mathrm {J}_{1}(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\sigma ^{\prime }\sigma }^{++}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega b c}{s{\bar{x}}}-\frac{\omega b s}{cx}\right) \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b),\nonumber \\ {\hat{T}}_{d\sigma ^{\prime }\sigma }^{+-}&= -\frac{1}{162}e_ue_d\kappa _{2} \left( \frac{\omega bc(1+y)}{s{\bar{x}}{\bar{y}}}-\frac{\omega bs(1+{\bar{y}})}{cxy}\right) \nonumber \\&\quad \times \mathrm {J}_{1}(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(55)
$$\begin{aligned} {\hat{T}}_{a\sigma ^{\prime }\sigma ^{\prime }}^{++}&= \frac{1}{162}e_u^2\kappa _{2} \left( \frac{s^{2}(1-{\bar{x}}y)}{c^2x{\bar{y}}} +\frac{c^{2}(1-{\bar{x}}y)}{s^2x{\bar{y}}}\right) \mathrm {F}(s_a,b), \nonumber \\ {\hat{T}}_{b\sigma ^{\prime }\sigma ^{\prime }}^{++}&= \frac{1}{162}e_d^2\kappa _{2} \left( \frac{s^{2}(1-x{\bar{y}})}{c^2{\bar{x}}y} +\frac{c^{2}(1-x{\bar{y}})}{s^2{\bar{x}}y}\right) \mathrm {F}(s_b,b), \nonumber \\ {\hat{T}}_{c\sigma ^{\prime }\sigma ^{\prime }}^{++}&= \frac{1}{162}e_ue_d\kappa _{2} \left( \frac{s^2(1-xy)}{c^2{\bar{x}}{\bar{y}}} +\frac{c^2(1-{\bar{x}}{\bar{y}})}{s^2xy}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\sigma ^{\prime }\sigma ^{\prime }}^{++}&= \frac{1}{162}e_ue_d\kappa _{2} \left( \frac{c^2(1-xy)}{s^2{\bar{x}}{\bar{y}}} +\frac{s^2(1-{\bar{x}}{\bar{y}})}{c^2xy}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_d,b), \end{aligned}$$
(56)
$$\begin{aligned} {\hat{T}}_{a\sigma ^{\prime }\sigma ^{\prime }}^{+-}&= \frac{1}{162}e_u^2\kappa _{2} \left( \frac{s^{2}(1+{\bar{x}}y)}{c^2x{\bar{y}}} +\frac{c^{2}(1+{\bar{x}}y)}{s^2x{\bar{y}}}\right) \mathrm {F}(s_a,b), \nonumber \\ {\hat{T}}_{b\sigma ^{\prime }\sigma ^{\prime }}^{+-}&= \frac{1}{162}e_d^2\kappa _{2} \left( \frac{s^{2}(1+x{\bar{y}})}{c^2{\bar{x}}y} +\frac{c^2(1+x{\bar{y}})}{s^2{\bar{x}}y}\right) \nonumber \\&\quad \times \mathrm {F}(s_b,b), \nonumber \\ {\hat{T}}_{c\sigma ^{\prime }\sigma ^{\prime }}^{+-}&= \frac{1}{162}e_ue_d\kappa _{2} \left( \frac{s^2(1+xy)}{c^2{\bar{x}}{\bar{y}}} +\frac{c^2(1+{\bar{x}}{\bar{y}})}{s^2xy}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_c,b), \nonumber \\ {\hat{T}}_{d\sigma ^{\prime }\sigma ^{\prime }}^{+-}&= \frac{1}{162}e_ue_d\kappa _{2} \left( \frac{c^2(1+xy)}{s^2{\bar{x}}{\bar{y}}} +\frac{s^2(1+{\bar{x}}{\bar{y}})}{c^2xy}\right) \nonumber \\&\quad \times \mathrm {J}_0(pb)\mathrm {F}(s_d,b). \end{aligned}$$
(57)

Here the factor \(\kappa _{2}\) is defined as

$$\begin{aligned} \kappa _{2}=\frac{\mu _{\pi }^2}{\omega ^{2}}\kappa _{1} =\frac{\mu _{\pi }^2}{\omega ^{2}}\alpha \alpha _{s}(t_n)\pi ^{2}f_{\pi }^{2}. \end{aligned}$$
(58)

Compared with the twist-2 hard kernels, the twist-3 ones are easily found to be suppressed by the factor \(\kappa _{2}/\kappa _{1}=\mu _{\pi }^2/\omega ^{2}\). In the above expressions for the \({\hat{T}}^{\lambda _1\lambda _2}_{nij}\), \(\mathrm {J}_0\) represents the Bessel function with the variable \(pb=2\omega scb\) and the function \(\mathrm {F}(s_i,b)\) is defined as

$$\begin{aligned} \mathrm {F}(s_i,b) =\left\{ \begin{array}{ll} 2\pi \mathrm {H}_0^{(1)}(\sqrt{s_i}b) &{} \quad {\text{ for }\quad s_i>0}\\ \\ -4i \mathrm {K}_0(\sqrt{-s_i}b) &{} \quad {\text{ for }\quad s_i<0} \end{array} \right. \,. \end{aligned}$$
(59)

The renormalization scales \(t_n\) (\(n=a,b,c,d\)), entering \({\hat{T}}_H\) as the arguments of strong coupling constant \(\alpha _s\) and depending on the kinematics of the specific group, are chosen as

$$\begin{aligned} t_a&=\mathrm {max}\left\{ 2\omega \sqrt{{\bar{x}}y},1/b\right\} , \quad t_b=\mathrm {max}\left\{ 2\omega \sqrt{x{\bar{y}}},1/b\right\} , \nonumber \\ t_c&=\mathrm {max}\left\{ 2\omega \sqrt{{\bar{x}}y-c^{2}{\bar{x}}-s^{2}y},1/b\right\} ,\nonumber \\ t_d&=\mathrm {max}\left\{ 2\omega \sqrt{{\bar{x}}y-s^{2}{\bar{x}}-c^{2}y},1/b\right\} . \end{aligned}$$
(60)

The factors \(s_n\) (\(n=a,b,c,d\)) come from the gluon propagators in each group

$$\begin{aligned} s_a&=4{\bar{x}}y\omega ^2, \quad s_b=4x{\bar{y}}\omega ^2, \nonumber \\ s_c&=4(x-c^2)({\bar{y}}-s^2)\omega ^2, \quad s_d=4(x-s^2)({\bar{y}}-c^2)\omega ^2. \end{aligned}$$
(61)

In addition, it is worth noticing the hard kernels with different helicity have the relations

$$\begin{aligned} {\hat{T}}_{nij}^{++}={\hat{T}}_{nij}^{--},\quad {\hat{T}}_{nij}^{+-}={\hat{T}}_{nij}^{-+}. \end{aligned}$$
(62)

For the \(\gamma \gamma \rightarrow K^+K^-\) process, the hard kernels can be obtained directly with the replacements of \(e_d\rightarrow e_s\), \(f_\pi \rightarrow f_K\), \(\mu _\pi \rightarrow \mu _K\). And the corresponding helicity amplitudes can be expressed as

$$\begin{aligned}&{\mathcal {M}}^{\prime }_{\lambda _1\lambda _2}{(Q,\theta )}\nonumber \\&\quad = \int _0^1\mathrm {d}x\mathrm {d}y\int \frac{b\mathrm {d}b}{(4\pi )^2}\nonumber \\&\qquad \times \sum _{n=a}^{b,c,d}\left( \sum _{i,j=K}^{p,\sigma ,\sigma ^{\prime }}{\hat{\Psi }}_{K}^{i}(1-x,b,1/b) {\hat{T}}^{\lambda _1\lambda _2}_{nij}(x,y,Q,\theta ,b,t_{n}) {\hat{\Psi }}_{K}^{j}\right. \nonumber \\&\qquad \left. \phantom {\left( \sum _{i,j=K}^{p,\sigma ,\sigma ^{\prime }}{\hat{\Psi }}_{K}^{i}(1-x,b,1/b) {\hat{T}}^{\lambda _1\lambda _2}_{nij}(x,y,Q,\theta ,b,t_{n}) {\hat{\Psi }}_{K}^{j}\right. }\times (y,b,1/b)S_t(x)S_t(y)\exp [-S(x,y,Q,b,t_{n})]\right) . \end{aligned}$$
(63)

with

$$\begin{aligned} {\hat{\Psi }}_{K}^{\sigma ^{\prime }}(1-x,{\mathbf {b}}_1,\mu _F)&=\frac{\partial {\hat{\Psi }}_{K}^\sigma (1-x,{\mathbf {b}}_1,\mu _F)}{\partial x},\quad \nonumber \\ {\hat{\Psi }}_{K}^{\sigma ^{\prime }}(y,{\mathbf {b}}_2,\mu _F)&=\frac{\partial {\hat{\Psi }}_{K}^\sigma (y,{\mathbf {b}}_2,\mu _F)}{\partial y}. \end{aligned}$$
(64)

3 Numerical analysis

The differential cross sections of the processes \(\gamma \gamma \rightarrow M^+M^-\) \((M=\pi ,K)\) can be expressed as

$$\begin{aligned} \frac{\mathrm {d}\sigma (\gamma \gamma \rightarrow M^+ M^-)}{\mathrm {d}|\cos \theta |}= \frac{1}{32\pi Q^2}\frac{1}{4}\sum _{\lambda _1,\lambda _2=\pm 1}\mid {\mathcal {M}}_{\lambda _1\lambda _2}\mid ^2. \end{aligned}$$
(65)

In order to make comparison with the experimental measurements, we integrate over the scattering angle in the region \(|\cos \theta |<0.6\) to get the cross sections \(\sigma _0\) for both \(\pi ^+\pi ^-\) and \(K^+K^-\) processes. In this work, we focus on the intermediate energy region \(1.0~\mathrm {GeV}<Q<7.0~\mathrm {GeV}\) to check the applicability of the perturbative QCD in \(\gamma \gamma \rightarrow \pi ^{+}\pi ^{-},~K^{+}K^{-}\) processes.

Table 1 The nonperturbative input parameters of the pion and kaon distribution amplitudes in our calculations
Full size table

In one-loop accuracy, the QCD running coupling is given by \(\alpha _s(\mu ^2)=\pi /[\beta _{0}\ln (\mu ^2/\Lambda _{QCD}^2)]\) with the QCD scale \(\Lambda _{QCD}=0.2\ \mathrm {GeV}\) and the interaction scale \(\mu =t_n\) (\(n=a,b,c,d\)) corresponding to each group in Fig. 1. The most important parameters used in our numerical analysis are listed in Table 1. In addition, the decay constants are taken as \(f_{\pi }=130.4~\mathrm {MeV}\) and \(f_{K}=159.8~\mathrm {MeV}\). For the meson masses and the quark mass entering the pion and kaon distribution amplitudes, we take \(m_\pi =139.6~\mathrm {MeV}\), \(m_K=493.7~\mathrm {MeV}\) and \(m_{s}(2 \,\mathrm {GeV})=95~\mathrm {MeV}\) in \(\overline{\mathrm {MS}}\) scheme. All of the values are quoted from PDG [64]. The Gegenbauer moments \(a_{2,4}^\pi \) and \(a_{1,2}^K\) in the pion and kaon distribution amplitudes come from QCD sum rule [35, 62]. For the chiral enhancement parameters \(\mu _\pi \) and \(\mu _K\), we employ the well known chiral perturbative theory relations [65]

$$\begin{aligned} {\mathcal {R}}&=\frac{2m_{s}}{m_{u}+m_{d}}=24.4\pm 1.5,\quad \quad \nonumber \\ {\mathcal {Q}}^2&=\frac{m_{s}^{2}-(m_{u}+m_{d})^{2}/4}{m_{d}^{2}-m_{u}^{2}}=(22.7\pm 0.8)^{2} \end{aligned}$$
(66)

and obtain

$$\begin{aligned} \mu _\pi =\frac{m_\pi ^2{\mathcal {R}}}{2m_s},\quad \quad \mu _K=\frac{m_K^2}{m_s\left[ 1+\frac{1}{{\mathcal {R}}}\left( 1-\frac{{\mathcal {R}}^2-1}{4{\mathcal {Q}}^2}\right) \right] }. \end{aligned}$$
(67)

The remaining parameters of the twist-3 distribution amplitudes in our calculations are taken from Ref. [45] and shown in Table 1 for brevity.

Table 2 Gegenbauer moments of five sample models of the pion and kaon distribution amplitudes at the scale \(\mu _0=1\ \mathrm {GeV}\)
Full size table
Fig. 2
figure 2

Twist-2 results of the cross sections \(\sigma _{0}(\pi ^{+}\pi ^{-})\) and \(\sigma _{0}(K^{+}K^{-})\) with the five sample models of the distribution amplitudes listed in Table. 2. The points with errors are the experiment data from Refs. [12, 13, 15]

Full size image
Fig. 3
figure 3

Twist-3 results of the cross sections \(\sigma _{0}(\pi ^{+}\pi ^{-})\) and \(\sigma _{0}(K^{+}K^{-})\) with the five sample models of the distribution amplitudes listed in Table. 2. The points with errors are the experiment data from Refs. [12, 13, 15]

Full size image

The theoretical uncertainty in this work mainly comes from the nonperturbative inputs of meson distribution amplitudes: one is the Gegenbauer moments \(a_n^M\) and the other is the chiral enhancement parameters \(\mu _M\) (\(n=2,\ 4\) for pion and \(n=1,\ 2\) for kaon, \(M=\pi ,\ K\)). In Table 2, we present five different models of the distribution amplitudes. And the corresponding Gegenbauer moments are in the region which can cover the ones given in the recent lattice determinations [66].

Fig. 4
figure 4

Twist-3 results of the cross sections \(\sigma _{0}(\pi ^{+}\pi ^{-})\) and \(\sigma _{0}(K^{+}K^{-})\) with uncertainties arising from the chiral enhancement parameters \(\mu _{M}\)

Full size image
Fig. 5
figure 5

Cross sections for \(\gamma \gamma \rightarrow \pi ^+\pi ^-\) and \(\gamma \gamma \rightarrow K^+K^-\). Red dotted lines: the twist-2 results in the collinear factorization; Magenta dot-dashed lines: the twist-2 results in the \(k_T\) factorization; Purple solid lines: the twist-3 results in the \(k_T\) factorization. The points with errors are the experiment data from TPC [12], BELLE [15] and ALEPH [13]

Full size image

With the five models of the pion and kaon distribution amplitudes, the cross sections \(\sigma _0(M^{+}M^{-})\) at twist-2 and twist-3 levels are illustrated in Figs. 2 and 3 respectively. For the \(\pi ^{+}\pi ^{-}\) cross sections shown in Fig. 2, one can find that the lines of model I, IV and V with \(a_{2}^{\pi }+a_{4}^{\pi }\) close to the same value (\(\sim 0.23\)) almost coincide with each other. And the line of model II (III) with the smallest (largest) \(a_{2}^{\pi }\) and \(a_{4}^{\pi }\) have the largest (smallest) slope.Footnote 1 It indicates that the twist-2 result of \(\sigma _0(\pi ^{+}\pi ^{-})\) depends on the Gegenbauer momentums almost in the combination of \(a_{2}^{\pi }+a_{4}^{\pi }\). Moreover, by fixing \(a_{2}^{\pi }\) (\(a_{4}^{\pi }\)), i.e., comparing the result of model II with that of model IV (V), the slope of the pion lines is found to become large as \(a_{4}^{\pi }\) (\(a_{2}^{\pi }\)) decrease. The same conclusion can also be obtained by comparing the result of model III with that of model V (IV). While, for the \(K^{+}K^{-}\) cross sections shown in Fig. 2, one can find that the lines of model II and V (III and IV) almost coincide with each other, which implies the twist-2 result of \(\sigma _0(K^{+}K^{-})\) is insensitive to the variations of \(a_{1}^{K}\). Furthermore, the lines of model II and V (III and IV) with the smallest (largest) \(a_{2}^{K}\) have the largest (smallest) slope, i.e., the slope of the kaon lines become large as \(a_{2}^{K}\) decrease. However, with all the five distribution amplitudes, we find that the twist-2 result of \(\sigma _{0}(K^{+}K^{-})\) is several times smaller than its experiment data [12, 13, 15], and the twist-2 result of \(\sigma _{0}(\pi ^{+}\pi ^{-})\) is almost an order of magnitude smaller than the data [12, 13, 15]. Similar conclusion was already drawn in Refs. [27, 28].

At twist-3 level, to assess the uncertainties related to the Gegenbauer moments, we draw the figures at specific chiral enhancement parameters. From Figs. 2 and 3, one can see that the relative uncertainties come from the Gegenbauer moments in the twist-3 results are much smaller than that in the twist-2 results. With the Gegenbauer moments chosen at their central values and the chiral enhancement parameters being in their reasonable ranges, the twist-3 cross sections are reshown in Fig. 4. Comparing Fig. 3 with Fig. 4, it is found that the main uncertainties in the twist-3 contributions come from the chiral enhancement parameters. For both the \(\pi ^{+}\pi ^{-}\) and \(K^{+}K^{-}\) processes, the twist-3 cross sections are found to be in good agreement with the BELLE measurements [15] in the energy region \(2.4~\mathrm {GeV}<Q<4.1~\mathrm {GeV}\) and the ALEPH measurements [13] in the energy region \(2.0~\mathrm {GeV}<Q<6.0~\mathrm {GeV}\). Especially, when the chiral enhancement parameters are taken the upper value \(\mu _{\pi }(2\ \mathrm {GeV})=2.80~\mathrm {GeV}\) and \(\mu _{K}(2\ \mathrm {GeV})=2.75~\mathrm {GeV}\), the agreements are remarkable. But, in the relatively low energy region \(1.0~\mathrm {GeV}<Q<2.0~\mathrm {GeV}\), there still exists considerable discrepancies between our results and the experiment data [12]. For the \(\pi ^{+}\pi ^{-}\) process, the discrepancy in \(1.0~\mathrm {GeV}<Q<2.0~\mathrm {GeV}\) may be ascribed to the interference of the continuum with the resonances, such as the \(f_{2}(1270)\). For the \(K^{+}K^{-}\) process, the neglection of the twist-4 contributions, which are suppressed by the factor \(m_{K}^{2}/Q^{2}\), may lead to the discrepancy in \(1.0~\mathrm {GeV}<Q<2.0~\mathrm {GeV}\).

In Fig. 5, we make a comparison between the twist-2 and the twist-3 results of the cross sections \(\sigma _{0}(\pi ^{+}\pi ^{-})\) and \(\sigma _{0}(K^{+}K^{-})\) with all the nonperturbative input parameters chosen at the central values. Here we should note that the twist-2 results in the collinear factorization could be enhanced by about 2–3 times if modern distribution amplitudes are used, which would be similar with the situation in the \(k_{T}\) factorization (shown in Fig. 2). Compared with the previous twist-2 results [19] obtained in the collinear factorization, the twist-2 results in the \(k_T\) factorization are enhanced several times in the energy region \(2.0~\mathrm {GeV}<Q<7.0~\mathrm {GeV}\), but suppressed significantly in the relatively low energy region \(1.0~\mathrm {GeV}<Q<2.0~\mathrm {GeV}\). The enhancement in \(2.0~\mathrm {GeV}<Q<7.0~\mathrm {GeV}\) may be due to the higher-power corrections from the transverse momentum \({\mathbf {k}}_{\perp }\). While the suppression in \(1.0~\mathrm {GeV}<Q<2.0~\mathrm {GeV}\) may be ascribed to the corrections from the sudakov resummation, which have been organized into the suppression factor \(\mathrm {exp}[-S]\). As pointed out in Ref. [24], the asymptotic scattering amplitudes for the processes \(\gamma \gamma \rightarrow \pi ^{+}\pi ^{-},~K^{+}K^{-}\) are insensitive to the Sudakov corrections. It indicates that the Sudakov factor \(\mathrm {exp}[-S]\) affects the cross sections slightly in the relatively high energy region, but may lead to a strong suppression at the relatively low energy scale. Comparing the twist-2 results with the twist-3 ones in the \(k_{T}\) factorization, one can conclude that the twist-3 corrections and their interference with the \({\mathbf {k}}_{\perp }\) effects are very significant for both the \(\pi ^{+}\pi ^{-}\) and \(K^{+}K^{-}\) processes in the intermediate energy region \(1.0~\mathrm {GeV}<Q<7.0~\mathrm {GeV}\). Especially in the relatively low energy region \(1.0~\mathrm {GeV}<Q<2.0~\mathrm {GeV}\), the twist-3 results of \(\sigma _{0}(\pi ^+\pi ^-)\) and \(\sigma _{0}(K^+K^-)\) are enhanced by almost an order of magnitude as compared with the twist-2 results. Similar situations can also be found in the calculations of the pion-photon transition form factor [59] and the pion electromagnetic form factor [37, 39, 55]. A more detailed investigation has shown that the twist-3 corrections fall off rapidly with increasing Q and, beyond \(10~\mathrm {GeV}\) region for both pion and kaon, fall below the twist-2 contributions. As is known that, the twist-2 contributions are expected to dominate in the cross section at the asymptotically large momentum transfers. However, as evident from Fig. 5, the twist-3 contributions should be taken into account in the intermediate energy region \(1.0~\mathrm {GeV}<Q<7.0~\mathrm {GeV}\). At this moment, one may worry about possible contributions from the three-parton Fock state, which can also contribute to the cross sections at twist-3 level. As pointed out in Refs. [38, 40, 46, 47], the three-parton twist-3 contributions are strongly suppressed by the factor \(f_{3M}/(f_{M}\mu _{M})\) (\(M=\pi ,K\)) and at least an order of magnitude smaller than the two-parton twist-3 contributions for the time-like pion and kaon electromagnetic form factors in the intermediate energy region. Due to the similarity of the calculationsFootnote 2 between the helicity amplitudes of the two-photon process and the time-like electromagnetic form factors, one can neglect the three-parton contributions safely in \(\gamma \gamma \rightarrow \pi ^{+}\pi ^{-},~K^{+},K^{-}\) processes.

Fig. 6
figure 6

Cross section ratio \(\sigma _{0}(K^{+}K^{-})/\sigma _{0}(\pi ^{+}\pi ^{-})\). Red dotted line: the twist-2 result in the collinear factorization; Magenta dot-dashed line: the twist-2 result in the \(k_T\) factorization; Purple lines: the twist-3 result in the \(k_T\) factorization. The cyan band indicates the theoretical uncertainty arise from the chiral enhancement parameters \(\mu _{M}\). The experiment data are taken from the collaborations of TPC [12], ALEPH [13] and BELLE [15]

Full size image
Fig. 7
figure 7

Angular distributions \(\sigma _{0}^{-1}\mathrm {d}\sigma /\mathrm {d}|\cos \theta |\) for the processes \(\gamma \gamma \rightarrow M^{+}M^{-}\). Red solid line: the twist-2 results in the collinear factorization; Magenta dashed line: the twist-2 results in the \(k_T\) factorization; Purple solid lines: the twist-3 results in the \(k_T\) factorization. All the nonperturbative input parameters are chosen at their central values. The experimental points are from Ref. [15]

Full size image

The cross section ratio \(\sigma _{0}(K^{+}K^{-})/\sigma _{0}(\pi ^{+}\pi ^{-})\) is presented in Fig. 6. We find that the twist-2 results both in the collinear factorization and in the \(k_T\) factorization are almost equal to \((f_{K}/f_{\pi })^{4}\approx 2.26\). Similar theoretical results have also been given in Refs. [9, 11]. While the fitted result from BELLE measurements [15] is \(0.89\pm 0.04\pm 0.15\) for \(3.0~\mathrm {GeV}<Q<4.1~\mathrm {GeV}\) energy region, which is clearly smaller than the twist-2 results obtained in our work and others [9, 11]. Including the twist-3 corrections, our result of the ratio \(\sigma _{0}(K^{+}K^{-})/\sigma _{0}(\pi ^{+}\pi ^{-})\) is found to be in line with the ALEPH measurements [13] in \(2.5~\mathrm {GeV}<Q<4.0~\mathrm {GeV}\) and the BELLE measurements [15] in \(3.5~\mathrm {GeV}<Q<4.1~\mathrm {GeV}\). In the energy region \(1.0~\mathrm {GeV}<Q<2.5~\mathrm {GeV}\), there still exists discrepancy between our prediction and the experimental measurements. The reason may be due to the contributions from the resonances and the \(m_{M}^{2}/Q^{2}\) terms, which have been neglected in our calculations, may play a significant role in this energy region. Another interesting issue we should note here, is related to the cross section ratio between the neutral and charged channels, such as the ratios \(\sigma _{0}(\pi ^{0}\pi ^{0})/\sigma _{0}(\pi ^{+}\pi ^{-})\) and \(\sigma _{0}(K^{0}_{S}K^{0}_{S})/\sigma _{0}(K^{+}K^{-})\), which exhibit the difference of these two types of cross sections on the energy dependencies. In literature, these ratios have been predicted by different methods, such as the perturbative QCD [9] and the handbag model [67, 68]. However, the predictions from both two methods are inconsistent with the experimental measurements [69, 70]. More discussions about this issue can also be found in Refs. [6, 7, 71]. In this work, one can see that the twist-3 hard kernels shown in Eqs. (48)–(57) bring new energy dependence into the cross sections. Moreover, the Feynman diagrams in groups \({\mathbf {a}}\) (\({\mathbf {b}}\)) make contributions to the hard kernels with \(e_{u}^{2}\) (\(e_{s}^{2}\)) for the \(K^{+}K^{-}\) channel, and with \(e_{d}^{2}\) (\(e_{s}^{2}\)) for the \(K^{0}_{S}K^{0}_{S}\) channel. While the Feynman diagrams in groups \({\mathbf {c}}\) and \({\mathbf {d}}\) make contributions to the hard kernels with \(e_{u}e_{s}=-2/9\) for the \(K^{+}K^{-}\) channel, and with \(e_{d}e_{s}=1/9\) for the \(K^{0}_{S}K^{0}_{S}\) channel. It means that \({\mathbf {c}}\) and \({\mathbf {d}}\) diagrams enter the charged channel with a additional minus sign as compared to the neutral channel. And these two points may provide possible explanation about the different energy dependencies between these two types of channels observed by the experimental measurements [69]. Similar analysis can also apply to the \(\pi \pi \) channels [70]. In addition, as pointed out by Brodsky [4, 9], the ratio \(\sigma _{0}(\pi ^{0}\pi ^{0})/\sigma _{0}(\pi ^{+}\pi ^{-})\) is sensitive to the shape of pion distribution amplitude, which can be treated as a possible constraint about the pion distribution amplitude through comparing the theoretical prediction of the ratio with its experimental measurement.

At last but not least, we exhibit the pion and kaon angular distributions, i.e., the differential cross sections \(\sigma _{0}^{-1}\mathrm {d}\sigma (\gamma \gamma \rightarrow M^{+}M^{-})/\mathrm {d}|\cos \theta |\), which have been normalized to the cross section \(\sigma _{0}(M^{+}M^{-})\). Owing to the normalization, the theoretical uncertainties of the pion and kaon angular distributions from the Gegenbauer moments and the chiral enhancement parameters cancel to a large extent. Figure 7 shows our results for \(Q=3.2{-}3.3\ \mathrm {GeV}\) which is in the middle range of the BELLE measurements. One can find the twist-2 results in the collinear factorization and those in the \(k_T\) factorization give nearly the same angular distributions. While the angular distributions with the twist-3 corrections in the \(k_T\) factorization become more steady over the region \(|\cos \theta |<0.6\). However, the agreement between the angular distributions obtained in this work and those of the BELLE measurements [15] is not perfect. The reason may be related to the simplification made in Eq. (38), which is illegal in some angular coverage. In Fig. 7, we also show the known BL result [9], corresponding to the blue dot-dashed line \(1.227/\sin ^{4}\theta \), which is obtained by using the approximate relation in Eq. (1) with \(F_{M}(Q^{2})\approx 0.4~\mathrm {GeV}^{2}/Q^{2}\). However, the CLEO measurements [72] gave a larger form factor \(F_{M}(Q^{2})\approx 1.01~\mathrm {GeV}^{2}/Q^{2}\), which would put the known BL result [9] in question. As a matter of fact, the approximate relation in Eq. (1) was obtained at the twist-2 level, while the twist-3 corrections play a key role in both the two-photon processes and the time-like electromagnetic form factor in the intermediate energy region. It implies that the BL relation shown in Eq. (1) may be not a good approximation in the intermediate energy region.

4 Summary and conclusion

Our work represents the first investigation of the twist-3 corrections to the two-photon processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-,K^+K^-\) in the perturbative QCD approach based on the \(k_{T}\) factorization theorem. The transverse momentum dependence and the resummation effects are included in the perturbative QCD approach. We use the twist-2 and twist-3 light-cone wave functions incorporating transverse degrees of freedom as the nonperturbative dynamical inputs. The nonperturbative contributions from the end-point regions can be effectively suppressed by the Sudakov factor \(\mathrm {exp}[-S]\) and the threshold resummation factor \(S_t(x)\). Consequently, the perturbative QCD calculation becomes more self-consistent and applicable, especially in the few GeV region.

Within the uncertainties from the distribution amplitudes, the twist-2 results of the cross sections \(\sigma _{0}(\pi ^{+}\pi ^{-})\) and \(\sigma _{0}(K^{+}K^{-})\) are much smaller than the experiment data [12, 13, 15]. As shown in our numerical analysis, it is found that both the transverse momentum effects and the twist-3 corrections play a significant role in the two-photon processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-,K^+K^-\) in the intermediate energy region. In the relatively high energy regions, the twist-3 results of the cross sections \(\sigma _{0}(\pi ^{+}\pi ^{-})\), \(\sigma _{0}(K^{+}K^{-})\) and their ratio \(\sigma _{0}(K^{+}K^{-})/\sigma _{0}(\pi ^{+}\pi ^{-})\) are in good agreement with their corresponding experiment data [13, 15]. But in the relatively low energy region, the predicted cross sections and their ratio are still in disagreement with the experimental measurement [12]. From the above analysis, we can conclude that the cross sections for \(\gamma \gamma \rightarrow \pi ^+\pi ^-,K^+K^-\) with angular region \(|\cos \theta |<0.6\) may be dominated by the perturbative QCD contributions when the collision energy \(Q\gtrsim 2~\mathrm {GeV}\). And it is noteworthy that, by analyzing the differential cross sections, the authors in Refs. [25, 26] have concluded that the transition from nonperturbative to perturbative QCD in the processes \(\gamma \gamma \rightarrow \pi ^+\pi ^-,K^+K^-\) is at \(Q\approx 2~\mathrm {GeV}\) and \(\theta \approx 40^{\circ }\). Obviously, these two conclusions are consistent with each other.

However, our results of the pion and kaon angular distributions are different from the BELLE measurements [15]. The reason may be partly due to the simplification made in Eq. (38), which is illegal in some angular coverage. In addition, in the relatively low energy region \(1.0~\mathrm {GeV}<Q<2.0~\mathrm {GeV}\), two-photon processes \(\gamma \gamma \rightarrow \pi ^{+}\pi ^{-},~K^{+}K^{-}\) have been investigated by other methods, such as the QCD sum rule [25, 73] and the chiral perturbation theory [74, 75], which can be seen as the complementation of the perturbative QCD approach for a full understanding of these processes.