1 Introduction

Particle creation from the vacuum by strong external electromagnetic and gravitational fields (sometimes we call this effect a violation of the vacuum stability) has been studied for a long time, see, for example, Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. The effect can be observable if the external fields are sufficiently strong, e.g. the magnitude of an electric field should be comparable with the Schwinger critical field \(E_{\mathrm {c}}=m^{2}c^{3}/e\hslash \simeq 10^{16}\,\mathrm {V/cm}\). Nevertheless, recent progress in laser physics allows one to hope that an experimental observation of the effect can be possible in the near future, see Refs. [16,17,18,19,20] for a review. Moreover, electron-hole pair creation from the vacuum becomes also an observable in laboratory conditions effect in graphene and similar nanostructures, see, e.g. Refs. [21, 22]. Depending on the strong field structure, different approaches have been proposed for calculating the effect nonperturbatively. When a semiclassical approximation is not applicable, the most consistent consideration is formulated in the framework of a quantum field theory, in particular, in the framework of QED, see Refs. [4,5,6, 14]. A calculation technics is based on the existence of exact solutions of the Dirac equation with the corresponding external field. Until now, there are known only few exactly solvable cases that allow one to apply directly such a technics. In such a way can be calculated particle creation in the constant uniform electric field [1,2,3], in the adiabatic electric field \(E\left( t\right) =E\cosh ^{-2}\left( t/T_{\mathrm {S}}\right) \,\) [23], in the so-called T-constant electric field [10, 24], in a periodic alternating in time electric field [25, 26], in an and exponentially growing and decaying electric fields [27,28,29] (see Ref. [30] for the review), and in several constant inhomogeneous electric fields of similar forms where the time t is replaced by the spatial coordinate x. An estimation of the role of switching on and off effects for the pair creation effect was done in Ref. [31].

Fig. 1
figure 1

The electric field (left panel – red lines) and its potential (right panel – blue lines) for some pulse durations \(\tau _{j}\) and a fixed amplitude E. In both pictures, \(\tau _{1}<\tau _{2}\)

Full size image

In the present article we study the vacuum instability in an inverse square electric field (an electric field that is inversely proportional to time squared); see its exact definition in the next section. This behavior is characteristic for an effective mean electric field in graphene, which is a deformation of the initial constant electric field by backreaction due to the vacuum instability; see Ref. [32]. From the technical point of view, it should be noted that the problem of the vacuum instability caused by a constant electric field in the de Sitter space considered in Refs. [33,34,35,36,37,38,39,40,41,42,43] shares some similarities to the above problem in the Minkowski space-time. In addition, an inverse square electric field is useful to study the one-loop Heisenberg–Euler effective action in the framework of a locally constant field approximation [44]. At last, results of our study allow one to better understand the role of switching on and off effects in the violation of the vacuum stability. In Sect. 2 we present, for the first time, exact solutions of the Dirac and Klein–Gordon equations with the inverse square electric field in the Minkowski space-time. With the help of these solutions, we study in detail the vacuum instability in such a background in the framework of QED with t-electric potential steps, using notation and some technical results of our review article [30]. In particular, differential and total mean numbers of particles created from the vacuum are calculated in Sect. 3 within the slowly varying approximation. The case of an asymmetric configuration of the inverse square electric field is discussed in Sect. 4. In Sect. 5, the inverse square electric fields is used to imitate switching on and off processes. The obtained results are compared with the case when the form of switching on and off is exponential. Sect. 6 contains some concluding remarks.

2 Solutions of wave equations with the background under consideration

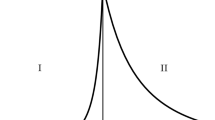
In this section we introduce the time dependent external electric field (in D spatial dimensions), that switches on at the infinitely remote past \( t=-\infty \), switches off at the infinitely remote future \(t=+\infty \) and it is inversely proportional to time squared. In what follows, we call such a field inverse square electric field. The field is homogeneously distributed over space, directed along the axis \(x^{1}=x,\) i.e., \({\mathbf {E}} =(E\left( t\right) ,0,\ldots ,0),\ E^{i}=0\), \(i=2,\ldots ,D\),

$$\begin{aligned} E\left( t\right) =E\left\{ \begin{array}{ll} \left( 1-t/\tau _{1}\right) ^{-2}, &{}\quad t\in {\mathrm {I}}=\left( -\infty ,0\right) , \\ \left( 1+t/\tau _{2}\right) ^{-2}, &{}\quad t\in {\mathrm {II}}=\left[ 0,+\infty \right) . \end{array} \right. \end{aligned}$$
(1)

and is specified by the potentials \(A^{0}=0,\ {\mathbf {A}}=(A_{x}\left( t\right) ,0,\ldots ,0)\), \(\ A^{i}=0\),

$$\begin{aligned} \ A_{x}\left( t\right) =E\left\{ \begin{array}{ll} \tau _{1}\left[ 1-\left( 1-t/\tau _{1}\right) ^{-1}\right] , &{}\quad t\in {\mathrm {I}}, \\ \tau _{2}\left[ \left( 1+t/\tau _{2}\right) ^{-1}-1\right] , &{}\quad t\in {\mathrm {II}}. \end{array} \right. \end{aligned}$$
(2)

The inverse square electric field belongs to the so-called class of t-electric potential steps [30]. It is parameterized by two constants \(\tau _{1,2}\) which play the role of time scales for the pulse durations, respectively. The electric field (1) and its potential (2) are pictured on Fig. 1 for some values of \( \tau _{1,2}\).

For the field under consideration, Dirac spinors in a \(d=D+1\) dimensional Minkowski space-time can always be presented in the following form [10, 30],Footnote 1

$$\begin{aligned}&\psi _{n}\left( x\right) =\left[ i\partial _{t}+H\left( t\right) \right] \gamma ^{0}\exp \left( i\mathbf {pr}\right) \varphi _{n}\left( t\right) v_{\chi ,\sigma }, \nonumber \\&H\left( t\right) =\gamma ^{0}\left\{ \gamma ^{1}\left[ p_{x}-U\left( t\right) \right] +\varvec{\gamma }{\mathbf {p}}_{\perp }+m\right\} , \end{aligned}$$
(3)

where \(v_{\chi ,\sigma }\) is a set of constant and orthonormalized spinors, \( \varphi _{n}\left( t\right) \) is a scalar function, and \(U\left( t\right) =-eA\left( t\right) \) is the potential energy of an electron \(\left( e>0\right) \). The constant spinors obey the identities \(\gamma ^{0}\gamma ^{1}v_{\pm ,\sigma }=\pm v_{\pm ,\sigma }\), \(v_{\chi ,\sigma }^{\dag }v_{\chi ^{\prime },\sigma ^{\prime }}=\delta _{\chi ,\chi ^{\prime }}\delta _{\sigma ,\sigma ^{\prime }}\), in which \(\sigma =\left\{ \sigma _{1},\sigma _{2},\dots ,\sigma _{[d/2]-1}\right\} \) represents a set of eigenvalues of additional spin operators compatible with \(\gamma ^{0}\gamma ^{1}\), while the scalar function \(\varphi _{n}\left( t\right) \) satisfy the second-order ordinary differential equation

$$\begin{aligned}&\left\{ \frac{d^{2}}{dt^{2}}+\left[ p_{x}-U\left( t\right) \right] ^{2}+\pi _{\perp }^{2}-i\chi {\dot{U}}\left( t\right) \right\} \varphi _{n}\left( t\right) =0,\nonumber \\&\quad \pi _{\perp }=\sqrt{{\mathbf {p}}_{\perp }^{2}+m^{2}}. \end{aligned}$$
(4)

Introducing new variables,

$$\begin{aligned} z_{1}\left( t\right)= & {} 2i\omega _{1}\tau _{1}\left( 1-t/\tau _{1}\right) ,\quad t\in {\mathrm {I}}, \nonumber \\ z_{2}\left( t\right)= & {} 2i\omega _{2}\tau _{2}\left( 1+t/\tau _{2}\right) ,\quad t\in {\mathrm {II}}, \end{aligned}$$
(5)

one can reduce Eq. (4) to the Whittaker differential equationFootnote 2 [45, 46, 49]

$$\begin{aligned} \left( \frac{d^{2}}{dz_{j}^{2}}-\frac{1}{4}+\frac{\kappa _{j}}{z_{j}}+\frac{ 1/4-\mu _{j}^{2}}{z_{j}^{2}}\right) \varphi _{n}\left( t\right) =0, \end{aligned}$$
(6)

where

$$\begin{aligned} \kappa _{j}= & {} -\left( -1\right) ^{j}ieE\tau _{j}^{2}\pi _{j}/\omega _{j},\quad \mu _{j}=\left( -1\right) ^{j}\left( ieE\tau _{j}^{2}+\chi /2\right) , \nonumber \\ \omega _{j}= & {} \sqrt{\pi _{j}^{2}+\pi _{\perp }^{2}},\quad \pi _{j}=p_{x}-\left( -1\right) ^{j}eE\tau _{j}. \end{aligned}$$
(7)

A fundamental set of solutions of Eq. (6) can then be represented as a linear combination of Whittaker functions,

$$\begin{aligned}&\varphi _{n}\left( t\right) =b_{1}^{j}W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) +b_{2}^{j}W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right) , \nonumber \\&W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) =e^{-z_{j}/2}z_{j}^{c_{j}/2}\Psi \left( a_{j},c_{j};z_{j}\right) , \nonumber \\&W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right) =e^{-i\pi c_{j}/2}e^{z_{j}/2}z_{j}^{c_{j}/2} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \times \Psi \left( c_{j}-a_{j},c_{j};e^{-i\pi }z_{j}\right) , \end{aligned}$$
(8)

where \(a_{j}=\mu _{j}-\kappa _{j}+1/2\), \(c_{j}=1+2\mu _{j},\) \(b_{1,2}^{j}\) are some arbitrary constants, and \(\Psi \left( a,c;z\right) \) are confluent hypergeometric functions (CHFs) [47].

By definition, the electric field (1) vanishes at the infinitely remote past \(\left( t=-\infty \right) \) and at the infinitely remote future \( \left( t=+\infty \right) \), which means that particles must be free at these limits. From the asymptotic properties of Whittaker functions with large argumentFootnote 3 [49],

$$\begin{aligned}&W_{\kappa ,\mu }\left( z\right) =e^{-z/2}z^{\kappa }\left[ 1+O\left( z^{-1}\right) \right] ,\quad z\rightarrow \infty ,\nonumber \\&\quad \left| \arg z\right| \le 3\pi /2-0^{+}, \end{aligned}$$
(9)

one may classify exact solutions for first \({\mathrm {I}}\) and second II intervals according to their asymptotic behavior as free particles \( \left\{ \, _{+}\varphi \left( t\right) ,\ ^{+}\varphi \left( t\right) \right\} \) or free antiparticles \(\left\{ \, _{-}\varphi \left( t\right) ,\ ^{-}\varphi \left( t\right) \right\} \) as follows:

$$\begin{aligned} \, _{+}\varphi _{n}\left( t\right)= & {} \,_{+}{\mathcal {N}}W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) ,\nonumber \\ \, _{-}\varphi _{n}\left( z_{1}\right)= & {} \,_{-}{\mathcal {N}}W_{\kappa _{1},\mu _{1}}\left( z_{1}\right) ,\quad t\in {\mathrm {I}}, \nonumber \\ \ ^{-}\varphi _{n}\left( t\right)= & {} \,^{-}{\mathcal {N}}W_{-\kappa _{2},\mu _{2}}\left( e^{-i\pi }z_{2}\right) ,\nonumber \\ \ ^{+}\varphi _{n}\left( z_{2}\right)= & {} \,^{+}{\mathcal {N}}W_{\kappa _{2},\mu _{2}}\left( z_{2}\right) ,\quad t\in {\mathrm {II}}. \end{aligned}$$
(10)

Here, the constants\(\, _{\pm }{\mathcal {N}},\ ^{\pm }{\mathcal {N}}\) are conveniently chosen in order to normalize Dirac spinors with respect to the equal-time inner product \(\left( \psi ,\psi ^{\prime }\right) =\int d\mathbf { x}\psi ^{\dagger }\left( x\right) \psi ^{\prime }\left( x\right) \). After the usual volume regularization, we obtain

$$\begin{aligned} \left| \, {}_{\pm }{\mathcal {N}}\right| =\frac{\exp \left( -i\pi \kappa _{1}/2\right) }{\sqrt{2\omega _{1}V_{\left( d-1\right) }q_{1}^{\mp \chi }}},\quad \left| \ ^{\pm }{\mathcal {N}}\right| =\frac{\exp \left( -i\pi \kappa _{2}/2\right) }{\sqrt{2\omega _{2}V_{\left( d-1\right) }q_{2}^{\mp \chi }}}, \end{aligned}$$

where \(q_{j}^{\mp \chi }=\omega _{j}\mp \chi \pi _{j}\) and \(V_{\left( d-1\right) }\) is the volume of the D-dimensional Euclidean space.

With the help of Eq. (10), we use Eq. (3) to introduce IN \( \left\{ \, _{\zeta }\psi \left( x\right) \right\} \) and OUT \(\left\{ \ ^{\zeta }\psi \left( x\right) \right\} \) sets of solutions of Dirac equation corresponding to free electrons \(\left( \zeta =+\right) \) or free positrons \( \left( \zeta =-\right) \) at \(t\rightarrow \pm \infty \). Both sets are related via linear transformations, for instance\(\ ^{\zeta }\psi _{n}\left( x\right) =\sum _{\zeta ^{\prime }}g\left( _{\zeta ^{\prime }}|^{\zeta }\right) \, _{\zeta ^{\prime }}\psi _{n}\left( x\right) \), where coefficients \(g\left( _{\zeta }|^{\zeta ^{\prime }}\right) \) are diagonal \( \left( \, _{\zeta }\psi _{n},\ ^{\zeta ^{\prime }}\psi _{n^{\prime }}\right) =g\left( _{\zeta }|^{\zeta ^{\prime }}\right) \delta _{nn^{\prime }}\) and obey the properties

$$\begin{aligned} g\left( ^{\zeta ^{\prime }}|_{\zeta }\right) ^{*}=g\left( _{\zeta }|^{\zeta ^{\prime }}\right) ,\quad \sum _{\zeta ^{\prime }}g\left( ^{\zeta }|_{\zeta ^{\prime }}\right) g\left( _{\zeta ^{\prime }}|^{\zeta ^{\prime \prime }}\right) =\delta _{\zeta ,\zeta ^{\prime \prime }}. \end{aligned}$$
(11)

This implies decompositions for scalar functions as followsFootnote 4

$$\begin{aligned} \ ^{+}\varphi _{n}\left( t\right)= & {} g\left( _{+}|^{+}\right) \, _{+}\varphi _{n}\left( t\right) +\kappa g\left( _{-}|^{+}\right) \, _{-}\varphi _{n}\left( t\right) , \\ \, _{-}\varphi _{n}\left( t\right)= & {} g\left( ^{+}|_{-}\right) \ ^{+}\varphi _{n}\left( t\right) +\kappa g\left( ^{-}|_{-}\right) \ ^{-}\varphi _{n}\left( t\right) . \end{aligned}$$

Using these decompositions and continuity conditions

$$\begin{aligned} \left. \, _{-}^{+}\varphi _{n}\left( t\right) \right| _{t=0+\varepsilon }= & {} \left. \, _{-}^{+}\varphi _{n}\left( t\right) \right| _{t=0-\varepsilon }, \\ \left. \partial _{t}\, _{-}^{+}\varphi _{n}\left( t\right) \right| _{t=0-\varepsilon }= & {} \left. \partial _{t}\, _{-}^{+}\varphi _{n}\left( t\right) \right| _{t=0+\varepsilon }, \end{aligned}$$

one can calculate basic coefficients,

$$\begin{aligned} g\left( _{-}|^{+}\right)= & {} 2\kappa e^{\frac{i\pi \chi }{2}}e^{i\theta _{+}} \sqrt{\frac{\tau _{1}q_{1}^{+\chi }\tau _{2}}{q_{2}^{-\chi }}}\left( \frac{ \omega _{2}\tau _{2}}{\omega _{1}\tau _{1}}\right) ^{\frac{\chi }{2}}\nonumber \\&\times \, e^{- \frac{\pi }{2}\left( \nu _{1}^{-}+\nu _{2}^{+}\right) }\Delta \left( t\right) \nonumber \\ \Delta \left( t\right)= & {} \Psi \left( a_{2},c_{2};z_{2}\right) f_{1}^{+}\left( t\right) \nonumber \\&+\,\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) f_{2}^{-}(t); \end{aligned}$$
(12)
$$\begin{aligned} g\left( ^{+}|_{-}\right)= & {} 2e^{-\frac{i\pi \chi }{2}}e^{i\theta _{-}}\sqrt{ \frac{\tau _{1}q_{2}^{-\chi }\tau _{2}}{q_{1}^{+\chi }}}\left( \frac{\omega _{2}\tau _{2}}{\omega _{1}\tau _{1}}\right) ^{\frac{\chi }{2}}\nonumber \\&\times \,e^{\frac{\pi }{ 2}\left( \nu _{1}^{+}+\nu _{2}^{-}\right) }{\tilde{\Delta }}(t), \nonumber \\ {\tilde{\Delta }}\left( t\right)= & {} \Psi \left( a_{1},c_{1};z_{1}\right) f_{2}^{+}\left( t\right) \nonumber \\&+\Psi \left( c_{2}-a_{2},c_{2};e^{-i\pi }z_{2}\right) f_{1}^{-}(t). \end{aligned}$$
(13)

Here \(\kappa =+1\),

$$\begin{aligned} \nu _{j}^{\pm }= & {} eE\tau _{j}^{2}\left( 1\pm \frac{\pi _{j}}{\omega _{j}} \right) ,\quad \theta _{\pm }=\pm \left( \omega _{1}\tau _{1}-\omega _{2}\tau _{2}\right) \\&-\,eE\left[ \tau _{1}^{2}\ln \left( 2\omega _{1}\tau _{1}\right) -\tau _{2}^{2}\ln \left( 2\omega _{2}\tau _{2}\right) \right] , \end{aligned}$$

and \(f_{j}^{\pm }\left( t\right) \) are combinations of CHFs and their derivatives

$$\begin{aligned} f_{j}^{+}\left( t\right)= & {} \omega _{j}\left[ \frac{1}{2}\left( 1+\frac{c_{j} }{z_{j}}\right) +\frac{d}{dz_{j}}\right] \nonumber \\&\times \Psi \left( c_{j}-a_{j},c_{j};e^{-i\pi }z_{j}\right) , \nonumber \\ f_{j}^{-}\left( t\right)= & {} \omega _{j}\left[ \frac{1}{2}\left( -1+\frac{ c_{j}}{z_{j}}\right) +\frac{d}{dz_{j}}\right] \Psi \left( a_{j},c_{j};z_{j}\right) . \end{aligned}$$
(14)

It can be seen that the calculated coefficients can be mapped onto one another through the simultaneous exchanges \(p_{x}\rightleftarrows -p_{x}\) and \(\tau _{1}\rightleftarrows \tau _{2}\). For example, taking into account that \(\Psi \left( a_{2},c_{2};z_{2}\right) \rightleftarrows \Psi \left( a_{1}-c_{1}+1,2-c_{1};z_{1}\right) \) and \(\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) \rightleftarrows \Psi \left( 1-a_{2},2-c_{2};e^{-i\pi }z_{2}\right) \) under these exchanges and using some Kummer transformations (see e.g. [47]),

$$\begin{aligned}&\Psi \left( a_{1}-c_{1}+1,2-c_{1};z_{1}\right) =z_{1}^{c_{1}-1}\Psi \left( a_{1},c_{1};z_{1}\right) , \\&\Psi \left( 1-a_{2},2-c_{2};e^{-i\pi }z_{2}\right) =e^{i\pi \left( 1-c_{2}\right) }z_{2}^{c_{2}-1}\Psi \\&\quad \times \left( c_{2}-a_{2},c_{2};e^{-i\pi }z_{2}\right) , \end{aligned}$$

one finds that \(\Delta {(t)}\rightleftarrows e^{i\pi \left( 1-c_{2}\right) }z_{1}^{c_{1}-1}z_{2}^{c_{2}-1}{\tilde{\Delta }}{(t)}\). The latter properties yield the identity

$$\begin{aligned} g\left( _{-}|^{+}\right) \rightleftarrows \kappa g\left( ^{+}|_{-}\right) , \end{aligned}$$
(15)

that shall be useful in the calculation of differential quantities, as discussed below.

3 Quantities characterizing the vacuum instability

The g’s coefficients allow us to find differential mean numbers \(N_{n}^{ \mathrm {cr}}\) of pairs created from the vacuum, the total number N and the vacuum-to-vacuum transition probability \(P_{v}\):

$$\begin{aligned} N_{n}^{\mathrm {cr}}= & {} \left| g\left( _{-}|^{+}\right) \right| ^{2},\quad N^{\mathrm {cr}}=\sum _{n}N_{n}^{\mathrm {cr}}, \end{aligned}$$
(16)
$$\begin{aligned} P_{v}= & {} \exp \left[ \kappa \sum _{n}\ln \left( 1-\kappa N_{n}^{\mathrm {cr} }\right) \right] . \end{aligned}$$
(17)

Once the mean numbers \(N_{n}^{\mathrm {cr}}\) depends on the coefficients given by Eqs. (12) and (13), its calculation can be simplified through the properties given by Eqs. (11) and (15). For example, with \(N_{n}^{\mathrm {cr}}\) calculated for \(p_{x}\) negative, the corresponding expression for \(p_{x}\) positive can be extracted from these results through simple exchanges \(-p_{x}\rightleftarrows p_{x}\) and \(\tau _{1}\rightleftarrows \tau _{2}\). Moreover, note that all results above can be generalized to discuss creation of Klein–Gordon particles from the vacuum. To do so, one has to take into account that \(n={\mathbf {p}}\) and substitute \(\kappa =-1\), \(\chi =0\), \(q_{j}^{\mp \chi }=1\) in all formulas throughout in this article.

3.1 Slowly varying field regime

3.1.1 Differential mean numbers

In this subsection we calculate differential mean numbers of pairs created from the vacuum \(N_{n}^{\mathrm {cr}}\) in the most favorable configuration for particle creation, that is when the external field is sufficiently strong and acts over a sufficiently large time. We call such configuration as slowly varying field, which specified by the following condition

$$\begin{aligned} \min \left( eE\tau _{1}^{2},eE\tau _{2}^{2}\right) \gg \max \left( 1,\frac{ m^{2}}{eE}\right) , \end{aligned}$$
(18)

with \(\tau _{1}/\tau _{2}\) fixed. Within this condition, it is still necessary to compare parameters involving the quantum numbers with the numbers above. To this end, it is meaningful to discuss some general peculiarities underlying the momentum distribution of pairs created by t -electric steps. First, since the electric field is homogeneously directed along the x-direction only, it creates pairs with a wider range of values of \(p_{x}\) instead \({\mathbf {p}}_{\perp }\), once they are accelerated along the direction of the field. Accordingly, one may consider a restricted range of values to \({\mathbf {p}}_{\perp }\), namely \(\sqrt{\lambda }<K_{\perp }\), in which \(K_{\perp }\) is any number within the interval \(\min \left( eE\tau _{1}^{2},eE\tau _{2}^{2}\right) \gg K_{\perp }^{2}\gg \max \left( 1,m^{2}/eE\right) \). As for the longitudinal momentum \(p_{x}\), we restrict subsequent considerations to \(p_{x}\) negative and generalize results for \( p_{x}\) positive using the properties discussed at the end of Sect. 2. Thus, as \(p_{x}\) admits values within the half-infinite interval \(-\infty <p_{x}\le 0\), the kinetic momentum \(\pi _{1}\) varies from large and positive to large and negative values \(eE\tau _{1}\ge \pi _{1}>-\infty \). However, differential mean numbers \(N_{n}^{\mathrm {cr}}\) are significant only in the range \(-\left| \pi _{\perp }\right| \beta _{1}\le \pi _{1}\le eE\tau _{1}\), whose main contributions lies in four specific subranges

$$\begin{aligned}&(\hbox {a}) \ \sqrt{eE}\tau _{1}-\frac{\delta _{1}}{\sqrt{2}}\le \frac{\pi _{1}}{\sqrt{eE}}\le \sqrt{eE}\tau _{1}, \nonumber \\&(\hbox {b}) \ \sqrt{eE}\tau _{1}\left( 1-\Upsilon _{1}\right)<\frac{ \pi _{1}}{\sqrt{eE}}<\sqrt{eE}\tau _{1}-\frac{\delta _{1}}{\sqrt{2}}, \nonumber \\&(\hbox {c}) \ \sqrt{\lambda }\beta _{1}\le \frac{\pi _{1}}{\sqrt{eE}} \le \sqrt{eE}\tau _{1}\left( 1-\Upsilon _{1}\right) ,\nonumber \\&(\hbox {d}) \ \frac{\left| \pi _{1}\right| }{\sqrt{eE}}<\sqrt{\lambda }\beta _{1}, \end{aligned}$$
(19)

wherein \(0<\delta _{1}\ll 1\), \(0<\beta _{1}\ll 1\) and \(\delta _{1}/\sqrt{2} <\Upsilon _{1}\ll 1\) are sufficiently small numbers so that \(\Upsilon _{1} \sqrt{eE}\tau _{1}\) and \(\beta _{1}eE\tau _{1}^{2}\) are finite. To study the mean numbers \(N_{n}^{\mathrm {cr}}\), we conveniently introduce two sets of variables

$$\begin{aligned} \eta _{1}=\frac{e^{-i\pi }z_{1}}{c_{1}},\quad \eta _{2}=\frac{z_{2}}{c_{2}},\quad {\mathcal {Z}}_{j}=\left( \eta _{j}-1\right) {\mathcal {W}}_{j}\sqrt{c_{j}}, \end{aligned}$$
(20)

where \({\mathcal {W}}_{j}=\left| \eta _{j}-1\right| ^{-1}\sqrt{2\left( \eta _{j}-1-\ln \eta _{j}\right) }\), and take into account that \(\pi _{2}\) is large and negative \(\pi _{2}\le -eE\tau _{2}\), which means that \(a_{2}\) is fixed while \(c_{2}\) and \(z_{2}\) are large throughout the ranges above.

The range \((\hbox {a})\) correspond to small values to \(\left| p_{x}\right| /\sqrt{eE}\) and values for \(\eta _{1}\) and \(\eta _{2}\) close to the unity,

$$\begin{aligned} (\hbox {a}) \ 1>\eta _{1}\ge 1-\frac{\delta _{1}}{\sqrt{2eE}\tau _{1}},\quad 1<\eta _{2}\le 1+\frac{\delta _{1}}{\sqrt{2eE}\tau _{2}}, \end{aligned}$$
(21)

so that \({\mathcal {Z}}_{1}\) and \({\mathcal {Z}}_{2}\) are small in this range, \( \left| {\mathcal {Z}}_{j}\right| <\delta _{1}\). As a result, one can use Eq. (66) in Appendix A and the approximations \(\nu _{1}^{-}=\lambda /2\left[ 1+O\left( \left( eE\tau _{1}^{2}\right) ^{-1/2}\right) \right] \), \(\nu _{2}^{+}=\lambda /2\left[ 1+O\left( \left( eE\tau _{2}^{2}\right) ^{-1/2}\right) \right] \) to show that the mean number of pairs created (16) reads

$$\begin{aligned} (\hbox {a}) \ N_{n}^{\mathrm {cr}}\approx e^{-\pi \lambda }, \end{aligned}$$
(22)

in leading-order approximation.Footnote 5 This result coincides with differential number of created particles in a constant electric field [2, 3].

In the range \((\hbox {c})\), \(\left| p_{x}\right| /\sqrt{eE}\) is finite \(\min \left( p_{x}/\sqrt{eE}\right) =-\Upsilon _{1}\sqrt{eE}\tau _{1}\), the variables \(\eta _{j}\) are approximately given by \(\eta _{1}\sim 1-\Upsilon _{1}\), \(\eta _{2}\sim 1+\Upsilon _{1}\tau _{1}/\tau _{2}\) and \( {\mathcal {Z}}_{j}\) are considered large. Thus, one may use the asymptotic approximation given by the second line of Eq. (68) for \(\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) \) and Eq. (67) for \(\Psi \left( a_{2},c_{2};z_{2}\right) \), both in Appendix A, to obtain

$$\begin{aligned} (\hbox {c})\ N_{n}^{\mathrm {cr}}\approx \exp \left( -2\pi \nu _{1}^{-}\right) . \end{aligned}$$
(23)

Note that this distribution tends to the uniform distribution (22) as \(\pi _{1}\rightarrow eE\tau _{1}\left( 1-\Upsilon _{1}\right) \). Equations (22) and (23) are valid both for Fermions as for Bosons.

In the range \((\hbox {d})\), \(\left| p_{x}\right| /\sqrt{eE}\) is large and \(\eta _{2}\) is approximately given by \(\eta _{2}\sim 1+\tau _{1}/\tau _{2}\), so that \({\mathcal {Z}}_{2}\) is large in this interval. Therefore, one may use the same asymptotic approximation for \(\Psi \left( a_{2},c_{2};z_{2}\right) \) as in the range \((\hbox {c})\). As for the Kummer function \(\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) \), it is more convenient to rewrite it in terms of the Whittaker function \( W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) \) through the relation (8) and use the fact that \(z_{1}\left( 0\right) \) and \( \kappa _{1}\) are fixed in this interval, namely \(\min z_{1}\left( 0\right) =2i\sqrt{\lambda }\sqrt{eE}\tau _{1}\) and \(\left| \kappa _{1}\right| \le \beta _{1}eE\tau _{1}^{2}\). As a result, one may use Eq. (71) in A to show that the mean number of pairs created acquires the form

$$\begin{aligned} (\hbox {d}) \ N_{n}^{\mathrm {cr}}\approx \frac{\exp \left( -\pi \nu _{1}^{-}\right) }{\sinh \left( 2\pi eE\tau _{1}^{2}\right) }\times \left\{ \begin{array}{l} \sinh \left( \pi \nu _{1}^{+}\right) ,\quad {\mathrm {Fermi}} \\ \cosh \left( \pi \nu _{1}^{+}\right) ,\quad {\mathrm {Bose}}. \end{array} \right. \end{aligned}$$
(24)

Once the longitudinal kinetic momentum \(\pi _{1}\) is small in this interval and the conditions (18) are satisfied, one may simplify the hyperbolic functions above to obtain \(N_{n}^{\mathrm {cr}}\approx \exp \left( -2\pi \nu _{1}^{-}\right) \) in leading-order approximation. This result agrees with the approximation obtained for the interval \((\hbox {c})\) so that Eq. (23) is uniform over the intervals \((\hbox {c})\) and \(\left( d\right) \). In the intermediate interval \((\hbox {b})\), the differential mean numbers \(N_{n}^{\mathrm {cr}}\) varies between the approximations (22) and (23). At this interval, the Whittaker function \(W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) \) (or \(\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) \)) has to be considered exactly while \(\Psi \left( a_{2},c_{2};z_{2}\right) \) may be approximated by Eq. (63).

Repeating the same considerations above and using the properties of the differential mean numbers \(N_{n}^{\mathrm {cr}}\) under the exchanges \( p_{x}\rightleftarrows -p_{x}\) and \(\tau _{1}\rightleftarrows \tau _{2}\) discussed in the previous section, one may easily generalize results for \( p_{x}\) positive, \(0\le p_{x}<+\infty \). As a result, the mean numbers \( N_{n}^{\mathrm {cr}}\) can be approximated by the asymptotic forms

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx \left\{ \begin{array}{ll} \exp \left( -2\pi \nu _{1}^{-}\right) &{}\quad \hbox {if }-\infty<p_{x}\le 0, \\ \exp \left( -2\pi \nu _{2}^{+}\right) &{}\quad \hbox {if }0<p_{x}<+\infty . \end{array} \right. \end{aligned}$$
(25)

According to the results above, dominant contributions (25) are formed in ranges of large longitudinal kinetic momenta, namely, \(\pi _{\bot }<\pi _{1}\leqslant eE\tau _{1}\) for \(p_{x}<0\) and as \(-eE\tau _{2}<\pi _{2}<-\pi _{\bot }\) for \(p_{x}>0\).

Fig. 2
figure 2

Differential mean number \(N_{n}^{\mathrm { cr}}\) of Fermions created by the symmetric inverse square electric field (1), in which \(\tau _{1}=\tau _{2}\). The exact differential mean numbers (16) are represented by red, brown and yellow solid lines while the asymptotic approximations (23), (25) are represented by dashed color lines. The right panel shows the range of larger discrepancy between exact and asymptotic expressions. All lines labelled with (a), (b) and (c), refers to \(m\tau =10\), 50 and 100, respectively. In both plots, \(E=E_{\mathrm {c}}\) and the horizontal dashed line denotes the uniform distribution \(e^{-\pi \lambda }\)

Full size image

To extend the analysis above to a wider range of values to the longitudinal momentum \(p_{x}\) and compare asymptotic approximations with exact results, it is useful to represent the mean numbers graphically. Thus, in Figs. 2 and 3, we present the differential mean numbers of pairs created from the vacuum \(N_{n}^{\mathrm {cr}}\) given by Eq. (16) as a function of the longitudinal momentum \(p_{x}\) for some values of the pulses duration \(\tau _{j}\) and amplitude E equal to the critical Schwinger value \(E=E_{\mathrm {c}}=m^{2}/e\). In addition, we include the approximations given by Eq. (25) for the same values to the pulses durations \(\tau _{j}\) and amplitude E. In these plots, we set \({\mathbf {p}}_{\perp }=0\) and select for convenience a system of units, in which \(\hslash =c=m=1\). In this system, the reduced Compton wavelength is one unit of length, the Compton time one unit of time and electron’s rest energy \(mc^{2}=1\) one unit of energy. In the plots below, the pulse durations \(\tau _{j}\) and the quantum numbers \(p_{x}\) are dimensionless quantities, relative to electron’s rest mass \(p_{x}/m\) and \(m\tau _{j}\).

Fig. 3
figure 3

Differential mean number \(N_{n}^{\mathrm {cr}}\) of Bosons created by the symmetric inverse square electric field (1), in which \( \tau _{1}=\tau _{2}\). The exact differential mean numbers (16) are represented by blue, purple and pink solid lines while the asymptotic approximations (23), (25) are represented by dashed color lines. The right panel shows the range of larger discrepancy between exact and asymptotic expressions. All lines labelled with (a), (b) and (c), refers to \(m\tau =10\), 50 and 100, respectively. In both plots, \(E=E_{\mathrm {c}}\) and the horizontal dashed line denotes the uniform distribution \(e^{-\pi \lambda }\)

Full size image

According to the above results, the mean number of pairs created \(N_{n}^{ \mathrm {cr}}\) tend to the uniform distribution \(e^{-\pi \lambda }\) as the pulses duration \(\tau _{j}\) increases. This is consistent with the fact that the inverse square electric field (1) tends to a constant electric field (or a T-constant field with T sufficiently large) as the pulses duration \(\tau _{j}\) increases, whose mean numbers are uniform over a sufficiently wide range of values to the longitudinal momentum \(p_{x}\). Therefore, the exact distributions (16) are expected approach to the uniform distribution for sufficiently large values of the pulses duration \( \tau _{j}\). Moreover, it is seen that the exact distributions tends to the uniform distribution for sufficiently small values to the longitudinal momentum \(p_{x}\). This is also in agreement with the asymptotic estimate given by Eq. (22), obtained for \(p_{x}\) sufficiently small. Finally, comparing asymptotic approximations (dashed lines) with exact distributions (solid lines), we conclude that the accuracy of the approximations (25) increase as \(m\tau \) increases. This results from the fact that as \( m\tau \) increases, the parameter \(eE\tau ^{2}\) increases as well. Thus, larger values to \(m\tau \) present a better accuracy. For the values considered above, the lines (a), (b) and (c) correspond to \(eE\tau ^{2}=100\), 2500 and 10,000, respectively.

3.1.2 Total numbers

In this section we estimate the total number of pairs created \(N^{\mathrm {cr} }\) and the vacuum–vacuum transition probability \(P_{v}\) (17) in the slowly varying approximation (18). For t-electric potential steps, the total number of pairs created is proportional to the space time volumeFootnote 6

$$\begin{aligned} N^{\mathrm {cr}}=V_{\left( d-1\right) }n^{\mathrm {cr}},\quad n^{\mathrm {cr}}= \frac{J_{\left( d\right) }}{\left( 2\pi \right) ^{d-1}}\int d{\mathbf {p}} N_{n}^{\mathrm {cr}}, \end{aligned}$$
(26)

so that it is reduced to the calculation of the total density of pairs created \(n^{\mathrm {cr}}\). Similarly to other exactly solvable cases (see Refs. [15, 30]), to evaluate the total density within the slowly varying configuration (18), one may restrict to the calculation of its dominant contribution \({\tilde{n}}^{\mathrm {cr}}\), characterized by an integration domain of the quantum numbers \({\mathbf {p}}\) in which the density is linear in the total increment of the longitudinal kinetic momentum \(\Delta U=e\left| A_{x}\left( +\infty \right) -A_{x}\left( -\infty \right) \right| \). We conveniently denote this domain by \(\Omega \) and express the dominant contribution by \({\tilde{n}}^{ \mathrm {cr}}\), so that the density is approximately given by

$$\begin{aligned} n^{\mathrm {cr}}\approx {\tilde{n}}^{\mathrm {cr}}=\frac{J_{\left( d\right) }}{ \left( 2\pi \right) ^{d-1}}\int _{{\mathbf {p}}\in \Omega }d{\mathbf {p}}N_{n}^{ \mathrm {cr}}. \end{aligned}$$
(27)

The above analysis shows that dominant contributions for mean numbers of created particles by a slowly varying field are formed in ranges of large longitudinal kinetic momenta, restricted values to \({\mathbf {p}}_{\perp }\), and have the asymptotic forms (25). In this case, \(\Omega \) is realized as

$$\begin{aligned} \Omega :\left\{ \pi _{\perp }-eE\tau _{1}\le p_{x}\le -\pi _{\perp }+eE\tau _{2},\quad \sqrt{\lambda }<K_{\perp }\right\} , \end{aligned}$$

so that the dominant density may be expressed as follows:

$$\begin{aligned} {\tilde{n}}^{\mathrm {cr}}= & {} \frac{J_{\left( d\right) }}{\left( 2\pi \right) ^{d-1}}\int _{\sqrt{\lambda }<K_{\perp }}d{\mathbf {p}}_{\perp }\left[ I_{ {\mathbf {p}}_{\perp }}^{\left( 1\right) }+I_{{\mathbf {p}}_{\perp }}^{\left( 2\right) }\right] , \nonumber \\ I_{{\mathbf {p}}_{\perp }}^{\left( 1\right) }= & {} \int _{\pi _{\perp }}^{eE\tau _{1}}d\pi _{1}e^{-2\pi \nu _{1}^{-}},\quad I_{{\mathbf {p}}_{\perp }}^{\left( 2\right) }=\int _{\pi _{\perp }}^{eE\tau _{2}}d\left| \pi _{2}\right| e^{-2\pi \nu _{2}^{+}}.\nonumber \\ \end{aligned}$$
(28)

Performing two additional change of variables \(\lambda s_{1}=2\nu _{1}^{-}\) and \(\lambda s_{2}=2\nu _{2}^{+}\) in \(I_{{\mathbf {p}}_{\perp }}^{\left( 1\right) }\) and \(I_{{\mathbf {p}}_{\perp }}^{\left( 2\right) }\), respectively, and neglecting exponentially small contributions, these integrals can be rewritten as

$$\begin{aligned} I_{{\mathbf {p}}_{\perp }}^{\left( j\right) }=\int _{1}^{\infty }ds_{j}F_{j}\left( s_{j}\right) e^{-\pi \lambda s_{j}},\quad F_{j}\left( s_{j}\right) =\frac{d\left| \pi _{j}\right| }{ds_{j}}, \end{aligned}$$
(29)

whose superior limits \(\lambda s_{j}^{\max }\simeq 4eE\tau _{j}^{2}\) were extended to infinity for convenience. The leading contributions for integrals (29) comes from values near \(s_{j}\rightarrow 1\), in which \(F_{j}\left( s_{j}\right) \approx -\left( eE\tau _{j}\right) /2s_{j}^{3/2}\). Consequently, the leading terms are

$$\begin{aligned} I_{{\mathbf {p}}_{\perp }}^{\left( j\right) }\approx \frac{eE\tau _{j}}{2} e^{-\pi \lambda }G\left( \frac{1}{2},\pi \lambda \right) , \end{aligned}$$
(30)

where \(G\left( \alpha ,x\right) =e^{z}x^{\alpha }\Gamma \left( -\alpha ,x\right) \) and \(\Gamma \left( -\alpha ,x\right) \) is the incomplete gamma function. Neglecting exponentially small contributions, one can extend the integration limit over \({\mathbf {p}}_{\bot }\) in Eq. (28) from \(\sqrt{ \lambda }<K_{\bot }\) to \(\sqrt{\lambda }<\infty \). As a result, the total density of pairs created (28) reads

$$\begin{aligned} {\tilde{n}}^{\mathrm {cr}}\approx & {} r^{\mathrm {cr}}\frac{\Delta U_{\mathrm {is}}}{ eE}\frac{1}{2}G\left( \frac{d-1}{2},\frac{\pi m^{2}}{eE}\right) ,\nonumber \\ r^{ \mathrm {cr}}= & {} \frac{J_{\left( d\right) }\left( eE\right) ^{\frac{d}{2}}}{ \left( 2\pi \right) ^{d-1}}\exp \left( -\frac{\pi m^{2}}{eE}\right) . \end{aligned}$$
(31)

Here \(r^{\mathrm {cr}}\) is rate of pair creation and \(\Delta U_{\mathrm {is} }=e\left| A\left( +\infty \right) \right. \) \(\left. -A\left( -\infty \right) \right| =eE\left( \tau _{1}+\tau _{2}\right) \) denotes the total increment of the longitudinal kinetic momentum for the inverse square electric field. Under these approximations, the vacuum–vacuum transition probability (17) has the form

$$\begin{aligned}&P_{v}\approx \exp \left( -\mu N^{\mathrm {cr}}\right) ,\nonumber \\&\quad \mu =\sum _{l=0}^{\infty }\frac{\left( -1\right) ^{\left( 1-\kappa \right) l/2}\epsilon _{l+1}}{\left( l+1\right) ^{d/2}}\,\exp \left( -l\pi \frac{m^{2} }{eE}\right) , \nonumber \\&\epsilon _{l}=G\left( \frac{d-1}{2},l\pi \frac{m^{2}}{eE}\right) G\left( \frac{d-1}{2},\frac{\pi m^{2}}{eE}\right) ^{-1}, \end{aligned}$$
(32)

in leading-order approximation. It should be noted that Eqs. (31) and (32) can be equivalently obtained from universal forms for slowly varying t-electric potential steps given by in Ref. [15]. Explicitly, one can use the universal form of the dominant density given by Eq. (3.6) in Ref. [15],

$$\begin{aligned} {\tilde{n}}^{\mathrm {cr}}\approx & {} \sum _{j}{\tilde{n}}_{j}^{\mathrm {cr}},\quad {\tilde{n}}_{j}^{\mathrm {cr}}=\frac{J_{\left( d\right) }}{\left( 2\pi \right) ^{d-1}}\int _{t\in D_{j}}dt\left[ eE_{j}\left( t\right) \right] ^{d/2}\nonumber \\&\times \,\exp \left[ -\frac{\pi m^{2}}{eE_{j}\left( t\right) }\right] , \end{aligned}$$
(33)

to show that Eq. (33) coincides with Eq. (31) after a convenient change of variables. Here \(D_{j}=\left\{ D_{1}={{\mathrm {I}}},\ D_{2}= {{\mathrm {II}}}\right\} \) denotes the integration domain for each interval of definition of the electric field (1). This is one more independent confirmation of the universal form for the total number of pairs created from the vacuum by slowly varying backgrounds.

The representation given by Eq. (31) is particularly useful to compare the present results with another exactly solvable examples, for instance a T-constant electric field [10, 24] and a peak electric field [28], whose dominant densities are proportional to the corresponding total increment of the longitudinal kinetic momentum in the slowly varying regime. Recalling the definitions of the T-constant electric field and the peak electric field [10, 28, 30]

$$\begin{aligned} \mathrm {(i)\ }E\left( t\right)= & {} E,\quad t\in \left[ -T/2,T/2\right] , \nonumber \\ \mathrm {(ii)\ }E\left( t\right)= & {} E\left\{ \begin{array}{ll} e^{k_{1}t}, &{}\quad t\in {\mathrm {I}} \\ e^{-k_{2}t}, &{}\quad t\in {\mathrm {II}}, \end{array} \right. \end{aligned}$$
(34)

as well as their corresponding dominant densities of pair creation in the slowly varying approximation

$$\begin{aligned} (\hbox {i})\ {\tilde{n}}^{\mathrm {cr}}= & {} r^{\mathrm {cr}}\frac{\Delta U_{ \mathrm {T}}}{eE},\quad \Delta U_{\mathrm {T}}=eET, \nonumber \\ (\hbox {ii})\ {\tilde{n}}^{\mathrm {cr}}= & {} r^{\mathrm {cr}}\frac{\Delta U_{ \mathrm {p}}}{eE}G\left( \frac{d}{2},\frac{\pi m^{2}}{eE}\right) ,\nonumber \\&\quad \Delta U_{\mathrm {p}}=eE\left( k_{1}^{-1}+k_{2}^{-1}\right) ,\nonumber \\ \end{aligned}$$
(35)

one can establish relations among these fields by which they are equivalent in pair production. For example, equating dominant densities for a given amplitude E and same longitudinal kinetic momentum increments \(\Delta U_{ \mathrm {p}}=\Delta U_{\mathrm {T}}\), we have shown in [15, 24, 30] that the peak electric field is equivalent to a T-constant electric field in pair production, provided that it acts on the vacuum over an effective time duration

$$\begin{aligned} T_{\mathrm {eff}}=\left( k_{1}^{-1}+k_{2}^{-1}\right) G\left( \frac{d}{2}, \frac{\pi m^{2}}{eE}\right) , \end{aligned}$$
(36)

(cf. Eq. (3.26) in [28]). By definition, \(T_{\mathrm {eff}}=T\) for a T-constant field. In other words, a T-constant field acting over the time interval \(T=T_{\mathrm {eff}}\) is equivalent to the peak electric field in pair production. Extending these considerations to the case of the inverse square electric field (1), we obtain the following effective time duration

$$\begin{aligned} T_{\mathrm {eff}}=\frac{\tau _{1}+\tau _{2}}{2}G\left( \frac{d-1}{2},\frac{ \pi m^{2}}{eE}\right) , \end{aligned}$$
(37)

i.e., a T-constant electric field acting on the vacuum over the same effective time duration \(T=T_{\mathrm {eff}}\) is equivalent to the inverse square electric field (1) in pair production.

Comparing the effective time duration for the peak electric field (34) and the inverse square electric field (1), we see that besides similarities among their exact solutions (in both cases the solutions of the Dirac equation are proportional to Kummer functions), they also share common features regarding particle production. These peculiarities suggest a direct comparison between the peak and inverse square electric fields, assuming that both acts over the same time duration \(T_{\mathrm {eff}}\) and have the same amplitude E, namely

$$\begin{aligned} \frac{\tau _{1}+\tau _{2}}{2}= & {} \left( k_{1}^{-1}+k_{2}^{-1}\right) G\left( \frac{d}{2},\frac{\pi m^{2}}{eE}\right) \nonumber \\&\times \,G\left( \frac{d-1}{2},\frac{\pi m^{2} }{eE}\right) ^{-1}, \end{aligned}$$
(38)

so that we obtain a relation between parameters. Let us consider symmetric fields \(\tau _{1}=\tau _{2}=\tau \), \(k_{1}=k_{2}=k\). For weak amplitudes, \( E\ll m^{2}/e\), one can use the asymptotic approximation of the functions above with large argument \(G\left( \alpha ,z\right) \approx z^{-1}e^{-2z}\), \(z\rightarrow \infty \), to obtain \(\tau /2=k^{-1}\). Thus, one may conclude that a symmetric peak field (cf. Eq. (2.4) in [28]) requires only half of the pulse duration of a symmetric inverse square field (1) to be equivalent in pair production. Such a relation does not depend on electron mass, field strength neither space-time dimensions d. For strong amplitudes \(E\gg m^{2}/e\) though, one can restrict to the leading-order approximation of \(G\left( \alpha ,z\right) \) with small argument, \(G\left( \alpha ,z\right) \approx \alpha ^{-1}\), \(z\rightarrow 0\), to show that the latter relation does depend on the space-time dimensions \(\tau /2\approx \left( 1-d^{-1}\right) k^{-1}\). As a result, we see that \(\tau \approx k^{-1}\) for the lowest space-time dimension \(d=2\) and conclude that the relation between \(\tau \) and k varies within the interval \(k^{-1}\le \tau \le 2k^{-1}\), for any amplitude E or space-time dimensions d, provided that both fields acts over the same effective time duration \(T_{\mathrm {eff}}\).

For completeness, it is worth extending the comparison to the level of the vacuum–vacuum transition probability \(P_{v}\). For the peak electric field, this probability is given by

$$\begin{aligned} P_{v}\approx & {} \exp \left( -\mu N^{\mathrm {cr}}\right) ,\quad \mu =\sum _{l=0}^{\infty }\frac{\left( -1\right) ^{\left( 1-\kappa \right) l/2}}{ \left( l+1\right) ^{d/2}}\epsilon _{l+1}^{\mathrm {p}}e^{-\frac{\pi m^{2}}{eE} l}, \nonumber \\ \epsilon _{l}^{\mathrm {p}}= & {} G\left( \frac{d}{2},\frac{\pi m^{2}}{eE} l\right) G\left( \frac{d}{2},\frac{\pi m^{2}}{eE}\right) ^{-1}, \end{aligned}$$
(39)

(cf. Eq. (3.23) in [28]) while for the inverse square electric field it is given by Eq. (32). Thus we see that \(\epsilon _{l}^{ \mathrm {p}}\approx \epsilon _{l}^{\mathrm {is}}\approx 1\) for strong amplitudes \(E\gg m^{2}/e\) and \(\epsilon _{l}^{\mathrm {p}}\approx \epsilon _{l}^{\mathrm {is}}\approx l^{-1}\) for weak ones \(E\ll m^{2}/e\). Accordingly, one may say that the discrepancy between the time-dependence of both fields are not essential for the vacuum–vacuum transition probability, provided that both electric fields have the same amplitude and are equivalent in production. We stress that this fact is not true for all types of time-dependent electric fields. For example, the probability \(P_{v}\) corresponding to a Sauter-type electric field \(E\left( t\right) =E\cosh ^{-2}\left( t/T_{\mathrm {S}}\right) \) [10, 30, 50] differs substantially in comparison to the cases under consideration, even though all of them are equivalent in pair production in what concerns total numbers of pairs created from the vacuum.

4 Asymmetric configuration

In the previous section, the inverse square electric field (1) was treated in a somewhat symmetrical manner, once the pulses duration \(\tau _{1} \) and \(\tau _{2}\) were considered large, approximately equal and with a fixed ratio \(\tau _{1}/\tau _{2}\). Here we supplement the above study with an essentially asymmetrical configuration for the electric field, characterized by a very sharp pulse duration in the first interval \(\mathrm {I }\) while remaining arbitrary in the second interval \({\mathrm {II}}\). In this way, the electric field is mainly defined on the positive half-interval. The present consideration provides insights on switching on or off effects by inverse square electric fields, as shall be discussed below.

The present configuration is specified by small values to \(\tau _{1}\)

$$\begin{aligned} 0\le eE\tau _{1}^{2}\ll \min \left( 1,\frac{m^{2}}{eE}\right) , \end{aligned}$$
(40)

which includes, as a particular case, the inverse square decreasing electric field

$$\begin{aligned}&E\left( t\right) =E\left( 1+t/\tau _{2}\right) ^{-2},\nonumber \\&\quad A_{x}\left( t\right) =E\tau _{2}\left[ \left( 1+t/\tau _{2}\right) ^{-1}-1\right] , \end{aligned}$$
(41)

when \(eE\tau _{1}^{2}=0\). Besides the condition (40), we are interested in a slowly varying configuration for \(t\in {\mathrm {II}}\), which means that the pulse duration scales \(\tau _{1},\tau _{2}\) obeys additional conditions

$$\begin{aligned} eE\tau _{2}^{2}\gg K_{\perp }^{2}\gg \max \left( 1,\frac{m^{2}}{eE}\right) ,\quad \sqrt{eE}\tau _{1}\sqrt{eE}\tau _{2}\ll 1. \end{aligned}$$
(42)

The rightmost inequality implies that the parameter \(\sqrt{eE}\tau _{1}\) is very small, so that the contribution from the first interval \(t\in I\) is negligible for particle creation. To see that, it is sufficient to compare the g-coefficient \(g\left( _{-}|^{+}\right) \) given by Eq. (12) in the limit \(\sqrt{eE}\tau _{1}\rightarrow 0\) with the one computed directly for the inverse square decreasing electric field (41). To this end, one may repeat the same considerations as in Sect. 2 and take into account that the only essential difference between the fields (1) and (41) lies on the interval I, whose exact solutions of Eq. (4) are now plane waves,

$$\begin{aligned} \, _{\pm }\varphi _{n}\left( t\right) =\, _{\pm }{\mathcal {N}}e^{\mp i\omega _{0}t},\quad \omega _{0}=\sqrt{{\mathbf {p}}^{2}+m^{2}},\ t\in {\mathrm {I}}. \end{aligned}$$
(43)

Calculating the corresponding normalization constants\(\, _{\pm }{\mathcal {N}}\) for this case one obtains, after some elementary manipulations, the following form for the g-coefficient \(g\left( _{-}|^{+}\right) \)

$$\begin{aligned} g\left( _{-}|^{+}\right)= & {} \kappa e^{i\pi \left( 1+\chi \right) /4}e^{i\theta _{2}}\sqrt{\frac{q_{0}^{+\chi }}{\omega _{2}q_{2}^{-\chi }\omega _{0}}}\nonumber \\&\times \left( 2\omega _{2}\tau _{2}\right) ^{\left( 1+\chi \right) /2}e^{-\frac{\pi \nu _{2}^{+}}{2}}\Delta _{0}\left( 0\right) , \nonumber \\ \Delta _{0}\left( t\right)= & {} \frac{1}{2}\omega _{0}\Psi \left( a_{2},c_{2};z_{2}\right) +f_{2}^{-}\left( t\right) ,\nonumber \\ q_{0}^{+\chi }= & {} \left. q_{1}^{+\chi }\right| _{\tau _{1}=0},\ \ \theta _{2}=\left. \theta _{+}\right| _{\tau _{1}=0}. \end{aligned}$$
(44)

It can be readily seen that Eq. (44) is a particular case of Eq. (12) when \(\tau _{1}=0\). To demonstrate that, one has to select a particular value to \(\chi \) since the Whittaker functions has different limiting forms as \(z_{1}\rightarrow 0\) for each chosen \(\mu _{1}\). For example, let us consider the Fermi case with the choice \(\chi =-1\). Thus, using the approximations \(\mu _{1}\approx 1/2\), \(\kappa _{1}\approx 0\) and the limiting form given by Eq. (73) in Appendix A, we obtain

$$\begin{aligned}&W_{0,\frac{1}{2}}\left( e^{-i\pi }z_{1}\right) \approx 1,\quad \frac{d}{ dz_{1}}W_{0,\frac{1}{2}}\left( e^{-i\pi }z_{1}\right) \nonumber \\&\quad \approx \frac{1}{2},\quad z_{1}\rightarrow 0, \end{aligned}$$
(45)

and conclude that Eq. (12) coincides with the coefficient (44) under the choices \(\kappa =+1\) and \(\chi =-1\) in leading-order approximation.Footnote 7 As a result, the influence from the first interval \({\mathrm {I}}\) appears only as next-to-leading order corrections, which means that we can study pair creation by the inverse square decreasing electric field (41) rather than by the inverse square field (1) with \(eE\tau _{1}^{2}\) obeying the conditions (40), in leading-order approximation. Therefore, without loss of generality, we shall study particle creation by the field (41). Note that from the property of the differential mean numbers \(N_{n}^{\mathrm {cr}}\) under the exchanges \(p_{x}\rightleftarrows -p_{x}\) and \(\tau _{1}\rightleftarrows \tau _{2}\), the present discussion can be easily generalized to a configuration in which the field is arbitrary during the first interval \({\mathrm {I}}\) but sharp during the second interval \( {\mathrm {II}}\).

As discussed previously, only a limited interval of values of the quantum numbers \({\mathbf {p}}\) contributes significantly to the differential mean numbers \(N_{n}^{\mathrm {cr}}\). Accordingly, the most significant contribution comes from finite values to the perpendicular momenta \(\mathbf {p }_{\perp }\), satisfying \(\sqrt{\lambda }<K_{\perp }\) in which \(K_{\perp }\) is any number within the interval \(eE\tau _{2}^{2}\gg K_{\perp }^{2}\gg \max \left( 1,m^{2}/eE\right) \). As for the longitudinal momentum \(p_{x}\), the most important contribution comes from the range

$$\begin{aligned} \left( {\tilde{c}}\right) \ -\sqrt{eE}\tau _{2}\left( 1-{\tilde{\Upsilon }} _{2}\right) \le \frac{\pi _{2}}{\sqrt{eE}}<-\sqrt{\lambda }, \end{aligned}$$
(46)

where \(0<{\tilde{\Upsilon }}_{2}\ll 1\) is a number such that \(p_{x}/\sqrt{eE}\) is finite, \(\min \left( p_{x}/\sqrt{eE}\right) ={\tilde{\Upsilon }}_{2}\sqrt{eE} \tau _{2}\). In this range, the auxiliary variable \({\mathcal {Z}}_{2}\) defined in Eq. (20) is considered large, since \(\eta _{2}\approx 1-\tilde{ \Upsilon }_{2}\). Using the asymptotic approximation of the CHF given by the first line of Eq. (68) in Appendix A, we find that the differential mean number of particles created takes the form

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx \exp \left( -2\pi \nu _{2}^{+}\right) . \end{aligned}$$
(47)

This result is valid for Fermions and Bosons.

Besides the range above, there are two additional ones

$$\begin{aligned} \left( {\tilde{a}}\right) \ -\frac{{\tilde{\delta }}_{2}}{\sqrt{2}}-\sqrt{eE} \tau _{2}\le & {} \frac{\pi _{2}}{\sqrt{eE}}\le \frac{{\tilde{\delta }}_{2}}{\sqrt{ 2}}-\sqrt{eE}\tau _{2}, \nonumber \\ ({\tilde{b}}) \ -\sqrt{eE}\tau _{2}+\frac{{\tilde{\delta }}_{2}}{ \sqrt{2}}< & {} \frac{\pi _{2}}{\sqrt{eE}}<-\sqrt{eE}\tau _{2}\left( 1-\tilde{ \Upsilon }_{2}\right) , \end{aligned}$$
(48)

in which \(0<{\tilde{\delta }}_{2}\ll 1\) is a small number. In the first interval \(\left( {\tilde{a}}\right) \), \(\eta _{2}\approx 1-{\tilde{\delta }}_{2}/ \sqrt{2eE}\tau _{2}\) and \(\left| {\mathcal {Z}}_{2}\right| \lesssim {\tilde{\delta }}_{2}\) is considered small so that one can use the asymptotic approximation given by Eq. (66) in Appendix A to show that the mean number of electron/positron pairs are given by

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx & {} \frac{1}{2}\left[ 1-\sqrt{1-\exp \left( -2\pi \nu _{2}^{+}\right) }\cos \theta \right] , \nonumber \\ \theta= & {} \frac{\pi }{4}+\arg \Gamma \left( \frac{i\nu _{2}^{+}}{2}\right) -\arg \Gamma \left( \frac{1}{2}+\frac{i\nu _{2}^{+}}{2}\right) . \end{aligned}$$
(49)

A similar expression can be obtained for Klein–Gordon particles. In the interval \(({\tilde{b}})\), the auxiliary variable \({\mathcal {Z}}_{2}\) is finite. Thus, the uniform asymptotic approximation (63) can be used to simplify the CHF \(\Psi \left( a_{2},c_{2};z_{2}\right) \).

The approximation (47) tends to the uniform distribution \(e^{-\pi \lambda }\) in leading-order approximation for sufficiently large and negative longitudinal kinetic momentum \(\pi _{2}\), satisfying \(\pi _{2}/ \sqrt{eE}\gtrsim -\sqrt{eE}\tau _{2}\). This result clearly differs from the approximation (49), obtained from the exact mean number (absolute squared value of Eq. (44)) for the same interval of the longitudinal kinetic momentum \(\pi _{2}\). Such a discrepancy is due to the asymmetrical time-dependence of the electric field, once the asymptotic forms agree mutually as \(p_{x}\) vary over intervals discussed in Sect. 3.1.1 for the inverse square electric field (1), whose temporal dependence is almost symmetric. This indicates a clear difference in how the differential mean numbers \(N_{n}^{\mathrm {cr}}\) of pairs created by an inverse square decreasing electric field (41) are distributed over the quantum numbers when compared to inverse square electric field (1) in the range of large \(\pi _{2}\), although both mean numbers agrees for finite or sufficiently large \(\pi _{2}\), as it follows from the asymptotic forms (25) and (47). To explore these peculiarities, we present in Figs. 4 and 5 the exact mean number of pairs created from the vacuum \(N_{n}^{\mathrm {cr}}\) given by the absolute squared value of Eq. (44) and the asymptotic approximation (47), as a function of the longitudinal momentum \(p_{x}\) for the same values of the of \(\tau _{2}\) and E considered in Sect. 3.1. As before, we set \( {\mathbf {p}}_{\perp }=0\) and select the system in which \(\hslash =c=m=1\).

Fig. 4
figure 4

Differential mean number \(N_{n}^{\mathrm {cr}}\) of Fermions (left panel) and Bosons (right panel) created from the vacuum by an inverse square decreasing electric field (41). The exact differential mean \(N_{n}^{\mathrm {cr}}\) given by the absolute squared value of Eq. (44) are represented by solid lines while the asymptotic approximation (47) are represented by dashed lines. The lines labelled with (a), (b) and (c), refers to \(m\tau _{2}=100\), 50 and 10, respectively. In both plots, \(E=E_{ \mathrm {c}}\) and the horizontal dashed line denotes the uniform distribution \( e^{-\pi \lambda }\) which, in this case, is \(e^{-\pi } \)

Full size image
Fig. 5
figure 5

Differential mean number \(N_{n}^{\mathrm {cr}}\) of Fermions (left panel) and Bosons (right panel) created from the vacuum by an inverse square decreasing electric field (41). The exact differential mean \(N_{n}^{\mathrm {cr}}\) given by the absolute squared value of Eq. (44) are represented by solid lines while the asymptotic approximation (47) are represented by dashed lines. The lines labelled with (a), (b) and (c), refers to \(m\tau _{2}=100\), 50 and 10, respectively. In both plots, \(E=3E_{ \mathrm {c}}\) and the horizontal dashed line denotes the uniform distribution \( e^{-\pi \lambda }\) which, in this case, is \(e^{-\pi /3}\)

Full size image

According to the graphs above, the mean number of pairs created \(N_{n}^{ \mathrm {cr}}\) tends to the uniform distribution \(e^{-\pi \lambda }\) as \(\tau _{2}\) increases. This is not unexpected since the inverse square decreasing electric field (41) tends to a constant field in the limit \(\tau _{2}\rightarrow \infty \); hence the exact mean numbers should approach to the uniform distribution as \(\tau _{2}\) increases. Moreover, for \(\tau _{2}\) fixed, the mean numbers approach to the uniform distribution as the amplitude E increases, as it can be seen comparing the results from Fig. 4 with those of Fig. 5. This is related with the extend of the dimensionless parameter \(eE\tau _{2}^{2}\) and its comparison to the threshold value \(\max \left( 1,m^{2}/eE\right) \): the greater the parameter \( eE\tau _{2}^{2}\) is in comparison to \(\max \left( 1,m^{2}/eE\right) \), the closer the mean numbers \(N_{n}^{\mathrm {cr}}\) approach to the uniform distribution \(e^{-\pi \lambda }\), which is characteristic to constant electric fields (or a T-constant electric field varying slowly in time).

For \(p_{x}\) sufficiently large, the exact results agree with the asymptotic approximation given by Eq. (47), as it can be observed comparing solid and dashed lines. This is a consequence of the fact that there are values of finite longitudinal kinetic momentum \(\pi _{2}\) (\(p_{x}\) finite, range \(\left( {\tilde{c}}\right) \)) in which the mean numbers tend to the asymptotic forms (47) in slowly varying regime. On the other hand, in the range of sufficiently small \(p_{x}\) (or sufficiently large \(\pi _{2}\)), there are deviations between the exact mean numbers and the asymptotic approximations. Such deviations are expected and usually occurs in the range of small \(p_{x}\), as in the case inverse square electric field (1), displayed in Figs. 2 and 3, or peak electric field [29], displayed in Fig. 4 of this reference. We conclude that the approximation of slowly varying regime does not apply uniformly throughout all values of \(p_{x}\) for values of \(eE\tau _{2}^{2}\) considered in the plots above. To be applicable uniformly, larger values of parameters are needed.

The most striking feature of the results displayed above is the presence of oscillations, an absent feature in the case of the inverse square electric field (1); compare Figs. 2, 3 with 4. These oscillations are consequences of an “abrupt” switching on process near \(t=0\) and frequently occurs in these cases, as reported recently by us in [31]. In this work, oscillations around the uniform distribution were found and discussed for the case of a T-constant electric field (that switches-on and off “abruptly” at definite time instants) and an electric field composed by independent intervals, one exponentially increasing, another constant over the duration T and a third one exponentially decreasing. This is an universal feature of “abrupt” switching on or off processes. Moreover, comparing the results displayed in Figs. 4 and 5 we conclude that the oscillations decrease in magnitude as the parameter \( eE\tau _{2}^{2}\) increases. As a result, the mean numbers are expected to become “rectangular” in the limit \(eE\tau _{2}^{2}\rightarrow \infty \).

From the above considerations and the approximations given by Eq. (47), we conclude that the dominant density of pairs created \({\tilde{n}}^{ \mathrm {cr}}\) (27) can be expressed as

$$\begin{aligned} {\tilde{n}}^{\mathrm {cr}}\approx r^{\mathrm {cr}}\frac{\tau _{2}}{2}G\left( \frac{d-1}{2},\frac{\pi m^{2}}{eE}\right) . \end{aligned}$$
(50)

We see that \({\tilde{n}}^{\mathrm {cr}}\) given by Eq. (50) can be obtained from Eq. (31) setting \(\tau _{1}\rightarrow 0\). The vacuum–vacuum transition probability has the form \(P_{v}=\exp \left( -\mu N^{ \mathrm {cr}}\right) \), with \(\mu \) given by Eq. (32).

5 Switching on and off by inverse square electric fields

As an application of the above results, we consider in this section an electric field of special configuration in which inverse square increasing and decreasing electric fields simulate switching on and off processes. This consideration allow us to compare effects with recent results [31], in which a composite electric field of similar form was regarded to study the influence of switching on and off processes in the vacuum.

The field under consideration is composed by three independent intervals, switching on over the first interval \(t\in {\mathrm {I}}=\left( -\infty ,t_{1}\right) \), remains constant over the intermediate interval \(t\in \mathrm {Int}=\left[ t_{1},t_{2}\right] \) and switching off over the last interval \(t\in {\mathrm {II}}=\left( t_{2},+\infty \right) \). The field has the form

$$\begin{aligned} E\left( t\right) =E\left\{ \begin{array}{ll} \left[ 1-\left( t-t_{1}\right) /\tau _{1}\right] ^{-2}, &{}\quad t\in {\mathrm {I}}, \\ 1, &{}\quad t\in {\mathrm {Int}}, \\ \left[ 1+\left( t-t_{2}\right) /\tau _{2}\right] ^{-2}, &{}\quad t\in {\mathrm {II}}, \end{array} \right. \end{aligned}$$
(51)

and, correspondingly, its potential is

$$\begin{aligned} A_{x}\left( t\right) =E\left\{ \begin{array}{ll} \tau _{1}-t_{1}-\tau _{1}\left[ 1-\left( t-t_{1}\right) /\tau _{1}\right] ^{-1}, &{}\quad t\in {\mathrm {I}}, \\ -t, &{}\quad t\in {\mathrm {Int}}, \\ -\tau _{2}-t_{2}+\tau _{2}\left[ 1+\left( t-t_{2}\right) /\tau _{2}\right] ^{-1}, &{}\quad t\in {\mathrm {II}}, \end{array} \right. \end{aligned}$$
(52)

where \(t_{1}<0\) and \(t_{2}>0\) are fixed time instants.

The existence of an intermediate interval in which the field is constant, \( t\in \mathrm {Int}\), does not change the classification of particle and antiparticle states at asymptotic times given by Eq. (10). However, it introduces certain modifications on the variables and parameters of the Whittaker functions, namelyFootnote 8

$$\begin{aligned}&z_{1}\left( t\right) =2i\omega _{1}\tau _{1}\left[ 1-\left( t-t_{1}\right) /\tau _{1}\right] ,\quad t\in {\mathrm {I}}, \\&z_{2}\left( t\right) =2i\omega _{2}\tau _{2}\left[ 1+\left( t-t_{2}\right) /\tau _{2}\right] ,\quad t\in {\mathrm {II}}, \nonumber \end{aligned}$$
(53)

and

$$\begin{aligned} \kappa _{j}= & {} -\left( -1\right) ^{j}eE\tau _{j}^{2}\frac{\Pi _{j}}{\omega _{j}},\quad \Pi _{j}=p_{x}-eE\left[ t_{j}+\left( -1\right) ^{j}\tau _{j}\right] ,\nonumber \\ \omega _{j}^{2}= & {} \Pi _{j}^{2}+\pi _{\perp }^{2}, \end{aligned}$$
(54)

while the parameters \(\mu _{j}\) remains the same as in Eq. (7). Hence, exact solutions of Eq. (4) for the intervals \({\mathrm {I}}\) and \( {\mathrm {II}}\) are Whittaker functions, classified according to Eq. (10) with \(z_{j}\left( t\right) \) and \(\kappa _{j}\) defined by Eqs. (53) and (54). As for the intermediate interval \(t\in \mathrm {Int}\), Dirac spinors are proportional to Weber Parabolic Cylinder functions (WPCFs) [47] once the exact solutions of Eq. (4) are combinations of these functions

$$\begin{aligned} \varphi _{n}\left( t\right)= & {} b_{+}u_{+}\left( {\mathfrak {Z}}\right) +b_{-}u_{-}\left( {\mathfrak {Z}}\right) ,\quad t\in \mathrm {Int,} \nonumber \\ u_{+}\left( {\mathfrak {Z}}\right)= & {} D_{\nu +\left( \chi -1\right) /2}\left( {\mathfrak {Z}}\right) ,\nonumber \\ u_{-}\left( {\mathfrak {Z}}\right)= & {} D_{-\nu -\left( \chi +1\right) /2}\left( i{\mathfrak {Z}}\right) , \end{aligned}$$
(55)

where \(b_{\pm }\) are constants and

$$\begin{aligned}&{\mathfrak {Z}}\left( t\right) =\left( 1-i\right) \xi \left( t\right) ,\quad \xi \left( t\right) =\sqrt{eE}t-\frac{p_{x}}{\sqrt{eE}},\nonumber \\&\quad \nu =\frac{ i\lambda }{2}. \end{aligned}$$
(56)

As a result, one may repeat the same steps as described in Sect. 2 to find the following form to the g-coefficients:

$$\begin{aligned} g\left( _{-}|^{+}\right)= & {} \kappa \sqrt{\frac{q_{1}^{+}}{8eE\omega _{1}q_{2}^{-}\omega _{2}}} \nonumber \\&\qquad \exp \left[ -\frac{i\pi }{2}\left( \kappa _{1}+\kappa _{2}-\nu -\frac{\chi }{2}\right) \right] \nonumber \\&\quad \times \left[ {\mathcal {F}}_{2}^{-}\left( t_{2}\right) {\mathcal {G}} _{1}^{+}\left( t_{1}\right) -{\mathcal {F}}_{2}^{+}\left( t_{2}\right) \mathcal { G}_{1}^{-}\left( t_{1}\right) \right] , \nonumber \\ g\left( ^{+}|_{-}\right)= & {} \sqrt{\frac{q_{2}^{-}}{8eE\omega _{1}q_{1}^{+}\omega _{2}}} \nonumber \\&\quad \exp \left[ -\frac{i\pi }{2}\left( \kappa _{1}+\kappa _{2}-\nu -\frac{\chi }{2}\right) \right] \nonumber \\&\quad \times \left[ {\mathcal {F}}_{1}^{+}\left( t_{1}\right) {\mathcal {G}} _{2}^{-}\left( t_{2}\right) -{\mathcal {F}}_{1}^{-}\left( t_{1}\right) {\mathcal {G}}_{2}^{+}\left( t_{2}\right) \right] . \end{aligned}$$
(57)

Here, \(q_{j}^{\pm }=\omega _{j}\pm \chi \Pi _{j}\) and \({\mathcal {F}}_{j}^{\pm }\left( t\right) \), \({\mathcal {G}}_{j}^{\pm }\left( t\right) \) are combinations between WPCFs and Whittaker functions

$$\begin{aligned} {\mathcal {F}}_{j}^{\pm }\left( t\right)= & {} u_{\pm }\left( {\mathfrak {Z}}\right) \frac{d}{dt}W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) -W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) \frac{d}{dt}u_{\pm }\left( {\mathfrak {Z}}\right) , \nonumber \\ {\mathcal {G}}_{j}^{\pm }\left( t\right)= & {} u_{\pm }\left( {\mathfrak {Z}}\right) \frac{d}{dt}W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right) \nonumber \\&-W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right) \frac{d}{dt}u_{\pm }\left( {\mathfrak {Z}}\right) . \end{aligned}$$
(58)
Fig. 6
figure 6

Differential mean number of Fermions (a) and Bosons (b) created from the vacuum by electric fields. The solid red and blue lines refers to the composite fields (51) and (62), respectively, with \(\tau _{1}=\tau _{2}=\tau \) and \(k_{1}=k_{2}=k\). The dashed green lines refers to the T-constant field while the horizontal ones denotes the uniform distribution \(e^{-\pi \lambda }\). In both graphs, \(m \tau =1\), \(mk^{-1}=1\), \(mT=5\) and \(E=E_{\mathrm {c}}\)

Full size image

On the basis of the results discussed in Sect. 3.1.1 and previous studies on the T-constant field in the slowly varying regime [10, 30], we see if the parameters satisfy

$$\begin{aligned} \min \left( \sqrt{eE}T,eE\tau _{1}^{2},eE\tau _{2}^{2}\right) \gg \max \left( 1,\frac{m^{2}}{eE}\right) , \end{aligned}$$
(59)

the differential mean number of pairs created acquires the asymptotic form

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx \left\{ \begin{array}{ll} \exp \left( -2\pi \nu _{1}^{-}\right) , &{}\quad {\mathrm {for}}\ p_{x}/\sqrt{eE}\le -\sqrt{eE}T/2, \\ \exp \left( -\pi \lambda \right) , &{} \quad {\mathrm {for}}\ \left| p_{x}\right| /\sqrt{eE}<\sqrt{eE}T/2, \\ \exp \left( -2\pi \nu _{2}^{+}\right) , &{} {\mathrm {for}}\ p_{x}/\sqrt{eE} \ge \sqrt{eE}T/2. \end{array} \right. \end{aligned}$$
(60)

Thus, the total dominant density of pairs created in the slowly varying regime is a sum of densities

$$\begin{aligned}&{\tilde{n}}^{\mathrm {cr}}\approx {\tilde{n}}_{{\mathrm {I}}}^{\mathrm {cr}}+{\tilde{n}} _{\mathrm {Int}}^{\mathrm {cr}}+{\tilde{n}}_{{\mathrm {II}}}^{\mathrm {cr}}\nonumber \\&\quad =\left[ T+ \frac{\tau _{1}+\tau _{2}}{2}G\left( \frac{d-1}{2},\frac{\pi m^{2}}{eE} \right) \right] r^{\mathrm {cr}}, \end{aligned}$$
(61)

in agreement to the universal form given by Eq. (33) [15]. In cases beyond slowly varying configurations, i.e. when the conditions (59) are not satisfied for all parameters, the mean numbers \(N_{n}^{\mathrm {cr}}\) must be studied through the exact expressions for the g-coefficients (57) according to the definition (16). Hence, in what follows we present mean numbers \(N_{n}^{\mathrm {cr}}\) of pairs created from the vacuum by the composite field (51) as a function of the longitudinal momentum \(p_{x}\) for some values of the parameters \(\sqrt{eE}\tau _{j}\) and \(\sqrt{eE}T\). Moreover, in order to compare switching on and off effects with an another composite electric field [31]

$$\begin{aligned} E\left( t\right) =E\left\{ \begin{array}{ll} e^{k_{1}\left( t-t_{1}\right) }, &{}\quad t\in {\mathrm {I}}, \\ 1, &{}\quad t\in {\mathrm {Int}}, \\ e^{-k_{2}\left( t-t_{2}\right) }, &{}\quad t\in {\mathrm {II}}, \end{array} \right. \end{aligned}$$
(62)

wherein exponentially increasing and decreasing intervals simulate switching on and off processes and a T-constant field [10, 30] (in which switching on and off processes are absent) we include, in each graph below, mean numbers of pairs created by the field (62) and the T-constant field for some values of the parameters \(\sqrt{eE}k_{j}^{-1}\) and \(\sqrt{eE}T\). As in the previous sections, we set \({\mathbf {p}} _{\perp }=0\) and select the system in which \(\hslash =c=m=1\).

Fig. 7
figure 7

Differential mean number of Fermions (a) and Bosons (b) created from the vacuum by electric fields. The solid red and blue lines refers to the composite fields (51) and (62), respectively, with \(\tau _{1}=\tau _{2}=\tau \) and \( k_{1}=k_{2}=k\). The dashed green lines refers to the T-constant field while the horizontal ones denotes the uniform distribution \(e^{-\pi \lambda }\). In both graphs, \(m\tau =1\), \(mk^{-1}=1\), \(mT=10\) and \(E=E_{\mathrm {c}}\)

Full size image
Fig. 8
figure 8

Differential mean number of Fermions (a) and Bosons (b) created from the vacuum by electric fields. The solid red and blue lines refers to the composite fields (51) and (62), respectively, with \(\tau _{1}=\tau _{2}=\tau \) and \(k_{1}=k_{2}=k\). The dashed green lines refers to the T-constant field while the horizontal ones denotes the uniform distribution \(e^{-\pi \lambda }\). In both graphs, \(m\tau =1\), \(mk^{-1}=1\), \(mT=5\) and \( E=3E_{\mathrm {c}}\)

Full size image
Fig. 9
figure 9

Differential mean number of Fermions (a) and Bosons (b) created from the vacuum by electric fields. The solid red and blue lines refers to the composite fields (51) and (62), respectively, with \(\tau _{1}=\tau _{2}=\tau \) and \(k_{1}=k_{2}=k\). The dashed green lines refers to the T-constant field while the horizontal ones denotes the uniform distribution \(e^{-\pi \lambda }\). In both graphs, \(m\tau =1\), \(mk^{-1}=1\), \(mT=10\) and \( E=3E_{\mathrm {c}}\)

Full size image

According to the graphs above, the differential mean numbers oscillate around the uniform distribution \(e^{-\pi \lambda }\), irrespective the electric field in consideration. This is consistent to asymptotic predictions for the T-constant field, in the sense that the differential mean numbers \(N_{n}^{\mathrm {cr}}\) stabilizes to the uniform distribution \( e^{-\pi \lambda }\) as soon as \(\sqrt{eE}T\) is sufficiently larger than the characteristic values \(\max \left( 1,m^{2}/eE\right) \). Thus, the larger the value of \(\sqrt{eE}T\), the smaller the magnitude of the oscillations. This explains why oscillations are larger in Fig. 6 in which \(\sqrt{eE} T=5\) in comparison to the ones in Fig. 9, in which \(\sqrt{eE}T=10 \sqrt{3}\). Moreover, one can see that the magnitude of oscillations decrease if a constant field is accompanied by switching on and off processes; compare solid and dashed lines. This decrease in the amplitude of the oscillations is a consequence of smoother switching on and off processes. In the case of the composite field (51), the mean numbers are approximated given by the first and third lines of Eq. (60) while the composite field (62), \(N_{n}^{\mathrm {cr}}\approx \exp \left( -2\pi \Xi _{1}^{-}\right) \) for \(p_{x}/\sqrt{eE}\le -\sqrt{eE}T/2\) and \(N_{n}^{\mathrm {cr}}\approx \exp \left( -2\pi \Xi _{2}^{+}\right) \) for \( p_{x}/\sqrt{eE}\ge \sqrt{eE}T/2\), in which \(\Xi _{j}^{\pm }=k_{j}^{-1}\left( \sqrt{{\tilde{\Pi }}_{j}^{2}+\pi _{\perp }^{2}}\pm \tilde{\Pi }_{j}\right) \), \({\tilde{\Pi }}_{j}=p_{x}-\left( -1\right) ^{j}eEk_{j}^{-1}\left( 1+k_{j}T/2\right) \). Accordingly, the exact mean numbers oscillate around these approximations, whose amplitudes decrease as \( eE\tau _{j}^{2}\), \(eEk_{j}^{-2}\) increases. At last, but not least, we see that the mean numbers of pairs created by the composite field (62) oscillate around the uniform distribution less than by the composite field (51), given the same longitudinal kinetic momentum increment of both switching on and off processes, for all values of the parameters under consideration. Based on the values chosen for the parameters, we conclude that the slowly varying regime provides a better approximation to the composite field (62) than for the field (51). However, assuming the same value for E for both composite fields, it is clear that for \(\tau \) sufficiently larger than \(k^{-1}\) (that is, longitudinal kinetic momentum increment of the inverse square fields is larger than one of exponential fields), the opposite situation occurs. The composite electric field (51) and its peculiarities supply our previous studies [31] on the role of switching on and off processes in the vacuum instability.

6 Some concluding remarks

In addition to few known exactly solvable cases in QED with external backgrounds, an inverse square electric field represents one more example where nonperturbative calculations of particle creation effect can be performed exactly. We have presented in detail consistent calculations of zero order quantum effects in the inverse square electric field as well as in a composite electric field of a special configuration, in which the inverse square electric field simulates switching on and off processes. In all these cases we find corresponding in and out exact solutions of the Dirac and Klein–Gordon equations. Using these solutions, we calculate differential mean numbers \(N_{n}^{\mathrm {cr}}\) of Fermions and Bosons created from the vacuum. Differential quantities are considered both exactly and approximately (within the slowly varying regime). In the second case, we studied these distributions as functions on the particle momenta, establishing ranges of dominant contributions and finding corresponding asymptotic representations. In order to be able to compare visually approximate results with exact ones, we compute and analyze plots of differential mean numbers \(N_{n}^{\mathrm {cr}}\) as functions of \(p_{x}\) for some values to the pulse durations \(\tau _{j}\) and for electric field magnitude E equal to the Schwinger’s critical value. The asymptotic representations agree substantially with exact results as the pulse durations increase. Using the asymptotic representations for differential quantities, we compute the total number \(N^{\mathrm {cr}}\) of created pairs the probability \(P_{v}\) for the vacuum remain the vacuum. The results are consistent with universal estimates in the locally constant field approximation. Moreover, comparing the results with dominant densities of pairs created by the T-constant and peak electric fields, we derive an effective time duration of the inverse square electric field and establish relations by which they are equivalent in pair production effect. Assuming that the peak and the inverse square electric fields act on the vacuum over the same effective time, we relate both fields and conclude that the relation between their pulses varies as \(k^{-1}\le \tau \le 2k^{-1}\), for any amplitude E or space-time dimensions d.

To complete the pictures, we consider in Sect. 4 the case of an asymmetrical configuration, in which the field presents a sharp pulse for \( t<0\). In the limit \(\tau _{1}\rightarrow 0\) the corresponding g -coefficients are consistent with g-coefficients calculated in the symmetric case. Analyzing plots of exact calculations, we see that the mean numbers oscillate around their asymptotic approximate values in contrast to the symmetric case were such oscillations are absent; compare Figs. 2, 3 with Fig. 4. These oscillations are attributed to the asymmetrical time dependence of the electric field or, in other words, to the existence of an “abrupt” switching on process near \(t=0\). Moreover, this feature does not depend on the form of external electric field, they can be observed in other cases, for instance in T-constant electric field (see Figs. 6, 7, 8, 9). Thus, we may conclude that the oscillations are universal features of “abrupt” switching on or off processes.

Considering an electric field composed by three parts, two of which are represented by inverse square fields, we calculate relevant g-coefficients for particle creation and discuss approximate expressions for differential quantities. To understand better switching on and off effects, we compare the above case with the case where switching on and off configurations have exponential behavior. Doing this we consider a configuration in which the duration T of the intermediate T -constant electric fields is greater than the duration of the characteristic pulses \(\tau _{j}\) and \(k_{j}^{-1}\). This configuration allows us to analyze how the differential distributions differ from their asymptotic form \(e^{-\pi \lambda }\). According to Figs. 6, 7, 8 and 9, we conclude that the way of switching on and off is essential for application of slowly varying regime approximation. For example, comparing results in the T-constant electric field (dashed lines) for Fermions with ones for composite fields (solid lines) in Fig. 8, we see they are close to results obtained in the slow variation approximation if parameters of composite fields satisfy the condition \(\sqrt{ eE}T\ge 5\sqrt{3}\), \(\sqrt{eE}\tau =\sqrt{eE}k^{-1}=1.\) At the same time, in the case of a T-constant field with \(\sqrt{eE}T=5\sqrt{3}\) it is not true and the corresponding mean numbers \(N_{n}^{\mathrm {cr}}\) deviate substantially from the uniform distribution \(e^{-\pi \lambda }\). For Bosons, one can see that composite fields with \(\sqrt{eE}T=5\sqrt{3}\), \(\sqrt{eE} \tau =\sqrt{eE}k^{-1}=1\) does not allow application of the slow variation approximation, whereas the condition \(\sqrt{eE}T\ge 5\sqrt{3}\) is close to the threshold condition for composite fields for Fermions. One can also see that differential quantities are quite sensitive to the form of switching on and off. For all configurations displayed in Figs. 6, 7, 8 and 9, we see that exponential switching on and off causes smaller oscillations around the uniform distribution in comparison to the inverse square switching on and off.