Exploring the anomalous top–Higgs FCNC couplings at the electron proton colliders

Abstract

We perform an updated analysis on the searches for the anomalous FCNC Yukawa interactions between the top quark, the Higgs boson, and either an up or charm quark ${{tqh,\ q=u,\ c}}$). We probe the observability of the FCNC top–Higgs couplings through the processes ${e^- p\rightarrow \nu _{\mathrm{e}} }\bar{{t}} \rightarrow \nu _{\mathrm{e}} h \bar{{q}}$ signal I) and $e^- p \rightarrow \nu _{\mathrm{e}} h b$ signal II) at the proposed electron proton ep colliders, where the Higgs boson decays to a ${b}\bar{{b}}$ pair. We find that at the high-luminosity ($1\;{ab}^{-1}$) ep colliders where the electrons have a polarization of $80\%$ and electron energy is typical 60 GeV, the 2$\sigma$ upper limits on ${ Br t\rightarrow uh)}$ are $0.15\times 10^{-2}$ $2.9\times 10^{-4}$) at the 7TeV@LHeC 50TeV@FCC-eh) for signal I and $0.15\times 10^{-2}$ $2.2\times 10^{-4}$) for signal II. We also give an estimate on how the sensitivity (taking signal I as example) would change when we reduce the electron beam energy from 60 to 50 GeV or even 40 GeV due to the cost. The conclusion is that the discovery potential is reduced $8.7\%$ ($29.4\%$) if the electron beam changes from 60 to 50 (40) GeV at the 7 TeV LHeC, and $16.8\%$ ($19.8\%$) at the 50 TeV FCC-eh.

1 Introduction

The discovery of the Higgs boson at the Large Hadron Collider LHC) [1, 2] was a major step towards understanding the electroweak symmetry breaking (EWSB) mechanism and marks a new era in particle physics. The precise measurement of the Higgs boson and the top quark properties would provide the possibility of searching for the anomalous flavor changing neutral current (FCNC) Yukawa interactions between them and either an up or charm quark (${ tqh,\ q=u,\ c}$). According to the Standard Model (SM), FCNC processes are forbidden at tree level and very much suppressed at higher orders due to the Glashow–Iliopoulos–Maiani (GIM) mechanism [3]. For instance, the ${t\rightarrow qh\ (q=u,c)}$ branching ratio is of the order of $\sim 10^{-10}$ or even below. In models beyond the SM (BSM), the GIM suppression can be relaxed, yielding effective tqh couplings many orders of magnitude larger than those of the SM and therefore being detectable using current experimental data. Observations of such anomalous top–Higgs couplings would provide a clear signal of new physics. Examples of such model extensions [4] are, for instance, the Minimal Supersymmetric Model (MSSM) with/without R-parity violation [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19], the two Higgs Doublet Model (2HDM) [20,21,22,23,24,25,26,27,28,29,30,31,32,33], the warped extra dimensions model [34, 35], the Alternative Left–Right symmetric Model (ALRM)[36, 37], the Little Higgs with T parity Model (LHT) [38], the Quark Singlet model (QS) [39,40,41].

Searches for the anomalous FCNC top–Higgs couplings have been performed at the LHC, and the direct limits on the branching ratio are set from the collider experiments. The most stringent constraint through direct measurements was reported by the CMS and ATLAS collaborations. They have set upper limits on the FCNC couplings in the top sector through the top pair production, with one top decaying to wb and the other assumed to decay to hq. The w boson is considered decaying leptonically and the Higgs decaying either to two photons [42,43,44,45] or to ${b}\bar{{b}}$ [46, 47]. Combining the analysis of the different Higgs decay channels, corresponding to 20.3 (19.7) $\mathrm{fb}^{-1}$ data at the center-of-mass energy of 8 TeV for ATLAS (CMS), the 95$\%$ confidence level (C.L.) upper limits have been found to be ${ Br t\rightarrow u) \le 4.5 5.5)\times 10^{-3}}$ [42] and ${ Br t\rightarrow ch) \le 4.6 4.0)\times 10^{-3}}$ [48]. In addition to the direct collider measurements, indirect constraints on the anomalous tqh vertex can be obtained from the low-energy measurements in flavor mixing processes, like, for example, the neutral meson oscillations (${K^0}$–$\bar{{K}}^0$, ${B^0}$–$\bar{{B}}^0$ and ${D^0}$–$\bar{{D}}^0$) [49,50,51]. Typically, at one-loop level, the ${D^0}$–$\bar{{D^0}}$ mixing observable can receive sizable contributions with such an nonvanishing flavor violating tqh coupling [51]. Using data observed on ${D}^0$–$\bar{{D^0}}$ mixing, the upper limit of ${Br t\rightarrow qh)\le 5\times 10^{-3}}$ can be obtained. The tqh coupling also affects the ${ Z\rightarrow c\bar{c}}$ decay at the loop level and is therefore constrained by the electroweak precision observables of the Z boson [52]. On the phenomenological side the sensitivity to these non-standard flavor violating couplings in the top sector has been explored in great detail. A lot of work has been done at the LHC, through top pair production [28, 53,54,55,56], single top plus Higgs production [4, 57, 58], and also single top plus W production[59]. Some have been done at the ${ e^+e^-}$ colliders [60,61,62,63,64], and several at the ep colliders [65, 66]. Some other related studies include, for example, Ref. [67], which derives model-independent constraints on the tqh couplings that arise from the bounds on hadronic electric dipole moments.

In the present paper, we perform an update study of the anomalous FCNC Yukawa interactions at the ep colliders. An earlier study was performed in Ref. [65]. There we briefly reviewed the search of this anomalous couplings at the basic parton level. A comparison between different charge current (CC) and neutral current (NC) production channels was provided. We came to the conclusion that the CC induced ${e^- p\rightarrow \nu _{\mathrm{e}}} \bar{{t}} {\rightarrow \nu _{\mathrm{e}} h} \bar{{q}}$ (signal I) production with $\gamma \gamma$, ${b}\bar{{b}}$ pair and $\tau ^+\tau ^-$ decays are the favored candidate channels. The ${H}\rightarrow \gamma \gamma$ channel was chosen because of its demonstrated high importance for inclusive Higgs boson studies, with a rather clean signature at the normal LHC. However, for a Higgs boson mass around 125 GeV, ${ e^- p\rightarrow \nu _{\mathrm{e}} }\bar{{t}} \rightarrow \nu _{\mathrm{e}} h \bar{{q}}$ production with $h\rightarrow \gamma \gamma$ decay at the ep collider, it suffers from its small branching ratio (0.23$\%$); thus it is not the one most favored. For the ${h}\rightarrow \tau ^+\tau ^-$ channel, the $\tau$ event reconstruction is not easy, thus we have not concentrated on this issue at this moment. In this paper we choose the ${ h\rightarrow b}\bar{{b}}$ mode which is more interesting than the other channels. In addition to signal I, we consider a second production ${ e^- p \rightarrow \nu _{\mathrm{e}} h b}$ (signal II). Different from signal I, the tqh couplings mainly come from the single top decays; in signal II, the couplings are induced through light quarks that are directly emitted from the protons. We present the discovery potentials from both channels and compare them with each other.

Our paper is organized as follows: Sect. 2 presents a short description of the anomalous top–Higgs FCNC couplings. Section 3 presents the analysis and numerical results in detail. The subsections include signal and background analysis, simulation and the discovery potential, etc. The discovery potentials are compared with the LHC limits and the other studies. Typically, its dependence on the electron beam energy is also presented due to the cost reason. Finally, we summarize and present our conclusion in the last section.

2 The anomalous top–Higgs FCNC couplings

Considering the FCNC Yukawa interactions in the effective field theory framework, the SM Lagrangian can be extended simply by allowing the following terms:

$$\begin{aligned} {\mathcal {L}} = \kappa _{\mathrm{tuh}} \bar{{t}}{uh} + \kappa _{\mathrm{tch}} \bar{{t}}{ch + h.c.}, \end{aligned}$$

(1)

where $\kappa _{\mathrm{tuh}}$ and $\kappa _{\mathrm{tch}}$ are the real parameters denoting the flavor changing couplings of Higgs to up-type quarks. Now we have $m_\mathrm{t}$ minus $m_\mathrm{h}$ being larger than $m_\mathrm{c}$, $m_\mathrm{u}$ and $m_\mathrm{b}$; therefore, in addition to the usual decay mode $t\rightarrow w^\pm b$, the top quark can also decay into a charm or up quark associated with a Higgs boson. Similarly, the new tqh interactions can also affect the width of the Higgs boson, through its additional decay into an off-shell top, which subsequently leads to a single w, namely, $h\rightarrow u c\ (t^*\rightarrow wb)$ where $t^*$ denotes an off-shell top quark. The total decay width of the top quark $\Gamma _{\mathrm{t}}$) is

$$\begin{aligned} \Gamma _{\mathrm{t}}= & {} \Gamma ^{\mathrm{SM}}_{\mathrm{t}\rightarrow {w}^-\mathrm{b}}+\Gamma _{\mathrm{t}\rightarrow {ch}}+\Gamma _{\mathrm{t}\rightarrow \mathrm{uh}}. \end{aligned}$$

(2)

Here $\Gamma _{\mathrm{t}\rightarrow {w}^-\mathrm{b}}^{\mathrm{SM}}$ is the normal top decay width in the SM. Its analytical formula up to next-to-leading order(NLO) can be found in Ref. [68]. The ${t\rightarrow u(c)h}$ partial decay width is given as [69]

$$\begin{aligned}&{\Gamma _{t\rightarrow u(c)h}} ={\frac{\kappa ^2_{\mathrm{tu(c)h}}}{16\pi } m_\mathrm{t}}\nonumber \\&\quad \times {[(\tau _{\mathrm{u(c)}}+1)^2-\tau ^2_\mathrm{h}] \sqrt{1-(\tau _\mathrm{h}-\tau _{\mathrm{u(c)}})^2}\sqrt{1-(\tau _\mathrm{h}+\tau _{\mathrm{u(c)}})^2}}\nonumber \\ \end{aligned}$$

(3)

where ${\tau _\mathrm{h}=\frac{m_\mathrm{h}}{m_\mathrm{t}}}$, ${\tau _{\mathrm{u(c)}}=\frac{m_{\mathrm{u(c)}}}{m_\mathrm{t}}}$. The total decay width of the Higgs boson($\Gamma _{\mathrm{h}}$) is given by

$$\begin{aligned} \Gamma _\mathrm{h}= & {} \Gamma _{\mathrm{h}}^{\mathrm{SM}} + \Gamma _{\mathrm{h\rightarrow u}(\bar{{\mathrm{t}}}^*\rightarrow \bar{{\mathrm{b}}}{\mathrm{w}}^-)} + \Gamma _{{\mathrm{h}}\rightarrow \bar{{\mathrm{u}}}{(\mathrm{t}^*\rightarrow \mathrm{bw}^+)}}\nonumber \\&\quad + \Gamma _{\mathrm {h\rightarrow c}(\bar{{\mathrm{t}}}^*\rightarrow \bar{{\mathrm{b}}}{\mathrm{w}}^-)} + \Gamma _{{\mathrm{h}}\rightarrow \bar{{\mathrm{c}}}{(\mathrm{t}^*\rightarrow \mathrm{bw}^+)}}. \end{aligned}$$

(4)

Here $\Gamma _{\mathrm{h}}^{\mathrm{SM}}$ is the normal two body Higgs decay width in the SM. The terms related to the Higgs boson three-body decays are numerically estimated with FFL-package [70,71,72,73]. Thus we have ${\Gamma _\mathrm{h} \simeq \Gamma ^{\mathrm{SM}}_\mathrm{h}} + \sum ^{\bar{{\mathrm{t}}}^*\rightarrow \bar{{\mathrm{b}}}\mathrm{w}^-}_{\mathrm{q=u,c}} 0.28 \kappa ^2_{\mathrm{tq}} + \sum ^{\mathrm{t}^*\rightarrow {\mathrm{bw}}^+}_{\mathrm{q=u,c}} 0.28 \kappa ^2_{\mathrm{tq}} \simeq \Gamma ^{\mathrm{SM}}_\mathrm{h} + 0.56\,(\kappa ^2_{\mathrm{tu}} + \kappa ^2_{\mathrm{tc}})$ in unit of MeV. After assuming the top quark decay width is dominated by the SM and neglecting the light quark mass, the branching ratio for ${t \rightarrow qh}$ is then approximately given by

$$\begin{aligned}&{B(t\rightarrow u(c)h)} \nonumber \\&\quad \mathrm {= \frac{\kappa _{\mathrm{tu(c)h}}^2}{\sqrt{2} G_\mathrm{F} m_\mathrm{t}^2 }} \frac{(1-\tau _\mathrm{h}^2)^2}{(1-\tau _\mathrm{w}^2)^2(1+2 \tau _\mathrm{w}^2)} K_{\mathrm{QCD}} \simeq 0.58\kappa ^2_{\mathrm{tu(c)h}} \end{aligned}$$

(5)

where ${ \tau _\mathrm{w}=\frac{m_\mathrm{w}}{m_\mathrm{t}}}$ and $\mathrm {G_\mathrm{F}}$ is the fermi constant. The factor ${ K_{\mathrm{QCD}}}$ is the NLO QCD correction to ${Br(t\rightarrow qh)}$, which is calculated to be ${K_{\mathrm{QCD}}=1+0.97\alpha _{\mathrm{s}}\simeq 1.1}$ by the results of high order corrections to ${t\rightarrow wb}$ [68] and ${t\rightarrow qh}$[74,75,76].

Fig. 1

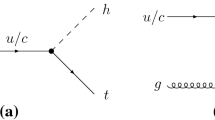
Illustrated Feynman diagrams for the processes ${e^{-} \mathrm{p} \rightarrow \nu _{\mathrm{e}} }\bar{{t}} \rightarrow \nu _{\mathrm{e}} h\bar{{q}} \rightarrow \nu _{\mathrm{e}} b\bar{{b}}\bar{{q}}$ (signal I) and ${e^{-} p \rightarrow \nu _{\mathrm{e}} hb \rightarrow \nu _{\mathrm{e}} b}\bar{{b}} {b}$ signal II) at the ep colliders that contain flavor changing top–Higgs interactions

3 Process analysis and numerical calculations

3.1 The signal and background analysis

Here we start to present our study on the anomalous tqh couplings at the ep colliders. Ep colliders are hybrids between the ${e^+e^-}$ and pp colliders, which consist of a hadron beam with an electron beam. They provide a cleaner environment compared with the pp colliders and higher center-of-mass (c.m.) energies compared with the ${e^+e^-}$ ones. Currently, the proposed ep collider is the Large Hadron Electron Collider (LHeC) [77,78,79,80], which is a combination of a 60 GeV electron beam and a 7 TeV proton beam of the LHC. It can deliver up to 100 ${ fb^{-1}}$ integrated luminosity per year at a c.m. energy of around 1 TeV and 1 ${ab^{-1}}$ over its lifetime. This may later be extended to the future circular electron–hadron collider (FCC-eh)[81], which features a 60 GeV (or maybe higher or maybe lower) electron beam with the 50 TeV proton beam from the future circular hadron–hadron collider (FCC-hh). This would result in a c.m. energy up to 3.5 TeV with comparable luminosities to the LHeC [82]. There is a lot of work, see for example, [83,84,85,86,87,88,89], that has been done in new physics searches, based on such proposed colliders, in order to try hard to enrich the physics motivations.

Fig. 2

Some examples of partonic Feynman diagrams for the reducible and irreducible backgrounds correspond to the signal

At the ep colliders, the first signal production which contains the top–Higgs FCNC couplings that we considered can be written as

$$\begin{aligned} \text {signal I: } \quad e^- p \rightarrow \nu _{\mathrm{e}} \bar{{t}} \mathrm {\rightarrow \nu _{\mathrm{e}} h }\bar{{q}} \rightarrow \nu _{\mathrm{e}} {b}\bar{{b}}\bar{{q}}, \end{aligned}$$

(6)

where q $=$ u or c, which is the largest channel compare to the other productions [65]. In this case, the five flavor scheme should be applied and an initial state bottom quark will collide with a w boson to produce a single top, which decays anomalously to a Higgs and a light quark. The Feynman diagram is plotted in Fig. 1 (left panel for signal I). As can be seen, the studied topology gives rise to the ${E^{\mathrm{miss}}_\mathrm{T} + jets}$ signature characterized by three or more than three) jets and a missing transverse momentum ${E^{\mathrm{miss}}_\mathrm{T}}$) from the undetected neutrino. Two of the jets should be tagged as B-jets. The combination of the two B-jets should appear as a narrow resonance centered around the SM Higgs boson mass. Together with the remaining light jets, one should be able to reconstruct a resonant top quark.

The second channel we considered is

$$\begin{aligned} \text {signal II: } \quad e^- p \rightarrow \nu _{\mathrm{e} h b \rightarrow \nu _{\mathrm{e}} b}\bar{{b}} \mathrm{b}. \end{aligned}$$

(7)

In this case, the FCNC tqh couplings are induced through light quarks that are directly emitted from the proton, which is different from signal I, where the tqh couplings are coming from the single top decays. At first glance, this contribution may not be small, because of the larger parton distribution functions (pdfs) of light quarks that hold inside the proton. However, its cross section is found to be much smaller than the first one, due to the suppression of the three-body phase space integration (before Higgs decay). There is another thing that may be interesting and worth to be noticed. Usually, the analysis of the ${ t\rightarrow ch}$ and ${t\rightarrow uh}$ final states have similar acceptances. This is true for our signal I, but not for signal II. For signal II, the charm quark pdfs are much more suppressed than that of the up quark, thus the analysis between ${t\rightarrow ch}$ and ${t\rightarrow uh}$ are quite different. In our analysis, we only concentrate on the ${t\rightarrow uh}$ mode as a reference throughout this work. Even for signal I, we should comment that if the ${t\rightarrow ch}$ mode is considered, the charm mis-tagging rate would also affect the signal acceptance. If so, one can use the technique based on studies in, for example, Ref. [90], in order to differentiate the ${ t\rightarrow ch}$ and ${t\rightarrow uh}$ decays. Considering the studied topology, we require that there should be three tagged B-jets for our signal II. This is indeed a critical selection, by applying which the backgrounds can be strongly suppressed, thus providing a much clean channel. This is the reason that signal II is also included in our study, though its production rate is small. Furthermore, we can find that in some cases the discovery potential through this channel can be even better than the former one. The related Feynman diagram is plotted in Fig. 1 (right panel for signal II). Both signal channels are belonging to the charge current productions at the ep colliders and their backgrounds are also quite similar, as which will be discussed in the following.

The main backgrounds come from both the reducible and irreducible ones. The crucial irreducible backgrounds which yield exactly the same final states to signal.I are listed bellow. See,

$$\begin{aligned}&{e^-p \rightarrow \nu _{\mathrm{e}} (h\rightarrow b }\bar{{b}} ) {j} \end{aligned}$$

(8)

$$\begin{aligned}&{e^-p \rightarrow \nu _{\mathrm{e}} (z\rightarrow b }\bar{{b}} ) {j} \end{aligned}$$

(9)

which contain three QED couplings, are noted as “bakh” and “bakz” respectively,

$$\begin{aligned}&{ e^-p \rightarrow \nu _{\mathrm{e}} (g\rightarrow b }\bar{{b}}) {j} \end{aligned}$$

(10)

which contains two QED couplings and two QCD couplings, is noted as “bakg”. Notice here and bellow, j = g, u, $\bar{u}$, d, $\bar{d}$, c, $\bar{c}$, s, $\bar{s}$. One source of the most important potentially reducible backgrounds is

$$\begin{aligned}&e^-p \rightarrow \nu _{\mathrm{e}} jjj \nonumber \\&e^-p \rightarrow \nu _{\mathrm{e}} jjb/\bar{b} \end{aligned}$$

(11)

due to a mis-identification of one or more of the final state light jets to B-jets. These processes contain two QED couplings and two QCD couplings as well. We refer them as “bakjjj” (including “bakg” backgrounds). Another source of reducible background is single top production. As can be seen, the signal process studied in our paper is essentially single top production at the ep collider, followed by a particular decay chain. This means that SM single top production and decay is an important background to our signal production under consideration. We refer these backgrounds as “bakt”. The production is

$$\begin{aligned}&e^-p \rightarrow \nu _{\mathrm{e}} (\bar{t} \rightarrow ( w^- \rightarrow jj) \bar{b} ). \end{aligned}$$

(12)

The produced top quark will decay to a w boson and a B-jet. The hadronic decay of the w boson to non-B-jets final states, which might mis-tagged as a B-jet, make this background a dangerous one. We have also looked into some neutral current (NC) production backgrounds:

$$\begin{aligned}&e^-p \rightarrow e^- jjj \nonumber \\&e^-p \rightarrow e^- jjb/\bar{b} \nonumber \\&e^-p \rightarrow e^- (g\rightarrow b\bar{b}) j. \end{aligned}$$

(13)

These are NC multi-jet backgrounds (“bakejjj”) and belong to reducible ones. Applying a no-lepton selection, they can be strongly reduced and safely ignored, thus they are not considered. To be clear, we present some Feynman diagrams for the backgrounds in Fig. 2. Typically, Fig. 2 (a), (b), (c), (d, e), (f) and (g, h) correspond to bakh, bakz, bakg, bakjjj, bakt and bakejjj respectively. All the backgrounds listed above are also belonging to the backgrounds of signal II, but all are the irreducible ones, due to a mis-identification of one or more of the final state light jets to B-jets.

3.2 The simulation

For the simulation of the collider phenomenology, we use FeynRules [91] to extract the Feynman rules from the Lagrangian. The model is generated into Universal FeynRules Output (UFO) files [92] and then fed to the Monte Carlo event generator MadGraph@NLO [93] for the generation of event samples. We pass the generated parton level events on to PYTHIA6.4 [94], which handles the initial and final state parton shower, hadronization, heavy hadron decays, etc. Then, we pass the events on to Delphes [95], which handles the detector effect. The detector is assumed to have a cylindrical geometry comprising a central tracker followed by an electromagnetic and a hadronic calorimeter. The forward and backward regions are also covered by a tracker, an electromagnetic calorimeter and a hadronic calorimeter. The angular acceptance for charged tracks in the pseudorapidity range $-4.3< \eta < 4.9$ and the detector performance, in terms of momentum and energy resolution of electrons, muons and jets, is based on the LHeC detector design [78, 80]. We use FASTJET [96] for jet clustering. Jets are anti-kt clustered [97] with a cone of radius $\Delta R j)=\sqrt{\Delta \eta ^2+\Delta \phi ^2}=0.7 0.4)$ at the LHeC (FCC-eh). The B-jet tagging technique is applied and the C (light)-quark mis-tagging rates as B-jets are included. We use NN23LO1 [98, 99] parton distribution functions for all event generations. The factorization and renormalization scales for both the signal and the background simulation are done with the default MadGraph5 dynamic scales. The electron polarization is assumed to be unit for the unpolarized case, and the results may increase by a factor of $1+P_\mathrm{e}$ if the polarized electron beam is considered, where $P_\mathrm{e}$ is the degree of the longitudinal polarization of the beam. Notice this is only true for CC productions at the ep colliders, while for NC production the results should be calculated correspondingly. We take $P_\mathrm{e} = 0.8$ as the default value. We take all the low flavored quarks, gluon and also the b-quark fluxes inside proton. In our numerical calculation, the SM inputs are $\alpha _{\mathrm{M}_\mathrm{Z}}=1/127.9$, $G_\mathrm{f}=1.1663787\times 10^{-5}\,\mathrm{GeV}^{-2}$, $\alpha _\mathrm{s}=0.1182$, $M_\mathrm{Z}=91.1876\,\mathrm{GeV}$, $M_\mathrm{w}=79.82\ \mathrm{GeV}$, $M_{\mathrm{top}}=173.2\ \mathrm{GeV}$ and $M_\mathrm{h}=125.09\,\mathrm{GeV}$. The typical fixed value of $\kappa _{\mathrm{tuh}}=0.1$ is chosen as the benchmark point if not stated otherwise. To estimate the event rate at parton level for the signal, we apply the following basic pre-selections:

$$\begin{aligned}&p_\mathrm{T}^{k_0} \ge 20\ \mathrm{GeV},\nonumber \\&|\eta ^{k_0}| < 10, \ \ k_0=j, b, \ell , \nonumber \\&\Delta R (k_1 k_2) >0.01, \ \ k_1 k_2=jj, j\ell , jb, bb, b\ell , \end{aligned}$$

(14)

where $\Delta R = \sqrt{\Delta \Phi ^2 + \Delta \eta ^2}$ is the separation in the rapidity ($\eta$–azimuth $\Phi$) plane, $p_\mathrm{T}^{\mathrm{j, b}, \ell }$ are the transverse momentum of jets, B-jets and leptons. The cuts are defined in the lab frame.

Fig. 3

The cross sections for signal I $e^- p \rightarrow \nu _{\mathrm{e}} \bar{t} \rightarrow \nu _{\mathrm{e}} h \bar{q}$ and signal II $e^- p \rightarrow \nu _{\mathrm{e}} h b$ as a function of the top–Higgs FCNC couplings $\kappa _{\mathrm{tqh}}$ at the 7 TeV LHeC and 50 TeV FCC-eh. The electron beam is 60 GeV

3.3 The cross sections and distributions

Before doing the full signal and background simulation, we present the cross section of the signals (without Higgs to $b\bar{b}$ decay) in order to provide a basic idea of its production rate. The proton beam energy is chosen to be 7–50 TeV and the electron beam is 60 GeV as proposed. We show the dependence of the cross sections $\sigma$ in units of fb as a function of $\kappa _{\mathrm{tqh}}$ for three different cases:

• (I) $\kappa _{\mathrm{tqh}}= \kappa _{\mathrm{tuh}}, \kappa _{\mathrm{tch}} =0$,

• (II) $\kappa _{\mathrm{tqh}}= \kappa _{\mathrm{tch}}, \kappa _{\mathrm{tuh}} =0$,

• (III) $\kappa _{\mathrm{tqh}}= \kappa _{\mathrm{tuh}} = \kappa _{\mathrm{tch}}$.

The results are plotted in Fig. 3. The first three figures present the cross sections for signal I and the last three for signal II. The lower two curves are the results at the LHeC and the upper two ones are at the FCC-eh. As shown in the figures, the production rate is enhanced obviously when $\kappa _{\mathrm{tqh}}$ is becoming larger. We can see that the cross section at the FCC-eh is around ten times larger than that at the LHeC. From the first two figures of signal I, we can see that the $t\rightarrow uh$ (case I) and $t\rightarrow ch$ (case II) final states have similar production rates. This is not the same for signal II, where the cross section in case II) is much smaller than that in case I), due to the small values of the charm quark pdfs.

Now let us study the signal and the backgrounds at the distribution level. After adopting the basic cuts in Eq. (14), our sample selection for signal I is simply

$$\begin{aligned} E^{\mathrm{miss}}_\mathrm{T}\ +\ 0\ \ell \ +\ \ge 3 \text { jets, } \ (\text {with 2 tagged B-jets}). \end{aligned}$$

(15)

Taking the typical benchmark input for the signal ($\kappa _{\mathrm{tuh}}=0.1$), the expected cross section before the selection is about 7.96 (64.24) fb at the LHeC (FCC-eh), and 1.05 (18.06) fb after it. In Fig. 4, we present some distributions, including the reconstruction of the top mass ($M_{\mathrm{top}}$) and the Higgs mass ($M_\mathrm{h}$), the transverse momentum distribution of the light jet ($p_\mathrm{T}^{\mathrm{light\,jet}}$), the top system ($p_\mathrm{T}^{\mathrm{top}}$) and the Higgs ($p_\mathrm{T}^{\mathrm{h}}$), the scalar sum of transverse momenta (HT), as well as the rapidity separation between the leading B-jet (one of which reconstructs the Higgs boson) and the light-jet $\Delta \eta ^{\mathrm{B}_{\mathrm{j}_1}\mathrm{L}_{\mathrm{j}_3}}$), and the rapidity–azimuth plane separation between the two B-jets that reconstruct the Higgs boson ($\Delta R^{\mathrm{B}_{\mathrm{j}_1}\mathrm{B}_{\mathrm{j}_3}}$). In order to reconstruct the top system, we use two methods. One is that we choose three jets randomly, find the three ones with their invariant mass close to the top mass ($M_{\mathrm{j}_{1}\mathrm{j}_{2}\mathrm{j}_{3}}$) and fill in the histogram. The second one is that we find the B-jets that reconstruct the Higgs boson first, and then find the light jet from the top system similarly ($M_{\mathrm{B}_{\mathrm{j}_1}\mathrm{B}_{\mathrm{j}_2}\mathrm{L}_{\mathrm{j}_{3}}}$). The solid red curve is for the signal production. We can find clear peaks around the Higgs mass and top mass, unfortunately, both for signal and backgrounds. The dashed blue curves, dotted black curves, short-dash-dotted violet curves and long-dash-dotted green ones are for bakt, bakh, bakz and bakjjj, respectively. All the plots are unit normalized. The results are for signal I at the 50 TeV $\oplus$ 60 GeV@FCC-eh, while for the results at the 7 TeV$\oplus$ 60 GeV@LHeC we can get similar ones, which are not shown.

Fig. 4

Various kinematical distributions for signal I and backgrounds at the FCCeh. The electron beam is 60 GeV. Here $\kappa _{\mathrm{tuh}}=0.1$. Plots are unit normalized

Fig. 5

Various kinematical distributions for signal II and backgrounds at the 50 TeV FCC-eh. The electron beam is 60 GeV. Here $\kappa _{\mathrm{tuh}}=0.1$. Plots are unit normalized

Table 1 Cross sections (in units of fb) and significance depending on the cut flows for signal I $\ e^- p \rightarrow \nu _{\mathrm{e}} \bar{t} \rightarrow \nu _{\mathrm{e}} h \bar{q} \rightarrow \nu _{\mathrm{e}} b\bar{b} \bar{q}$ ($\kappa _{tuh}=0.1$) and backgrounds at the 7 TeV $\oplus$ 60 GeV @LHeC and 50 TeV $\oplus$ 60 GeV @FCC-eh. ${\mathcal {SS}}$ is evaluated with $1\ ab^{-1}$ integrated luminosity. Polarization effects and systematic uncertainty are not considered yet

Table 2 Cross sections (in units of fb) and significance depending on the cut flows for signal II $\ e^- p \rightarrow \nu _{\mathrm{e}} h b \rightarrow \nu _{\mathrm{e}} b\bar{b} b$ ($\kappa _{\mathrm{tuh}}=0.1$) and backgrounds at the 7 TeV $\oplus$ 60 GeV @LHeC and 50 TeV $\oplus$ 60 GeV @FCC-eh. ${\mathcal {SS}}$ is evaluated with $1\ ab^{-1}$ integrated luminosity. Polarization effects and systematic uncertainty are not considered yet

The analysis is similar for signal II, where the selection is found directly to be

$$\begin{aligned} E^{\mathrm{miss}}_\mathrm{T}\ +\ 0\ \ell \ +\ \ge 3 \text { jets, } \ \text { (with 3 tagged B-jets)}. \end{aligned}$$

(16)

We choose the distributions which show good potential to separate the signal over backgrounds and plot them in Fig. 5. The first one is to reconstruct the top system using three random jets. We expect, and do find, a similar peak for the signal as for bakz and bakh backgrounds. However, there still seems to be overlap between the signal and bakt background. The second distribution is the invariant mass of the three B-jets system, instead of the top system. In this case, the signal and bakt background are no longer a peak but a bump, with some long tails especially for the signal. Choosing two of the B-jets, we can reconstruct the Higgs boson in the third distribution. The fourth and fifth ones are $\Delta \Phi ^{\mathrm{hB}_{\mathrm{j}_3}}$ and $p_\mathrm{T}^{\mathrm{B}_{\mathrm{j}_{2}}}$ distributions where $B_{\mathrm{j}_{1 2)}}$ is one of the B-jets that reconstruct the Higgs boson. The most interesting distribution is the last one, $p_\mathrm{T}^{\mathrm{B}_{\mathrm{j}_{3}}}$, the transverse momentum distributions for the B-jets not belonging to any of the B-jets that reconstruct the Higgs. There is a long tail for the signal in the large pt region, while for all the other backgrounds, there seems to be preference of a forward B-jet (or a forward jet faked as a B-jet), which drops quickly in the low pt regions.

Fig. 6

The upper limit on $Br t\rightarrow uh)$ at 99.99, 99.73, 95.40, 68.27$\%$ C.L. as a function of the integrated luminosity at the 7 (50) TeV LHeC (FCC-eh) with 60 GeV electron beam for signal I and signa.II. The dashed blue, black solid, dotted violet and dash-dotted red curves present 1$\sigma$, 2$\sigma$, 3$\sigma$ and 5$\sigma$ significance, respectively. $80\%$ polarization and $5\%$ systematic uncertainty for backgrounds yields only are taken into account

Table 3 Cross sections (in units of fb) and significance depending on the cut flows for signal I $\ e^- p \rightarrow \nu _{\mathrm{e}} \bar{t} \rightarrow \nu _{\mathrm{e}} h \bar{q} \rightarrow \nu _{\mathrm{e}} b\bar{b} \bar{q}$ ($\kappa _{\mathrm{tuh}}=0.1$) and backgrounds at the 7 TeV $\oplus$ 40 GeV @LHeC and 7 TeV $\oplus$ 50 GeV @FCC-eh. ${\mathcal {SS}}$ is evaluated with $1\ ab^{-1}$ integrated luminosity. Polarization effects and systematic uncertainty are not considered yet

Fig. 7

The left panel is the $2\sigma$ $\kappa _{\mathrm{tuh}}$ limit as a function of the luminosities. The solid black, dashed violet and dotted red curves are for the 60, 50 and 40 GeV LHeC. The right panel is the ratio defined as $\delta ^{\mathrm{E}} = \frac{Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{E}} - Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{60\,GeV}} }{Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{60\,GeV}}}$, where E is equal to 50 or 40 GeV

Table 4 Cross sections (in units of fb) and significance depending on the cut flows for signal I $\ e^- p \rightarrow \nu _{\mathrm{e}} \bar{t} \rightarrow \nu _{\mathrm{e}} h \bar{q} \rightarrow \nu _{\mathrm{e}} b\bar{b} \bar{q}$ ($\kappa _{\mathrm{tuh}}=0.1$) and backgrounds at the 50 TeV $\oplus$ 40 GeV @FCC-eh and 50 TeV $\oplus$ 50 GeV @FCC-eh. ${\mathcal {SS}}$ is evaluated with $100\ fb^{-1}$ integrated luminosity. Polarization effects and systematic uncertainty are not considered yet

3.4 The selections and discovery potential at the ep colliders

3.4.1 The comparison between the two signal channels

We choose the optimized selections depending on the behavior of the distributions. For signal I, the optimized cuts are the mass windows of $M_\mathrm{h}$, $M_{\mathrm{top}}$ $M_{\mathrm{j}_1 j_2 j_3}$), and the cuts on HT. The cross section and significance dependence on the cut flows are shown in Table 1. Notice that when the colliding energy is different, the order of the optimized selections (corresponding to the significance from small to large) and the values of cuts are not exactly the same. Which one is the best cut in each step and what the corresponding significance is, are questions that are determined in a somewhat automatic way, depending on the machine computation. Finally, we find that, with the integrated luminosity of 1$ab^{-1}$ at the 7 TeV $\oplus$ 60 GeV@LHeC 50 TeV $\oplus$ 60 GeV @FCC-eh), the significance is 5.9 (30.0) for signal I ($\kappa _{\mathrm{tuh}}=0.1$). Here the significance is calculated by the following formula:

$$\begin{aligned} {\mathcal {SS}} = \sqrt{2\left[ (n+b)\log \left( 1+\frac{n}{b}\right) -n\right] } \end{aligned}$$

(17)

where n is the number of events and b is the number of backgrounds evaluated with the corresponding integrated luminosity. We also find that among all the backgrounds, the bakt is indeed the most dangerous one, and it accounts for more than $70\%$ of the total backgrounds. The question of how to suppress the single top background efficiently at the ep collider would be interesting; Ref. [57] may give some ideas. We leave this to a deeper study in future work.

The optimized selections for signal II include $p_\mathrm{T}^{\mathrm{B}_{\mathrm{j}_{ (2,3)}}}$, $\Delta R^{\mathrm{hB}_{\mathrm{j}_{3}}}$ and mass windows of $M_\mathrm{h}$. The cut flow dependence is shown in Table 2. Compared with signal I, signal II has one clear advantage, say, the three tagged B-jets selection can reduce the backgrounds strongly. However, its small production rate indicates its disadvantage, only 0.64 (3.085) fb at the LHeC FCC-eh) after the basic sample selections. Considering $1\ ab^{-1}$ luminosity, the significance is calculated to be 4.02 (16.7), not small, showing good potential in the measurement of the anomalous tqh couplings. Actually, soon we may find its discovery potential is already comparable to (at the LHeC) or even better than (at the FCC-eh) signal I.

In Fig. 6, the upper limit on $Br t\rightarrow uh)$ at 99.99, 99.73, 95.40, 68.27$\%$ C.L. as a function of the integrated luminosity at the 7 (50) TeV LHeC (FCC-eh) with 60 GeV electron beam are plotted. The dashed blue, solid black, dotted violet and dash-dotted red curves present 1$\sigma$, 2$\sigma$, 3$\sigma$ and 5$\sigma$ significance, respectively. The first two figures are for signal I and the second two are for signal II. Our conclusion is that, for signal I, at the high luminosity (up to 1$ab^{-1}$) ep colliders where the electrons have a polarization of $80\%$ and the electron energy is typical 60 GeV, the 1$\sigma$, 2$\sigma$, 3$\sigma$ and 5$\sigma$ upper limits on $Br t\rightarrow uh)$ are $0.075\times 10^{-2}$ ($0.14\times 10^{-3}$), $0.15\times 10^{-2}$ ($0.29\times 10^{-3}$), $0.22\times 10^{-2}$ ($0.43\times 10^{-3}$) and $0.38\times 10^{-2}$ ($0.72\times 10^{-3}$) at the LHeC (FCC-eh). For signal II, the boundaries become $0.064\times 10^{-2}$ ($0.097\times 10^{-3}$), $0.15\times 10^{-2}$ ($0.22\times 10^{-3}$), $0.26\times 10^{-2}$ ($0.35\times 10^{-3}$) and $0.53\times 10^{-2}$ ($0.68\times 10^{-3}$) at the LHeC (FCC-eh), respectively. We can see that signal II can even have better potential than signal I at the FCC-eh due to its clean environment. Notice here we use $5\%$ systematic uncertainty for background yields only at both ep colliders.

3.4.2 The comparison with the other limits

Here we compare our discovery potential with the other studies. Some references present limit on $Br(t\rightarrow qh)$. For example, Ref. [63] probe the observability of the top-Higgs FCNC couplings through the process $e^-e^+\rightarrow t(\rightarrow \ell \nu \ell b)\bar{t}(\rightarrow qh)$. It is shown that the branching ratio can be probed down to $1.12\times 10^{-3}$ at $95\%$ C.L. at the center-of-mass energy of 500 GeV with the integrated luminosity of 3000 $fb^{-1}$. This limit can be further improved when the polarizations of both lepton beams are included [64]. Reference [59], present the study through the process $pp \rightarrow W^-(\rightarrow \ell ^- \bar{\nu }\ell )h(\rightarrow \gamma \gamma )j$, and show that the branching ratios $Br(t\rightarrow qh)$ can be probed to $0.16\%$ at $3\sigma$ level at 14 TeV LHC with an integrated luminosity of 3000 $fb^{-1}$. Through some other channels, this limit can actually be pushed to even lower values. As proposed in [100], at the High-luminosity(HL)-LHC, the $95\%$ CL upper limit $Br(t\rightarrow qh)$ can be estimated up to the order of $2\sim 5\times 10^{-4}$ by a scaling with the luminosity, based on the studies in Ref. [54].

Some references present the limits on $Br(t\rightarrow uh)$, which we can easily compare with. As shown in Ref. [56], through $t\bar{t}\rightarrow W^{+}b + qh \rightarrow \ell ^+\nu b + \gamma \gamma q$ channel at the LHC, the branching ratios $Br(t\rightarrow uh)$ can be respectively probed to $0.23\%$ at $3\sigma$ level at 14 TeV LHC with $L=3000\ fb^{-1}$. This limits can be improved in Ref. [57] where the authors apply a development version of HEPTopTagger algorithm. They found that, through multilepton searches ($th\rightarrow \ell ^+\nu b+\ell ^+\ell ^- X$), vector boson plus Higgs search ($th\rightarrow \ell ^+\nu b + \tau ^+\tau ^-$) and fully hadronic search ($th\rightarrow jjb+b\bar{b}$), the limits are found to be $0.22\%$, $0.15\%$ and $0.36\%$ by using $100\ fb^{-1}$ of 13 TeV data.

Concerning our results, with $80\%$ electron polarization, 1$ab^{-1}$ integrated luminosity, and $5\%$ system uncertainty from background yields only, the $3\sigma$ limits are $0.22\times 10^{-2}$ at the 7 TeV $\oplus$ 60 GeV @LHeC and $3.5\times 10^{-4}$ at the 50 TeV $\oplus$ 60 GeV @FCC-eh. Comparing the limits we obtained with the others, on one hand, our limits are better than the limits from the 8 TeV 20.3 19.7) $fb^{-1}$ data at the ATLAS CMS, say, $Br t\rightarrow uh) \le 4.5 5.5)\times 10^{-3}$ [42]; on the other hand, comparable to or even better than some phenomenological studies at the other colliders. In such a case the ep colliders may play an important role of double checks if the anomalous tqh couplings are really discovered at the LHC or (HL)-LHC.

Fig. 8

The left panel is the $2\sigma$ $\kappa _{\mathrm{tuh}}$ limit as a function of the luminosities. The solid black, dashed violet and dotted red curves are for the 60, 50 and 40 GeV FCC-eh. The right panel is the ratio defined as $\delta ^{\mathrm{E}} = \frac{Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{E}} - Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{60\,GeV}} }{Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{60\,GeV}}}$, where E is equal to 50 or 40 GeV

3.4.3 The sensitivity dependence on the electron beam energy change

In the above analysis we explore the potentials at the high luminosity up to 1 $ab^{-1}$) ep colliders where the electrons have a polarization of $80\%$. The electron energy is typical 60 GeV, but lower energies are interesting due to the cost. Therefore, we give an estimate of how our sensitivity (taking signal I as an example) would change when we reduce the electron beam energy from 60 to 50 GeV or even 40 GeV. In Table 3 we present the results at the 40 and 50 GeV LHeC. Compared with the 60 GeV LHeC, the significance is reduced from 5.9 to 5.37 (4.52) for 50 (40) GeV.

A more straightforward comparison is presented in Fig. 7. The left panel is the $2\sigma$ $Br t\rightarrow uh)$ limit as a function of the luminosities. The solid black, dashed violet and dotted red curves are for the results of 60, 50 and 40 GeV at the LHeC. In the right panel, we define the ratio

$$\begin{aligned} \delta ^{\mathrm{E}} = \frac{Br^{\mathrm{E}}_{\mathrm{t}\rightarrow \mathrm{uh}} - Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{60\,GeV}} }{Br_{\mathrm{t}\rightarrow \mathrm{uh}}^{\mathrm{60\,GeV}}}, \end{aligned}$$

(18)

where E equals 50 or 40 GeV. The dashed violet curve is for $\delta ^{\mathrm{50\,GeV}}$ and the dotted red one is for $\delta ^{\mathrm{40 \,GeV}}$. We see that when the energy of electron beam is reduced from 60 to 50 (40) GeV, the discovery potential is reduced around 8.7 (29.4)%. We also check that these numbers will not change no matter if we are using the 1$\sigma$, 2$\sigma$, 3$\sigma$ or 5$\sigma$ limits. So we conclude that the discovery potential is reduced $8.7\%$ ($29.4\%$) if the electron beam changes from 60 to 50 (40) GeV at the 7 TeV LHeC.

The same comparison is done in Table 4 for the 40 and 50 GeV FCC-eh. Compared with the 60 GeV FCC-eh, the significance is reduced from 30.0 to 25.8 (25.1) for 50 (40) GeV FCC-eh with 1 $ab^{-1}$). A similar ratio is plotted in Fig. 8. It is found that when the energy of electron beam is reduced from 60 to 50 (40) GeV, the discovery potential is reduced about 16.8 (19.8)% correspondingly.

4 Conclusion

In this paper we present an updated analysis on searches for the anomalous flavor changing neutral current (FCNC) Yukawa interactions between the top quark, the Higgs boson, and either an up or charm quark ($tqh, q=u, c$). We probe the observability of the FCNC top–Higgs couplings through the process $e^- p\rightarrow \nu _{\mathrm{e}} \bar{t} \rightarrow \nu _{\mathrm{e}} h \bar{q}$ (signal I) and $\ e^- p \rightarrow \nu _{\mathrm{e}} h b$ (signal II) at the ep colliders where the Higgs boson decays to a $b\bar{b}$ pair. We perform the results from the cut-and-count based method. Our results show that with $80\%$ electron polarization, 1 $ab^{-1}$ integrated luminosity, and $5\%$ system uncertainty from background yields only, the $3\sigma$ limits are $0.22\times 10^{-2}$ at the 7 TeV $\oplus$ 60 GeV @LHeC and $3.5\times 10^{-4}$ at the 50 TeV $\oplus$ 60 GeV @FCC-eh. These limits are, on one hand, better than the current limits for the experiments; on the other hand, comparable to or even better than some phenomenological studies at the other colliders. We also give an estimate of how our sensitivity (taking signal I as an example) would change when we reduce the electron beam energy from 60 to 50 GeV or even 40 GeV due to the cost. The conclusion is that the discovery potential is reduced to $8.7\%$ ($29.4\%$) if the electron beam changes from 60 to 50 (40) GeV at the 7 TeV LHeC, and $16.8\%$ ($19.8\%$) at the 50 TeV FCC-eh. In summary, we give a detailed overview on the search potential for the anomalous top–Higgs couplings at the ep colliders including the LHeC as well as the FCC-eh.