$\mu \rightarrow e \gamma$ and matching at $\varvec{m_W}$

Abstract

Several experiments search for $\mu \leftrightarrow e$ flavour change, for instance in $\mu \rightarrow e ~\mathrm{conversion}$, $\mu \rightarrow e \gamma$ and $\mu \rightarrow e \bar{e} e$. This paper studies how to translate these experimental constraints from low energy to a New Physics scale $M \gg m_W$. A basis of QCD $\times$ QED-invariant operators (as appropriate below $m_W$) is reviewed, then run to $m_W$ with one-loop Renormalisation Group Equations (RGEs) of QCD and QED. At $m_W$, these operators are matched onto SU(2)-invariant dimension-six operators, which can continue to run up with electroweak RGEs. As an example, the $\mu \rightarrow e \gamma$ bound is translated to the scale M, where it constrains two sums of operators. The constraints differ from those obtained in previous EFT analyses of $\mu \rightarrow e \gamma$, but they reproduce the expected bounds on flavour-changing interactions of the Z and the Higgs, because the matching at $m_W$ is pragmatically performed to the loop order required to get the “leading” contribution.

1 Introduction

Neutrino masses and mixing angles imply that “New” Physics from beyond the Standard Model(SM) must be present in the lepton sector, and must induce charged Lepton Flavour Violation (LFV; for a review, see [1]). However, neither LFV nor the origin of neutrino masses has yet been discovered. This study assumes that the required new particles are heavy, with masses at or beyond $M > m_W$. In addition, between $m_W$ and M, there should be no other new particles or interactions which affect the LFV sector. One approach to identifying this New LFV Physics, is to construct a motivated model, and identify its signature in observables [2–30]. A more pragmatic approach, which requires optimism but no model-building skills, is to parametrise the New Physics at low energy with non-renormalisable operators, map the experimental constraints onto the operator coefficients, and attempt to reconstruct the fundamental Lagrangian of New Physics from the operator coefficients. This is probably not feasible, but could give interesting perspectives. A first step in this “bottom-up” approach, explored in this paper, is to use Effective Field Theory (EFT) [31] to translate the experimental bounds to the coefficients of effective operators at the New Physics scale $M> m_W$.

The goal would be to start from experimental constraints on $\mu$–e flavour change, and obtain at M the best bound on each coefficient from each observable. These constraints should be of the correct order of magnitude, but not precise beyond one significant figure. This preliminary study restricts the experimental input to the bound on $BR(\mu \rightarrow e \gamma )$, and makes several simplifications in the translation up to the New Physics scale M. Firstly, the EFT has three scales: a low scale $m_\mu \sim m_b$, the intermediate weak scale $m_W$, and the high scale M. Secondly, at a given scale, the EFT contains lighter Standard Model particles and dimension-six, gauge-invariant operators (one dimension-seven operator is listed; however, dimension-eight operators are neglected). The final simplification might have been to match at tree level, and run with one-loop Renormalisation Group Equations (RGEs). However, a bottom-up EFT should reproduce the results of top-down model calculations, and it is straightforward to check that one- and two-loop matching is required at $m_W$ to obtain the correct bounds from $\mu \rightarrow e \gamma$ on LFV interactions of the Z and Higgs. So the matching at $m_W$ is performed to the order required to get the known bounds.

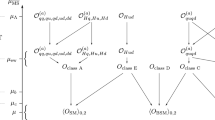
The paper is organised in two parts: the Sects. 2–4 construct some of the framework required to obtain experimental constraints on SU(2)-invariant operator coefficients at $m_W$, then Sect. 5 focusses on using, checking and improving this formalism to obtain bounds from $\mu \rightarrow e \gamma$ on operator coefficients at M. The formalism can be organised in four steps: matching at $m_\mu$, running to $m_W$, matching at $m_W$, then running up to the New Physics scale M. Section 2 reviews the basis of QCD$\times$QED-invariant operators, as appropriate below $m_W$. These operators, of dimension five, six and seven, describe three- and four-point functions involving a $\mu$, an e and any other combination of flavour-diagonal light particles. To complete the first step, the experimental bounds should be matched onto these operator coefficients; however, this is delayed till Sect. 5, where only the bound on $\mu \rightarrow e \gamma$ is imposed on the dipole coefficients (the bounds from $\mu \rightarrow e ~\mathrm{conversion}$ and $\mu \rightarrow e \bar{e} e$ are neglected for simplicity; the strong interaction subtleties of matching to $\mu \rightarrow e ~\mathrm{conversion}$ are discussed in [33–36]). Section 3 discusses the second step, which is to run the coefficients up to $m_W$ with the RGEs of QED and QCD. Appendix B gives the anomalous dimension matrix mixing the scalar and tensor operators to the dipole (which is responsable for $\mu \rightarrow e \gamma$). The anomalous dimension matrix for vector operators is neglected for two reasons: although vectors contribute at tree level to $\mu \rightarrow e ~\mathrm{conversion}$ and $\mu \rightarrow e \bar{e} e$, these experimental bounds are not included, and the leading order mixing of vectors to the dipole is at two-loop in QED, whereas the running here is only performed at one-loop. The next step is to match these operators at $m_W$ onto the Buchmuller–Wyler [37] basis of SU(2)-invariant operators as pruned in [38], which is referred to as the BWP basis. The tree-level matching for all operators is given in Sect. 4; if this is the leading contribution to the coefficients, then imposing SU(2) invariance above $m_W$ predicts some ratios of coefficients below $m_W$, as discussed in Sect. 4.2. Section 5 uses the formalism of the previous sections to translates the experimental bound on $BR(\mu \rightarrow e \gamma )$ to sums of SU(2)-invariant operator coefficients at $m_W$. Then a few finite-loop contributions are added, and the coefficients are run up to M, using a simplified version of the one-loop QCD and electroweak RGEs [39, 40, 43]. Finally, Sect. 6 discusses various questions arising from this study, such as the loop order required in matching at $m_W$, whether the non-SU(2)-invariant basis is required below $m_W$, and the importance of QED running below $m_W$.

Many parts or this analysis can be found in previous literature. Czarnecki and Jankowski [41] emphasized the one-loop QED running of the dipole operator (neglected in the estimates here), which shrinks the coefficient at low energy. Degrassi and Giudice [42] give the leading order QED mixing of vector operators to the dipole, which is also neglected here, because it arises at two loop. In an early top-down analysis, Brignole and Rossi [15] calculated a wide variety of LFV processes as a function of operator coefficients above $m_W$, without explicit Renormalisation Group running and a slightly redundant basis. Pruna and Signer [43] studied $\mu \rightarrow e \gamma$ in EFT, focussing on the electroweak running above $m_W$, which they perform in more detail than is done here. However, they do not obtain the bounds on the LFV couplings of the Z and Higgs that arise here in matching at $m_W$. Various one-loop contributions to $\mu \rightarrow e \gamma$ were calculated in [44], without organising them into running and matching parts. Finally, the contribution of the LFV Higgs operator to LFV Z couplings was beautifully studied in [45]. There are also many closely related works in the quark sector, reviewed in [46, 47]. For instance, the QED anomalous dimension matrix for various vector four-quark operators is given in [48], and matching at $m_W$ of flavour-changing quark operators is discussed in [49]. However, colour makes the quarks different, so it is not always immediate to translate the quark results to leptons.

2 A basis of $\mu$–e interactions at low energy

2.1 Interactions probed in muon experiments

Experiments searching for lepton-flavour change from $\mu$ to e, probe three- and four-point functions involving a muon, an electron and one or two other SM particles. I focus here on interactions that can be probed in $\mu \rightarrow e \gamma$, $\mu \rightarrow e \bar{e} e$ and $\mu \rightarrow e ~\mathrm{conversion}$, meaning that the interactions are otherwise flavour diagonal, and there is only one muon (so $K\rightarrow \bar{\mu }e$ and other meson decays is not considered).

These “new physics” interactions can be written as non-renormalisable operators involving a single $\mu$, and some combination of $e,\gamma ,g, u,d,$ or s. The operators should be QED and QCD invariant (because we are intested in LFV, not departures from the SM-gauge symmetries), and can be of any dimension (because the aim is to list the three-point and four-point interactions that the data constrains). The list, which can be found in [1, 33–35] but with different names, is:

$$\begin{aligned}&\mathrm{dipole} \quad \mathcal{O}^{e\mu }_{D,Y } = {m_\mu } (\overline{e} \sigma ^{\alpha \beta }P_Y \mu ) F_{\alpha \beta }\nonumber \\&\mathrm{4~lepton}\quad \mathcal{O}^{e\mu ee}_{YY} = \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{e} \gamma ^\alpha P_Y e ),\nonumber \\&\quad \quad \quad \quad \quad \mathcal{O}^{e\mu ee}_{YX} = \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{e} \gamma ^\alpha P_X e ),\nonumber \\&\quad \quad \quad \quad \quad \mathcal{O}^{e\mu ee}_{S,YY} = (\overline{e} P_Y \mu ) (\overline{e} P_Y e )\nonumber \\ \end{aligned}$$

$$\begin{aligned} \mathrm{2~lepton~2~quark} \quad \mathcal{O}^{e\mu uu}_{YY}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{u} \gamma ^\alpha P_Y u ),\nonumber \\ \mathcal{O}^{e\mu uu}_{YX}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{u} \gamma ^\alpha P_X u ),\nonumber \\ \mathcal{O}^{e\mu uu}_{S,YY}= & {} (\overline{e} P_Y \mu ) (\overline{u} P_Y u ),\nonumber \\ \mathcal{O}^{e\mu uu}_{S,YX}= & {} (\overline{e} P_Y \mu ) (\overline{u} P_X u ),\nonumber \\ \mathcal{O}^{e\mu uu}_{T,YY}= & {} (\overline{e} \sigma P_Y \mu ) (\overline{u} \sigma P_Y u ) \nonumber \\ \mathcal{O}^{e\mu dd}_{YY}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{d} \gamma ^\alpha P_Y d ) \nonumber \\ \mathcal{O}^{e\mu dd}_{YX}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{d} \gamma ^\alpha P_X d ), \nonumber \\ \mathcal{O}^{e\mu dd}_{S,YY}= & {} (\overline{e} P_Y \mu ) (\overline{d} P_Y d )\nonumber \\ \mathcal{O}^{e\mu dd}_{S,YX}= & {} (\overline{e} P_Y \mu ) (\overline{d} P_X d ), \nonumber \end{aligned}$$

$$\begin{aligned} \mathcal{O}^{e\mu dd}_{T,YY}= & {} (\overline{e} \sigma P_Y \mu ) (\overline{d} \sigma P_Y d ),\nonumber \\ \mathcal{O}^{e\mu ss}_{YY}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{s} \gamma ^\alpha P_Y s )\nonumber \\ \mathcal{O}^{e\mu ss}_{YX}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{s} \gamma ^\alpha P_X s ),\nonumber \\ \mathcal{O}^{e\mu ss}_{S,YY}= & {} (\overline{e} P_Y \mu ) (\overline{s} P_Y s ) \nonumber \\ \mathcal{O}^{e\mu ss}_{S,YX}= & {} (\overline{e} P_Y \mu ) (\overline{s} P_X s ),\nonumber \\ \mathcal{O}^{e\mu ss}_{T,YY}= & {} (\overline{e} \sigma P_Y \mu ) (\overline{s} \sigma P_Y s ) \nonumber \\ \mathrm{2~lepton~2~boson} \quad \mathcal{O}^{e\mu }_{GG,Y}= & {} \frac{1}{M}(\overline{e} P_Y \mu ) G_{\alpha \beta } G^{\alpha \beta }, \nonumber \\ \mathcal{O}^{e\mu }_{G\tilde{G},Y}= & {} \frac{1}{M} (\overline{e} P_Y \mu ) G_{\alpha \beta } \widetilde{G}^{\alpha \beta } \end{aligned}$$

(1)

where $X,Y \in \{L,R\}$, and $X\ne Y$. These operators are chosen, using Fierz and other spinor identities, to always have the lepton flavour-change inside a spinor contraction. Notice also that, following Kuno and Okada [1], the dipole is normalised with a muon Yukawa coupling. The four-fermion operators are labelled with the fermion flavours in superscript, and in the subscript is the type of Lorentz contraction (scalar, tensor or vector – except the vector case is implicit), followed by the chiralities of the two fermion contractions in subscript. The Lorentz contraction – dipole, scalar, tensor or vector – will be used throughout this paper to categorise operators. The operator coefficients have the same index structure, so $C^{ijkl}_{XX}$ is the coefficient of $\mathcal{O}^{ijkl}_{XX}$, which is a vector contraction of fermions of chirality X.

All the operators appear in the Lagrangian with a coefficient $-C/M^2$, and the operator normalisation is chosen to ensure that the Feynman rule is $-i C/M^2$. This implies a judicious distribution of $\frac{1}{2}$s, which is discussed in Appendix B.

Obtaining constraints from data on the operator coefficients is reviewed in [1], and $\mu \rightarrow e ~\mathrm{conversion}$ is discussed in [33–35]. Searches for $\mu \rightarrow e \gamma$ probe the dipole operator, $\mu \rightarrow e \bar{e} e$ probes the four-lepton operators and the (off-shell) dipole, and $\mu \rightarrow e ~\mathrm{conversion}$ probes the two-quark–two-lepton, diboson and dipole operators. It is interesting that these three processes are sensitive to almost all the three-and four-point functions that involve one muon, any of the lighter fermions, or photons or gluons. The only three- or four-point interactions not probed at tree level are the two-photon interactions,

$$\begin{aligned} \mathcal{O}^{e\mu }_{FF,Y} = (\overline{e} P_Y \mu ) F_{\alpha \beta } F^{\alpha \beta } ,\quad \mathcal{O}^{e\mu }_{F\tilde{F},Y} = (\overline{e} P_Y \mu ) F_{\alpha \beta } \widetilde{F}^{\alpha \beta }. \end{aligned}$$

2.2 Including heavy fermions

At a slightly higher scale, operators containing c, b $\mu$ and $\tau$ bilinears should be included. These additional operators are:

$$\begin{aligned} \mathrm{4~lepton} \quad \mathcal{O}^{e\mu ll}_{YY}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{l} \gamma ^\alpha P_Y l ),\nonumber \\ \mathcal{O}^{e\mu ll}_{YX}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{l} \gamma ^\alpha P_X l ), \nonumber \\ \mathcal{O}^{e\mu ll}_{S,YY}= & {} (\overline{e} P_Y \mu ) (\overline{l} P_Y l ),\nonumber \\ \mathcal{O}^{e\mu \tau \tau }_{S,YX}= & {} (\overline{e} P_Y \mu ) (\overline{\tau } P_X \tau ), \nonumber \\ \mathcal{O}^{e\mu \tau \tau }_{T,YY}= & {} (\overline{e} \sigma P_Y \mu ) (\overline{\tau } \sigma P_Y \tau ),\nonumber \\ \mathrm{2~lepton~2~quark} \quad \mathcal{O}^{e\mu qq}_{YY}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{q} \gamma ^\alpha P_Y q),\nonumber \\ \mathcal{O}^{e\mu qq}_{YX}= & {} \frac{1}{2}(\overline{e} \gamma ^\alpha P_Y \mu ) (\overline{q} \gamma ^\alpha P_X q ),\nonumber \\ \mathcal{O}^{e\mu qq}_{S,YY}= & {} (\overline{e} P_Y \mu ) (\overline{q} P_Y q),\nonumber \\ \mathcal{O}^{e\mu qq}_{S,YX}= & {} (\overline{e} P_Y \mu ) (\overline{q} P_X q ),\nonumber \\ \mathcal{O}^{e\mu qq}_{T,YY}= & {} (\overline{e} \sigma P_Y \mu ) (\overline{q} \sigma P_Y q ), \end{aligned}$$

(2)

where $l \in \{\mu ,\tau \}$, $q \in \{c,b\}$, $X,Y \in \{L,R\}$, and $X\ne Y$.

Including these operators introduces a second “low” scale into the EFT, which in principle changes the running and requires matching at this second low scale $m_\tau$. The running is discussed in the next section. Since the matching is at tree level, the operators present below $m_\tau$ have the same coefficient just above $m_\tau$. Were the dipole to be matched at one loop, then at $m_\tau$, one should compute the finite part of the diagrams [44] obtained by closing the heavy fermion loop of the tensors $\mathcal{O}^{e\mu bb}_{T,YY}$, $\mathcal{O}^{e\mu cc}_{T,YY}$ and $\mathcal{O}^{e\mu \tau \tau }_{T,YY}$, and attaching a photon (and also there could be similar finite contributions from four-fermion operators at $m_\mu$). Also, scalar operators involving b, c quarks would match at one loop onto $\mathcal{O}^{GG,Y}$ [50], as outlined in [51].

3 Running up to $m_W$

The operators of Eqs. (1) and (2) can evolve with scale due to QED and QCD interactions. QCD effects can be significant, and should be resummed, but fortunately they only change the magnitude of operator coefficients, without mixing one operator into another. This will be taken into account by multiplying two-lepton–two-quark operators by an appropriate factor (following Cirigliano et al. [35]). The effects of QED running are usually small, of order $\alpha _{em}/\pi$, but interesting because they give operator mixing. Therefore the QED renormalisation of individual operator coefficients is neglected, and only the mixing is included.

The scale at which the operators of Eqs. (1) and (2) start running is variable. The lepton operators of Eq. (1) will start their QED running at $m_\mu$, whereas those of Eq. (2) start at $m_\tau$. The the two-lepton-two-b operators start running up at $m_b$. For simplicity, the remaining two-quark–two-lepton operators are taken to start running up at $m_\tau$; that is, the experimental bounds are assumed to apply at a scale $\sim m_\tau$.

3.1 Defining the anomalous dimension matrix

After including one-loop corrections in $\overline{MS}$, the operator coefficients will run with scale $\mu$ according to

$$\begin{aligned} \mu \frac{\partial }{\partial \mu } \vec {C} = \frac{\alpha _{s}}{4\pi }\vec {C} {\varvec{\Gamma }}^{s} + \frac{\alpha _{em}}{4\pi }\vec {C} {\varvec{\Gamma }} \end{aligned}$$

(3)

where the coefficients of all the operators listed in the previous section have been organised into a row vector $\vec {C}$, and $\frac{\alpha _{em}}{4\pi } {\varvec{\Gamma }}$ is the anomalous dimension matrix, which is calculated as discussed in [47].¹

Equation (3) can be approximately solved, by neglecting the scale dependence of $\alpha _{em}$ and defining the eigenvalues of the diagonal ${\varvec{\Gamma }}^s$ to be $\{\gamma ^s_A\}$, as

$$\begin{aligned}&C_A(m_W)\left[ \frac{ \alpha _s(m_W)}{\alpha _s(m_\tau )}\right] ^{-\frac{\gamma ^s_A}{2 \beta _0}}\left( \delta _{AB} - \frac{\alpha _{em} }{4\pi } \left[ \Gamma \right] _{AB} \log \frac{m_W}{m_\tau } \right. \nonumber \\&\quad \left. + \frac{\alpha _{em} ^2 }{32\pi ^2} \left[ \Gamma \Gamma \right] _{AB} \log ^2 \frac{m_W}{m_\tau } +\cdots \right) = C_B (m_\tau ) \end{aligned}$$

(4)

where $\beta _0 = 11- 2N_f/3$ from the QCD $\beta$-function, and $\log \frac{m_W}{m_\tau } \simeq 3.85$.

It is convenient to separate the vector of coefficients below $m_W$, $\vec {C}(<m_W)$, into subvectors:

$$\begin{aligned} \vec {C}(<m_W)= & {} \Big (\vec {C}^{q_i}_V, \vec {C}^{u}_V, \vec {C}^{d}_V, \vec {C}^{\tau }_V, \vec {C}^{\mu }_V, \vec {C}^{e}_V, \nonumber \\&\vec {C}^{q_i}_S, \vec {C}^{u}_S, \vec {C}^{d}_S, \vec {C}^{\tau }_S, \vec {C}^{\mu }_{S \mu }, \nonumber \\&\vec {C}^{e}_{S e}, \vec {C}^{q_i}_T, \vec {C}^{u}_T, \vec {C}^{d}_T, \vec {C}^{\tau }_T, \vec {C}_D, \vec {C}_{GG}\Big ), \end{aligned}$$

(5)

$$\begin{aligned} \vec {C}_V^{ f}= & {} \left( C_{LL}^{e \mu f f}, C_{RR}^{e \mu f f}, C_{LR}^{e \mu f f}, C_{RL}^{e \mu f f}\right) , \end{aligned}$$

(6)

$$\begin{aligned} \vec {C}_S^{f}= & {} \left( C_{S,LL}^{e \mu f f}, C_{S,RR}^{e \mu f f}, C_{S,LR}^{e \mu f f}, C_{S,RL}^{e \mu f f}\right) \nonumber \\&\mathrm{for}~ f \in \{ q_i,u,d,\tau \}, \end{aligned}$$

(7)

$$\begin{aligned} \vec {C}_{Sl}^l= & {} \left( C_{S,LL}^{e \mu ll}, C_{S,RR}^{e \mu ll}\right) \quad \mathrm{for}~ l \in \{ e,\mu \}, \end{aligned}$$

(8)

$$\begin{aligned} \vec {C}_T^{f}= & {} \left( C_{T,LL}^{e \mu ff}, C_{T,RR}^{e \mu ff}\right) \end{aligned}$$

(9)

$$\begin{aligned} \vec {C}_D= & {} \left( C^{e \mu } _{D,L}, C^{e \mu } _{D,R}\right) , \end{aligned}$$

(10)

$$\begin{aligned} \vec {C}_{GG}= & {} \left( C^{e \mu }_{GG,L}, C^{e \mu }_{GG,R}\right) . \end{aligned}$$

(11)

QCD running concerns the two-lepton–two-quark operators, and the two-lepton-two-gluon operators. The gluon operators are neglected here, because they do not contribute at LO to $\mu \rightarrow e \gamma$, which is the example considered in Sect. 5, and because one-loop matching (not performed here) seems indicated in order to correctly account for these operators. The vector two-quark–two-lepton operators do not renormalise under QCD, because the quark vector currents are conserved: that is, diagram 4 of Fig.  1, with $f_2$ a quark and the photon replaced by a gluon, cancels against the wave-function renormalisation. However, the same diagram, plus wave-function renormalisation, causes the scalar operators to run like masses in QCD ($\gamma ^s = 6C_F$):

$$\begin{aligned} C_{S,XY}^{e \mu qq} (m_W)= & {} C_{S,XY}^{e \mu qq} (m_q) \left[ \frac{ \alpha _s(m_W)}{\alpha _s(m_q)}\right] ^{\frac{4}{\beta _0}} \nonumber \\&= C_{S,XY}^{e \mu qq} (m_q) \frac{m_q(m_W)}{m_q(m_q)} \end{aligned}$$

(12)

for $q \in \{u,d,s,c,b\}$ and $X,Y \in \{L,R\}$, so I follow [35] in normalising the coefficients with running quark masses as after the last equality. However, for the light quarks (u, d, s), the QCD running is stopped at $\mu \simeq m_\tau$, that is, $\alpha _s(m_q)$ is replaced by $\alpha _s(m_\tau )$. Finally, diagram 4 vanishes for the tensor four-fermion operators, but the wave-function diagrams cause the tensor operators to run as

$$\begin{aligned} C_{T,XY}^{e \mu qq} (m_W) = C_{T,XY}^{e \mu qq} (m_\tau ) \left[ \frac{ \alpha _s(m_W)}{\alpha _s(m_\tau )}\right] ^{\frac{-4/3}{\beta _0}}. \end{aligned}$$

(13)

Fig. 1

Examples of one-loop gauge vertex corrections to four-fermion operators. The first two diagrams are the penguins. The last six diagrams contribute to operator mixing and running, but can only change the Lorentz or gauge structure of the operators, not the flavour structure. Missing are the wave-function renormalisation diagrams; for $V \pm A$ Lorentz structure in the grey blob, this cancels diagrams 3 and 4

In QED running, the vector operators mix among themselves, but they have no mixing into or from the scalars and tensors. The scalars renormalise themselves and mix to tensors and in some cases to the dipoles, and the tensors renormalise themselves and mix to scalars and dipoles (which are dimension five, so they do not mix to other operators). So the anomalous dimension matrix can be written

$$\begin{aligned} {\varvec{\Gamma }}= \left[ \begin{array}{cc} {\varvec{\Gamma }}_V &{} 0\\ 0 &{} {\varvec{\Gamma }}_{STD} \end{array} \right] \end{aligned}$$

(14)

with

$$\begin{aligned} {\varvec{\Gamma }}_{STD}= \left[ \begin{array}{cccccccccccc} \gamma _{S,S}^{q_i,q_j} &{}0 &{}0 &{}0 &{}0 &{}0 &{}\gamma _{S,T}^{q_i,q_j} &{}0 &{}0 &{}0 &{}0 &{}0\\ 0&{}\gamma _{S,S}^{u,u} &{}0 &{}0 &{}0 &{}0 &{}0 &{}\gamma _{S,T}^{u,u} &{}0 &{}0 &{}0&{}0 \\ 0 &{}0 &{}\gamma _{S,S}^{d,d} &{}0 &{}0 &{}0 &{}0&{}0 &{}\gamma _{S,T}^{d,d} &{}0 &{}0&{}0 \\ 0&{}0 &{}0 &{}\gamma _{S,S}^{\tau ,\tau } &{}0 &{}0 &{}0 &{}0&{}0 &{}\gamma _{S,T}^{\tau ,\tau } &{}0&{}0 \\ 0&{}0 &{}0 &{}0 &{}\gamma _{S,S}^{\mu ,\mu } &{}0 &{}0 &{}0 &{}0 &{}0 &{}\gamma _{S,D}^{\mu ,} &{}0\\ 0 &{}0 &{}0 &{}0 &{}0 &{}\gamma _{S,S}^{e,e} &{}0 &{}0 &{}0 &{}0 &{} \gamma _{S,D}^{e,}&{}0\\ \gamma _{T,S}^{q_i,q_i} &{}0 &{}0 &{}0 &{}0 &{}0 &{}\gamma _{T,T}^{q_i,q_i} &{}0 &{}0 &{}0 &{}\gamma _{T,D}^{q_i,~} &{}0\\ 0 &{}\gamma _{T,S}^{u,u} &{}0 &{}0&{}0 &{}0 &{}0 &{}\gamma _{T,T}^{u,u} &{}0 &{}0 &{}\gamma _{T,D}^{u,~} &{}0\\ 0 &{}0 &{}\gamma _{T,S}^{d,d} &{}0&{}0 &{}0 &{}0 &{}0 &{}\gamma _{T,T}^{d,d} &{}0 &{}\gamma _{T,D}^{d,~} &{}0\\ 0 &{}0 &{}0 &{}\gamma _{T,S}^{\tau ,\tau } &{}0 &{}0 &{}0 &{}0 &{}0 &{}\gamma _{T,T}^{\tau ,\tau } &{}\gamma _{T,D}^{\tau ,~} &{}0\\ 0&{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}\gamma _{{D} ,D} &{}0\\ 0&{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0\\ \end{array} \right] \nonumber \\ \end{aligned}$$

(15)

where the first super- and subscript on the $\gamma$ submatrices belongs to the coefficient labelling the row, and the second indices identify the column. Section 5 runs up the dipole coefficient, for which the matrix ${\varvec{\Gamma }}_V$ is not required, so it will be given in a subsequent publication.

For QED mixing of four-fermion operators among themselves and to the dipole, the relevant diagrams are in Fig. 1, where the gauge boson is the photon, and $f_2 \in \{ u,d,s,c,b,e,\mu ,\tau \}$. These diagrams allow one to compute the $\gamma$-submatrices of Eq. (14). The results are given in Appendix B. For the second diagram of Fig. 1, $f_1 =e,\mu$, because Fierz transformations were used to obtain a basis where the $\mu$–e flavour change is within a spinor contraction.

4 At $m_W$

Above the “intermediate”, weak scale of the EFT, $m_W \simeq m_h \simeq m_t$, two things differ with respect to the low energy theory: the theory and non-renormalisable operators should now respect the weak SU(2) symmetry, and the particle content is extended to include the weak gauge bosons, the higgs, and the top. The additional requirement of SU(2) invariance will reduce the number of possible four-fermion operators, whereas adding new degrees of freedom (h, W, Z, t) allows more flavour-changing operators involving only two fermions.

4.0.1 Neglecting dimension-eight operators

The EFT above $m_W$ is an expansion in the inverse New Physics scale 1 / M, where the lowest order operators that are lepton flavour-changing, but number-conserving, appear at dimension six; they are listed in Appendix D. It is convenient to neglect the next order operators, which would appear at dimension eight, because they are numerous, and their RGEs are unknown. So it is interesting to explore how small must be the ratio v / M, to justify a parametrisation using dimension-six operators.

This question was studied for $\mu \rightarrow e \gamma$ in a 2 Higgs Doublet Model(2HDM) with LFV [64]. Naively, the dimension-eight operators are suppressed by $v^2/M^2\equiv z$. However, two enhancements arise:

• 1. In some cases, the dimension-six and -eight contributions arise at the same loop order, but the dimension-six part is from matching, whereas the dimension-eight term arises in running and is log$^2$-enhanced. The ratio of dimension six to eight is then $\propto z\ln ^2 z$, which is ${\sim }0.2$ for $M \sim 10 v$.

• 2. The couplings of the New Physics are unknown, and could have steep hierarchies. In the 2HDM, the heavy Higgs couplings to light fermions can be $\mathcal{O}(1)$, rather than of order the fermions’ SM Yukawa coupling. This increase is parametrised in the 2HDM by $\tan \beta$, which in some cases enhances the dimension-eight operators with respect to dimension six. In some 2HDMs, $\tan \beta \lesssim 50$, which I take as a reasonable estimate of the possible hierarchy of couplings between dimension-six and either operators.

In a generic model, these two enhancements could combine, and other sources of enhancement could perhaps arise. So I impose the requirement that $M \gtrsim 20$ TeV (${\sim }100v$), in the hope that this suppresses dimension-eight operators in many models.

4.1 Tree matching onto SU(2)-invariant operators

The coefficients of the four-fermion operators from below $m_W$, given in Eqs. (1) and (2), should be matched at $m_W$ onto the coefficients of the SU(2)-invariant BWP basis, which are listed in Appendix D. The coefficients on the left of the equalities are from below $m_W$, the coefficients on the right are SU(2) invariant. Both sets of coefficients should be evaluated at $m_W$, and the fermion masses which appear in the matching conditions should also be evaluated at $m_W$.

4.1.1 Dipoles

Above $m_W$, there is a dimension-six dipole operator for hypercharge, and another one for SU(2). They are given in Eqs. (100) and (101). The coefficient of the photon dipole operators $\mathcal{O}^{e \mu }_{D,R}$,$\mathcal{O}^{e \mu }_{D,L}$ from below $m_W$ are the linear combinations (the photon is $A^\alpha = c_W B^\alpha + s_W W^\alpha _3$, and the negative sign is from $\tau _3$):

$$\begin{aligned} C^{e\mu }_{D,R} = c_W C^{e\mu }_{eB} -s_W C^{e\mu }_{eW},\quad C^{e\mu }_{D,L} = c_W C^{ *\mu e}_{eB} -s_W C^{ *\mu e}_{eW}. \end{aligned}$$

However, rather than using the Hypercharge and SU(2) dipoles $\mathcal{O}^{e \mu }_{eB}$ and $\mathcal{O}^{e \mu }_{eW}$, I follow [43], and use the photon and Z dipoles above $m_W$, merely changing the names of the photon dipole coefficient

$$\begin{aligned} C^{ij}_{D,R}= & {} C^{ij}_{e \gamma } = c_W C^{ij}_{eB} -s_W C^{ij}_{eW},\nonumber \\ C^{ij}_{e Z}= & {} -s_W C^{ ij }_{eB} -c_W C^{ ij }_{eW} \end{aligned}$$

(16)

where $ij \in \{ e\mu , \mu e \}$. (Notice that since the operators are $\mathcal{O}^{e\mu }_{D,R }$ and $\mathcal{O}^{\mu e}_{D,R }$, the $+.h.c.$ gives the $\mathcal{O}^{ij}_{D,L }$).

4.1.2 Four-lepton operators

The BWP basis contains only the “vector” four-lepton operators given in Eqs. (94), (95) and (96). There are also new dimension-six interactions of the W, Z and h, described by the operators of Eqs. (102), (103), (104) and (99), which will contribute to four-lepton operators below $m_W$ in matching out the Z and h.

There are a few curiosities related to the flavour index structure below and above $m_W$. First, since the basis below $m_W$ was defined with the e–$\mu$ indices inside a spinor contraction, there is a scalar operator from below $m_W$ which must be Fierzed as given in Eq. (98). Also, there are more distinct flavour structures for operators constructed with SU(2) doublets, than singlets: the SU(2)-invariant operators $\mathcal{O}^{e \mu ff}_{L L}$ and $\mathcal{O}^{e ff \mu }_{L L}$, both match onto the below-$m_W$ operator $\mathcal{O}^{e \mu ff}_{L L}$. However, the two SU(2) operators are distinct² for $f =\tau$, but not for $f = e,\mu$.

The coefficients of operators from below $m_W$ (on the left of the equalities) can be matched as follows onto the SU(2)-invariant coefficients to the right:

$$\begin{aligned} C^{e \mu ll}_{RR}= & {} C^{e \mu ll}_{EE} - 2 C^{e \mu }_{HE} g_R^e , \end{aligned}$$

(17)

$$\begin{aligned} C^{e \mu \tau \tau }_{RR}= & {} C^{e \mu \tau \tau }_{EE} - C^{e \mu }_{HE} g_R^e , \end{aligned}$$

(18)

$$\begin{aligned} C^{e \mu \ell \ell }_{LR}= & {} C^{e \mu \ell \ell }_{LE} - \left( C^{e \mu }_{HL,3} + C^{e \mu }_{HL,1}\right) g_R^e , \end{aligned}$$

(19)

$$\begin{aligned} C^{e \mu \ell \ell }_{RL}= & {} C^{\ell \ell e \mu }_{LE} - C^{e \mu }_{HE} g_L^e \end{aligned}$$

(20)

$$\begin{aligned} C^{e \mu \tau \tau }_{LL}= & {} C^{e \mu \tau \tau }_{LL} + C^{e \tau \tau \mu }_{LL} -\left( C^{e \mu }_{HL,3} + C^{e \mu }_{HL,1}\right) g_L^e , \end{aligned}$$

(21)

$$\begin{aligned} C^{e \mu ll}_{LL}= & {} C^{e \mu ll}_{LL} -2\left( C^{e \mu }_{HL,3} + C^{e \mu }_{HL,1}\right) g_L^e , \end{aligned}$$

(22)

$$\begin{aligned} C^{e \mu \ell \ell }_{S,RR}= & {} - \frac{m_\ell C^{e \mu }_{EH} v}{m_h^2}, \end{aligned}$$

(23)

$$\begin{aligned} C^{e \mu \tau \tau }_{S,LR}= & {} -2 C_{LE}^{\tau \mu e \tau } - \frac{m_\tau C^{ \mu e *}_{EH} v}{m_h^2}, \end{aligned}$$

(24)

$$\begin{aligned} C^{e \mu \tau \tau }_{S,RL}= & {} -2 C_{LE}^{e \tau \tau \mu } - \frac{m_\tau C^{e \mu }_{EH} v}{m_h^2}, \end{aligned}$$

(25)

$$\begin{aligned} C^{e \mu \ell \ell }_{S,LL}= & {} - \frac{m_\ell C^{ \mu e * }_{EH} v}{m_h^2} , \end{aligned}$$

(26)

$$\begin{aligned} C^{e \mu \tau \tau }_{T,RR}= & {} 0 , \end{aligned}$$

(27)

$$\begin{aligned} C^{e \mu \tau \tau }_{T,LL}= & {} 0, \end{aligned}$$

(28)

where $\ell \in \{e,\mu ,\tau \}$, $l \in \{e,\mu \}$, $s_W = \sin \theta _W$, and the Feynman rule for Z couplings to leptons is $i \frac{g}{2 c_W}(g^e_L P_L + g^e_R P_R)$, with

$$\begin{aligned} g_R^e = -2 s_W^2,\quad g_L^e = 1-2 s_W^2. \end{aligned}$$

(29)

In the case of vector operators involving three muons or three electrons of the same chirality, there can be two Z-exchange diagrams (u and t channel), which can give a 2 with respect to operators involving $(\bar{e}\mu ) (\bar{\tau }\tau )$. From Eq. (27) and (28), the tensor coefficients vanish at tree matching. Nonetheless, these operators are important below $m_W$, because as seen in the previous section, scalars mix to tensors, and tensors to the dipole.

4.1.3 Two-lepton–two-quark operators

Two issues about the CKM matrix V arise in matching operators involving quarks at $m_W$: does V appear in the coefficients above or below $m_W$, and are the quark doublets in the u or d mass basis? I put V in the coefficients above $m_W$, because the experimental constraints are being matched “bottom-up” onto operator coefficients. So one coefficient from below $m_W$ will match onto a sum of coefficients above $m_W$, weighted by CKM matrix elements. Secondly, the quark doublets above $m_W$ are taken in the u, c, t mass eigenstate basis, because it is convenient for translating up in scale the bound on $\mu \rightarrow e \gamma$, as will be done in Sect. 5. This is because tensor operators mix to the dipoles, and only for u-type quarks are there SU(2)-invariant dimension-six tensors operators.

The BWP basis of two-lepton–two-quark operators has seven vector operators given in Eqs. (81), (82), (83), (84), (85), (86), (87) and two scalars and a tensor given in Eqs. (88), (89), (90), (91), (92) and (93). For the first two generations and the b quark, the coefficents from below $m_W$ (left side of equality) can be matched to the coefficients above $m_W$ as follows:

$$\begin{aligned} C^{e \mu u_n u_n}_{LL}= & {} C^{e \mu nn}_{LQ (1)} - C^{e \mu nn}_{LQ (3)} - g^u_L \left( C^{e \mu }_{HL (1)} + C^{e \mu }_{HL (3)}\right) , \nonumber \\&\end{aligned}$$

(30)

$$\begin{aligned} C^{e \mu d_n d_n}_{LL}= & {} \sum _{jk} V_{jn} V^*_{kn} \left( C^{e \mu jk}_{LQ (1)} + C^{e \mu jk}_{LQ (3)}\right) \nonumber \\&- g^d_L \left( C^{e \mu }_{HL (1)} + C^{e \mu }_{HL (3)} \right) , \end{aligned}$$

(31)

$$\begin{aligned} C^{e \mu u_n u_n}_{RR}= & {} C^{e \mu nn}_{EU} - g^u_R C^{e \mu }_{HE}, \end{aligned}$$

(32)

$$\begin{aligned} C^{e \mu d_n d_n}_{RR}= & {} C^{e \mu nn}_{ED} - g^d_R C^{e \mu }_{HE}, \end{aligned}$$

(33)

$$\begin{aligned} C^{e \mu u_n u_n}_{LR}= & {} C^{e \mu nn}_{LU} - g^u_R \left( C^{e \mu }_{HL (1)} + C^{e \mu }_{HL (3)} \right) , \end{aligned}$$

(34)

$$\begin{aligned} C^{e \mu d_n d_n}_{LR}= & {} C^{e \mu nn}_{LD}- g^d_R \left( C^{e \mu }_{HL (1)} + C^{e \mu }_{HL (3)} \right) , \end{aligned}$$

(35)

$$\begin{aligned} C^{e \mu u_n u_n}_{RL}= & {} C^{e \mu nn}_{EQ} - g^u_L C^{e \mu }_{HE}, \end{aligned}$$

(36)

$$\begin{aligned} C^{e \mu d_n d_n}_{RL}= & {} \sum _{jk} V_{jn} V^*_{kn} C^{e \mu jk}_{EQ} - g^d_L C^{e \mu }_{HE}, \end{aligned}$$

(37)

$$\begin{aligned} C^{e \mu u_nu_n}_{S,LL}= & {} C_{LEQU}^{* \mu e nn} - \frac{m_{u_n} v}{m_h^2} C^{ \mu e *}_{EH}, \end{aligned}$$

(38)

$$\begin{aligned} C^{e \mu d_n d_n}_{S,LL}= & {} - \frac{m_{d_n} v}{m_h^2} C^{ \mu e *}_{EH} , \end{aligned}$$

(39)

$$\begin{aligned} C^{e \mu u_n u_n}_{S,RR}= & {} C_{LEQU}^{e \mu nn} - \frac{m_{u_n} v}{m_h^2} C^{ e \mu }_{EH}, \end{aligned}$$

(40)

$$\begin{aligned} C^{e \mu d_n d_n}_{S,RR}= & {} - \frac{m_{d_n} v}{m_h^2} C^{e \mu }_{EH}, \end{aligned}$$

(41)

$$\begin{aligned} C^{e \mu u_n u_n}_{S,LR}= & {} - \frac{m_{u_n} v}{m_h^2} C^{ \mu e * }_{EH}, \end{aligned}$$

(42)

$$\begin{aligned} C^{e \mu d_n d_n}_{S,LR}= & {} C_{LEDQ}^{* \mu e nn} - \frac{m_{d_n} v}{m_h^2} C^{ \mu e * }_{EH}, \end{aligned}$$

(43)

$$\begin{aligned} C^{e \mu u_n u_n}_{S,RL}= & {} - \frac{m_{u_n} v}{m_h^2} C^{ e \mu }_{EH}, \end{aligned}$$

(44)

$$\begin{aligned} C^{e \mu d_n d_n}_{S,RL}= & {} C_{LEDQ}^{e \mu nn} - \frac{m_{d_n} v}{m_h^2} C^{ e \mu }_{EH}, \end{aligned}$$

(45)

$$\begin{aligned} C^{e \mu u_n u_n}_{T,LL}= & {} C_{T,LEQU}^{* \mu e nn}, \end{aligned}$$

(46)

$$\begin{aligned} C^{e \mu d_n d_n}_{T,LL}= & {} 0, \end{aligned}$$

(47)

$$\begin{aligned} C^{e \mu u_n u_n}_{T,RR}= & {} C_{T,LEQU}^{e \mu n n}, \end{aligned}$$

(48)

$$\begin{aligned} C^{e \mu d_n d_n}_{T,RR}= & {} 0, \end{aligned}$$

(49)

where $u_n \in \{u,c \}$, $d_n \in \{d,s,b \}$, and

$$\begin{aligned}&g^u_L = 1-\frac{4}{3} s_W^2,~~ g^u_R = -\frac{4}{3} s_W^2,\nonumber \\&g^d_L = -1+\frac{2}{3} s_W^2,~~ g^d_R = \frac{2}{3} s_W^2. \end{aligned}$$

(50)

4.2 Comments on tree matching

One observes that the consequences of matching at $m_W$, at tree level, are different for vector vs. scalar–tensor-dipole operators. In the vector case, there are more operator coefficients in the SU(2)-invariant theory above $m_W$ than in the QCD$\times$QED-invariant theory below, whereas there are fewer for the scalar–tensor operators. This means that SU(2)-invariance should predict some correlations in the scalar–tensor coefficients below $m_W$. Whereas, if one was trying to reconstruct the coefficients of the SU(2)-invariant operators from data, some additional input (e.g. from Z physics, neutrino interactions [52], or loop matching) would be required for the vector operators, beyond the coefficients of the operators of Eqs. (1) and (2).

4.2.1 The vector operators

Consider first the vector operators, including the “penguin” operators of Eqs. (102), (103) and (104) as well as the four-fermion operators.

• In the case of four-lepton operators with flavour indices $e \mu ee$ or $e\mu \mu \mu$, there are the same number of independent coefficients above and below. There is one extra four-lepton operator above $m_W$ for flavour indices $e\mu \tau \tau$, as can be seen from Eq. (21).

• There are fewer two-lepton–two-quark operator coefficients above $m_W$ than below. It is clear that the operators $\mathcal{O}_{LR}^{e \mu qq}$, $\mathcal{O}_{RR}^{e \mu qq}$ from below $m_W$ with $q \in \{u,d,s,c,b\}$ are equivalent to the $\mathcal{O}_{LU}^{e \mu u_nu_n}$, $\mathcal{O}_{LD}^{e \mu d_nd_n}$, $\mathcal{O}_{EU}^{e \mu u_nu_n}$, $\mathcal{O}_{ED}^{e \mu d_nd_n}$ operators from above. Also it is clear that the $\mathcal{O}_{LL}^{e \mu qq}$ from below $m_W$ with $q \in \{u,d,c,s,b\}$ have the same number of independent coefficients as $\mathcal{O}_{LQ (1)}^{e \mu nn}$ and $\mathcal{O}_{LQ (3)}^{e \mu nn}$. The restriction occurs between $\mathcal{O}_{RL}^{e \mu qq}$ from below $m_W$, where there are five coefficients corresponding to $q \in \{u,d,s,c,b\}$, and $\mathcal{O}_{EQ}^{e \mu nn}$ above $m_W$, which has a coefficient per generation. Neglecting CKM sums, this suggests that SU(2) predicts the $C_{RL}^{e \mu uu} - C_{RL}^{e \mu dd}=0$ and $C_{RL}^{e \mu cc} - C_{RL}^{e \mu ss} = 0$; however, there is a penguin operator which contribute to both differences, so only the difference of differences is an SU(2) prediction (possibly blurred by CKM).

• The “penguin” operators from above $m_W$ (see Eqs. (102), (103), (104)) give the Z a vertex with $\bar{e} \gamma P_Y \mu$, which matches onto $(\bar{e} \gamma P_Y \mu ) (\bar{f} \gamma P_X f)$ operators for all the SM fermions below $m_W$, in ratios fixed by the SM Z couplings. This contribution adds to the four-fermion operator induced at the scale M in the EFT, as given in the matching conditions Eqs. (17)–(30). So the coefficient of the $\bar{e} \, Z \! \! \! \! / ~ P_R \mu$ penguin operator of Eq. (104) could be determined from $C_{RL}^{e \mu uu} - C_{RL}^{e \mu dd}$, as discussed in the item above. The coefficients of the two remaining penguin operators are “extra”: in naive coefficient-counting, there are two more vector coefficients above $m_W$ than below. However, they are not completely “free”, because they would match at one loop onto the photon dipole operator at $m_W$. These extra penguins are related to the common wisdom, that it is interesting for ATLAS and CMS to look for $Z \rightarrow \tau ^\pm \mu ^\mp$ and $Z \rightarrow \tau ^\pm e^\mp$ decays, but that they are unlikely to see $Z \rightarrow \mu ^\pm e^\mp$ [53]. The point [54] is that an interaction $\bar{\tau } \, Z \! \! \! \! / ~ \mu$ would contribute at tree level to $\tau \rightarrow \mu \bar{l}l$, and at one loop to $\tau \rightarrow \mu \gamma$. To be within the sensitivity of the LHC, the coefficient of this coupling needs to exceed the naive bound from $\tau \rightarrow \mu \bar{l}l$. However, $BR(\tau \rightarrow 3l )$ [55] is controlled by coefficients $C_{XY}^{\mu \tau ll}$, $C_{YY}^{\mu \tau ll}$, analogous to the coefficients on the left of Eqs. (17)–(22), which are the sum of SU(2)-invariant four-fermion and penguin coefficients. So the penguin coefficient could exceed the expected bound from $\tau \rightarrow 3l$, provided that it is tuned against the four-fermion coefficient.³ This same argument could apply to a $\bar{e} \, Z \! \! \! \! / ~ \mu$ coupling and the bound from $\mu \rightarrow e \bar{e} e$, although more tuning would be required, since the bound on $\mu \rightarrow e \bar{e} e$ [57] is more restrictive. However, the Z penguins also contribute at one loop to $\mu \rightarrow e \gamma$ and $\tau \rightarrow \mu \gamma$. And whereas the experimental constraint on $\tau \rightarrow \mu \gamma$ [58, 59] is consistent with $Z \rightarrow \tau ^\pm \mu ^\mp$ being detectable at the LHC, the bound from $\mu \rightarrow e \gamma$ implies that a $\bar{e} \, Z \! \! \! \! / ~ \mu$ interaction, with coefficient of a magnitude that the LHC could detect, would overcontribute to $\mu \rightarrow e \gamma$ by several orders of magnitude [54].

4.2.2 The scalar, tensor and dipole operators

• Above $m_W$, there are two dipoles, given in Eq. (16). At tree level, the Z-dipole does not match onto any operator below $m_W$.

• There are no dimension-six, SU(2)-invariant four-fermion operators to match onto the tensor operators $\mathcal{O}^{e\mu ff}_{T,YY}$ for $f \in \{ \tau ,d,s,b\}$. Furthermore, in tree level matching, the tensors are not generated by any heavy particle exchange. They are presumeably generated in one-loop matching by the same diagrams that give the mixing below $m_W$, but this should be subdominant because the log is lacking.

• There are no dimension-six, SU(2)-invariant four-fermion operators to match onto the scalar operators $\mathcal{O}^{e\mu u_nu_n}_{S,YX}$ and $\mathcal{O}^{e\mu ff}_{S,YY}$ for $f \in \{ e,\mu ,\tau ,d,s,b\}$, $u_n \in \{ u,c\}$ and $X\ne Y$. However, SM Higgs exchange, combined with the $H^\dagger H \bar{L}HE$ operator, will generate these operators in tree matching, weighted by $m_f v/m_h^2$ or $m_{u_n} v/m_h^2$. So it is a tree-level SU(2) prediction that these coefficients are small, as noted by [60]. Since the coefficients of scalar operators involving quarks are normalised by a running quark mass, see Eq. (12), one obtains $C^{e\mu ff}_{S,\ldots } (m_\tau ) \simeq -C^{e\mu }_{EH} (m_W) m_f(m_\tau ) m_t/m_h^2$.

4.2.3 Matching at “Leading” order

The aim of a bottom-up EFT analysis is to translate the bounds from several observables to combinations of operator coefficients at the high scale. So one must compute the numerically largest contribution of each operator to several observables ($\mu \rightarrow e \gamma$, $\mu \rightarrow e ~\mathrm{conversion}$ and $\mu \rightarrow e \bar{e} e$, in the case of $\mu$–e flavour change). It is interesting to have constraints from different observables, rather than just the best bound, because there are more operators than observables, so a weaker constraint on a different combination of coefficients can reduce degeneracies. However, in this paper, only the experimental bound from $\mu \rightarrow e \gamma$ is considered, so the aim is to obtain the best bound it sets on all operator coefficients.

In the next section, we will see that tree matching and one-loop running, as performed so far, do not reproduce the correct constraints from $\mu \rightarrow e \gamma$ on the operators which parametrise LFV interactions of the Higgs and Z; that is, the numerically dominant contributions of these operators to $\mu \rightarrow e \gamma$ are not included. In addition, two-loop QED running [42] is required below $m_W$ to obtain bounds on vector operators. So it is clear that the simplistic formalism given here, of tree matching and one-loop running, does not work for $\mu \rightarrow e \gamma$. It would be interesting to construct a systematic formalism, gauge-invariant and renormalisation scheme independent, that allows one to obtain the best bound on each operator from each observable. I suppose that such a formalism corresponds to “leading order”. Notice that leading order is only defined “top-down”, because it describes the contribution of an operator to an observable. So to construct a LO formalism for bottom-up EFT, it seems that one must work top-down, finding the numerically dominant contribution of each operator to each observable, then ensuring that the combination of the contributions from all the operators is scheme independent.

As previously stated, the LO two-loop running is neglected in this paper. However, some attempt is made to perform LO matching at $m_W$, where the “LO contribution” of a coefficient above the matching scale to a coefficient below, is pragmatically defined as the numerically dominant term (and not the lowest order in the loop expansion, because this may not be the numerically dominant contribution in presence of hierarchical Yukawas).

So, in summary, the “leading order” matching performed for $\mu \rightarrow e \gamma$ in the next section will consist of the tree equivalences given in this section, augmented by some one- and two-loop contributions of operators that do not mix to the dipole. These loop contributions are obtained by listing all the operators which do not mix into the dipole above $m_W$, estimating their matching contribution at $m_W$, and including it if it gives an interesting constraint.

5 Translating the $\mu \rightarrow e \gamma$ bound to $M > m_W$

In this section, the aim is to use the machinery developed in the previous sections to translate the experimental bound on $BR(\mu \rightarrow e \gamma )$ to a constraint on operator coefficients at the New Physics scale M.

5.1 Parametrising $\mu \rightarrow e \gamma$

A flavour-changing dipole operator (in the notation of Kuno and Okada [1])

$$\begin{aligned} \mathcal{L}_{\mu \rightarrow e \gamma } \!=\! -\!\frac{4G_F}{\sqrt{2}} m_\mu \left( A_R \overline{\mu _R} \sigma ^{\alpha \beta } e_L F_{\alpha \beta } \!+\! A_L \overline{\mu _L} \sigma ^{\alpha \beta } e_R F_{\alpha \beta }\right) \nonumber \\ \end{aligned}$$

(51)

can be added to the SM Lagrangian at a low scale $\sim m_\mu$, and gives a branching ratio

$$\begin{aligned} BR(\mu \rightarrow e \gamma )= 384 \pi ^2 (|A_R|^2 + |A_L|^2) <5.7\times 10^{-13}\nonumber \\ \end{aligned}$$

(52)

where the constraint is from the MEG experiment [61]. If $|A_R| = |A_L|$, then $|A_X| <8.6\times 10^{-9}$, whereas conservatively only allowing for one coefficient gives the bound $|A_X| <1.2\times 10^{-8}.$ Translated to the coefficients of the dipole operators of Eq. (1), which are defined including a muon Yukawa, this conservative limit gives

$$\begin{aligned} C^{e\mu }_{D,X} = \frac{ A_X M^2}{m_t^2} <1.2\times 10^{-8} \frac{ M^2}{m_t^2}. \end{aligned}$$

(53)

It is interesting to estimate the scale M to which experiments currently probe. One can consider three possible guesses for the form of the coefficient of the operator $\bar{\mu } \sigma \cdot F P_X e$:

$$\begin{aligned} c\frac{m_\mu }{M^2},~~~ c\frac{v}{M^2},~~~ c\frac{e v}{16 \pi ^2 M^2}, \end{aligned}$$

(54)

where $c\lesssim 1$ is a dimensionless combination of numerical factors and couplings constants. The first guess is the Kuno–Okada normalisation of (51), corresponding to the Higgs leg attached to the muon line, but a tree diagram, and suggests that the current data probes scales up to $\sim 10^{6}$ GeV. The second guess gives the maximum possible scale of $\sim 10^{8}$ GeV – however, it supposes the dipole operator is generated at tree level, with all couplings ${\sim }1$. The final guess takes into account that the dipole operator is generated at one loop with a photon leg, and gives a maximum scale of $M \lesssim 3 \times 10^{6}$ GeV. Notice that this guess is very similar to the Kuno–Okada normalisation used to define the dipoles in this paper: $e/(16\pi ^2) \sim 3 y_\mu$. The maximum scale is relevant, because it determines how large can be the logarithm from the RGEs above $m_W$. I take the third guess with

$$\begin{aligned} M \lesssim 3 \times 10^{6}~\mathrm{GeV} ~~~ \Rightarrow ~~~ \ln \frac{M}{m_W} \lesssim 10. \end{aligned}$$

(55)

It is also interesting to estimate the loop order probed by the current MEG bound. Counting $1/(16 \pi ^2)$ for a loop (as if couplings$\times$logarithm $\simeq$ 1), and assuming that $M\gtrsim 10$ TeV (beyond the reach of the LHC), then Eq. (55) suggests that three-loop effects could be probed. In Sect. 5.4, estimated bounds are given on all the operators which MEG can constrain. Four-fermion operators are defined to be “constrainable” if their coefficients C can be bounded $C \lesssim 1$ at a scale $M \sim 100 m_t$. It turns that all these operators are within two SM loops of the dipole.

5.2 Running up to $m_W$

Between $m_W$ and $m_\tau$, various operators mix into the dipole, so at $m_W$, the exptal bound (53) applies to the linear combination of the coefficients given on the left-hand-side of Eq. (4), when the dummy index B is taken to be a dipole:

$$\begin{aligned} \vec {C}_D(m_\tau )= & {} \vec {C}_D(m_W) - \frac{\alpha }{4\pi } \left\{ \sum _{l=e,\mu } \vec {C}_{Sl}(m_W) \left[ \gamma ^l_{SD}\right] \right. \nonumber \\&\left. +\sum _{x=q_i,u,d,\tau } \left( \vec {C}^x_T(m_W) - \frac{\alpha }{8\pi } \log \frac{m_W}{m_\tau } \right. \right. \nonumber \\&\times \left. \phantom {\left\{ \sum _{l=e,\mu } \vec {C}_{Sl}(m_W) \left[ \gamma ^l_{SD}\right] \right. }\left. \phantom {\left( \vec {C}^x_T(m_W) - \frac{\alpha }{8\pi } \log \frac{m_W}{m_\tau } \right. }\vec {C}^x_S (m_W)\left[ \gamma ^x_{ST}\right] \right) \left[ \gamma ^x_{TD}\right] \right\} \log \frac{m_W}{m_\tau } \end{aligned}$$

(56)

where $q_i \in \{s,c,b\}.$ The contribution of $C^{e\mu ee}_{S,LL}(m_W)$ will be neglected, because it is constrained by $\mu \rightarrow e \bar{e} e$. A linear combination of $C^{e\mu dd}_{S,LL}(m_W)$ $C^{e\mu ss}_{S,LL}(m_W)$, and $C^{e\mu uu}_{S,LL}(m_W)$ contributes to $\mu \rightarrow e ~\mathrm{conversion}$, so possibly an independent constraint from $\mu \rightarrow e \gamma$ on a different combination could be interesting. However, I neglect these coefficients too, to avoid strong interaction issues and because in tree matching at $m_W$, the first two are Yukawa suppressed to irrelevance.⁴ In the following, I focus on the “left-handed” dipole $C_{D,L}^{e\mu }$. The evolution of $C_{D,R}^{e\mu }$ is similar, so for the “right-handed dipole”, only final results and a few non-trivial differences are given (which arise due to Higgs loops above $m_W$, where $Y_e \ll Y_\mu$ is neglected). One obtains

$$\begin{aligned} C^{e\mu }_{D,L}(m_\tau )\simeq & {} C^{e\mu }_{D,L}(m_W) + \frac{e}{4\pi ^2}\left( \phantom {\left. + \frac{8 m_\tau }{m_\mu } C^{e\mu \tau \tau }_{T,LL}(m_W) \right) }C^{e\mu \mu \mu }_{S,LL}(m_W) \right. \nonumber \\&- \frac{8 Q_u N_c m_u }{m_\mu } C^{e\mu uu}_{T,LL}(m_W) + \frac{8 m_d }{ m_\mu } C^{e\mu dd}_{T,LL}(m_W) \nonumber \\&+ \frac{8 m_s}{m_\mu } C^{e\mu ss}_{T,LL}(m_W)\nonumber \\&\left. - \frac{8 Q_u N_c m_c }{m_\mu } C^{e\mu cc}_{T,LL}(m_W) + \frac{8 m_b }{ m_\mu } C^{e\mu bb}_{T,LL}(m_W) \right. \nonumber \\&\left. + \frac{8 m_\tau }{m_\mu } C^{e\mu \tau \tau }_{T,LL}(m_W) \right) \nonumber \\&+\frac{ e \alpha }{\pi ^3} \left( \phantom {\left. + \sum _{q = s,c,b}\frac{2 N_c Q_q^2 m_q }{m_\mu } C^{e\mu qq}_{S,LL}(m_W) \right) } + \frac{2 m_\tau }{m_\mu } C^{e\mu \tau \tau }_{S,LL}(m_W) \right. \nonumber \\&\left. + \sum _{q = s,c,b}\frac{2 N_c Q_q^2 m_q }{m_\mu } C^{e\mu qq}_{S,LL}(m_W) \right) \end{aligned}$$

(57)

where the first parenthesis is first order in ${\varvec{\Gamma }}$, the second parenthesis is the second order scalar$\rightarrow$tensor$\rightarrow$dipole mixing, $Q_q$ is the electric charge, and the $\log \frac{m_W}{m_\tau }$ was taken $\sim 4$. The light quark (u, d, s) tensor contributions only include the mixing between $m_W$ and $m_\tau$; the (non-perturbative) mixing between $m_\tau$ and $m_\mu$ is difficult to calculate, so neglected. Due to this uncertainty, the light quark tensors are neglected after Eq. (58). With quark masses evaluated at $m_W$, this gives

$$\begin{aligned}&C^{e\mu }_{D,L}(m_\tau )\simeq C^{e\mu }_{D,L}(m_W)-.0016C^{e\mu uu}_{T,LL}(m_W)\nonumber \\&\quad +.0017C^{e\mu dd}_{T,LL}(m_W)+0.35C^{e\mu ss}_{T,LL}(m_W) \nonumber \\&\quad - 1.0 C^{e\mu cc}_{T,LL}(m_W) + 1.0 C^{e\mu \tau \tau }_{T,LL}(m_W) + 1.8 C^{e\mu bb}_{T,LL}(m_W) \nonumber \\&\quad + 10^{-3} \left\{ 7.6 C^{e\mu \mu \mu }_{S,LL}(m_W) + 4.6 C^{e\mu \tau \tau }_{S,LL}(m_W) ~~ \right. \nonumber \\&\quad \left. +1.4 C^{e\mu bb}_{S,LL}(m_W) +1.5 C^{e\mu cc}_{S,LL}(m_W) \right\} ~~~~ \end{aligned}$$

(58)

where one notices that the scalar$\rightarrow$tensor$\rightarrow$dipole mixing of the “heavy” fermion ($f \in \{\tau ,c,b \}$) operators is of the same magnitude as the scalar$\rightarrow$dipole mixing of the $\mu$ operator, because the anomalous dimension mixing tensors to dipoles is large and enhanced by $m_f/m_\mu$. This mixing is the EFT implementation of the two-loop “Barr–Zee” diagrams (see Fig. 3) of the $\tau$, c and b: contracting the scalar propagator of the Barr–Zee diagram to a point gives a scalar four-fermion operator, then the photon exchanged between the muon and heavy fermion makes a tensor operator, then the heavy fermion lines are closed to give the dipole.

At the weak scale, the experimental bound constrains a linear combination of several different operators. It is common to quote the resulting constraints “one at a time”, that is, retaining only one coefficient in the sum of Eq. (58), and setting the remainder to zero, in order to obtain a bound. I will do this later, in listing bounds at the scale M. However, it is important to remember that the MEG experiment only ever gives two constraints (on $C^{e\mu }_{D,R}(m_\tau )$ and $C^{e\mu }_{D,L}(m_\tau )$) in the multi-dimensional space of operator coefficients, and additions or cancellations are possible among the many contributing operators at $m_W$. This is illustrated in Fig. 2, where the black lines give the experimental bound at low energy on $C^{e\mu }_{D,L}(m_\tau )$. The diagonal blue lines are the bound at $m_W$, in a model where only the coefficients $C^{e\mu }_{D,L}(m_W)$ and $C^{e\mu cc}_{T,LL}(m_W)$ are non-zero: arbitrarily large values of $C^{e\mu }_{D,L}(m_W)$ and $C^{e\mu cc}_{T,LL}(m_W)$ are allowed, provided they are correlated. Including experimental constraints from $\mu \rightarrow e \bar{e} e$ and $\mu \rightarrow e ~\mathrm{conversion}$ would give other constraints on different linear combinations of coefficients, but the problem of having more operators than experimental constraints would remain.

Fig. 2

Between the vertical black lines is the allowed range for the coefficients of the dipole operator $\mathcal{O}_{D,X}^{e \mu }$ (horizontal axis) and c-tensor operator $\mathcal{O}_{T,XX}^{e \mu cc}$ (vertical axis), evaluated at low energy. At $m_W$, the allowed region is between the diagonal blues lines; see Eq. 58. This illustrates that the allowed region changes with scale, in this case due to operator mixing

5.3 Matching at $m_W$

The tree-level matching conditions of Sect. 4 allow one to translate, at $m_W$, the coefficients of QCD$\times$QED-invariant operators to SU(2)-invariant coefficients. With these rules, the low-scale dipole coefficient can be written

$$\begin{aligned} C^{e\mu }_{D,L}(m_\tau )\simeq & {} C^{\mu e *}_{e \gamma }(m_W) - C^{\mu e cc *}_{LEQU (3)}(m_W)\frac{2 e Q_u N_c m_c }{m_\mu \pi ^2} \nonumber \\&+ C^{\mu e cc *}_{LEQU}(m_W)\frac{2 e \alpha Q_u^2 N_c m_c }{m_\mu \pi ^3} \nonumber \\&-C^{\mu e *}_{EH}(m_W) \left[ \frac{ m_\mu v }{4 \pi ^2m_h^2} + \frac{2 e \alpha }{\pi ^3}\frac{ m^2_\tau v }{m_\mu m_h^2 } \right. \nonumber \\&\left. + \frac{2 e \alpha N_c v }{ \pi ^3 m_h} \left( \frac{Q_d^2 m_b^2 + Q_u^2 m_c^2}{m_\mu m_h}\right) \right] , \end{aligned}$$

(59)

with a similar equation for $C^{e \mu }_{D,R}(m_\tau )$. Only four SU(2)-invariant coefficients are required, because for the leptons and down-type quarks, there are no SU(2)-invariant, dimension-six tensor operators, nor scalar operators with the required LL chiral structure. The tensor operators are not generated in matching out the W, Z, h and t at tree level, so their coefficients can be set to zero as given in Eqs. (27), (28), (47) and (49). (They could arise in one-loop matching, via diagrams similar to those giving running below $m_W$, so the tensor coefficients were retained in the discussion of the Sect. 5.2.) The scalar operators are generated in matching out the Higgs, see Sect. 4.1, which gives the square bracket above.

Fig. 3

The two-loop “Barr–Zee” diagrams which gives the largest contribution of the $H^\dagger H \bar{L} HE$ operator to the dipole below $m_W$. The grey disk is the dimension-six interaction, with two Higgs legs connecting to the vev. The Higgs line approaching the top loop indicates a mass insertion somewhere on the top loop

However, it is well known that this estimate has missed the largest contribution from $\mathcal{O}^{\mu e *}_{EH}$ to the dipole operator below $m_W$, which are “Barr–Zee” diagrams with the SM Higgs and a top or W loop, as illustrated in Fig. 3. Despite being suppressed by two loops, these diagrams are enhanced by $m^2_t/m^2_\mu$ or $m^2_W/m^2_\mu$. In SU(2)-invariant notation, these diagrams generate a “dimension-eight” dipole $H^\dagger H \bar{L} H\sigma \cdot F E$. However, SU(2) is irrelevant below $m_W$, so this is an $\mathcal{O}(1/M^2)$ matching contribution to $\mathcal{O}^{e \mu }_{D,X}$. For lack of good ideas on how to do a well-defined perturbation theory in many small parameters (in particular, loops and hierarchical Yukawas), I retrieve from the results of Chang et al. [62], the evaluation of the Barr–Zee diagrams with a SM Higgs and a top or W loop (which have opposite sign):

$$\begin{aligned} \Delta C^{e\mu }_{D,L}(m_W)\simeq & {} - C^{\mu e *}_{EH}(m_W) \left[ \frac{e\alpha }{16\pi ^3Y_\mu } \left( Q_t^2 N_c Y^2_t -\frac{7}{2} \right) \right] \nonumber \\\simeq & {} C^{\mu e *}_{EH}(m_W) \left[ \frac{e\alpha }{8\pi ^3Y_\mu } \right] \end{aligned}$$

(60)

and substitute the square brackets of Eq. (60) for those in eqn (59).

Having started cherry-picking the “leading” contributions from higher order, it is interesting also to include the one-loop matching contribution of the “penguin” operators of Eqs. (102), (103) and (104). These give a lepton-flavour-changing vertex to the Z, which contributes to $Z \rightarrow \mu ^\pm e^\mp$ and at one loop to $\mu \rightarrow e \gamma$. As discussed in Sect. 4.2, in the context of LHC searches for flavour-changing Z decays, $\mu \rightarrow e \bar{e} e$ give a restrictive bound on a combination of the penguins plus four fermion operators. So even if weaker, an independent constraint from $\mu \rightarrow e \gamma$, on a different combination of operators, is interesting. The one-loop diagram with a flavour-changing Z-penguin vertex, gives contributions to the dipole coefficients:

$$\begin{aligned} \Delta C^{\mu e *}_{e\gamma } (m_W)\simeq & {} \frac{e }{16\pi ^2} g^e_L C^{e \mu }_{HE} (m_W) \nonumber \\ \Delta C^{e \mu }_{e\gamma } (m_W)\simeq & {} \frac{e }{16\pi ^2} g^e_R \left( C^{e \mu }_{HL(1)} (m_W) + C^{e \mu }_{HL(3)} (m_W) \right) ,\nonumber \\ \end{aligned}$$

(61)

where $g^e_L, g^e_R$ are given in Eq. (29), no muon Yukawa appears in the matching coefficient because it is implicit in the dipole operator definition, and the electron Yukawa was neglected (which is why different penguins mix into the above two dipoles). The contribution $\Delta C^{\mu e *}_{e\gamma }$ is to be added to the right side of Eq. (59), and $\Delta C^{e \mu }_{e\gamma }$ should be added to the modification of Eq. (59) appropriate to $C_{D,R}^{e \mu }$.

5.4 Running up to M

At $m_W$, $C^{e \mu }_{D,L} (m_\tau )$ can be written as a linear combination of $C^{\mu e *}_{e\gamma }(m_W)$, $C^{\mu e *}_{eZ}(m_W)$, $C^{\mu e cc *}_{LEQU(1)}(m_W)$, $C^{\mu e cc *}_{LEQU(3)}(m_W)$, $C^{e \mu }_{HE}(m_W)$, and $C^{\mu e *}_{EH}(m_W)$. The RGEs to evolve these coefficients up to M are given in [39, 40, 43], and generate more intricate and extensive operator mixing than was present below $m_W$. The aim here is to present manageable analytic formulae that approximate the “leading” (= numerically most important) constraints on all the constrainable coefficients at the scale M. Recall that an operator coefficient was defined here to be constrainable if the current MEG bound, as given in Eq. (53), implies $C < 1$ at $M \simeq 100 m_t$.

Consider first $C^{\mu e *}_{EH}$. Neglecting its self-renormalisation between M and $m_W$, because the anomalous dimension $\times \ln M/m_W < 16 \pi ^2$, the “one-operator-at-a-time” constraint at $M \simeq 100 m_t$ is $C^{\mu e *}_{EH} \lesssim 0.01$. So there could be a bound on operators that mix into $\mathcal{O}^{\mu e *}_{EH}$ in running between M and $m_W$. These include the Z and $\gamma$ dipoles, which can be neglected here because they have more direct contributions to $\mu \rightarrow e \gamma$. There is also a $Y_\mu$-suppressed mixing from the “penguin” operators, which is neglected because the penguins match at one loop onto the dipole at $m_W$. So I approximate

$$\begin{aligned} C^{\mu e *}_{EH} (m_W) = C^{\mu e *}_{EH}(M). \end{aligned}$$

(62)

Consider next the penguin operators of Eqs. (102)–(104), which match at one loop to the dipole. The bound on the coefficient at $M \simeq 100 m_t$ is $C^{e \mu }_{HE} \lesssim 0.1$, so I neglect mixing into these operators, and approximate

$$\begin{aligned} C^{e \mu }_{HE} (m_W)= & {} C^{e \mu }_{HE}(M), \nonumber \\ C^{e \mu }_{HL(1)} (m_W)= & {} C^{e \mu }_{HL(1)} (M),\\ C^{e \mu }_{HL(3)} (m_W)= & {} C^{e \mu }_{HL(3)} (M). \nonumber \end{aligned}$$

(63)

In running from $M \rightarrow m_W$, the RGEs given in [39, 40, 43] show that gauge interactions will renormalise the photon dipole coefficient $C_{e\gamma }^{\mu e *}$, and cause it to receive contributions from $C_{e Z}^{\mu e *}$, $C^{\mu e cc *}_{LEQU(1)}$, $C^{\mu e cc *}_{LEQU(3)}$, $C^{\mu e tt *}_{LEQU(1)}$, and $C^{\mu e tt*}_{LEQU(3)}$. This gauge mixing of scalars to tensors to dipoles is analogous to the QED mixing below $m_W$. In addition, as given in [39, 40], Higgs loops will mix vector four-fermion operators into scalars and tensors. In the following, the third order vector$\rightarrow$scalar$\rightarrow$tensor$\rightarrow$dipole mixing is neglected, and only the vector$\rightarrow$tensor$\rightarrow$dipole is retained for vector and tensor operators with a top bilinear. Defining a coefficient vector

$$\begin{aligned} \vec {C}= & {} \left( C_{EU}^{\mu e tt*}, C_{EQ}^{\mu e tt*}, C^{\mu e tt*}_{LEQU(1)},\;C^{\mu e cc*}_{LEQU(1)}, C^{\mu e tt *}_{LEQU(3)}, \right. \nonumber \\&\left. C^{\mu e cc *}_{LEQU(3)}, C_{e\gamma }^{\mu e *}, C_{eZ}^{\mu e *}\right) , \end{aligned}$$

then, from [39, 40, 43], the electroweak anomalous dimension matrix ${\varvec{\gamma }}_{\gamma t}$ such that $\mu \partial \vec {C}/\partial \mu = \frac{\alpha _{em}}{4\pi } \vec {C} {\varvec{\gamma }}$ is approximately

$$\begin{aligned} {\varvec{\gamma }}_{\gamma t} \!\sim \!\left[ \! \begin{array}{cccccccc} 0&{}0&{}0&{}0&{}-\frac{ Y_t Y_\mu }{2e^2}&{}0&{}0&{}0\\ ~0~&{}~0~&{}0&{}0&{}-\frac{ Y_t Y_\mu }{2e^2}&{}0&{}0&{}0\\ 0&{}0&{}-5+ \frac{15 Y_t^2}{2e^2} &{}0&{} \frac{7}{3} &{}0 &{}0 &{}0\\ 0&{}0&{}0&{}-5+ \frac{15 Y_c^2}{2e^2} &{}0&{} \frac{7}{3} &{}0 &{}0 \\ 0&{}0&{} 112 &{}0&{} 8.5 + \frac{3Y_t^2}{2e^2}&{}0&{}\frac{16Y_t}{eY_\mu } &{}\frac{8 Y_t}{\sqrt{3}e Y_\mu }\\ 0&{}0&{}0&{}112&{}0 &{} 8.5 + \frac{3Y_c^2}{2e^2}&{}\frac{16Y_c}{eY_\mu } &{}\frac{8 Y_c}{\sqrt{3}eY_\mu }\\ 0&{}0&{}0 &{}0&{}\frac{7Y_tY_\mu }{e}&{}\frac{7Y_cY_\mu }{e}&{} 7 +\frac{3Y_t^2}{e^2} &{} -\frac{24}{\sqrt{3}}\\ 0&{}0&{}0&{}0&{}\frac{22Y_tY_\mu }{6 e}&{} \frac{22Y_cY_\mu }{6 e}&{} \frac{12}{\sqrt{3}} &{}-\frac{8}{3}+ \frac{3Y_t^2}{e^2}\\ \end{array} \!\right] \nonumber \\ \end{aligned}$$

(64)

where small Yukawa couplings and fractions were neglected, $\sin ^2\theta _W = 1/4$, and renormalisation and mixing to the vectors was neglected because they only affect the dipole at $\mathcal{O}(\alpha ^2 \log ^2)$. The RGE for the tensor coefficient $C^{e \mu tt }_{LEQU(3)}$, which mixes to the “right-handed” dipole $C_{e\gamma }^{e \mu }$ would instead include the vector contribution:

$$\begin{aligned} \mu \frac{\partial }{\partial \mu } C_{LEQU(3)}^{ e \mu tt}= & {} \cdots - \frac{\alpha _{em}}{4\pi } \frac{Y_tY_\mu }{2e^2} \nonumber \\&\times \left( C_{LU}^{\mu e tt} +C_{LQ(1)}^{\mu e tt}- 3C_{LQ(3)}^{\mu e tt}\right) , \end{aligned}$$

(65)

rather than the first two rows of Eq.(64). The approximate solution of these RGEs, if the running of gauge and Yukawa couplings is neglected,⁵ is

$$\begin{aligned} C_{B}(m_W)\simeq & {} C_{A}(M) \left( \delta _{A,B} - \frac{\alpha _{em} }{4\pi } \left[ \gamma _{\gamma t}\right] _{A,B} \ln \frac{M}{m_W} \right. \nonumber \\&\left. + \frac{\alpha _{em} ^2 }{32\pi ^2} \left[ \gamma _{\gamma t} \gamma _{\gamma t}\right] _{A,B} \ln ^2 \frac{M}{m_W} +\cdots \right) . \end{aligned}$$

(66)

Table 1 Approximate “one-operator-at-a-time” constraints on operator coefficients evaluated at the scale M, from the MEG bound [61] on $BR(\mu \rightarrow e \gamma )$, as given in Eqs. (67), (68). For a given choice of scale M, the quantity in either left column should be less than the number in the right colomn multiplied by ${M^2}/{m_t^2}$. The operators are labelled in the same way as the coefficients, and given in Appendix D

Allowing the index B of Eq. (66) to run over the coefficients present on the right side of Eq. (59), the anomalous dimension matrix of Eq. (64) and the bound (53) give

$$\begin{aligned}&1.2 \times 10^{-8}\frac{M^2}{m_t^2} \gtrsim C^{\mu e *}_{e \gamma }(M) - 0.016 C^{\mu e *}_{EH}(M) \nonumber \\&\quad + 0.001 C^{e \mu }_{HE} (M) -0.0043C^{\mu e *}_{e Z}(M) \ln \frac{M}{m_W} \nonumber \\- & {} 59 C^{\mu e tt*}_{LEQU(3)}(M) \ln \frac{M}{m_W} \nonumber \\- & {} C^{\mu e cc*}_{LEQU(3)}(M) \left( 0.43 \ln \frac{M}{m_W} + 1.5\right) \nonumber \\+ & {} 0.039 C^{\mu e tt*}_{LEQU(1)}(M) \ln ^2 \frac{M}{m_W} \nonumber \\+ & {} 0.002 \left( 1 + \ln \frac{M}{m_W} \right) C^{\mu e cc*}_{LEQU(1)}(M) \nonumber \\- & {} 4.8 \times 10^{-5} \ln ^2 \frac{M}{m_W} {\Big (} C_{EQ}^{\mu e tt *}(M) +C_{EU}^{\mu e tt *}(M) {\Big )} \end{aligned}$$

(67)

(where $m_t$ is written instead of the Higgs vev, to avoid $\sqrt{2}$ issues). This constraint, as well as the equivalent bound on $C_{e\gamma }^{e \mu }(m_\tau )$:

$$\begin{aligned} 1.2\times & {} 10^{-8}\frac{M^2}{m_t^2} \gtrsim C^{e \mu }_{e \gamma }(M) -0.016 C^{e \mu }_{EH}(M) \nonumber \\+ & {} 0.001 {\Big (} C^{e \mu }_{HL(1)} (M) +C^{e \mu }_{HL(3)} (M) {\Big )}\nonumber \\- & {} 0.0043C^{e\mu }_{e Z}(M) \ln \frac{M}{m_W} \nonumber \\- & {} 59 C^{e \mu tt}_{LEQU(3)}(M) \ln \frac{M}{m_W} \nonumber \\- & {} C^{e\mu cc}_{LEQU(3)}(M) \left( 0.43 \ln \frac{M}{m_W} + 1.5\right) \nonumber \\+ & {} 0.039 C^{e \mu tt}_{LEQU(1)}(M) \ln ^2 \frac{M}{m_W} \nonumber \\+ & {} 0.002 \left( 1 + \ln \frac{M}{m_W} \right) C^{e \mu cc}_{LEQU(1)}(M) \nonumber \\- & {} 4.8 \times 10^{-5} \ln ^2 \frac{M}{m_W} \nonumber \\\times & {} {\Big (} C_{LU}^{e \mu tt }(M) +C_{LQ(1)}^{e \mu tt }(M)-3C_{LQ(3)}^{e \mu tt }(M) {\Big )} \end{aligned}$$

(68)

gives the “one-operator-at-a-time” bounds listed in Table 1. These bounds are obtained by assuming that one operator dominates the $\mu \rightarrow e \gamma$ amplitude, so neglect interferences between the various coefficients. If both the left-handed dipole $C_{e\gamma }^{ \mu e*}$ and the right-handed $C_{e\gamma }^{e \mu }$ are generated, then the right column could be divided by $\sqrt{2}$. The bounds of the first six rows agree to within a factor 2 with the constraints given in [43], who do not constrain the coefficients given in the last four rows. The vector operators, given in the last two rows, barely pass the “constrainable” threshhold defined above ($C <1$ at $M = 100~m_t$). This retroactively justifies that the mixing of vectors into scalars was neglected, because it would be suppressed by an additional loop.

6 Discussion of the machinery and its application to $\mu \rightarrow e \gamma$

The MEG experiment [61] sets a stringent bound on the dipole operator coefficients at low energy (see Eq. (53)). In translating this constraint to a scale $M> m_W$, the analysis here aimed to include the “Leading Order” contribution of all “constrainable” operators, where LO was taken to mean numerically largest, and an operator was deemed constrainable if a bound $C<1$ could be obtained at $M\ge 100 m_t$. However, two-loop running, which gives the leading order mixing of vectors to the dipole, is not included here, so many constraints on vector operators are missing. As a result, the one-operator-at-a-time limits given in Table 1 are obtained from a combination of tree, one- and two-loop matching, with RGEs at one loop. Why do these multi-loop matching contributions arise?

First consider operator dimensions above and below $m_W$. There is a rule of thumb in EFT [47]: that one matches at a loop order lower than one runs, where the loops are counted in the interaction giving the running. This makes sense if the loop expansion is in one coupling, or if the same diagram gives the running and one-loop matching, because the running contribution is relatively enhanced by the log. For instance, an electroweak box diagram at $m_W$ generates a four-fermion operator “at tree level” in QCD, which can run down with one-loop QCD RGEs. One could hope that a similar argument might apply above $m_W$: a diagram giving one-loop matching could contribute to running above $m_W$, so the subdominant matching could be neglected. However, this is not the case at $m_W$, because SU(2)-invariant dimension-six operators from above $m_W$ can match onto operators that would-be dimension eight if one imposed SU(2), but that are $\mathcal{O}(1/M^2)$ and dimension six in the QED$\times$QCD-invariant theory below $m_W$. For example, the LFV Z penguin operators given in Eqs. (102)–(104) match at one loop onto the “dimension-eight” dipole $y_\mu H^\dagger H(\overline{L}_e H \sigma \cdot F E_\mu )$. Similarly, the LFV Higgs interaction $H^\dagger H(\overline{L}_e H E_\mu )$ matches at two loops to the same “would-be dimension-eight” dipole. So the expectation that running dominates matching can fail at $m_W$.

The expectation that one loop is larger than two loops can fail when perturbing in a hierarchy of Yukawa couplings. The dipole’s affinity to Yukawas arises because the lepton chirality changes, and the operator has a Higgs leg. The dipole operator here is defined to include a muon Yukawa coupling $Y_\mu$ (see Eq. (51)), because in many models, the Higgs leg attaches to a Standard Model fermion, and/or the lepton chirality flips due to a Higgs coupling. And while it is difficult to avoid the $Y_\mu$ in one-loop contributions to the dipole (see the discussion in [63]), there are more possibilities at two loops. In particular, it is “well known” [65] that the leading contribution to $\mu \rightarrow e \gamma$ of a flavour-changing Higgs interaction, is via the two-loop top and W diagrams included in the matching contribution of Eq. (60).

Its unclear to the author what to do about either of these problems. Perhaps only the LFV operators with at least two Higgs legs give their leading contributions in matching rather than running.⁶ Maybe performing the matching and running at two loops would include the leading contributions in loops, logs, and Yukawa hierarchies. However, a complete two-loop analysis would take some effort – perhaps it would be simpler to list all the possible operators at the scale M, locate their “Leading Order” contributions, and include them.

As discussed above, it is important to match with care at $m_W$. A slightly different question is whether it is important to match onto the extended (non-SU(2)-invariant) operator basis at $m_W$? The answer probably depends on the low energy observables of interest. In the analysis here of $\mu \rightarrow e \gamma$, the four-fermion operators that were added below $m_W$ (such as the scalar four-fermion operators $\mathcal{O}^{e\mu bb}_{S,YY}$, $\mathcal{O}^{e\mu \tau \tau }_{S,YY}$ and $\mathcal{O}^{e\mu \mu \mu }_{S,YY}$ given in Eq. (2)), are numerically irrelevant provided that the matching is performed at two loops. This is because they were generated in tree matching by the Higgs LFV operator $H^\dagger H(\overline{L} H E)$, suppressed by the $b,\tau$ or $\mu$ Yukawa coupling; see Eqs. (23), (26), (39) and (41). Then, in QED running, they mix to the dipole (possibly via the tensor), which brings in another factor of the light fermion mass. With tree matching, this is the best constraint on the Higgs LFV operator, so is interesting to include. However, it is irrelevant compared with the two-loop diagrams involving a top and W loop, which match the Higgs LFV operator directly onto the dipole. This two-loop matching contribution is relatively enhanced by a factor ${\sim }100$ as can be seen by comparing the square brackets of Eqs. (59) and (60). So in the case of $\mu \rightarrow e \gamma$, it seems that one would get the correct constraints on operator coefficients at M by using an SU(2)-invariant four-fermion operator basis all the way between $m_\mu$ and M, provided the matching at $m_W$ is performed to whatever loop order retains the “leading” contributions.

The QED mixing between $m_\mu$ and $m_W$ modifies significantly the combination of operators that are constrained by $\mu \rightarrow e \gamma$. This is illustrated in Fig. 2, which shows that the constraint has rotated in operator space, to constrain the linear combination of coefficients given in Eq. (58). Coefficients of tensor operators that were of a similiar magnitude to the dipole coefficient could give significant enhancement or cancellations. So the QED running is important. In addition, the MEG constraint on $BR(\mu \rightarrow e \gamma )$ is restrictive – as discussed in Sect. 5.1, it could constrain New Physics which contributes at one loop up to a scale $M \sim 10^7$ GeV. So it would be sensitive to two-loop contributions from LFV operators at a scale of $10^5$ GeV. However, in matching at $m_W$ onto SU(2)-invariant dimension-six operators, many of the tensor and scalar operators which mix with the dipole below $m_W$, are generated with small coefficients which give a negligeable contribution to $\mu \rightarrow e \gamma$. The point is that the scalars and tensors involving leptons and d-type quarks are generated by the Higgs LFV operator, whose leading contribution to $\mu \rightarrow e \gamma$ arises in two-loop matching.

There are many improvements that could be made to these estimates. Including the experimental constraints from $\mu \rightarrow e \bar{e} e$ and $\mu \rightarrow e ~\mathrm{conversion}$ would directly constrain the vector operators, and give independent constraints on some of the operators that contribute to $\mu \rightarrow e \gamma$. There are more operators than constraints, so this could allow one to identify linear combinations of operators that are not constrained. One-loop matching is motivated by the restrictive experimental bounds, which allow one to probe multi-loop effects. In addition, there are operators which require one-loop matching, such as the two-gluon operators relevant to $\mu \rightarrow e ~\mathrm{conversion}$. Two-loop running is required to get the leading order contribution of vector operators to $\mu \rightarrow e \gamma$, and could be interesting above $m_W$ if there are diagrams that dominate the one-loop running due to the presence of large Yukawas, or if quark flavour-off-diagonal operators are included, which may contribute to $\mu \rightarrow e \gamma$ at two loops [64]. It is also motivated by the experimental sensitivity. Finally, dimension-eight operators can be relevant if the New Physics scale is not to high [64].

7 Summary

This paper assumes that there is new lepton-flavour violating (LFV) physics at a scale $M \gg m_W$, and no relevant other new physics below. So at scales below M, LFV can be described in an Effective Field Theory constructed with Standard Model fields and dimension-six operators. The aim was to translate experimental constraints on selected $\mu \leftrightarrow e$ flavour changing processes, from the low energy scale of the experiments to operator coefficients at the scale M. As a first step, this paper reviews and compiles some of the formalism required to get from low energy to the weak scale: a QED$\times$QCD-invariant operator basis is given in Sect. 2, the one-loop RGEs to run the coefficients to $m_W$ are discussed in Sect. 3, the anomalous dimensions mixing scalars, tensors and dipoles are given in Appendix A, and tree matching onto SU(2)-invariant operators at $m_W$ is presented in Sect. 4.

As a simple application of the formalism, the experimental bounds on $\mu \rightarrow e \gamma$ were translated to the scale M in Sect. 5. The process $\mu \rightarrow e \gamma$ was chosen because it is an electromagnetic decay, and it constrains only the coefficients of the two dipole operators. The resulting constraints at M on two linear combinations of operators are given in Eqs. (67) and (68). These limits are approximative, due to the many simplifications discussed in the paper, valid at best to one significant figure. Bounds on individual operators can be obtained by assuming one operator dominates the sum; the resulting constraints are listed in Table 1. At a scale $M\sim 100 m_t$, $\mu \rightarrow e \gamma$ is sensitive to over a dozen operators, whereas, if $M \gtrsim 10^{7}$ GeV, then $\mu \rightarrow e \gamma$ is sensitive to only a few.

The formalism of the first sections did not work well for $\mu \rightarrow e \gamma$. Tree matching and one-loop running missed the largest contributions of some operators, as discussed in Sect. 6. This curious problem could benefit from more study, in order to identify a practical and systematic solution.

Appendices

Appendix A: Operator normalisation

All the operators introduced Sect. 2 appear in the Lagrangian with a coefficient $-C/M^2$, and the operator normalisation is chosen to ensure that the Feynman rule is $-i C/M^2$. This implies a judicious distribution of $\frac{1}{2}$s, which is the subject of this Appendix.

The $\mathcal{O}^{e \mu }$ are flavour-changing, so can be imagined as off-diagonal elements of the matrix $\mathcal{O}$ in lepton-flavour space. They annihilate a $\mu$, and create an e, so the hermitian conjugate of the operator should appear in the Lagrangian too. However, the Lagrangian is a flavour-scalar, so in the Lagrangian is -$\frac{1}{M^2}$Tr$[ C \mathcal{O}]$, where the coefficients C are also a matrix in flavour space. (For instance, to obtain only $\mathcal{O}^{e \mu }$ in the Lagrangian, one takes only $C^{e \mu } \ne 0$.) Adding $+h.c.$ means adding -$\frac{1}{M^2}$Tr$[ \mathcal{O}^\dagger C^\dagger ]$. If $\mathcal{O}^\dagger = \mathcal{O}$, as in the case of vector operators, then there are two possibilities for the matrix-in-flavour-space C: either take $C^\dagger = C$ (so if $C^{e \mu } \ne 0$, then $C^{ \mu e }= C^{e \mu *}$), so Tr$[ \mathcal{O}^\dagger C^\dagger ] =$ Tr$[ C \mathcal{O}]$. Then in the Lagrangian appears Tr$[ \mathcal{O}^\dagger C^\dagger ] +$ Tr$[ C \mathcal{O}]$, so the operator should be normalised with 1/2 to compensate for this double-counting, and thereby ensure that the F-rule is $-i C^{e \mu }/M^2$. Alternatively, one does not impose $C^\dagger = C$, and only puts the desired $C^{e \mu } \ne 0$ coupling in the Lagrangian, where the $+h.c.$ generates the anti-particle amplitude, and the Feynman rule is again $-i C^{e \mu }/M^2$, without the factor of 1/2 in the operator definition. Scalars and tensor operators are not hermitian, e.g.:

$$\begin{aligned}{}[S] = \left[ \begin{array}{ll} \overline{e} P_Y e &{} \overline{e} P_Y \mu \\ \overline{\mu } P_Y e &{} \overline{\mu } P_Y \mu \\ \end{array} \right] ,\ [S]^\dagger = \left[ \begin{array}{ll} \overline{e} P_X e &{} \overline{e} P_X \mu \\ \overline{\mu } P_X e &{} \overline{\mu } P_X \mu \\ \end{array} \right] ,\ X \ne Y, \end{aligned}$$

so a scalar or tensor operator $\mathcal{O}^{e\mu }$ will induce two distinct $\mu \rightarrow e$ flavour-changing interactions of different chirality. In the case of the dipole, $[\mathcal{O}_{D,R }]^\dagger =[\mathcal{O}_{D,L }]$, so if one writes

$$\begin{aligned}&- \frac{C^{e\mu }_{D,R } }{M^2}\mathcal{O}^{e\mu }_{D,R } - \frac{C^{\mu e}_{D,R } }{M^2}\mathcal{O}^{\mu e}_{D,R } - \frac{ C^{e\mu }_{D,L } }{M^2}\mathcal{O}^{e\mu }_{D,L } \nonumber \\&\quad - \frac{ C^{\mu e}_{D,L } }{M^2}\mathcal{O}^{\mu e}_{D,L } + h.c. \end{aligned}$$

(69)

Then the $+h.c.$ is double-counting, it just adds all the same operators a second time (which implies $C^{e\mu *}_{D,L } = C^{\mu e}_{D,R }$, $C^{e\mu *}_{D,R } = C^{\mu e}_{D,L }$). So I include in $\mathcal {L}$ the first and third operaters of Eq. (69), and the +h.c..

Appendix B: Anomalous dimension matrix in QED

In this appendix are given the various submatrices of the anomalous dimension matrix ${\varvec{\Gamma }}_{STD}$ of Eq. (15). The relevant diagrams are given in Fig. 1.

• 1. For scalar operators, the penguin diagrams (first and second) do not contribute to one-loop mixing among four-fermion operators, because the photon couples to the vector current. However, the second penguin diagram, with on-shell photon (no fermions) mixes the $\mathcal{O}^{e\mu ll}_{S,YY}$ operators for $l \in \{e,\mu \}$, to the dipole. This gives the matrix

  $$\begin{aligned} \gamma _{S,D}^{l,} = \begin{array}{c|cc} &{}C_{D,L}^{e \mu } &{} C_{D,R}^{e \mu }\\ \hline C_{S,LL}^{e \mu ll}&{} -\frac{m_l }{e m_\mu } &{}0\\ C_{S,RR}^{e \mu ll}&{}0&{} -\frac{m_l }{e m_\mu } \\ \end{array} \end{aligned}$$

  (70)

  Diagrams 3 and 4 are the same as the mass renormalisation diagrams ($\gamma _m = 6$ in QED), so combined with the wave-function diagrams, they renormalise scalar operators, giving a diagonal matrix:

  $$\begin{aligned} \gamma _{S,S}^{f_1,f_2} = \begin{array}{c|cccc} &{}C_{S,LL}^{e \mu f f} &{} C_{S, RR}^{e \mu f f}&{} C_{S,LR}^{e \mu f f} &{} C_{S,RL}^{e \mu f f}\\ \hline C_{S,LL}^{e \mu f f}&{} 6(1 + Q_f^2) &{}0&{} 0 &{}0\\ C_{S,RR}^{e \mu f f}&{}0&{} 6(1 + Q_f^2) &{}0&{} 0\\ C_{S,LR}^{e \mu f f}&{}0&{} 0&{} 6(1 + Q_f^2) &{}0\\ C_{S,RL}^{e \mu f f}&{}0&{}0&{}0&{} 6(1 + Q_f^2) \\ \end{array}\nonumber \\ \end{aligned}$$

  (71)

  where the $(1 + Q_f^2)$ arises from the photon exchange across either current. The last four diagrams mix the YY scalars to the tensors (the YX tensor vanishes) with $\gamma = 2Q_f$:

  $$\begin{aligned} \gamma _{S,T}^{f,f} = \begin{array}{c|cc} &{}C_{T,LL}^{e \mu f f} &{} C_{T, RR}^{e \mu f f} \\ \hline C_{S,LL}^{e \mu f f}&{} 2 Q_f &{}0 \\ C_{S,RR}^{e \mu f f}&{}0&{} 2Q_f \\ C_{S,LR}^{e \mu f f}&{}0&{} 0 \\ C_{S,RL}^{e \mu f f}&{}0&{}0\\ \end{array} \end{aligned}$$

  (72)

• 2. The tensors mix to the dipoles, via the first diagram with the $f_2$ line removed. This gives

  $$\begin{aligned} \gamma _{T,D}^{f,~} = \begin{array}{c|cc} &{}C^{D,L}_{f} &{} C^{D, R}_{f} \\ \hline C^{T,LL}_{f}&{} 8 \frac{Q_fN_c m_f}{m_\mu e} &{}0 \\ C^{T,RR}_{f}&{}0&{} 8 \frac{Q_fN_c m_f}{m_\mu e} \\ \end{array} \end{aligned}$$

  (73)

  The third and fourth diagrams do not renormalise the tensors because $\gamma ^\alpha \sigma \gamma _\alpha = 0$, but the wave-function diagrams do:

  $$\begin{aligned} \gamma _{T,T}^{f,f} = \begin{array}{c|cc} &{}C_{T,LL}^{e \mu f f} &{} C_{T, RR}^{e \mu f f} \\ \hline C_{T,LL}^{e \mu f f}&{} -2(1 + Q_f^2) &{}0 \\ C_{T,RR}^{e \mu f f}&{}0&{}- 2(1 + Q_f^2) \\ \end{array} \end{aligned}$$

  (74)

  and finally, the last four diagrams mix the tensors to scalars, giving

  $$\begin{aligned} \gamma _{T,S}^{f,f} = \begin{array}{c|cc} &{}C_{S,LL}^{e \mu f f} &{} C_{S, RR}^{e \mu f f} \\ \hline C_{T,LL}^{e \mu f f}&{} -96 Q_f &{}0 \\ C_{T,RR}^{e \mu f f}&{}0&{} -96 Q_f \\ \end{array} \end{aligned}$$

  (75)

  These tensor$\rightarrow$scalar mixing elements of the QED anomalous dimension matrix are large, suggesting that one could redefine the operator basis to use a linear combination of scalar and tensor operators with smaller off-diagonal elements. However, QCD does not mix the scalars and tensors, which favours them as basis operators. In addition, the tensor$\rightarrow$scalar mixing does not enter the $\mu \rightarrow e \gamma$ example of Sect. 5, where the scalar–tensor operator basis gives the correct behaviour, as verified by comparing EFT and exact calculations of $\mu \rightarrow e \gamma$ in the 2HDM [64]. The dipole also renormalies itself [19], although this effect is not included here:

  $$\begin{aligned} \gamma _{_{D,D}} = \left[ \begin{array}{cc} 16 &{}\quad 0\\ 0 &{}\quad 16 \end{array}\right] . \end{aligned}$$

• 3. The diboson operators $\mathcal{O}_{GG,Y},\mathcal{O}_{FF,Y}$ are of dimension seven, so the four-fermion operators and dipole operators do not mix into them.

Appendix C: Spinor stuff

The Fierz identities can be written for chiral fermions as

$$\begin{aligned} (\overline{a} P_L b)(\overline{c} P_R d)= & {} -\frac{1}{2}(\overline{a} \gamma ^{\mu } P_R d) (\overline{c} \gamma _{\mu } P_L b), \end{aligned}$$

(76)

$$\begin{aligned} (\overline{a} \gamma ^{\mu } P_{L,R} b)(\overline{c} \gamma _{\mu } P_{L,R} d)= & {} (\overline{a} \gamma ^{\mu } P_{L,R} d)(\overline{c} \gamma _{\mu } P_{L,R} b), \end{aligned}$$

(77)

$$\begin{aligned} (\overline{a} P_X b)(\overline{c} P_Xd)= & {} -\frac{1}{2}(\overline{a} P_X d)(\overline{c} P_X b) \nonumber \\&-\frac{1}{8}(\overline{a} \sigma ^{\nu \mu } P_X d) (\overline{c} \sigma _{\nu \mu } P_X b), \nonumber \\ \end{aligned}$$

(78)

$$\begin{aligned} (\overline{a} \sigma ^{\nu \mu } P_{X} b)(\overline{c} \sigma _{\nu \mu } P_{X} d)= & {} \frac{1}{2} (\overline{a} \sigma ^{\nu \mu } P_{X} d)(\overline{c} \sigma _{\nu \mu } P_{X} b) \nonumber \\&-6(\overline{a} P_X d)(\overline{c} P_X b) \end{aligned}$$

(79)

where the relation $\sigma _{\mu \nu } = \frac{i}{2} \varepsilon _{\mu \nu \alpha \beta } \sigma ^{\alpha \beta } \gamma _5$ was used to replace $\sigma$ with $\sigma P_X$. It implies that $(\overline{e}\sigma ^{\alpha \beta } \gamma _5 \mu ) (\overline{\psi }\sigma _{\alpha \beta } \gamma _5 \chi ) = (\overline{e} \sigma _{\mu \nu } \mu ) (\overline{\psi }\sigma ^{\mu \nu } \chi )$, so

$$\begin{aligned}&(\overline{e}\sigma ^{\alpha \beta } P_Y \mu ) (\overline{\psi }\sigma _{\alpha \beta } P_Y \chi ) = \frac{1}{2} (\overline{e}\sigma ^{\alpha \beta } \mu ) (\overline{\psi }\sigma _{\alpha \beta } \chi ), \nonumber \\&(\overline{e}\sigma ^{\alpha \beta } P_Y \mu ) (\overline{\psi }\sigma _{\alpha \beta } P_X \chi ) =0 ~~~(X\ne Y). \end{aligned}$$

(80)

Appendix D: SU(2)-invariant dimension-six operators

This appendix lists dimension-six, SM-gauge-invariant operators involving e–$\mu$ flavour change. The operators are in the Buchmuller–Wyler basis, as pruned in Grzadkowski et al. [38], and this list is referred to as the BWP basis. The operators are assumed to be added to the Lagrangian $+ h.c.$; when this gives the $\bar{\mu } e$ operator, it is not listed. The $\tau ^a$ are the Pauli matrices, with

$$\begin{aligned} \tau ^2 = \left[ \begin{array}{cc} 0 &{}-i\\ i &{} 0 \end{array}\right] . \end{aligned}$$

The four-fermion operators involving e–$\mu$ flavour change and two quarks are

$$\begin{aligned} \mathcal{O}_{L Q}^{(1) e \mu nm}= & {} \frac{1}{2}(\overline{L}_e \gamma ^\alpha L_\mu ) (\overline{Q}_n \gamma ^\alpha Q_m ) \nonumber \\= & {} \frac{1}{2}[(\overline{e}_e \gamma ^\alpha P_L \mu ) +(\overline{\nu }_e \gamma ^\alpha P_L \nu _\mu )]\nonumber \\&\times [(\overline{u}_n \gamma ^\alpha P_L u_m ) + (\overline{d}_n \gamma ^\alpha P_L d_m )], \end{aligned}$$

(81)

$$\begin{aligned} \mathcal{O}_{L Q}^{(3)e \mu nm}= & {} \frac{1}{2}(\overline{L}_e \gamma ^\alpha \tau ^aL_\mu ) (\overline{Q}_n \gamma ^\alpha \tau ^a Q_m )\nonumber \\= & {} (\overline{\nu }_e \gamma ^\alpha P_L \mu ) (\overline{d}_n \gamma ^\alpha P_L u_m) \nonumber \\&+ (\overline{e}_e \gamma ^\alpha P_L \nu _\mu )(\overline{u}_n \gamma ^\alpha P_L d_m ) \nonumber \\&+ \frac{1}{2}[(\overline{\nu }_e \gamma ^\alpha P_L \nu _\mu ) - (\overline{e}_e \gamma ^\alpha P_L \mu )]\nonumber \\&\times [(\overline{u}_n \gamma ^\alpha P_L u_m ) - (\overline{d}_n \gamma ^\alpha P_L d_m )], \end{aligned}$$

(82)

$$\begin{aligned}&\mathcal{O}^{e \mu nm}_{EQ} = \frac{1}{2}(\overline{E}_e \gamma ^\alpha E_\mu ) (\overline{Q}_n \gamma ^\alpha Q_m ),\end{aligned}$$

(83)

$$\begin{aligned}&\mathcal{O}^{e \mu nm}_{LU} = \frac{1}{2} (\overline{L}_e \gamma ^\alpha L_\mu ) (\overline{U}_n \gamma ^\alpha U_m ),\end{aligned}$$

(84)

$$\begin{aligned}&\mathcal{O}^{e \mu nm}_{LD} = \frac{1}{2} (\overline{L}_e \gamma ^\alpha L_\mu ) (\overline{D}_n \gamma ^\alpha D_m ),\end{aligned}$$

(85)

$$\begin{aligned}&\mathcal{O}^{e \mu nm}_{EU} = \frac{1}{2} (\overline{E}_e \gamma ^\alpha E_\mu ) (\overline{U}_n \gamma ^\alpha U_m ),\end{aligned}$$

(86)

$$\begin{aligned}&\mathcal{O}^{e \mu nm}_{ED} = \frac{1}{2} (\overline{E}_e \gamma ^\alpha E_\mu ) (\overline{D}_n \gamma ^\alpha D_m ), \end{aligned}$$

(87)

$$\begin{aligned} \mathcal{O}^{e \mu nm}_{LE Q U}= & {} \left( \overline{L}_e^A E_\mu \right) \epsilon _{AB} \left( \overline{Q}^B_n U_m \right) \nonumber \\= & {} -(\overline{\nu }_e P_R \mu ) (\overline{d}_n P_R u_m ) + (\overline{e}_e P_R \mu ) (\overline{u}_nP_R u_m ),\nonumber \\ \end{aligned}$$

(88)

$$\begin{aligned} \mathcal{O}^{ \mu e nm}_{LE Q U}= & {} \left( \overline{L}_\mu ^A E_e \right) \epsilon _{AB} \left( \overline{Q}^B_n U_m\right) ,\end{aligned}$$

(89)

$$\begin{aligned} \mathcal{O}^{e \mu nm}_{LE D Q}= & {} (\overline{L}_e E_\mu ) (\overline{D}_n Q_m ) \nonumber \\= & {} (\overline{\nu }_e P_R \mu ) (\overline{d}_n P_L u_m ) + (\overline{e}_e P_R \mu ) (\overline{d}_nP_L d_m ), \end{aligned}$$

(90)

$$\begin{aligned} \mathcal{O}^{\mu e nm}_{LE DQ }= & {} (\overline{L}_\mu E_e ) (\overline{D}_n Q_m ), \end{aligned}$$

(91)

$$\begin{aligned} \mathcal{O}^{e \mu nm}_{T, LEQU}= & {} \left( \overline{L}_e^A \sigma ^{\mu \nu } E_\mu \right) \epsilon _{AB} \left( \overline{Q}^B_n \sigma _{\mu \nu } U_m\right) , \end{aligned}$$

(92)

$$\begin{aligned} \mathcal{O}^{\mu e nm}_{T, LEQU}= & {} \left( \overline{L}_\mu ^A \sigma ^{\mu \nu } E_e \right) \epsilon _{AB} \left( \overline{Q}^B_n \sigma _{\mu \nu } U_m\right) , \end{aligned}$$

(93)

where L, Q are doublets and E, U are singlets (lower case are Dirac spinors, SU(2) components selected with $P_{L,R}$), n, m are possibly equal quark family indices, and A, B are SU(2) indices. The doublet quarks are in the d, s, b mass eigenstate basis. The operator names are as in [38] with $\phi \rightarrow H$; the flavour indices are in superscript.

The operators involving e–$\mu$ flavour change, and leptons, are

$$\begin{aligned} \mathcal{O}^{e \mu ii}_{L L}= & {} \frac{1}{2}(\overline{L}_e \gamma ^\alpha L_\mu ) (\overline{L}_i \gamma ^\alpha L_i ) \nonumber \\= & {} \frac{1}{2}[(\overline{e}_e \gamma ^\alpha P_L \mu ) + (\overline{\nu }_e \gamma ^\alpha P_L \nu _\mu )]\nonumber \\&+ [(\overline{\nu }_i \gamma ^\alpha \tau ^a P_L \nu _i ) (\overline{e}_i \gamma ^\alpha \tau ^a P_L e_i )] , \end{aligned}$$

(94)

$$\begin{aligned} \mathcal{O}^{e \mu ii}_{L E}= & {} \frac{1}{2}(\overline{L}_e \gamma ^\alpha L_\mu ) (\overline{E}_i \gamma ^\alpha E_i ), \end{aligned}$$

(95)

$$\begin{aligned} \mathcal{O}^{ii e \mu }_{ LE }= & {} \frac{1}{2} (\overline{L}_i \gamma ^\alpha L_i ) (\overline{E}_e \gamma ^\alpha E_\mu ), \end{aligned}$$

(96)

$$\begin{aligned} \mathcal{O}^{e \mu ii}_{EE}= & {} \frac{1}{2}(\overline{E}_e\gamma ^\alpha E_\mu ) (\overline{E}_i \gamma ^\alpha E_i ),\end{aligned}$$

(97)

$$\begin{aligned} -\frac{1}{2}\mathcal{O}^{e \tau \tau \mu }_{LE }= & {} (\overline{L}_e E_\mu ) (\overline{E}_\tau L_\tau ), -\frac{1}{2}\mathcal{O}^{\mu \tau \tau e}_{LE }= (\overline{L}_\mu E_e ) (\overline{E}_\tau L_\tau ) \nonumber \\= & {} (\overline{\nu }_e P_R \mu ) (\overline{\tau } P_L \nu _\tau ) + (\overline{e}_e P_R \mu ) (\overline{\tau } P_L \tau ), \end{aligned}$$

(98)

where i is now a charged lepton family index, and hermitian operators are defined with a factor 1/2, to agree with the factor of 1/2 present below $m_W$ as discussed in Sect. A.

The operator (98) appears in the BWP basis in its Fierz-transformed version, corresponding to the operator name given above. Since here the e–$\mu$ flavour change below $m_W$ remains inside a spinor contraction, the versions are used interchangeably.

Then there are the operators allowing interactions with gauge bosons and Higgses. This includes the dipoles, which are normalised with the muon Yukawa coupling so as to match onto the normalisation of Kuno–Okada [1]:

$$\begin{aligned} \mathcal{O}^{e \mu }_{EH }= & {} H^\dagger H \overline{L}_e H E_\mu \mathcal{O}^{\mu e}_{E H } = H^\dagger H \overline{L}_\mu H E_e , \end{aligned}$$

(99)

$$\begin{aligned} \mathcal{O}^{e \mu }_{eW }= & {} y_\mu (\overline{L}_e \vec {\tau }^a H \sigma ^{\alpha \beta } E_\mu ) W^a_{\alpha \beta }, \nonumber \\ \mathcal{O}^{ \mu e}_{eW }= & {} y_\mu (\overline{L}_\mu \vec {\tau }^a H \sigma ^{\alpha \beta } E_e ) W^a_{\alpha \beta } \end{aligned}$$

(100)

$$\begin{aligned} \mathcal{O}^{e \mu }_{eB }= & {} y_\mu (\overline{L}_e H \sigma ^{\alpha \beta } E_\mu ) B_{\alpha \beta },\nonumber \\ \mathcal{O}^{\mu e}_{eB }= & {} y_\mu (\overline{L}_\mu H \sigma ^{\alpha \beta } E_e ) B_{\alpha \beta } , \end{aligned}$$

(101)

$$\begin{aligned} \mathcal{O}^{(1) e\mu }_{HL }= & {} i(\overline{L}_e \gamma ^\alpha L_\mu ) (H^\dagger \mathop { D_\alpha }\limits ^{ \leftrightarrow } H),\qquad \qquad \end{aligned}$$

(102)

$$\begin{aligned} \mathcal{O}^{(3)e\mu }_{HL }= & {} i(\overline{L}_e \gamma ^\alpha \vec {\tau }L_\mu ) (H^\dagger \mathop { D_\alpha }\limits ^{ \leftrightarrow } \vec {\tau } H),\qquad \qquad \end{aligned}$$

(103)

$$\begin{aligned} \mathcal{O}^{e\mu }_{HE }= & {} i(\overline{E}_e \gamma ^\alpha E_\mu ) (H^\dagger \mathop { D_\alpha }\limits ^{ \leftrightarrow } H),\qquad \qquad \end{aligned}$$

(104)

where $i(H^\dagger \mathop { D_\alpha }\limits ^{ \leftrightarrow } H) \equiv i(H^\dagger D_\alpha H) - i( D_\alpha H)^\dagger H$, and $D_\alpha = \partial _\alpha + i \frac{g}{2}W_\alpha ^a \tau ^a + i \frac{g'}{2}YB_\alpha$. (The sign in the covariant derivative fixes the sign of the penguin operator and the SM Z vertex.) These signs cancel in matching at $m_{_{W}}$, so the results of Sect. 4 should be convention-independent.

This covariant derivative leads to $D_\alpha = \partial _\alpha + ieQA_\alpha$ after electroweak symmetry breaking, giving a Feynman rule for the photon-electron-electron vertex $ie\gamma ^\mu$. This choice (opposite to Peskin-Schroeder but agrees with Buras [47]), controls the sign of the QED anomalous dimensions mixing four-fermion operators to the dipole.