Radially excited states of $\eta _c$

Abstract

In the framework of chiral quark model, the mass spectrum of $\eta _c(ns)~(n=1,\ldots ,6)$ is studied with Gaussian expansion method. With the wave functions obtained in the study of the mass spectrum, the open flavor two-body strong decay widths are calculated by using the $^3P_0$ model. The results show that the masses of $\eta _c(1S)$ and $\eta _c(2S)$ are consistent with the experimental data. The explanation of $X(3940)$ as $\eta _c(3S)$ is possible because the decay width of $\eta _c(3S)$ is in the range of the experimental value of $X(3940)$. Although the mass of $X(4160)$ is about 110 MeV less than that of $\eta _c(4S)$ and the decay width of $X(4160)$ is much larger than that of $\eta _c(4S)$, the assignment of $X(4160)$ as $\eta _c(4S)$ cannot be excluded due to the large uncertainty of the experimental decay width and the compatibility of the branching ratios of $\eta _c(4S)$ with that of $X(4160)$, and the mass of $\eta _c(4S)$ can be shifted downwards by taking into account the coupling effect of the open charm channels. There are still no good candidates to $\eta _c(5S)$ and $\eta _c(6S)$.

1 Introduction

In recent years, a lot of charmonium-like states, the so-called “$XYZ$” states [1], have been observed by Belle, BaBar, BESIII, and other collaborations. Most of them cannot be accommodated in the quark models as conventional mesons because of their exotic properties. It has stimulated extensive interest in the research field of hadron physics to reveal the underlying properties of these states.

In the newest compilation of the Particle Data Group (PDG) [2], 35 states were listed under the $c\bar{c}$ section. Ten states were assigned, $\eta _c(1S)$, $\eta _c(2S)$, $J/\Psi (1S)$, $\Psi (2S)$, $\chi _{c0}(1P)$, $\chi _{c0}(2P)$, $\chi _{c1}(1P)$, $\chi _{c2}(1P)$, $\chi _{c2}(2P)$, and $h_c(1P)$, although there are some controversies about the assignment of $\chi _{c0}(2P)$ [3–7]. Experimentally there is no sign of $X(3915)\rightarrow D\bar{D}$, which strongly contradicts the theoretical expectation of $\chi _{c0}(2P)$, where the $D\bar{D}$ decay channel should dominate. In addition, the present analyses strongly favor the following assignments: $\psi (3770)$ as $1^3D_1$, $\psi (4040)$ as $3^3S_1$, $\psi (4160)$ as $2^3D_1$ and $\psi (4415)$ as $4^3S_1$ [8, 9]. The quantum numbers of $X(3872)$ were fixed recently, $I^G(J^{PC})=0^+(1^{++})$, so it is a good candidate of $\chi _{c1}(2P)$ [10] although there are also some arguments as regards this assignment [11–13]. The explanations of $X(3940)$ as $\eta _c(3S)$ [14], $X(4140)$ as $\chi _{c0}(3P)$ [7] were also proposed recently. However, about half of the $c\bar{c}$ states remain unassigned.

To assign the state reported by experimental collaborations to a theoretical one, firstly the experimental and theoretical masses of the state should be in agreement with each other, and secondly the measured and calculated decay properties of the state should be comparable. In the present work, the $\eta _c(nS)~(n=1,\ldots ,6)$ states are studied. The first two states of $\eta _c$ are well established. The other states need to be assigned. To validate the assignment of $\eta _c(nS)~(n=3,\ldots ,6)$, the more rigorous way is to calculate the decay widths of these states. In the present work we study the open charm two-body strong decay widths of all the $\eta _c(nS)~(n=3,\ldots ,6)$ mesons systematically in a constituent quark model. The spectrum of these $\eta _c(nS)~(n=1,\ldots ,6)$ mesons is obtained by using a high-precision few-body method, the Gaussian expansion method (GEM) [15], in the framework of chiral quark model [16]. In the GEM all the interactions are treated equally rather than some interactions: the spin–orbit and tensor terms are treated perturbatively in other approaches. The decay amplitudes to all open charm two-body modes that are nominally accessible are derived with the $^3P_0$ model. In the numerical evaluation of the transition matrix elements of decay widths, the wavefunctions obtained in the study of the meson spectrum, rather than the simple harmonic oscillator (SHO) ones, are used. It is expected that one may validate the assignment of the radially excited charmonia with spin–parity $J^{PC}=0^{-+}$ and may provide useful information for experiments to search the still missing states.

This work is organized as follows: In Sect. 2, the chiral quark model and wavefunctions of meson are presented; the $^3P_0$ decay model is briefly reviewed in Sect. 3; In Sect. 4, the numerical results of the two-body decays of $\eta _{c}(nS)(n=3,\ldots ,6)$ are obtained and presented with discussions; and the last section is a short summary.

2 The chiral quark model and wave functions

The chiral quark model, which has given a good description of hadron spectra [16, 17], is used to obtain the masses and wavefunctions of $\eta _c$. The Hamiltonian of the model for the meson is taken from Ref. [16],

$$\begin{aligned} \begin{aligned}&H_{q\bar{q}}(\mathbf {r}) = m_1+m_2+\frac{p_{\mathrm{r}}^2}{2\mu }+V_{12} \\&V_{12} = V^{C}_{12}+V^{OGE}_{12}+V^{\pi }_{12}+V^{K}_{12}+V^{\eta }_{12}+V^{\sigma }_{12}, \end{aligned} \end{aligned}$$

(1)

where $m_1$ and $m_2$ are the masses of quark and antiquark, $p_\mathrm{r}$ denotes the relative momentum between quark and antiquark, and $V_{12}$ is the interaction between quark and antiquark. In the present version of the chiral quark model, the screened color confinement potential is used,

$$\begin{aligned} V_{12}^{C}=\lambda _1 \cdot \lambda _2 [-a_c(1-\mathrm{e}^{-\mu _c r})+\Delta ], \end{aligned}$$

(2)

where $\mu _c=0.70 \,\mathrm{fm}^{-1}$ and $\Delta =181.10$ MeV. The channel coupling effect of $D\bar{D}$ etc. is taken into account partly according to Ref. [18]. The masses and the wavefunctions of mesons can be obtained by solving the Schrödinger equation,

$$\begin{aligned} H\Psi _{JM_J}=E \Psi _{JM_J}. \end{aligned}$$

(3)

The wavefunction $\Psi _{JM_J}$ can be written as the direct product of orbital, color, flavor, and spin wavefunctions,

$$\begin{aligned} \begin{aligned}&\Psi _{JM_J} = \left[ \psi _{L}(\mathbf {r})\chi _{S} \right] _{JM_J} \phi (q\bar{q})\omega (q\bar{q}), \\&\left[ \psi _{L}(\mathbf {r})\chi _{S}\right] _{JM_J} = \sum _{M_L,M_S} \langle LM_LSM_S|JM_J\rangle \psi _{LM_L}(\mathbf {r})\chi _{SM_S}, \end{aligned} \end{aligned}$$

(4)

where $\langle LM_LSM_S|JM_J\rangle$ is the Clebsch–Gordan coefficient, $\chi _{SM_S}$, $\phi (q\bar{q})$, and $\omega (q\bar{q})$ are spin, flavor, and color wavefunctions of meson, respectively. The Gaussian basis functions are employed to expand the orbital wavefunction $\psi _{LM_L}(\mathbf {r})$ [15],

$$\begin{aligned} \psi _{LM_L}(\mathbf {r})= & {} \sum _{k=1}^{k_{\max }}C_{Lk}\phi ^G_{LMk}(\mathbf {r}),\end{aligned}$$

(5)

$$\begin{aligned} \phi ^G_{LMk}(\mathbf {r})= & {} N_{Lk}r^L\exp (-\nu _{k}r^2)\mathbf {Y}_{LM_L}(\hat{\mathbf {r}}). \end{aligned}$$

(6)

The normalization constant $N_{Lk}$ is

$$\begin{aligned} N_{Lk}=\left[ \frac{2^{L+2}(2\nu _k)^{L+{\frac{3}{2}}}}{\sqrt{\pi }(2L+1)!!}\right] ^{\frac{1}{2}} \quad (k=1,\ldots ,k_{\max }). \end{aligned}$$

(7)

The Gaussian size parameters are in geometric progression,

$$\begin{aligned} \nu _k = \frac{1}{r_{k}^2},\quad r_k = r_1 a^{k-1} (k=1,\ldots ,k_{\max }), \end{aligned}$$

(8)

where $r_1=0.001$ fm, $r_{\max }=5.000$ fm, and $k_{\max }=30$ are used to arrive at the convergent results. Substituting Eqs. (4–6) into Eq. (3), we obtain a general eigen-equation,

$$\begin{aligned} \mathbf {H}\mathbf {c}=E\mathbf {N}\mathbf {c}, \end{aligned}$$

(9)

where $\mathbf {H}$ and $\mathbf {N}$ are the hamiltonian and overlap matrices, respectively.

3 Strong decay and quark-pair-creation model

To calculate the open flavor two-body strong decay widths of hadrons, the quark-pair-creation model, or $^3P_0$ model, is widely used. In this model, the hadron decay occurs via quark–antiquark pair production from the hadronic vacuum, so the quantum numbers of the created quark pair are of the hadronic vacuum, $J^{PC}=0^{++}$. This model has given a rather good description of the open flavor two-body strong decay width of hadrons [19–24], which are allowed by the Okubo–Zweig–Iizuka (OZI) rule. Here the model is used to calculate the open charm two-body strong decay widths of the radially excited states of $\eta _{c}(nS),(n=3,\ldots ,6)$. The transition operator used in the model [19] is

$$\begin{aligned} T= & {} -3~\gamma \sum _m\langle 1m1-m|00\rangle \int \,\mathrm{d}\mathbf {p}_3\,\mathrm{d}\mathbf {p}_4\delta ^3(\mathbf {p}_3+\mathbf {p}_4)\nonumber \\&\times \, \mathcal{{Y}}^m_1\left( \frac{\mathbf {p}_3-\mathbf {p}_4}{2}\right) \chi ^{34}_{1-m}\phi ^{34}_0\omega ^{34}_0b^\dagger _3(\mathbf {p}_3)d^\dagger _4(\mathbf {p}_4). \end{aligned}$$

(10)

The created pair is characterized by a color-singlet wave function $\omega ^{34}_0$, a flavor-singlet function $\phi ^{34}_{0}$, a spin-triplet function $\chi ^{34}_{1-m}$, and an orbital wave function $\mathcal{{Y}}^m_l(\mathbf {p})\equiv |p|^lY^m_l(\theta _p,\phi _p)$, which is the $l$th solid spherical harmonic polynomial. $\mathbf {p}_3$ and $\mathbf {p}_4$ denote the momenta carried by the quark and antiquark created from the vacuum. The strength of the quark-pair creation $\gamma$ from the vacuum is determined from the measured partial decay widths. In the present calculation, $\gamma$ is determined by fitting the open flavor two-body strong decay widths of the four established states $\psi (4040)$, $\psi (3770)$, $\psi (4160)$, and $\chi _{c2}(2P)$ and the decay widths are showed in Table 1. Here $\gamma _n=4.19$ for $u\bar{u},~d\bar{d}$ pairs and $\gamma _s=\gamma _n/\sqrt{3}$ for $s\bar{s}$ pairs, which values are different from Refs. [4, 7].

Table 1 The open flavor two-body strong decay widths of four states used to determine $\gamma$. The masses of mesons involved take the experimental values (unit in MeV)

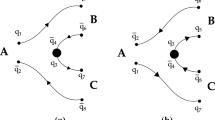
For the process $A\rightarrow B+C$, the $S$-matrix element is defined as

$$\begin{aligned} \langle BC|S|A\rangle =I-2\pi i\delta (E_A-E_B-E_C)\langle BC|T|A\rangle , \end{aligned}$$

(11)

where the T-matrix element is

$$\begin{aligned} \langle BC|T|A\rangle =\delta ^3(\mathbf {P}_A-\mathbf {P}_B-\mathbf {P}_C)\mathcal{{M}}^{M_{J_A}M_{J_B}M_{J_C}}, \end{aligned}$$

(12)

$\mathbf {P}_A$, $\mathbf {P}_B$, and $\mathbf {P}_C$ are the momenta of mesons A, B, and C, respectively, and $\mathcal{{M}}^{M_{J_A}M_{J_B}M_{J_C}}$ is the helicity amplitude for the process $A\rightarrow B + C$.

In experiments, the partial wave decay widths are often used, one can write

$$\begin{aligned} \Gamma = \sum _{JL} \Gamma _{JL}, \quad \Gamma _{JL}=\pi ^2 \frac{{|\mathbf P |}}{M_A^2}|\mathcal {M}^{JL}|^2. \end{aligned}$$

(13)

By the Jacob–Wick formula [25, 26], the partial wave amplitude $\mathcal{{M}}^{JL}$ can be further related to the helicity amplitude $\mathcal{{M}}^{M_{J_A}M_{J_B}M_{J_C}}$,

$$\begin{aligned}&{\mathcal {M}}^{J L}(A\rightarrow BC) = \frac{\sqrt{2 L+1}}{2 J_A +1} \sum _{M_{J_B},M_{J_C}} \langle L 0 J M_{J_A}|J_A M_{J_A}\rangle \nonumber \\&\quad \times \langle J_B M_{J_B} J_C M_{J_C} | J M_{J_A} \rangle \mathcal {M}^{M_{J_A} M_{J_B}M_{J_C}}({\mathbf {P}}), \end{aligned}$$

(14)

where $\mathbf {J}=\mathbf {J}_B+\mathbf {J}_C$, $\mathbf {J}_{A} =\mathbf {J}_{B}+\mathbf {J}_C+\mathbf {L}$, $M_{J_A}=M_{J_B}+M_{J_C}$, and $\mathbf {P}=\mathbf {P}_B=-\mathbf {P}_C$ is the three momentum of the daughter mesons $B$ and $C$ in the center-of-mass frame of meson A,

$$\begin{aligned} |\mathbf P |=\frac{\sqrt{[M^2_A-(M_B+M_C)^2][M^2_A-(M_B-M_C)^2]}}{2M_A}.\nonumber \\ \end{aligned}$$

(15)

4 Numerical calculation

The masses of the involved mesons and the corresponding wavefunctions are obtained by solving the general eigen-equation (9). The running strong-coupling constants are taken from Ref. [7] and the other parameters are taken from Ref. [16]. The masses of the open charm mesons and charmonium $\eta _{c}(nS),(n=1,\ldots ,6)$ are shown in Table 2. For charmonium and most open charm mesons, there is good agreement between experimental data and theoretical results. For several open charm mesons, the theoretical masses deviate from the experimental data by a few percent.

Table 2 The masses of the open charm mesons and charmonium $\eta _c$ (unit in MeV)

To justify the assignment, the decay width is very important. The open charm two-body strong decay modes and decay channels of $\eta _{c}(nS)(n=3,\ldots ,6)$ allowed by the phase space and OZI law are listed in Table 3. The open charm two-body decay widths of $\eta _{c}(nS)(n=3,\ldots ,6)$ are calculated and also shown in the fourth column of Table 3. In calculating the decay widths, the theoretical masses of the mesons involved and the corresponding wave functions obtained in solving the Schrödinger equations are used. In this way, the calculation of the widths is more self-consistent than most of the previous works, where the SHO wave functions are used. According to Ref. [7], the decay width is sensitive to the masses of the mesons, especially around the threshold of the decay. For comparison, the results of using experimental masses of mesons in the calculation of the decay widths are also shown in Table 3 (the fifth column).

Table 3 The open charm two-body strong decay modes and decay widths of the possible charmonium states of $\eta _{c}(nS)(n=3, \ldots , 6)$ allowed by the OZI rule and phase space (unit in MeV). The widths in the fourth column are derived with the theoretical masses of the initial state and the final ones. The widths in the fifth column are derived with the experimental masses. The widths in the sixth column are from Ref. [4]

From Tables 2 and 3, one can see that the mass and the open charm two-body decay width of $\eta _{c}(3S)$ are 4007 and 72 MeV, respectively. Under the constraint of the quantum numbers of $\eta _{c}(3S)$ and the mass of the state, the possible candidate is $X(3940)$. The calculated mass and the decay width of $\eta _{c}(3S)$ are all a little larger than the experimental data of $X(3940)$, $M=3942^{+7}_{-6}\pm 6$ MeV, $\Gamma =37^{+26}_{-15} \pm 8$ MeV. If the theoretical mass of $\eta _{c}(3S)$ and the experimental masses of the final states are used, the decay width will reduce to 65 MeV. If the mass of $\eta _{c}(3S)$ is shifted to 3940 MeV by coupling to the $D\bar{D}^*$ channels, the decay width will rise to ${\sim }98$ MeV. Taking the uncertainty of the model calculation and the experimental data, it is possible to assign $X(3940)$ as $\eta _{c}(3S)$. In Ref. [4], the mass of $\eta _{c}(3S)$ is 4043 MeV which is 40 MeV higher than our result. In this case the decay channel to $D^*\bar{D}^*$ opens and it contributes 33 MeV to the total decay width. Their total decay width is 80 MeV, which is consistent with our calculation. In Ref. [14], the mass of $\eta _{c}(3S)$ was estimated from the spectrum pattern and SHO wavefunction was used in evaluating the transition matrix element, so the decay width of $\eta _{c}(3S)$ is around the experimental value of $X(3940)$ with appropriate SHO parameter $R$. To confirm the assignment, more detailed studies are needed.

For $\eta _{c}(4S)$, the mass is 4276 MeV, and the decay width is around 27 MeV. Now the decay of $\eta _{c}(4S)$ to $D^{*}\bar{D}^{*}$ is allowed by the phase space and it is the main open flavor two-body strong decay channel. In Ref. [4], the mass of $\eta _{c}(4S)$ is 4384 MeV, which is about 110 MeV higher than the result of this work, so that there are more decay modes allowed by phase space. Its total decay width is about twice of our result. The possible candidate of $\eta _{c}(4S)$ is $X(4160)$, although its mass is about 110 MeV less than the theoretical mass of $\eta _c(4S)$. This is because the coupling effect of the open charm channels is expected to shift the mass of $\eta _c(4S)$ a little lower (a mass shift 205 MeV is obtained in the channel-coupling calculation with ground state $D\bar{D}^*$, $D_s\bar{D}_s^*$, $D^*\bar{D}^*$, etc.). The decay width of $X(4160)$ is 139$^{+111}_{-61}\pm 21$ MeV with $D^*\bar{D}^*$ mode seen and $D\bar{D}$, $D\bar{D}^*+c.c.$ mode not seen. So the open flavor two-body strong decay width of $\eta _c(4S)$ is much smaller than the experimental value of $X(4160)$. The more important information of the decay is the branching ratio. For the state $\eta _c(4S)$, the decay to $D\bar{D}$ is forbidden by the angular momentum coupling and the branching ratio $\frac{\Gamma (\eta _c(4S))\rightarrow D^*\bar{D}+c.c.)}{\Gamma (\eta _c(4S)\rightarrow D^*\bar{D}^*)}=0.014$. For the state $X(4160)$, for the experimental branching ratios we have $\frac{\Gamma (X(4160)\rightarrow D\bar{D})}{\Gamma (X(4160)\rightarrow D^*\bar{D}^*)}<0.09$ and $\frac{\Gamma (X(4160)\rightarrow D^*\bar{D}+c.c.)}{\Gamma (X(4160)\rightarrow D^*\bar{D}^*)}<0.22$, which are compatible with that of $\eta _c(4S)$. Taking into account the large uncertainty of the experimental decay width of $X(4160)$, the assignment of $X(4160)$ as $\eta _{c}(4S)$ cannot be excluded. This statement is different from the results of Ref. [14], where the SHO wavefunctions are used to calculate the transition matrix elements. For the excited state, the SHO approximation is not a reasonable one.

For $\eta _{c}(5S)$ and $\eta _{c}(6S)$ states, the decay to $0^- + 0^+$, $0^- + 2^+$ and $1^- + 1^+$ (even $1^- + 2^+$ for $\eta _{c}(6S)$) are allowed by the phase space. Moreover, they are the main decay modes of the $\eta _{c}(5S)$ and $\eta _{c}(6S)$ states. Comparing with the experimental data, we cannot find any states with these properties. Further measurements are expected to identify these two states.

Generally, for a specific decay channel with large decay momentum $P$ (Eq. (15)), the partial widths of the states $\eta _c(nS)$ decrease with the increase of $n$, e.g., $D_s\bar{D}_s^*$, $D^*\bar{D}^*$. This can be explained by the behavior of the transition amplitude, which is proportional to the factor $P\exp (-\zeta ^2 P^2)$ in $^3P_0$ model. However, our calculation shows that the statement cannot be applied to $D\bar{D}^*$ channel. For $\eta _c(3S) \rightarrow D\bar{D}^*$, the partial decay width is rather large, 72 MeV, whereas the width of $\eta _c(4S) \rightarrow D\bar{D}^*$ is very small and $\Gamma (\eta _c(4S) \rightarrow D\bar{D}^*) < \Gamma (\eta _c(5S) \rightarrow D\bar{D}^*) < \Gamma (\eta _c(3S) \rightarrow D\bar{D}^*)$. To justify the calculation, the details of the wavefunctions of $\eta _c(nS)(n=3,\ldots ,6)$ are needed. In Fig. 1, the wavefunctions of the states in momentum space are shown. The contribution of the wavefunction to the amplitude comes from the part with effective momentum (the momentum is larger than the decay momentum, which is shown as a vertical line in the figure). For the state $\eta _c(4S)$, a strong cancelation occurs because of the oscillation of the wavefunction in the part with effective momentum. For $\eta _c(5S)$, the cancelation can be ignored, and for $\eta _c(6S)$, no cancelation occurs.

Fig. 1

The wavefunctions of $\eta _c(nS)(n=3,\ldots ,6)$ in the momentum space. The vertical lines represent the decay momentum for the decay mode $D\bar{D}^*$ of the states

5 Summary

In this work, we study the mass spectra of $\eta _c(nS)~(n=1,\ldots ,6)$ with Gaussian expansion method in the framework of chiral quark model and calculate the open charm two-body strong decays of $\eta _c(nS)~(n=3,\ldots ,6)$ with $^3P_0$ model. The results show that the masses of $\eta _c(1S)$ and $\eta _c(2S)$ are consistent with the experimental data. The explanation of $X(3940)$ as $\eta _c(3S)$ is possible because the decay width of $\eta _c(3S)$ is in the range of experimental value of $X(3940)$. Although the mass of $X(4160)$ is about 110 MeV less than that of $\eta _c(4S)$ and the decay width of $X(4160)$ is much larger than that of $\eta _c(4S)$, the assignment of $X(4160)$ as $\eta _c(4S)$ cannot be excluded because the coupling effect of open charm channels may shift the mass of $\eta _c(4S)$ lower, and the experimental decay width has a large uncertainty, and the branching ratios of $\eta _c(4S)$ are compatible with that of $X(4160)$.

Because of the opening of open charm decay, the spectra of $\eta _c(nS)~(n=3,\ldots ,6)$ are still not as clear as the bottomonium. To describe the excited spectrum of charmonium, more consistent calculations are needed because the decay widths are sensitive to the details of wavefunctions. The conventional quark model needs to be extended. To develop the quark model, the effect of quark–antiquark-pair creation should be taken into account. For open flavor two-body decay model, $^3P_0$ model, the improvement is also needed. The dependence of strength $\gamma$ on the momentum of the created quark has been used to improve the agreement between theoretical results and experimental data [27]. A dynamic model for the meson decay is also expected to be fruitful. The study of the properties of $\eta _c(nS)~(n=1,\ldots ,6)$ is helpful for understanding the possible exotic, “$XYZ$” states.