Skip to main content
SpringerLink
Log in

First-principles study of the optical properties of PbTiO3

  • Solid and Condensed State Physics
  • Published:
The European Physical Journal B - Condensed Matter and Complex Systems Aims and scope Submit manuscript

Abstract.

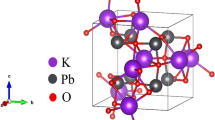
The optical properties of PbTiO3 were studied from first principles using the density functional theory. The dielectric functions and optical constants are calculated using the full potential–linearized augmented plane wave (FP-LAPW) method with the generalized gradient approximation (GGA). The theoretical calculated optical properties and energy loss (EEL) spectrum yield a static refractive index of 2.83 and a plasmon energy of 23.1 eV for cubic phase. The effective electron number at low energy saturates near 20 eV with the value of 18.1 for the effective electron number. In the tetragonal phase the static refractive index decreases to 2.59 and yields a plasmon energy of 22.7 eV.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  • P. Blaha, D. Singh, P.I. Sorantin, K. Schwarz, Phys. Rev. B 46, 1321 (1992)

    Article  Google Scholar 

  • J.F. Scott, C.A. Paz de Araujo, Science 246, 144 (1986)

    Google Scholar 

  • R.J. Nelmes, W.F. Kuhs, Solid State Commun. 54, 721 (1985)

    Article  Google Scholar 

  • J.P. Perdew, J.A. Chevary, S.H. Vosko, K.A. Jackson, M.R. Pederson, D.J. Singh, C. Fiolhais, Phys. Rev. B 46, 6671 (1992)

    Article  Google Scholar 

  • M. Peterson, F. Wanger, L. Hufnagel, M. Scheffler, P. Blaha, K. Schwarz, Comput. Phys. Commun. 126, 294 (2000)

    Article  Google Scholar 

  • P. Blaha, K. Schwarz, WIEN2k, Vienna University of Technology Austria (2002)

  • F. Wooten, Optical properties of solids (Academic Press, New York, 1972)

  • S.M. Hosseini, T. Movlarooy, A. Kompany submitted for press

  • U.V. Waghmare, K.M. Rabe, Phys. Rev. 55, 6161 (1997)

    Article  Google Scholar 

  • W. Kleemann, F.J. Schäfer, D. Rytz, Phys. Rev. B 34, 7873 (1986)

    Article  Google Scholar 

  • E.R. Leite, L.P.S. Santos, N.L.V. Carreo, E. Longo, C.A. Paskocimas, J.A. Varela, F. Lanciott, C.E.M. Campos, P.S. Pizam, Appl. Phys. Lett. 78, 2148 (2001)

    Article  Google Scholar 

  • S. Loughin, R.H. French, L.K. De Noyer, W.-Y Ching, Y.-N Xu J. Phys. D: Appl. Phys. 29, 1740 (1996)

    Google Scholar 

  • X.T. Chen, H. Yamane, K. Kaya, J. Phys. III France 2, 1439 (1992)

    Article  Google Scholar 

  • M.P. Moretm M.A.C. Devillers, K. Worhoff, P.K. Larsen J. Appl. Phys. 92, 468 (2002)

    Google Scholar 

  • S. Singh, J.P. Remeika, J.R. Potopowicz, Appl. Phys. Lett. 20, 135 (1972)

    Article  Google Scholar 

  • K. Bammou, D. Khatib, F. Bensamka, MJCM, 2 (1) art15 (1999)

Download references

Author information

Authors and Affiliations

  1. Department of Physics, (Electroceramic and Material Laboratory), Ferdowsi University of Mashhad, Mashhad, Iran

    S. M. Hosseini, T. Movlarooy & A. Kompany

Authors
  1. S. M. Hosseini
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Movlarooy
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Kompany
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. M. Hosseini.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hosseini, S., Movlarooy, T. & Kompany, A. First-principles study of the optical properties of PbTiO3. Eur. Phys. J. B 46, 463–469 (2005). https://doi.org/10.1140/epjb/e2005-00275-3

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjb/e2005-00275-3

Keywords

Search

Navigation