Skip to main content
SpringerLink
Log in

Energy-time correlation of slowing-down neutrons

  • Special Article - Tools for Experiment and Theory
  • Published:
The European Physical Journal A Aims and scope Submit manuscript

Abstract

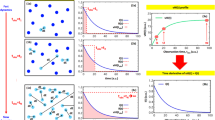
We formulate the energy-time correlation of neutrons slowing down through multiple elastic scatterings in a homogeneous infinite medium. From the correlation result, we obtain the neutron thermalisation time, expressed through special functions appearing in the calculation steps. We validate our theoretical approach by comparing the ensuing formulae with results of Monte Carlo calculations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K.S. Krane, Introductory Nuclear Physics (J. Wiley & Sons Inc., 1987) pp. 408--413

  2. A.A. Bergman, A neutron spectrometer based on measuring the slowing-down time of neutrons in lead, in Proceedings of the First International Conference on Peaceful Uses of Atomic Energy, Geneva, Vol. 4 (US Atomic Energy Commission, United Nations, New York, 1956) p. 135

  3. A. Abánades et al., Nucl. Instrum. Methods A 478, 577 (2002)

    Article  ADS  Google Scholar 

  4. Y. Danon et al., Nucl. Instrum. Methods B 261, 953 (2007)

    Article  ADS  Google Scholar 

  5. T. Granier et al., Nucl. Instrum. Methods A 506, 149 (2003)

    Article  ADS  Google Scholar 

  6. R. Pourimani et al., Nucl. Instrum. Methods A 488, 226 (2002)

    Article  ADS  Google Scholar 

  7. D. Rochman et al., Nucl. Instrum. Methods A 564, 400 (2006)

    Article  ADS  Google Scholar 

  8. D. Rochman et al., Nucl. Instrum. Methods A 550, 397 (2005)

    Article  ADS  Google Scholar 

  9. A.A. Bergman et al., Sov. Phys. JETP 6, 6 (1958)

    ADS  Google Scholar 

  10. N. Thiollière, Neutron elastic scattering cross-section measurement on carbon and fluorine in epithermal energy range using PEREN platform, PhD Thesis, Université Joseph Fourier, 2005 (in French)

  11. A.I. Hawari et al., Nucl. Instrum. Methods A 422, 846 (1999)

    Article  ADS  Google Scholar 

  12. R. Barjon, Physique des réacteurs nucléaires (Institut des Sciences Nucléaires, 1993) pp. 77--78

  13. R. Moreh et al., Phys. Rev. B 56, 187 (1997)

    Article  ADS  Google Scholar 

  14. P. Debye, Ann. Phys. (Leipzig) 39, 789 (1912)

    ADS  Google Scholar 

  15. I.G. Dyad’kin, E.P. Batalina, At. Energ. 10, 5 (1961)

    Google Scholar 

  16. M. Sawan, R.W. Conn, Nucl. Sci. Eng. 54, 127 (1974)

    Google Scholar 

  17. T.J. Williamson, R.W. Albrecht, Nucl. Sci. Eng. 42, 97 (1970)

    Google Scholar 

  18. D.G. Cacuci, Nucl. Sci. Eng. 108, 50 (1991)

    Google Scholar 

  19. Fermi age theory, described in K.H. Beckurts, K. Wirtz, Neutron Physics (Springer Verlag, 1964) p. 145 and in R. Barjon, Physique des réacteurs nucléaires (Institut des Sciences Nucléaires, 1993) p. 191

  20. E. Belle, Characterization of spallation neutron transport in a large lead volume - Differential flux and transmutation rate measurements, PhD Thesis, Université Joseph Fourier, 1998 (in French)

  21. G.E.P. Box, M.E. Muller, Ann. Math. Stat. 29, 610 (1958)

    Article  MATH  Google Scholar 

  22. P. Reuss Neutron Physics (EDP Sciences, 2008) p. 259

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut Polytechnique de Grenoble, LPSC, Université Joseph Fourier Grenoble 1, CNRS/IN2P3, 38000, Grenoble, France

    S. P. Chabod

Authors
  1. S. P. Chabod
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. P. Chabod.

Additional information

Communicated by N. Alamanos

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chabod, S.P. Energy-time correlation of slowing-down neutrons. Eur. Phys. J. A 44, 487–497 (2010). https://doi.org/10.1140/epja/i2010-10977-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epja/i2010-10977-y

Keywords

Search

Navigation