Skip to main content
SpringerLink
Log in

Choreographies in the discrete nonlinear Schrödinger equations

  • Regular Article
  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

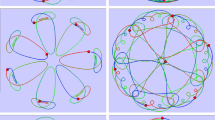
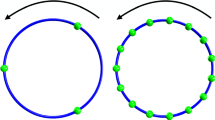
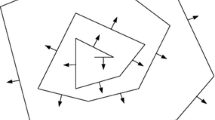
We study periodic solutions of the discrete nonlinear Schrödinger equation (DNLSE) that bifurcate from a symmetric polygonal relative equilibrium containing n sites. With specialized numerical continuation techniques and a varying physically relevant parameter we can locate interesting orbits, including infinitely many choreographies. Many of the orbits that correspond to choreographies are stable, as indicated by Floquet multipliers that are extracted as part of the numerical continuation scheme, and as verified a posteriori by simple numerical integration. We discuss the physical relevance and the implications of our results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A.V. Borisov, I.S. Mamaev, A.A. Kilin, Absolute and relative choreographies in the problem of point vortices moving on a plane, inRegular & Chaotic Dynamics (2004), Vol. 9, pp. 101–111

    Article  ADS  MathSciNet  Google Scholar 

  2. T. Bartsch, Q. Dai, B. Gebhard, SIAM J. Appl. Math. 78, 977 (2018)

    Article  MathSciNet  Google Scholar 

  3. T. Bartsch, Q. Dai, J. Differ. Equ. 260, 2275 (2016)

    Article  ADS  Google Scholar 

  4. V. Barutello, S. Terracini, Nonlinearity 17, 2015 2004

    Google Scholar 

  5. R. Calleja, E. Doedel, C. García-Azpeitia, to appear in Celest. Mech. Dyn. Astron.

  6. A. Chenciner, J. Fejoz, Regul. Chaotic Dyn. 14, 64 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  7. A. Chenciner, J. Gerver, R. Montgomery, C. Simó, Simple choreographic motions of N bodies: a preliminary study, in Geometry, Mechanics, and Dynamics, 60th birthday of J.E. Marsden, edited by P. Newton, P. Holmes, A. Weinstein (Springer-Verlag, 2002)

  8. A. Chenciner, R. Montgomery, Ann. Math. 152, 881 (2000)

    Article  MathSciNet  Google Scholar 

  9. D. Ferrario, S. Terracini, Invent. Math. 155, 305 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  10. C. García-Azpeitia, J. Ize, J. Differ. Equ. 252 5662 (2012)

    Article  ADS  Google Scholar 

  11. C. García-Azpeitia, J. Differ. Equ. Appl. 24, 564 (2016)

    Article  MathSciNet  Google Scholar 

  12. C. García-Azpeitia, J. Ize, DCDS-S 6, 975 (2013)

    Article  Google Scholar 

  13. C. García-Azpeitia, J. Ize, J. Differ. Equ. 254, 2033 (2013)

    Article  ADS  Google Scholar 

  14. T. Kapela, C. Simó, Nonlinearity 20, 1241 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  15. P. Kevrekidis,The discrete nonlinear Schrödinger equation. Mathematical Analysis, Numerical Computations and Physical Perspectives (Springer, 2009)

  16. F. Lederer, G.I. Stegeman, D.N. Christodoulides, G. Assanto, M. Segev, Y. Silberberg, Phys. Rep. 463, 1 (2008)

    Article  ADS  Google Scholar 

  17. F. Muñoz-Almaraz, E. Freire, J. Galán, E. Doedel, A. Vanderbauwhede, Physica D 181, 1 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  18. F. Le Clerc, L. Collot, M. Gross, Optics Lett. 25, 716 (2000)

    Article  ADS  Google Scholar 

  19. R. MacKay, S. Aubry, Nonlinearity 7, 1623 (1994)

    Article  ADS  MathSciNet  Google Scholar 

  20. C. Moore, Phys. Rev. Lett. 70, 3675 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  21. P. Panayotaros, D. Pelinovsky, Nonlinearity 21, 1265 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  22. C. Pando, E. Doedel, Physica D 238, 687 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  23. D. Pelinovsky, V. Rothos, Physica D 202, 16 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  24. C. Simó, New Families of Solutions in N-Body Problems, in European Congress of Mathematics (Springer Nature, 2001), pp. 101–115

  25. C.O. Weiss, R. Vilaseca, N.B. Abraham, R. Corbalán, E. Roldán, G.J. de Valcárcel, J. Pujol, U. Hübner, D.Y. Tang, Appl. Phys. B 61, 223 (1995)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas, Universidad Nacional Autónoma de México, México, Mexico

    Renato Calleja

  2. Department of Computer Science, Concordia University, Montreal, Canada

    Eusebius Doedel

  3. Facultad de Ciencias, Universidad Nacional Autónoma de México, México, Mexico

    Carlos García-Azpeitia

  4. Instituto de Física, Benemérita Universidad Autónoma de Puebla, Puebla, Mexico

    Carlos L. Pando L.

Authors
  1. Renato Calleja
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Eusebius Doedel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Carlos García-Azpeitia
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Carlos L. Pando L.
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Eusebius Doedel.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Calleja, R., Doedel, E., García-Azpeitia, C. et al. Choreographies in the discrete nonlinear Schrödinger equations. Eur. Phys. J. Spec. Top. 227, 615–624 (2018). https://doi.org/10.1140/epjst/e2018-00135-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjst/e2018-00135-x

Search

Navigation