Abstract
Bilayer ion-exchange membranes consisting of a thick heterogeneous membrane layer and a thin homogeneous membrane layer are studied theoretically and experimentally for their electrochemical properties such as overall and partial current–voltage curves, external and internal diffusion-limited currents, effective transference numbers, and specific selectivity for counterions and coions to be separated. For a diffusion layer (I)/modifying layer (II)/substrate membrane (III)/diffusion layer (IV) system in ternary solutions of electrolytes, we develop and verify a four-layer mathematical model with quasi-equilibrium boundary conditions. For the conditions of small current densities and limiting currents, we obtain analytical expressions for calculations of the limiting current, effective transference numbers, and specific selectivity coefficients. A numerical approach to calculating the specific selectivity coefficients is proposed. The mathematical model is verified for two electromembrane systems: one system is an anisotropic bilayer membrane with its MK-41 and MF-4SK polymer matrices having the same type of charge in a mixed CaCl2 + NaCl solution, and in another one its MA-41 and MF-4SK matrices have opposite types of charge in a mixed Na2SO4 + NaNO3 solution. The transport parameters of both the modifying film (MF-4SK) and initial membranes (MK-40 and MA-41) are determined in single-component and mixed electrolyte solutions in separate experiments.












Similar content being viewed by others
REFERENCES
J. Balster, R. Sumbharaju, S. Srikantharajah, et al., J. Membr. Sci. 287, 246 (2007).https://doi.org/10.1016/j.memsci.2006.10.042
K. Zhang, M. Wang, D. Wang, and C. Gao, J. Membr. Sci. 341, 246 (2009).
E. Molnár, N. Nemestóthy, and K. Bélafi-Bakó, Desalination 250, 1128 (2010).
H. Jaroszek and P. Dydo, Open Chem. 14, 1 (2016).
E. Güler, W. van Baak, M. Saakes, and K. Nijmeijer, J. Membr. Sci. 455, 254 (2014).
R. A. Tufa and S. Pawlowski, J. Veerman, et al., Appl. Energy 225, 290 (2018).
J. Grimm, D. Bessarabov, and R. Sanderson, Desalination 115, 285 (1998).
J. W. Post, J. Veerman, G. J. Hamelers, et al., J. Membr. Sci. 288, 218 (2007).
J. Veerman, R. M. Jong, M. Saakes, S. J. Metz, and G. J. Harmsen, J. Membr. Sci. 343, 7 (2009).
W. Tang, D. He, C. Zhang, P. Kovalsky, and T. D. Waite, Water Res. 120, 229 (2017).
X. F. Li, H. M. Zhang, Z. S. Mai, et al., Energy Environ. Sci. 4, 1147 (2011).
J. Sheng, A. Mukhopadhyay, W. Wang, and H. Zhu, Mater. Today Nano 7 (2019), 100044.
P. Y. Apel, O. V. Bobreshova, A. V. Volkov, V. V. Volkov, V. V. Nikonenko, I. A. Stenina, A. N. Filippov, Yu. P. Yampolskii, and A. B. Yaroslavtsev, Membr. Membr. Technol. 1, 45 (2019). https://doi.org/10.1134/S2517751619020021
Y. Qian, L. Huang, Y. Pan, X. Quan, et al., Sep. Purif. Technol. 192, 78 (2018).
S. V. Vinogradov, T. K. Bronich, and A. V. Kabanov, Adv. Drug Delivery Rev. 54, 135 (2002).
D. Schmaljohann, Adv. Drug Delivery Rev. 58, 1655 (2006).
Y. Qiu and K. Park, Adv. Drug Delivery Rev. 64, 49 (2012).
Y. Zhou, H. Yan, X. Wang, Y. Wang, and T. Xu, J. Membr. Sci. 520, 345 (2016). https://doi.org/10.1016/j.memsci.2016.08.011
Y. Chen, J. R. Davis, C. H. Nguyen, J. C. Baygents, and J. Farrell, Environ. Sci. Technol. 50, 5900 (2016). https://doi.org/10.1021/acs.est.5b05606
O. Nir, R. G. Sengpiel, and M. Wessling, Chem. Eng. J. 346, 640 (2018). https://doi.org/10.1016/j.cej.2018.03.181
C. Díaz Nieto, N. Palacios, K. Verbeeck, et al., Water Res. 154 (2019), 117. https://doi.org/10.1016/j.watres.2019.01.050
J. Ran, L. Wu, Y. He, Z. Yang, et al., J. Membr. Sci. 522, 267 (2017).https://doi.org/10.1016/j.memsci.2016.09.033
S. Lacour, V. Deluchat, J. C. Bollinger, and B. Serpaud, Talanta 46, 999 (1998).
T. Sata and W. Yang, J. Membr. Sci. 211, 177 (2003).
T. Sata, Ion Exchange Membranes: Preparation, Characterization, Modification and Application (Royal Society of Chemistry, 2007).
D. Ariono, J. Appl. Polym. Sci. 134, 45540 (2017).
D. V. Golubenko and A. B. Yaroslavtsev, J. Membr. Sci. 612, 118408 (2020). https://doi.org/10.1016/j.memsci.2020.118408
V. Zabolotskii, N. Sheldeshov, and S. Melnikov, J. Appl. Electrochem. 43, 1117 (2013).
A. Filippov, D. Petrova, I. Falina, N. Kononenko, et al., Polymers 10, 366 (2018). https://doi.org/10.3390/polym10040366
S. Abdu and M. Wessling, Appl. Mater. Interfaces 3, 1843 (2014). https://doi.org/10.1021/am4048317
R. Femmer, A. Mani, and M. Wessling, Sci. Rep. 5, 11583 (2015). https://doi.org/10.1038/srep11583
M. Wang and C.-J. Gao, Recent Pat. Chem. Eng. 4 (2011).
L. Ge, B. Wu, D. Yu, et al., Chin. J. Chem. Eng. 35, 1025 (2017).
S. Shkirskaya, M. Kolechko, and N. Kononenko, Curr. Appl. Phys. 15, 1587 (2015). https://doi.org/10.1016/j.cap.2015.09.017
T. Sata and R. Izuo, J. Membr. Sci. 45, 209 (1989).
D. V. Golubenko, Yu. A. Karavanova, S. S. Melnikov, et al., J. Membr. Sci. 563, 777 (2018). https://doi.org/10.1016/j.memsci.2018.06.024
I. Stenina, D. Golubenko, V. Nikonenko, and A. Yaroslavtsev, Int. J. Mol. Sci. 21, 5517 (2020). https://doi.org/10.3390/ijms21155517
S. T. Hwang and K. Kammermeyer, Techniques of Chemistry, vol. 7 : Membranes in Separation (Wiley, New York, 1975).
V. I. Zabolotsky and V. V. Nikonenko, Transport of Ions in Membranes (Nauka, Moscow, 1996) [in Russian].
F. Helfferich, Ion Exchange (McGraw-Hill, New York, 1962).
B. P. Nikol’skii and V. I. Paramonova, Usp. Khim. 8, 1535 (1939).
H. P. Gregor and D. M. Westone, J. Am. Chem. Soc. 86, 5689 (1964).
R. Schlögl, Z. Phys. Chem. 1, 305 (1954).
R. Schlögl, Ber. Busenges. Phys. Chem. 82, 225 (1978).
F. Conti and G. Eisenman, Biophys. J. 5, 511 (1965).
K. Kontturri and H. Pajari, Sep. Sci. Technol. 21, 1089 (1986).
A. M. Peers, Discuss. Faraday Soc. 21, 124 (1956).
A. M. Peers, J. Appl. Chem. 8, 59 (1958).
A. Di Benedetto and E. Lightfoot, Ind. and Eng. Chem. 50, 691 (1958).
Y. Oren and A. Ligtan, J. Phys. Chem. 78, 1805 (1974).
A. T. Di Benedetto and E. N. Lightfoot, A. I. Ch. E. J. 8, 79 (1962).
V. V. Nikonenko, V. I. Zabolotskii, and K. A. Lebedev, Elektrokhimiya 15, 1494 (1979).
V. V. Nikonenko, V. I. Zabolotskii, and K. A. Lebedev, Elektrokhimiya 16, 555 (1980).
K. A. Lebedev, V. V. Nikonenko, V. I. Zabolotskii, and N. P. Gnusin, Elektrokhimiya 22, 638 (1986).
L. Hou, J. Pan, D. Yu, B. Wu, et al., J. Mem. Sci. 528, 243 (2017).
V. I. Zabolotsky, J. A. Manzanares, V. V. Nikonenko, and K. A. Lebedev, Desalination 147, 387 (2002).
V. V. Nikonenko, V. I. Zabolotskii, and K. A. Lebedev, Elektrokhimiya 32, 258 (1996).
V. I. Zabolotskii, K. A. Lebedev, and I. V. Orel, Russ. J. Electrochem. 39, 1130 (2003). https://doi.org/10.1023/A:1026187823767
M. Vaselbehagh, H. Karkhanechi, R. Takagi, and H. Matsuy, J. Membr. Sci. 490, 301 (2015).https://doi.org/10.1016/j.memsci.2015.04.014
T. Luo, F. Roghmans, and M. Wesslin, J. Membr. Sci. 597, 117645 (2020). https://doi.org/10.1016/j.memsci.2019.117645
T. Sata, J. Membr. Sci. 167, 1 (2000). https://doi.org/10.1016/S0376-7388(99)00277-X
F. G. Donnan, Chem. Rev. 1, 73 (1924).
V. F. Gaiduk, Zhurn. Vychisl. Matem. Matem. Fiziki 24, 504 (1984).
I. S. Bakhvalov, N. P. Zhidkov, and G. I. Kobel’kov, Computational Methods (Nauka, Moscow, 1987) [in Russian].
K. Lebedev, P. Ramirez, S. Mafe, and J. Pellicer, Lengmuir 16, 9941 (2000).
V. I. Zabolotsky, A. R. Achoh, K. A. Lebedev, and S. S. Melnikov, J. Membr. Sci. 608, 118152 (2020). https://doi.org/10.1016/j.memsci.2020.118152
Nafion tm membranes and dispersions, www.chemours.com/ Nafion/en_US/index.html
V. I. Zabolotskii, S. S. Mel’nikov, and N. V. Shel’deshov, RF Patent, No. 2516160.
V. I. Zabolotskii, N. V. Shel’deshov, and M. V. Sharafan, Russ. J. Electrochem. 42, 1345 (2006).
V. G. Levich, Physicochemical Hydrodynamics (Fizmatgizb, Moscow, 1959) [in Russian].
E. R. Nightingale, J. Phys. Chem. 109, 1381 (1959). https://doi.org/10.1021/j150579a011
V. I. Zabolotskii, N. P. Gnusin, and G. M. Sheretova, Zh. Fiz. Khim. 59, 2467 (1985).
N. P. Berezina, N. A. Kononenko, O. A. Dyomina, and N. P. Gnusin, J. Colloid Interface Sci. 139, 3 (2008).
O. A. Demina, S. A. Shkirskaya, N. A. Kononenko, and E. V. Nazyrova, Russ. J. Electrochem. 52, 291 (2016). https://doi.org/10.1134/S1023193516040030
V. N. Afanas’ev and E. Yu. Tyunina, Russ. J. Gen. Chem. 74, 673 (2004).
A. A. Zavitsas, J. Phys. Chem. 109, 20636 (2005). https://doi.org/10.1021/jp053909i
A. N. Filippov, N. A. Kononenko, I. V. Falina, E. V. Titskaya, et al., Colloid J. 82, 81 (2020). https://doi.org/10.1134/S1061933X20010056
S. A. Mareev, E. Evdochenko, M. Wessling, et al., J. Mem. Sci. 603, 118010 (2020). https://doi.org/10.1016/j.memsci.2020.118010
Funding
This study was supported by the Russian Science Foundation, research project no. 19-13-00339.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by A. Kukharuk
APPENDICES
APPENDICES
Appendix 1 . Mathematical Algorithm for Solving the Boundary Value Problem
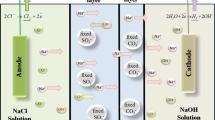
Consider two systems. The first system (α = 1) includes Ca2+ (1), Na+ (2) and Cl– (3) ions \(\left( {j = 1,2,3} \right)\); and the second one (α = 2) includes \({\text{SO}}_{{\text{4}}}^{{{\text{2}}-}}\) (1), \({\text{NO}}_{{\text{3}}}^{-}\) (2), and Na+ (3) ions. The membrane (III) and modifying layer (II) of the first system have the same charge of their ion-exchanging matrices (MK-40/MF-4SK). In the second system, the polymer matrix of the initial membrane and that of the modifying layer have opposite charges (MA-41/MF-4SK).
We can formulate a boundary value problem that embraces both the first and the second system, considering that the competing ions in the two systems function as counterions with respect to the initial membrane matrix and the modifying layer of the first system, whereas in the second system, they function as coions.
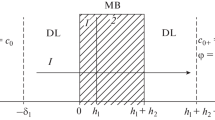
Transport equations are formulated as Nernst–Planck equations in the steady state form. It is assumed that the electroneutrality condition holds and that thermodynamic equilibrium is maintained locally, i.e., at the interfaces. The effects that manifest at high current densities, dissociation of water molecules, appearance of space charge layer near the interfaces, and the exaltation effect, were not considered. Let the electrical current with density i flow normally to the surface of the modified membrane that is interposed between two identical electrolyte solutions I and IV with ion concentrations \(c_{j}^{{\text{I}}} = c_{j}^{{{\text{IV}}}} = c_{j}^{0}{\text{.}}\) Competing ionic species 1 and 2 are counterions with respect to the ion-exchange matrix of the membrane, and ionic species with j = 3 is the coion. Let us choose a space coordinate system so that its origin coincides with the left boundary of diffusion layer I (x = 0). The width of the entire system is indicated by \(l = \delta + \tilde {d} + \bar {d} + \delta .\)
A boundary value problem for three ions (\(j = 1,2,3\)) with concentrations \({{c}_{1}}\left( x \right),\) \({{c}_{2}}\left( x \right)\) and \({{c}_{3}}\left( x \right)\) in four layers (\(m = {\text{I}},{\text{II}},{\text{III}},{\text{IV}}\)) is formulated in a scaled form. The Nernst–Planck equation holds in all four layers:
along with electroneutrality condition
For the diffusion layers, \({{Q}_{{\text{I}}}} = {{Q}_{{{\text{IV}}}}} = 0,\) and for the modifying film and the membrane, \(\tilde {Q} = {{Q}_{{{\text{II}}}}}\) and \(\bar {Q} = {{Q}_{{{\text{III}}}}}.\) For the whole system, the condition for the flow of electrical current is
Local thermodynamic equilibrium is assumed to be maintained at the interfaces. The imposition of condition of local thermodynamic equilibrium (continuity of the electrochemical potential) for all the interfaces in the electromembrane system leads to six boundary conditions. For the first diffusion layer I/modifying layer II boundary, we write
For the modifying layer II/membrane III boundary,
For the membrane III/second diffusion layer IV,
where \({{\left( {{{c}_{{j,s}}}} \right)}_{m}}\) is the ion concentration at the interfaces; and \(k_{{1,j}}^{{{\text{I}}{\text{,II}}}},\) \(k_{{1,j}}^{{{\text{II}}{\text{,III}}}}\) and \(k_{{1,j}}^{{{\text{III}}{\text{,IV}}}}\) are local thermodynamic equilibrium constants at the diffusion layer I/modifying layer II, modifying layer II/substrate membrane III, and substrate membrane III/diffusion layer IV interfaces, respectively.
The thermodynamic equilibrium constant at the modifying layer II/membrane III interface is expressed through two other equilibrium constants:
For counterions j = 1 and j = 2, boundary conditions (4)–(6) are described with an ion-exchange constant [41]; and for counterion j = 1 and coion j = 3, they are described by the Donnan equation [62].
The concentrations of all ionic species are defined at the outer boundaries of diffusion layers I (x = 0) and IV (x = l), which is a consequence of constancy of the ion concentrations in the solution bulk:
In Eqs. (1)–(8), \(c_{j}^{0}\) is the molar concentration of the j-th ionic species in the bulk of the solution on the left and right boundaries of the considered system; \({{j}_{j}}\) is flux density of the j-th ionic species; \({{\left[ {{{c}_{{j,s}}}} \right]}_{m}}\) are the boundary concentrations of the j-th ionic species in the m-th layer; \({{z}_{j}}\) is the charge number of the j-th ionic species; \({{\left[ {{{D}_{j}}} \right]}_{m}}\) are the diffusion coefficients of the j-th ionic species in the m-th layer; φ is the electric potential; \(l = 2\delta + \tilde {d} + \bar {d}\) is the length of a multilayer system; \(\delta \) is the thickness of diffusion layers; \({{\;}}\tilde {d}\) is the thickness of the modifying layer; \(\bar {d}\) is the thickness of the substrate membrane; and \(F,\) \(R\) and \(T\) have their conventional meaning.
Simultaneous Eqs. (1) with additional conditions (2) and (3) and boundary value conditions (4)–(8) make up a boundary value problem describing a four-layer membrane system.
This boundary value problem has a physical meaning if the current does not exceed its limiting value \(\left( {i \leqslant {{i}_{{{\text{lim}}}}}} \right).\) For thickness of modifying layer \(\tilde {d} = 0,\) this problem transforms into a boundary value problem describing a three-layer system with an isotropic membrane [54, 57].
To solve the problem for the four-layer membrane system, we used parallel shooting method [63–65] that we modified to use for solving multilayer boundary value problem (1)–(8). The procedure for solving this boundary value problem was described in [66].
Appendix 2
A concentration dependence of diffusion flux j obtained experimentally was used to calculate integral coefficient P of diffusional permeability of the membrane. The concentration dependences of integral diffusional permeability coefficients \({{P}_{j}}\) of the considered membrane in sodium sulfate and sodium nitrate solutions are shown in the figure in log–log coordinates.

Figure. Log–log plot of concentration dependences of the integral coefficient of diffusional permeability for MF-4SK in (1) Na2SO4 and (2) NaNO3 solutions.
To determine the diffusion coefficient of \({\text{SO}}_{{\text{4}}}^{{{\text{2}} - }}\) ions in a MF-4SK membrane placed in a Na2SO4 solution (γ = 1) and the diffusion coefficients of \({\text{NO}}_{{\text{3}}}^{ - }\) ions in a NaNO3 solution (γ = 2), let us write the following equation for diffusion flux of electrolyte from a solution with concentration \({{c}^{0}}\) into water (\(c\) = 0) across a membrane with thickness \(d\):
where \({{P}_{{{\gamma }}}}\) is the integral diffusional permeability of membrane, J = \(\left| {{{z}_{i}}{{j}_{i}}{{\;}}} \right|\) is the electrolyte flux, c = \(\left| {{{z}_{i}}j{{c}_{i}}{{\;}}} \right|\) is the equivalent solution concentration, \(\Delta c = {{c}^{{{\text{II}}}}} - {{c}^{{\text{I}}}},\) is the drop in concentration across the film, \(d\) is the film thickness, and \({{c}^{{\text{I}}}} = 0.\)
Differential diffusional permeability \(P_{{{\gamma }}}^{{\text{*}}}\) is defined by formula
The integral and differential permeability coefficients are related by equation
To simplify calculations, we seek a solution in the exponential form:
From Eqs. (3) and (4), we get:
Using membrane permeability \(P_{k}^{{\text{*}}}\) in type γ = 1, 2 electrolytes, we can estimate diffusion coefficients \({{\tilde {D}}_{j}},\) and \(\overline {{{D}_{j}}} \) of coion species j = 1, 2. For this, we use the notion of a virtual solution. According to it, \(P_{k}^{{\text{*}}}\) can be expressed through Onsager’s kinetic coefficients by formula
where γ = j = 1 for SO4 coions, γ = j = 2 for NO3 coions, and j = 3 for Na+ counterions in the two electrolytes. Taking into account that \(L_{3}^{{\text{*}}} \gg L_{j}^{{\text{*}}}\), we arrive at the approximate formula:
where \(L_{j}^{{\text{*}}} = \frac{{D_{j}^{{\text{*}}}c_{j}^{{\text{*}}}}}{{RT}}\) = \(\frac{{D_{j}^{{\text{*}}}c}}{{\left| {{{z}_{i}}} \right|RT}},\) \(j = 1,2.\)
Then, the diffusion coefficients for the modifying layer are calculated by the formula:
The values for diffusion coefficients of the MF-4SK membrane were determined for concentration c0 = 0.03 mol/L.
Rights and permissions
About this article
Cite this article
Achoh, A.R., Zabolotsky, V.I., Lebedev, K.A. et al. Electrochemical Properties and Selectivity of Bilayer Ion-Exchange Membranes in Ternary Solutions of Strong Electrolytes. Membr. Membr. Technol. 3, 52–71 (2021). https://doi.org/10.1134/S2517751621010029
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S2517751621010029