Abstract
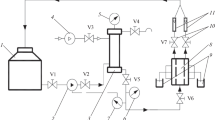
A mathematical model is proposed for separating liquids which contain acrylic dispersions and returning expensive technological components dissolved within them to the production cycle. The main limiting factor is the formation of a sediment layer on the membrane surface. This process is unsteady, because the thickness of the sediment layer varies both in the time of the separation process and in the length of the membrane module. The influence of the sediment layer on the hydrodynamics and mass transfer efficiency, its productivity, and the quality of purification is determined. The calculation of the sediment layer and its influence on the separation process is performed using the microprocess method. This method is based on material and energy balances and takes into account viscosity and diffusion coefficients, which vary depending on the temperature and composition of the mixture. The dependences of the sediment thickness on time and the length of the membrane module and selectivity coefficients on the concentration of the colloidal solution are obtained to determine the effective parameters of the baromembrane installation.










Similar content being viewed by others
REFERENCES
B. N. Mel’nikov, Theoretical Basis of Technology of Dyeing Fibrous Materials (Legkaya industriya, Moscow, 1978) [in Russian].
A. I. Rodionov, Yu. P. Kuznetsov, and G. S. Solov’ev, Protection of Biosphere from Industrial Emissions. Basics of Design of Technological Processes (Khimiya, KolosS, Moscow, 2005) [in Russian].
V. S. Beskov and V. S. Safronov, General Chemical Technology and Fundamentals of Industrial Ecology (Khimiya, Moscow, 1999) [in Russian].
G. V. Lepesh and A. S. Panasyuk, Tekhnik. Ekonom. Probl. Serv. 3, 14 (2016).
A. E. Tret’yakova, E. A. Chernogortsev, and V. V. Safonov, Tekhnol. Tekstil. Prom. 2, 127 (2016).
A. V. Nevskii, V. P. Meshalkin, and V. A. Sharnin, Analysis and Synthesis of Water Resource-Saving Chemical-Technological Systems (Nauka, Moscow, 2004) [in Russian].
Yu. I. Dytnerskii, Reverse Osmosis and Ultrafiltration (Khimia, Moscow, 1978) [in Russian].
S. V. Fedosov, V. A. Maslennikov, Yu. P. Osadchii, and A. V. Markelov, Vestn. Grazhd. Inzh. 5, 154 (2013).
V. I. Novikova, V. V. Kryachkova, and Yu. I. Tarasova, Membr. Membr. Tekhnol. 1, 127 (2019).
Yu. I. Dytnerskii, Baromembrane Processes (Khimiya, Moscow, 1986) [in Russian].
V. P. Dubyaga, L. P. Perepechkin, and E. E. Katalevskii, Polymer Membranes (Khimiya, Moscow, 1981) [in Russian].
S.-T. Hvang and K. Kammermejer, Membrane in Separation (Syndey, Toronto: A Wiley-Interscience Publication, John Wiley & Sons, New York, London, 1981).
A. Brou, L. Ding, P. Boulnois, and M. Y. Jaffrin, J. Membr. Sci. 197, 269 (2002).
C.-C. Ho and A. L. Zydney, J. Membr. Sci. 155, 261 (1999).
J. D. Nikolova and M. A. Islam, J. Membr. Sci. 146, 105 (1998).
W. Piatkiewicz, S. Rosinski, D. Lewinska, J. Bukowski, and W. Judycki, J. Membr. Sci. 153, 91 (1999).
J. H. Sung, M.-S. Chun, and H. J. Choi, J. Colloid Interface Sci. 264, 195 (2003).
M. Zhang and L. Song, J. Environ. Eng. 126, 667 (2000).
G. Belford and B. Marks, Desalination 28, 13 (1979).
W. F. Blatt, A. Dravid, A. S. Michaels, and L. Nelson, Membr. Sci. Technol. 9, 47 (1970).
M. Mulder, Basic Principles of Membrane Technology (Center for Membrane Science and Technology, University of Twente, Kluwer Academic, Netherlands, 1995).
J. G. Wijmans, S.-I. Nakao, J. W. A. van der Berg, F. R. Troelstra, and C. A. Smolders, J. Membr. Sci. 22, 117 (1985).
R. Figueroa, A. Cassano, and E. Drioli, Sep. Purify. Technol. 80, 1 (2011).
C. Tien and B. V. Ramarao, J. Chin. Inst. Chem. 37, 81 (2006).
C. Wang, Q. Li, H. Tang, D. Yan, W. Zhou, J. Xing, and Y. Wan, BioRes. Technol. 116, 366 (2012).
A. Salahi, M. Abbasi, and T. Mohammadi, Desalination 251, 153 (2010).
M. J. Corbatón-Báguena, S. Álvarez-Blanco, and M. C. Vincent-Vela. Desalination, 360, 87 (2015).
G. Segré and A. Silberberg, J. Fluid Mech. Digit. Arc. 115 (1962).
G. Segré and A. Silberberg, J. Fluid Mechanics Digital Archive, 136 (1962).
D. Houi and R. Lenormand, Filtr. Sep. 238 (1986).
M. Tassopoulos and J. A. O’Brien, II AIChE J. 35, 967 (1989).
Yu. P. Osadchii and V. N. Blinichev, Tekhnol. Tekstil. Prom. 7, 87 (1992).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by V. Avdeeva
Rights and permissions
About this article
Cite this article
Fedosov, S.V., Osadchy, Y.P. & Markelov, A.V. Modeling of Ultrafiltration Process Taking Into Account the Formation of Sediment on Membrane Surface. Membr. Membr. Technol. 2, 169–180 (2020). https://doi.org/10.1134/S251775162003004X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S251775162003004X