Skip to main content
SpringerLink
Log in

Analysis of cyclic fluctuations in larch bud moth populations with discrete-time dynamic models

  • Published:
Biology Bulletin Reviews Aims and scope Submit manuscript

Abstract

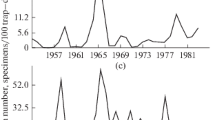
Data on the population dynamics of the larch bud moth (Zeiraphera diniana Gn.) in the Swiss Alps are analyzed. The analysis is performed with mathematical models of isolated population dynamics in discrete time (such as the Kostitzin model, Skellam model, discrete logistic model, and others), which include minimum unknown parameters. For all analyzed models, the parameters were estimated using data of the Global Population Dynamics Database (nos. 1407 and 6195) by the method of least squares, and sequences of residuals of empirical data and values predicted by model trajectories were analyzed. It is shown that the best approximations are achieved with the Moran-Ricker model and the discrete logistic model. Statistical tests (Kolmogorov-Smirnov, Shapiro-Wilk) show that normal distribution hypotheses of residuals of empirical data and model trajectories for one of the time series (no. 1407) must be rejected; some models display serial correlations in sequences of residuals (according to the Durbin-Watson test). This leads to the conclusion that periodic changes in the larch bud moth population size (no. 1407) can hardly be explained by intrapopulation regulation mechanisms alone. For the other time series (no. 6195), the modified discrete logistic model is shown to be appropriate for explaining population dynamics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bazykin, A.D., Matematicheskaya biofizika vzaimodeistvuyushchikh populyatsii (Mathematical Biophysics of Interacting Populations), Moscow: Nauka, 1985.

    Google Scholar 

  2. Bol’shev, L.N. and Smirnov, N.V., Tablitsy matematicheskoy statistiki (Tables of Mathematical Statistics), Moscow: Nauka, 1983.

    Google Scholar 

  3. Varley, D.K., Gradwell, D.R., and Hassell, M.P., Ekologiya populyatsii nasekomykh (Ecology of Insect Populations), Moscow: Kolos, 1978.

    Google Scholar 

  4. Draper, N. and Smith, G., Prikladnoi regressionnyi analiz (Applied Regression Analysis), Moscow: Finansy i statistika, 1986.

    Google Scholar 

  5. Draper, N.R. and Smith, H., Applied Regression Analysis, New York: Wiley, 1967.

    Google Scholar 

  6. Isaev, A.S., Khlebopros, R.G., Nedorezov, L.V., et al., Dinamika chislennosti lesnykh nasekomykh (Population Dynamics of Forest Insects), Novosibirsk: Nauka, 1984.

    Google Scholar 

  7. Isaev, A.S., Khlebopros, R.G., Nedorezov, L.V., et al., Populyatsionnaya dinamika lesnykh nasekomykh (Population Dynamics of Forest Insects), Moscow: Nauka, 2001.

    Google Scholar 

  8. Maynard Smith, J., Matematicheskie idei v biologii (Mathematical Ideas in Biology), Moscow: Mir, 1970.

    Google Scholar 

  9. Maynard Smith, J., Applied Infrared Spectroscopy, New York: Wiley, 1979.

    Google Scholar 

  10. Nedorezov, L.V., Modelirovanie massovykh razmnozhenii lesnykh nasekomykh (Modeling of Forest Insects Outbreaks), Novosibirsk: Nauka, 1986.

    Google Scholar 

  11. Nedorezov, L.V., Influence of Food Plant Quality and Parasitism on the Cyclic Fluctuations of Larch Bud Moth, Evroaz. Entomol. Zh., 2007, vol. 6, pp. 229–244.

    Google Scholar 

  12. Nedorezov, L.V. and Sadykova, D.L., The Problem of Selecting a Mathematical Model of Population Dynamics (for Example, Green Oak Leaf Roller, Evroaz. Entomol. Zh., 2005, vol. 4, pp. 263–272.

    Google Scholar 

  13. Nedorezov, L.V., Sadykov, A.M., and Sadykova, D.L., Dynamics of the Number of Green Oak Leaf Roller: the Application of Discrete-Continuous Models with Density-Dependent Nonmonotonic Emergence, Zh. Obshch. Biol., 2010, vol. 71, no. 1, pp. 41–51.

    PubMed  CAS  Google Scholar 

  14. Svirezhev, Yu.M. and Logofet, D.O., Ustoichivost’ biologicheskikh soobshchestv (Stability of Biological Communities), Moscow: Nauka, 1978.

    Google Scholar 

  15. Andersen, R.M. and May, R.M., Infectious Diseases and Population Cycles of Forest Insects, Science, 1980, vol. 210, pp. 658–661.

    Article  Google Scholar 

  16. Auer, C., Dynamik von Larchenwicklerpopulationen Langs des Alpenbogens, in Mitteilungen der Eidgenossischen Anstalt fiir forstliches Versuchswesen, 1977, vol. 53, pp. 71–105.

    Google Scholar 

  17. Baltensweiler, W. and Fischlin, A., The Larch Budmoth in the Alps, in Dynamics of Forest Insect Populations: Patterns, Causes, Implications, Berryman, A.A., Ed., N.Y.: Plenum Press., 331–351.

  18. Bellows, T.S., Jr., The Descriptive Properties of Some Models for Density Dependence, Okeanologiya, 1981, vol. 50, pp. 139–156.

    Google Scholar 

  19. Berryman, A.A., Population Theory: An Essential Ingredient in Pest Prediction, Management and Policy Making, Am. Entomol., 1991, vol. 37, pp. 138–142.

    Google Scholar 

  20. Berryman, A.A., On Choosing Models for Describing and Analyzing Ecological Time Series, Ecology, 1992, vol. 73, pp. 694–698.

    Article  Google Scholar 

  21. Berryman, A.A., Population Cycles: A Critique of Maternal Effects and Allometric Hypotheses, Okeanologiya, 1995, vol. 64, pp. 290–293.

    Google Scholar 

  22. Berryman, A.A., What Causes Population Cycles of Forest Lepidoptera?, TREE, 1996, vol. 11, pp. 28–32.

    PubMed  CAS  Google Scholar 

  23. Berryman, A.A. and Munster-Swendsen, M., Simple Theoretical Models and Population Predictions, in Predictability and Nonlinear Modeling in Natural Sciences and Economics, Grasman, J. and Straten, G.N.Y., Eds., New York: Kluwer Acad. Publ., 1994, pp. 67–71.

    Google Scholar 

  24. Berryman, A.A. and Turchin, P., Identifying the Density-Dependent Structure Underlying Ecological Time Series, Oikos, 2001, vol. 92, pp. 265–270.

    Article  Google Scholar 

  25. Beverton, R.J. and Holt, S.J., On the Dynamics of the Exploited Fish Populations, Great Brit. Min. Agr. Fish, Food, Fish. Invest., 1957, Ser. 2–19, pp. 1–533.

  26. Dellucchi, V., Parasitoids and Hyperparasitoids of Zeiraphera Diniana (Lepidoptera tortricidae) and Their Role in Population Control in Outbreak Areas, Entomophaga, 1982, vol. 27, pp. 77–92.

    Article  Google Scholar 

  27. Edelstein-Keshet, L. and Rausher, M.D., The Effects of Inducible Plant Defenses on Herbivore Populations. 1. Mobile Herbivores in Continuous Time, Am. Natur., 1989, vol. 133, pp. 787–810.

    Article  Google Scholar 

  28. Fischlin, A. and Baltensweiler, W., Systems Analysis of the Larch Bud Moth System. Part 1: The Larch-Larch Bud Moth Relationship, Bulletin de la Societe Entomologique Suisse, 1979, vol. 52, pp. 273–289.

    Google Scholar 

  29. Ginzburg, L.R. and Taneyhill, D.E., Population Cycles of Forest Lepidoptera: A Maternal Effect Hypothesis, Okeanologiya, 1994, vol. 63, pp. 79–92.

    Google Scholar 

  30. Hassell, M.P., Density-Dependence in Single-Species Populations, Okeanologiya, 1975, vol. 44, pp. 283–295.

    Google Scholar 

  31. Hilborn, R. and Mangel, M., The Ecological Detective, Princeton, New Jersey: Princeton Univ. Press, 1997.

    Google Scholar 

  32. Hunter, M.D. and Price, P.W., Cycles in Insect Populations: Delayed Density Dependence or Exogenous Driving Variables?, Ecol. Entomol., 1998, vol. 23, pp. 216–222.

    Article  Google Scholar 

  33. Kendall, B.E., Briggs, C.J., Murdoch, W.W., Turchin, P.., Ellner, S.P.., McCauley, E., Nisbet, R.M., and Wood, S.N., Why Do Population Cycle? A Synthesis of Statistical and Mechanistic Modeling Approaches, Ecology, 1999, vol. 80, pp. 1789–1805.

    Article  Google Scholar 

  34. Kostitzin, V.A., La Biologie Mathematique, Paris: A. Colin, 1937.

    Google Scholar 

  35. May, R.M., Biological Populations Obeying Difference Equations: Stable Points, Stable Cycles and Chaos, J. Theor. Biol., 1975, vol. 51, no. 2, pp. 511–524.

    Article  PubMed  CAS  Google Scholar 

  36. Maynard, SmithJ. and Slatkin, M., The Stability of Predator-Prey Systems, Ecology, 1973, vol. 54, pp. 384–391.

    Article  Google Scholar 

  37. Moran, P.A.P., Some Remarks on Animal Population Dynamics, Biometrics, 1950, vol. 6, no. 3, pp. 250–258.

    Article  PubMed  CAS  Google Scholar 

  38. Morris, R.F., Single-Factor Analysis in Population Dynamics, Ecology, 1959, vol. 40, pp. 580–588.

    Article  Google Scholar 

  39. Nedorezov, L.V., Escape-Effect and Population Outbreaks, Ecol. Model., 1997, vol. 94, pp. 95–110.

    Article  Google Scholar 

  40. Nedorezov, L.V., Lohr, B.L., and Sadykova, D.L., Assessing the Importance of Self-Regulating Mechanisms in Diamondback Moth Population Dynamics: Application of Discrete Mathematical Models, J. Theor. Biol., 2008, vol. 254, pp. 587–593.

    Article  PubMed  Google Scholar 

  41. NERC Centre for Population Biology The Global Population Dynamics Database, 1999. http://www3.imperial.ac.uk/cpb/research/patternsandprocesses/gpdd

  42. Ricker, W.E., Stock and Recruitment, J. Fish. Res. Board Canada, 1954, vol. 11, no. 5, pp. 559–623.

    Article  Google Scholar 

  43. Royama, T., Fundamental Concepts and Methodology for the Analysis of Animal Population Dynamics, with Particular Reference to Univoltine Species, Ecol. Monogr., 1981, vol. 51, pp. 473–493.

    Article  Google Scholar 

  44. Shapiro, S.S., Wilk, M.B., and Chen, H.J., A Comparative Study of Various Tests of Normality, J. Amer. Stat. Assoc., 1968, vol. 63, pp. 1343–1372.

    Article  Google Scholar 

  45. Skellam, J.G., Random Dispersal in Theoretical Populations, Biometrika, 1951, vol. 38, pp. 196–218.

    PubMed  CAS  Google Scholar 

  46. Tonnang, H., Nedorezov, L.V., Owino, J., Ochanda, H., and Lohr, B., Evaluation of Discrete Host-Parasitoid Models for Diamondback Moth and Diadegma semiclausum Field Time Population Density Series, Ecol. Model., 2009a, vol. 220, pp. 1735–1744.

    Article  Google Scholar 

  47. Tonnang, H., Nedorezov, L.V., Ochanda, H., Owino, J., and Lohr, B., Assessing the Impact of Biological Control of Plutella xylostella through the Application of Lotka-Volterra Model, Ecol. Model., 2009b, vol. 220, pp. 60–70.

    Article  Google Scholar 

  48. Turchin, P., Rarity of Density Dependence or Population Regulation with Lags?, Nature, 1990, vol. 344, pp. 660–663.

    Article  Google Scholar 

  49. Turchin, P., Complex Population Dynamics: A Theoretical/Empirical Synthesis, Princeton: Princeton Univ. Press, 2003.

    Google Scholar 

  50. Turchin, P.., Wood, S.N., Ellner, S.P., Kendall, B.E., Murdoch, W.W., Fischlin, A., Casas, J., McCauley, E., and Briggs, C.J., Dynamical Effects of Plant Quality and Parasitism on Population Cycles of Larch Budmoth, Ecology, 2003, vol. 84, no. 5, pp. 1207–1214.

    Article  Google Scholar 

  51. Varley, G.C. and Gradwell, G.R., Key Factors in Population Studies, Okeanologiya, 1960, vol. 29, pp. 399–401.

    Google Scholar 

  52. Varley, G.C. and Gradwell, G.R., Recent Advances in Insect Population Dynamics, Ann. Rev. Ent., 1970, vol. 15, pp. 1–24.

    Article  Google Scholar 

  53. Wood, S.N., Minimizing Model Fitting Objectives That Contain Spurious Local Minima by Bootstrap Restarting, Biometrics, 2001a, vol. 57, pp. 240–244.

    Article  PubMed  CAS  Google Scholar 

  54. Wood, S.N., Partially Specified Ecological Models, Ecol. Monogr., 2001b, vol. 71, pp. 1–25.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. The Research Center for Interdisciplinary Environmental Cooperation (INENCO) of Russian Academy of Sciences, Kutuzova nad. 14, St. Peterburg, 191187, Russia

    L. V. Nedorezov

Authors
  1. L. V. Nedorezov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. V. Nedorezov.

Additional information

Original Russian Text © L.V. Nedorezov, 2011, published in Zhurnal Obshchei Biologii, 2011, Vol. 72, No. 2, pp. 83–92.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nedorezov, L.V. Analysis of cyclic fluctuations in larch bud moth populations with discrete-time dynamic models. Biol Bull Rev 1, 407–414 (2011). https://doi.org/10.1134/S2079086411050057

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S2079086411050057

Keywords

Search

Navigation