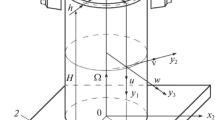
Abstract
A new mathematical model of wave solid-state gyro is constructed, which describes interrelated electrical and mechanical oscillations in the case when the voltage is available at the electrodes. Wave pattern of resonator oscillations was studied using asymptotic Krylov-Bogoliubov method. Nonlinear electric processes in resonator control loop lead to additional gyro errors. A numerical example is provided.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Peshekhonov, V.G., Gyros of the early 21st century, Giroskopiya i Navigatsiya, 2003, no. 4, pp. 5–18.
Matveev, V.A., Lunin, B.S., and Basarab, M.A., Navi-gatsionnye sistemy na volnovykh tverdotel’nykh giroskopakh (Navigation Systems of Wave Solid-State Gyros), Moscow: Fizmatlit, 2008.
Zhuravlev, V.F. and Klimov, D.M., Volnovoi tverdotel’nyi giroskop (Wave Solid-State Gyroscope), Moscow: Nauka, 1985.
Maslov, A.A., Maslov, D.A., and Merkuryev, I.V., Studying stationary oscillation modes of the gyro resonator in the presence of positional and parametric excitations, Gyroscopy and Navigation, 2014, vol. 5, no. 4, pp. 224–228.
Zhuravlev, V.F. and Lynch D.D., Electrical model of the wave solid-state gyroscope, Izv. RAN MTT, 1995, no. 5, pp. 12–24.
Sudipto, K. De. and Aluru, N.R., Complex nonlinear oscillations in electrostatically actuated microstruc-tures, J. Microelectromech. Syst., 2006, vol. 15, no. 2, pp. 355–369.
Rhoads, J., Shaw, S., Tunner, K., Moehlis, J., DeMartini, B., Zhang, W., Generalized parametric reso-nance in electrostatically actuated microelectrome-chanical oscillators, J. Sound and Vib., 2006, vol. 296, pp. 797–829.
Chavarett, F.R., Balthaza, I.M., Guilherm, I.R. and Nasciment, O.S., A reducing of chaotic behavior to a periodic orbit, of a combdriver drive system (MEMS) using particle swarm optimization, Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications, Serra Negra, 2010, pp. 378–383.
Merkuryev, I.V. and Podalkov, V.V., Dinamika mik-romekhanicheskogo i volnovogo tverdotel’nogo girosk-opov (Dynamics of the Micromechanical and Wave Solid-State Gyroscopes), Moscow: Fizmatlit, 2009.
Zhurvalev, V.F., Controlled Faucault pendulum as a model of a class of free gyros, Izv. RAN. MTT, 1997, no. 6, pp. 27–35.
Maslov, A.A., Maslov, D.A., Merkuryev, I.V., and Mikhailov, D.V., Drift of wave solid-state gyro in the presence of reference voltage on control electrodes, Vestnik MEI, 2013, no. 2, pp. 11–14.
RF Patent 2056038, Hemispherical resonator made of quartz glass within wave solid-state gyro, Lunin, B.S., Pavlov, I.V., 1996.
RF Patent 2544308, A method of characterization of wave solid-state gyro, Maslov, A.A., Merkuryev, I.V., and Maslov, D.A., 2015.
Maslov, A.A., Maslov, D.A., and Merkuryev, I.V., Iden-tification of parameters of wave solid-state gyro with account for nonlinear resonator oscillations, Pribory i Sistemy. Upravlenie, Kontrol’, Diagnostika, 2014, no. 5, pp. 18–23.
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Giroskopiya i Navigatsiya, 2015, No. 1, pp. 71–80.
Rights and permissions
About this article
Cite this article
Maslov, A.A., Maslov, D.A. & Merkuryev, I.V. Nonlinear effects in dynamics of cylindrical resonator of wave solid-state gyro with electrostatic control system. Gyroscopy Navig. 6, 224–229 (2015). https://doi.org/10.1134/S2075108715030104
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S2075108715030104