Skip to main content
SpringerLink
Log in

Multirate Solver with Speed and Gap Control

  • Published:
Mathematical Models and Computer Simulations Aims and scope

Abstract—

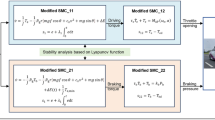
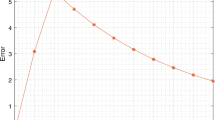
Computer simulation of vehicular traffic on the real road network can be used to solve a whole range of relevant and practical problems. The microscopic approach and tens of thousands of vehicles used in simulation lead to large systems of ordinary differential equations. The vehicle dynamics can vary significantly. As a result, the corresponding systems of differential equations have a certain feature, i.e., the rate of change in unknown vector components, which in this case are the speeds of vehicles and the distances (gaps) between them, varies significantly. In this paper, we propose a multirate numerical integration scheme, in which an individual microstep is used for each component of the vector of unknowns within each macrostep. The values of the steps are determined using the obtained local error estimate of the given numerical scheme. The corresponding time-stepping strategy is obtained both for vehicle speeds and for distances between vehicles. Moreover, the multirate solver’s local error for gaps is estimated one order of accuracy higher than for speeds because drivers estimate the gap primarily rather than the speed. The developed numerical method shows a significant computational speedup in comparison with the corresponding single-rate method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

REFERENCES

  1. M. Treiber and A. Kesting, Traffic Flow Dynamics (Springer, Berlin, 2013).

    Book  MATH  Google Scholar 

  2. A. V. Gasnikov, Introduction to Mathematical Modeling of Traffic Flows (MFTI, Moscow, 2010) [in Russian].

    Google Scholar 

  3. G. Orosz, R. E. Wilson, and B. Krauskopf, “Global bifurcation investigation of an optimal velocity traffic model with driver reaction time,” Phys. Rev. E 70, 026207 (2004).

    Article  MathSciNet  Google Scholar 

  4. A. Tordeux, S. Lassarre and M. Roussignol, “An adaptive time gap car-following model,” Transp. Res., Part B 44, 1115–1131 (2010).

    Article  Google Scholar 

  5. C. Gear and D. Wells, “Multirate linear multistep methods,” BIT 24, 484–502 (1984).

    Article  MathSciNet  MATH  Google Scholar 

  6. M. Gunther, A. Kværnø, and P. Rentrop, “Multirate partitioned Runge-Kutta methods,” BIT 41, 504–514 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  7. V. Savcenco, W. Hundsdorfer, and J. G. Verwer, “A multirate time stepping strategy for stiff ordinary differential equations,” BIT 47, 137–155 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  8. A. B. Korchak and A. V. Evdokimov, “The method of parallel calculation of split systems of differential equations with multiple steps,” Tr. MFTI 2 (2), 77–85 (2010).

    Google Scholar 

  9. V. V. Kurtc and I. E. Anufriev, “Multirate numerical scheme for large-scale vehicle traffic simulation,” Math. Models Comput. Simul. 8, 744–751 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  10. H. J. Payne, “Models of freeway traffic and control,” in Mathematical Models of Public Systems, Ed. by G. A. Bekey (Simulation Council, 1971), Vol. 1, pp. 51–61.

    Google Scholar 

  11. B. S. Kerner and P. Konhauser, “Cluster effect in initially homogeneous traffic flow,” Phys. Rev. E 48, 2335–2338 (1993).

    Article  Google Scholar 

  12. A. A. Chechina, N. G. Churbanova and M. A. Trapeznikova, “Two-dimensional hydrodynamic model for traffic flow simulation using parallel computer systems,” in Proceedings of the International Conference of the Numerical Analysis and Applied Mathematics 2014, AIP Conf. Proc. 1648, 530007 (2015).

  13. R. Jiang, Q. Wu, and Z. Zhu, “Full velocity difference model for a car-following theory,” Phys. Rev. E 64, 017101-1–017101-4 (2001).

    Article  Google Scholar 

  14. M. Treiber, A. Kesting, and D. Helbing, “Delays, inaccuracies and anticipation in microscopic traffic models,” Phys. A (Amsterdam, Neth.) 360, 71–88 (2006).

  15. I. Lubashevsky, P. Wagner, and R. Manhke, “A bounded rational driver model,” Eur. Phys. J. B 32, 243–247 (2003).

    Article  Google Scholar 

  16. A. Kværnø, “Stability of multirate Runge-Kutta schemes,” Int. J. Differ. Equ. Appl. 1A, 97–105 (2000).

    MathSciNet  MATH  Google Scholar 

  17. S. Skelboe, “Stability properties of backward differentiation multirate formulas,” Appl. Numer. Math. 5, 151–160 (1989).

    Article  MathSciNet  MATH  Google Scholar 

  18. A. Verhoeven et al., “Stability analysis of the BDF slowest first multirate methods,” CASA-Report No. 0704, Int. J. Comput. Math. 84, 895–923 (2006).

    Article  MathSciNet  Google Scholar 

  19. V. Kurtc and I. Anufriev, “Local stability conditions and calibrating procedure for new car-following models used in driving simulators,” in Proceedings of the 10th Conference on Traffic and Granular Flow'13, 2015, pp. 453–461.

Download references

Author information

Authors and Affiliations

  1. Peter the Great St. Petersburg Polytechnic University, St. Petersburg, Russia

    V. V. Kurtc & I. E. Anufriev

Authors
  1. V. V. Kurtc
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. E. Anufriev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. V. Kurtc.

Additional information

Translated by O. Pismenov

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kurtc, V.V., Anufriev, I.E. Multirate Solver with Speed and Gap Control. Math Models Comput Simul 11, 386–392 (2019). https://doi.org/10.1134/S207004821903013X

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S207004821903013X

Keywords:

Search

Navigation