Skip to main content
SpringerLink
Log in

Numerical Simulation of a Hypersonic Flow over an Aircraft in a High-Altitude Active Movement Area

  • Published:
Mathematical Models and Computer Simulations Aims and scope

Abstract

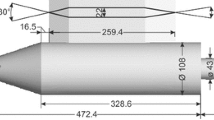
A hypersonic flow over an axisymmetric aircraft is numerically simulated in the case of a highly underexpanded exhaust plume (jet) of the main engine. The characteristics of the boundary layer separation occurring on the aircraft’s side surface are investigated for several successive points of its takeoff path. The Mach number at the nozzle exit is 6.5. The Mach number of the incoming flow varies from 4 to 7. In this case, the Reynolds number ranges from 2.5 × 105 to 3 × 103 and the ratio of the nozzle’s exit pressure to the ambient pressure, from 350 to 5 × 104. In the case of the Mach number of the incoming flow M∞ = 4, the variation range of the pressure ratio extends to 106. Replacement of the exhaust plume with a rigid simulator is considered. Data are obtained on the pressure ratios for which a separation flow begins to form on the side surface, the recirculation zone length, and the level of pressure in it in comparison with the available empirical dependences. A significant increase of the recirculation zone in front of the exhaust plume is shown when it is replaced by a rigid simulator of the same dimensions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. Carriere and M. Serieix, “Effects aerodynamique de l’eclament d’un jet de fusee,” Rech. Aerosp., No. 89, 3–30 (1962).

    Google Scholar 

  2. R. Adams, “Wind tunnel testing tecniques for gas-particle flows in rocket exhaust plumes,” AIAA Paper N66-767 (AIAA, 1966).

    Google Scholar 

  3. L. Alpinieri and R. Adams, “Flow separation due to jet pluming,” AIAA J. 4, 1865–1866 (1966).

    Article  Google Scholar 

  4. W. F. Hinson and R. J. McGhee, “Effects of jet pluming on the static stability of five rocket models at Mach numbers of 4, 5, and 6 and static pressure rations up to 26000,” NASA TN D-4064 (1967).

    Google Scholar 

  5. R. C. Boger, H. Rosenbaum, and B. L. Reeves, “Flow field interactions induced by underexpanded exhaust plumes,” AIAA J. 10, 300–306 (1972).

    Article  Google Scholar 

  6. A. N. Shliagun, “Interaction of strongly underexpanded supersonic jet with a hypersonic sputtered flow,” Uch. Zap. TsAGI 10 (3), 37–47 (1979).

    Google Scholar 

  7. J. M. Klineberg, T. Kubota, and L. Lees, “Theory of exhaust-plumes/boundary-layer interactions at supersonic speeds,” AIAA J. 10, 581–588 (1972).

    Article  Google Scholar 

  8. P. K. Chang, Separation of Flow (Pergamon, Oxford, New York, 1970).

    MATH  Google Scholar 

  9. J. Erdos and A. Pallone, “Shock-boundary layer interactoin and flow separation,” Proc. Heat Transfer Fluid Mech. Inst., 239–254 (1962).

    Google Scholar 

  10. K. J. Plotkin and J. S. Draper, “Detachment of the outer shock from underexpanded rocket plumes,” AIAA J. 10, 1707–1709 (1972).

    Article  Google Scholar 

  11. E. V. Myshenkov and V. I. Myshrnkov, “Regimes of laminar flow separation due to jet exhaust,” Fluid Dyn. 29, 103–107 (1994).

    Article  Google Scholar 

  12. E. V. Myshenkov and V. I. Myshrnkov, “Formation of lateral separation caused by a sustainer engine jet,” Fluid Dyn. 30, 592–598 (1995).

    Article  Google Scholar 

  13. L. G. Loytsyansky, Mechanics of Liquids and Gases (Pergamon, Oxford, 1966; Nauka, Moscow, 1987).

    Google Scholar 

  14. F. R. Menter, “Zonal two equation κ-ω turbulence models for aerodynamic flows,” AIAA Paper 93-2906 (AIAA, 1993).

    Google Scholar 

  15. J. L. Steger, “Implicit finite-difference simulation of flow about arbitrary two-dimensional geometries,” AIAA J. 16, 679–686 (1978).

    Article  MATH  Google Scholar 

  16. A. D. Savel’ev, “The use of high order composite compact schemes for computing supersonic jet interaction with a surface,” Comput. Math. Math. Phys. 53, 1558–1570 (2013).

    Article  MathSciNet  MATH  Google Scholar 

  17. M. N. Mikhailovskaya and B. V. Rogov, “Monotone compact running schemes for systems of hyperbolic equatins,” Comput. Math. Math. Phys. 52, 578–600 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  18. S. K. Lele, “Compact finite difference schemes with spectral-like resolution,” J. Comput. Phys. 102, 16–42 (1992).

    Article  MathSciNet  MATH  Google Scholar 

  19. A. D. Savel’ev, “On the structure of internal dissipation of composite compact schemes for gasdynamic simulation,” Comput. Math. Math. Phys. 49, 2135–2148 (2009).

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dorodnicyn Computing Centre, Russian Academy of Sciences, Moscow, Russia

    A. D. Savel’ev

Authors
  1. A. D. Savel’ev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. D. Savel’ev.

Additional information

Original Russian Text © A.D. Savel’ev, 2017, published in Matematicheskoe Modelirovanie, 2017, Vol. 29, No. 9, pp. 90–100.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Savel’ev, A.D. Numerical Simulation of a Hypersonic Flow over an Aircraft in a High-Altitude Active Movement Area. Math Models Comput Simul 10, 218–225 (2018). https://doi.org/10.1134/S2070048218020114

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S2070048218020114

Keywords

Search

Navigation