Abstract
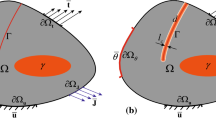
A mathematical model and numerical method for simulation of the continuous casting process in a variable in time domain are presented. The variable geometry of the slab is caused by the change in time of the width of the mould. The mathematical model of the process is a Stefan problem with prescribed convection and non-linear Robin boundary condition. Considered differential equation is approximated by a finite difference scheme, which is constructed in several steps. First, a semi-discrete problem is constructed using the method of characteristics with respect to the time variable. Then, at each time level, the current elliptic problem in a curvilinear domain is replaced by a problem in the parallelepiped domain using the fictitious domain method. Finally, the boundary-value problem in the parallelepiped domain is approximated by a finite-difference scheme. The constructed fully discrete problem in algebraic form is a system of nonlinear equations containing a diagonal monotone operator and a linear part with a symmetric and positive definite \(M\)-matrix. To solve the resulting system of nonlinear algebraic equations, well-known iterative solution methods can be applied.


Similar content being viewed by others
REFERENCES
S. Louhenkilpi, E. Laitinen, and R. Nieminen, ‘‘Real time transfer in simulation of heat continuous casting,’’ Metall. Trans., B 24, 685–693 (1993).
S. K. Choudhary, D. Mazumdar, and A. Ghosh, ‘‘Mathematical modelling of heat transfer phenomena in continuous casting of steel,’’ ISIJ Int. 33, 764–774 (1993).
S. Louhenkilpi et al., ‘‘Online modelling of heat transfer, solidification and microstructure in continuous casting of steel,’’ IOP Conf. Ser.: Mater. Sci. Eng. 529 (2019).
S. Kittaka, T. Kanki, K. Watanabe, and Ya. Miura, ‘‘Nippon steel high speed variable width mould NS-VWM for slab caster,’’ Tech. Report No. 86 (Nippon Steel Corp., Chiba, Japan, 2002), pp. 74–79.
Md Obaidullah Ansari, Joyjeet Ghose, and Rajshree Samantray, ‘‘Automatic mould width adjustments system of slab caster during casting,’’ Discovery 45 (209), 127–131 (2015).
Z. Chen, ‘‘Numerical solutions of a two-phase continuous casting problem,’’ in Numerical Methods for Free Boundary Problems, Ed. by P. Neittaanmäki, Int. Ser. Numer. Math. 99, 103–121 (1991).
Z. Chen, and L. Jiang, ‘‘Approximation of a two-phase continuous casting problem,’’ J. Partial Differ. Equat. 11, 59–72 (1998).
Z. Chen, T. Shih, and X. Yue, ‘‘Numerical methods for Stefan problems with prescribed convection and nonlinear flux,’’ IMA J. Numer. Anal. 20, 81–98 (2000).
E. Laitinen, A. Lapin, and J. Pieskä, ‘‘Mesh approximation and iterative solution of the continuous casting problem,’’ in ENUMATH 99—Proceeding of the 3rd European Conference on Numerical Mathematics and Advanced Applications, Ed. by P. Neittaanmäki, T. Tiihonen, and P. Tarvainen (World Scientific, Singapore, 2000), pp. 601–617.
E. Laitinen and J. Pieskä, ‘‘Comparison of upwind and characteristic schemes for solving multiphase diffusion-convection equation,’’Comput. Assist. Mech. Eng. Sci. 7, 421–426 (2000).
E. Laitinen, A. V. Lapin, and J. Pieska, ‘‘Large splitting iterative methods and parallel solution of variational inequalities,’’ Lobachevskii J. Math. 8, 167–184 (2001).
E. Laitinen, A. V. Lapin, and J. Pieska, ‘‘Asynchronous domain decomposition methods for continuous casting problem,’’ J. Comput. Appl. Math. 154, 393–413 (2003).
K. Milkowska-Piszczek and Jan Falkus, ‘‘Control and design of the steel continuous casting process based on advanced numerical models,’’ Metals 8 (2018).
S. Del Pino and O. Pironneau, ‘‘A fictitious domain based general PDE solver,’’ in Numerical Methods for Scientific Computing, Variational Problems and Applications, Ed. by Y. Kuznetsov, P. Neittanmaki, and O. Pironneau (CIMNE, Barcelona, 2003).
Ph. Angot, ‘‘A unified fictitious domain model for general embedded boundary conditions,’’ C. R. Math. 341, 683–688 (2005).
Sheng Zhang, ‘‘A domain embedding method for mixed boundary value problems,’’ C. R. Acad. Sci. Paris, Ser. I 343, 287–290 (2006).
I. Ramiere, Ph. Angot, and M. Belliard, ‘‘Fictitious domain methods to solve convection-diffusion problems with general boundary conditions,’’ in Proceedings of the 17th Computational Fluid Dynamics Conference-AIAA, AIAA 2005-4709 (Toronto, Canada, 2005).
I. Ramiere, Ph. Angot, and M. Belliard, ‘‘A general fictitious domain method with immersed jumps and multilevel nested structured meshes,’’ J. Comput. Phys. 225, 1347–1387 (2007).
J. Rulla, ‘‘Weak solutions to Stefan problems with prescribed convection,’’ SIAM J. Math. Anal. 18, 1784–1800 (1987).
J. F Rodrigues and F. Yi, ‘‘On a two-phase continuous casting Stefan problem with nonlinear flux,’’ Eur. J. App. Math. 1, 259–278 (1990).
J. Douglas, Jr. and T. F. Russel, ‘‘Numerical methods for convection-dominated diffusion problem based on combining the method of characteristic with finite element or finite difference procedures,’’ SIAM J. Numer. Anal. 19, 871–885 (1982).
J.-L. Lions, Quelques méthodes de résolution des problèmes aux limites non linéaires (Dunod, Paris, 1969).
Ph. J. Ciarlet, The Finite Element Method for Elliptic Problems (SIAM, Philadelphia, 2002).
J. M. Ortega and W. C. Rheinboldt, Iterative Solution of Nonlinear Equations in Several Variables (SIAM, Philadelphia, 1987).
Funding
This research was supported by Academy of Finland, grant No. 333448 (Alexander Lapin) and no. 333551 (Erkki Laitinen).
Author information
Authors and Affiliations
Corresponding authors
Additional information
(Submitted by A. M. Elizarov)
Rights and permissions
About this article
Cite this article
Lapin, A., Laitinen, E. A Numerical Model for Steel Continuous Casting Problem in a Time-variable Domain. Lobachevskii J Math 41, 2664–2672 (2020). https://doi.org/10.1134/S1995080220120239
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1995080220120239