Abstract
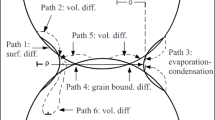
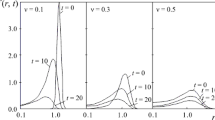
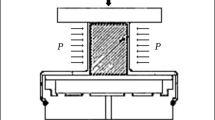
On the basis of a physical model of sintering, a numerical analysis of the temporal form change in the simulative powder compacts from particles with various distribution widths is carried out. It is shown that, provided the average particle size and initial density of packing are the same, the average grains size in the sintered material and the grains size distribution width both increase with growth of particle-distribution width. The best results from the point of view of productivity of the process (time of sintering) and the qualities of the final product (the average size of the grain) are demonstrated by monodisperse powders. The pro-posed numerical technique may be useful for a qualitative analysis of sintering of the powder compacts, for the reason to optimize the technological parameters and the quality of the material.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
G. Deresevich, “Mechanics of a Granular Media,” in Problems of Mechanics (Inostr. Liter., Moscow, 1961) [in Russian].
N. Das and H. S. Maiti, “Effect of Size Distribution of the Starting Powders on the Pore Size and its Distribution of Tape Cast Alumina Microporous Membranes,” J. Eur. Ceram. Soc. 19, 341 (1999).
R. L. Coble, “Effects of Particle-Size Distribution in Initial-Stage Sintering,” J. Am. Ceram. Soc. 56(9), 461 (1993).
F. Wakai, M. Yoshida, and B. P. Kashyap, “Influence of Particle Arrangement on Coarsening during Sintering of Free Spherical Particles,” J. Ceram. Soc. Jpn. 114(11), 974 (2006).
A. V. Galakhov, “Pore Coordination Number and Sintering,” Refract. Industr. Ceram. 51, 83–87 (2010).
A. V. Galakhov and V. Ya. Shevchenko, “Analysis of Two-Dimensional Packing, Refractories 32, 629 (1991).
C. A. Brebbia, The Boundary Element Method for Engineers (Wiley, New York, 1978; Mir, Moscow, 1982).
A. V. Galakhov, “Numerical Methods of Simulating Sintering,” Refract. Industr. Ceram. 50, 191 (2009).
Ya. E. Geguzin, Physics of Sintering (Nauka, Moscow, 1984) [in Russian].
S. S. Gorelik, S. V. Dobatkin, and L. Kaputkina, Recrystallization of Metals and Alloys (MISIS, Moscow, 2005) [in Russian].
J. Hirth and J. Lotte, Theory of Dislocations (McGraw-Hill, New York, 1967; Atomizdat, Moscow, 1972).
J. M. Dynys, R. L. Coble, and W. S. Coblenz, “Mechanisms of Atom Transport during Initial Stage Sintering of Al2O3,” Mat. Sci. Res. 13, 391 (1979).
P. Nicolopoulus, “Surface, Grain-Boundary and Interfacial Energies in Al2O3 and Al2O3-Sn, Al2O3-Co Systems,” J. Mat. Sci. 20, 3993 (1985).
A. B. Nandiyanto and K. Okuyama, “Progress in Developing Spray-Drying Methods for the Production of Controlled Morphology Particles: From the Nanometer to Submicrometer Size Range,” Adv. Powder Technol. 22, 1 (2011).
A. V. Galakhov, L. V. Vinogradov, V. I. Antipov, and A. G. Kolmakov, “Nanostructured Powders for Ceramics,” Nanotechnol. Russia 6, 662 (2011).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © A.V. Galakhov, 2012, published in Rossiiskie Nanotekhnologii, 2012, Vol. 7, Nos. 1–2.
Rights and permissions
About this article
Cite this article
Galakhov, A.V. Distribution of particles in sizes and sintering: A numerical analysis. Nanotechnol Russia 7, 54–61 (2012). https://doi.org/10.1134/S1995078012010065
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1995078012010065