Abstract
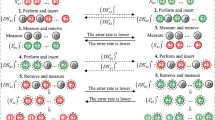
We present a protocol for perfectly teleporting a five-qubit state of specific type. We utilize a sixqubit entangled quantum channel for this purpose. In this protocol only four out of 26 possible measurement outcomes appear. This leads to a substantial convenience in the implementation of the protocol.
Similar content being viewed by others
References
C. H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. K. Wootters, “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels,” Phys. Rev. Lett. 70, 1895–1899 (1993).
W. L. Li, C. F. Li, and G. C. Guo, “Probabilistic teleportation and entanglement matching,” Phys. Rev. A 61, 034301 (2000).
B. S. Shi, Y. K. Jiang, and G. C. Guo, “Probabilistic teleportation of two-particle entangled state,” Phys. Lett. A 268, 161–164 (2000).
P. Agrawal and A. K. Pati, “Probabilistic quantum teleportation,” Phys. Lett. A 305, 12–17 (2002).
F. Yan and D. Wang, “Probabilistic and controlled teleportation of unknown quantum states,” Phys. Lett. A 316, 297–303 (2003).
L. Z. Yu and T. Wu, “Probabilistic teleportation of three-qubit entangled state via five-qubit cluster state,” Int. J. Theor. Phys. 52, 1461–1465 (2013).
H. F. Hofmann, T. Ide, T. Kobayashi, and A. Furusawa, “Fidelity and information in the quantum teleportation of continuous variables,” Phys. Rev. A 62, 062304 (2000).
S. Oh, S. Lee, and H. W. Lee, “Fidelity of quantum teleportation through noisy channels,” Phys. Rev. A 66, 022316 (2002).
G. Li, M. Y. Ye, and X. M. Lin, “Entanglement fidelity of the standard quantum teleportation channel,” Phys. Lett. A 377, 1531–1533 (2013).
C. H. Bennett, G. Brassard, S. Popescu, B. Schumacher, J. A. Smolin, and W. K. Wootters, “Purification of noisy entanglement and faithful teleportation via noisy channels,” Phys. Rev. Lett. 76, 722 (1996).
P. Espoukeh and P. Pedram, “Quantum teleportation through noisy channels with multi-qubit GHZ states,” Quantum Inf. Process. 13, 1789 (2014).
L. T. Knoll, C. T. Schmiegelow, and M. A. Larotonda, “Noisy quantum teleportation: an experimental study on the influence of local environments,” Phys. Rev. A 90, 042332 (2014).
L. Vaidman, “Teleportation of quantum states,” Phys. Rev. A 49, 1473–1476 (1994).
Y. H. Kim, S. P. Kulik, and Y. Shih, “Quantum teleportation of a polarization state with a complete bell state measurement,” Phys. Rev. Lett. 86, 1370 (2001).
M. D. Barrett, J. Chiaverini, T. Schaetz, J. Britton, W. M. Itano, J. D. Jost, E. Knill, C. Langer, D. Leibfried, R. Ozeri, and D. J. Wineland, “Deterministic quantum teleportation of atomic qubits,” Nature 429, 737 (2004).
S. B. Zheng, “Scheme for approximate conditional teleportation of an unknown atomic state without the bell-state measurement,” Phys. Rev. A 69, 064302 (2004).
F. L. Yan and X. Q. Zhang, “A scheme for secure direct communication using EPR pairs and teleportation,” Eur. Phys. J. B 41, 7578 (2004).
T. Gao, F. L. Yan, and Z. X. Wang, “Controlled quantum teleportation and secure direct communication,” Chin. Phys. 14, 893–897 (2005).
G. Rigolin, “Quantum teleportation of an arbitrary two qubit state and its relation to multipartite entanglement,” Phys. Rev. A 71, 032303 (2005).
H. J. Cao and H. S. Song, “Quantum secure direct communication scheme using a W state and teleportation,” Phys. Scr. 74, 572 (2006).
C. W. Tsai and T. Hwang, “Teleportation of a pure EPR state via GHZ-like state,” Int. J. Theor. Phys. 49, 1969–1975 (2010).
Q. Shao, “Quantum teleportation of the two-qubit entangled state by use of four-qubit entangled state,” Int. J. Theor. Phys. 52, 2573–2577 (2013).
H. P. Zhu, “Perfect teleportation of an arbitrary twoqubit state via GHZ-like states,” Int. J. Theor. Phys. 53, 4095–4097 (2014).
Y. Y. Nie, Y. H. Li, C. P. Jin, J. C. Liu, and M. H. Sang, “Quantum information splitting of an arbitrary multiqubit GHZ-type state by using a four-qubit cluster state,” Int. J. Theor. Phys. 50, 2799 (2011).
Y. H. Li, X. L. Li, L. P. Nie, and M. H. Sang, “Quantum teleportation of three and four-qubit state using multi-qubit cluster states,” Int. J. Theor. Phys. 55, 1820–1823 (2016).
B. S. Choudhury and A. Dhara, “Teleportation protocol of three-qubit state using four-qubit quantum channels,” Int. J. Theor. Phys. doi 10.1007/s10773-016-2967-1
Y. H. Li, M. H. Sang, X. P. Wang, and Y. Y. Nie, “Quantum teleportation of a four-qubit state by using six-qubit cluster state,” Int. J. Theor. Phys. doi 10.1007/s10773-016-2982-2
B. Zhang, T. X. Liu, and J. Wang, “Quantum teleportation of an arbitrary n-qubit state via GHZ-like states,” Int. J. Theor. Phys. 55, 1601–1611 (2016).
Author information
Authors and Affiliations
Corresponding author
Additional information
The article is published in the original.
Rights and permissions
About this article
Cite this article
Choudhury, B.S., Dhara, A. & Samanta, S. Teleportation of five-qubit state using six-qubit state. Phys. Part. Nuclei Lett. 14, 644–646 (2017). https://doi.org/10.1134/S1547477117040069
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1547477117040069