Skip to main content
SpringerLink
Log in

Azimuthal pion fluctuation in ultra relativistic nuclear collisions and centrality dependence—a study with chaos based complex network analysis

  • Physics of Elementary Particles and Atomic Nuclei. Experiment
  • Published:
Physics of Particles and Nuclei Letters Aims and scope Submit manuscript

Abstract

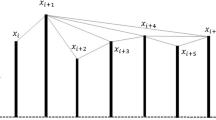
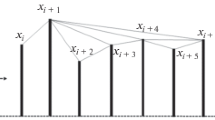
Various works on multiplicity fluctuation have investigated the dynamics of particle production process and eventually have tried to reveal a signature of phase transition in ultra-relativistic nuclear collisions. Analysis of fluctuations of spatial patterns has been conducted in terms of conventional approach. However, analysis with fractal dynamics on the scaling behavior of the void has not been explored yet. In this work we have attempted to analyze pion fluctuation in terms of the scaling behavior of the void probability distribution in azimuthal space in ultra-relativistic nuclear collisions in the light of complex networks. A radically different and rigorous method viz. Visibility Graph was applied on the data of 32S-Ag/Br interaction at an incident energy of 200 GeV per nucleon. The analysis reveals strong scaling behavior of void probability distributions in azimuthal space and a strong centrality dependence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. D. Ghosh, A. Deb, S. Bhattacharyya, J. G. R. Das, and S. Mukherjee, “Evidence of intermittent type fluctuation of target residue in relativistic nuclear collisions at a few GeV/N,” Int. J. Mod. Phys. E 12, 407–419 (2003).

    Article  ADS  Google Scholar 

  2. S. Sarkar, T. Goswami, D. Ghosh, and A. Deb, “Intermittency in the slow particle emission during hadron nucleus interactions,” Czechosl. J. Phys. 53, 133–141 (2003).

    Article  ADS  Google Scholar 

  3. A. Bialas and B. Ziaja, “Intermittency in a single event,” Phys. Lett. B 378, 319–322 (1996).

    Article  ADS  Google Scholar 

  4. D. Ghosh, P. Ghosh, A. Ghosh, and J. Roy, “Intermittency and fragmentation of target residue in highenergy nuclear interactions,” Phys. Rev. 49, R1747–R1750 (1994).

    ADS  Google Scholar 

  5. D. Ghosh, A. Deb, M. Lahiri, A. Dey, S. A. Hossain, S. Das, S. Sen, S. Halder, and J. Roy, “Multihadron production in high-energy interactions and intermittency,” Phys. Rev. D 49, 3113–3119 (1994).

    Article  ADS  Google Scholar 

  6. D. Ghosh, P. Ghosh, A. Ghosh, and J. Roy, “Nonstatistical fluctuations in fragmentation of target nuclei in high energy nuclear interactions,” J. Phys. G: Nucl. Part. Phys. 20, 1077–1082 (1994).

    Article  ADS  Google Scholar 

  7. D. Ghosh, A. K. Jafry, A. Deb, S. Sarkar, R. Chattopadhyay, and S. Das, “Multidimensional intermittency analysis in ultrarelativistic heavy ion interaction,” Phys. Rev. C 59, 2286–2288 (1999).

    Article  ADS  Google Scholar 

  8. “Factorial, multifractal moments and short-range correlation of shower particles at relativistic energies," Nucl. Phys. A 596, 700–712 (1996).

  9. D. Ghosh, J. Roy, M. Basu, K. Sengupta, S. Naha, A. Bhattacharyya, and T. G. Thakurta, “Rapidity-gap and rapidity-correlation study in 400-GeV/c protonnucleus interactions,” Phys. Rev. D 26, 2983–2990 (1982).

    Article  ADS  Google Scholar 

  10. D. Ghosh, K. Purkait, and R. Sengupta, “Correlation among target fragments in ‘hot’ and ‘cold’ events in relativistic heavy ion interaction,” Acta Phys. Slov. 47, 425–430 (1997).

    Google Scholar 

  11. D. Ghosh, A. Deb, S. Bhattacharyya, M. Mondol, R. Das, J. Ghosh, K. Chattopadhayay, R. Sarkar, S. Mukherjee, S. Biswas, et al., “Target fragmentation in 28Si-AgBr interactions at 14.5 AGeV-evidence for two-and many-particle dynamical correlations,” Fizika B (Zagreb) 11 (1/4), 73–82 (2002).

    ADS  Google Scholar 

  12. R. C. Hwa and Q.-h. Zhang, “Erraticity of rapidity gaps,” Phys. Rev. D 62, 014003 (2000).

    Article  ADS  Google Scholar 

  13. R. C. Hwa, “Fractal measures in multiparticle production,” Phys. Rev. D 41, 1456–1462 (1990).

    Article  ADS  Google Scholar 

  14. F. Takagi, “Multifractal structure of multiplicity distributions in particle collisions at high energies,” Phys. Rev. Lett. 72, 32–35 (1994).

    Article  ADS  Google Scholar 

  15. G. Paladin and A. Vulpiani, “Anomalous scaling laws in multifractal objects,” Phys. Rep. 156, 147–225 (1987).

    Article  ADS  MathSciNet  Google Scholar 

  16. P. Grassberger and I. Procaccia, “Dimensions and entropies of strange attractors from a fluctuating dynamics approach,” Phys. D: Nonlin. Phenom. 13, 34–54 (1984).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. T. C. Halsey, M. H. Jensen, L. P. Kadanoff, I. Procaccia, and B. I. Shraiman, “Fractal measures and their singularities: the characterization of strange sets,” Phys. Rev. A 33, 1141–1151 (1986).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. D. Ghosh, A. Mukhopadhyay, A. Ghosh, and J. Roy, “Zonal poissonian pion multiplicity in central 24Mg-AgBr collisions at Dubna energy,” Mod. Phys. Lett. A 04, 1197–1202 (1989).

    Article  ADS  Google Scholar 

  19. D. Ghosh, M. Lahiri, A. Deb, S. Das, K. Purkait, B. Biswas, J. Roychoudhury, R. Chatterjee, and A. K. Zafri, “Factorial correlator study in Ag32/Br interaction at 200A GeV,” Phys. Rev. C 52, 2092–2096 (1995).

    Article  ADS  Google Scholar 

  20. D. Ghosh, M. Momdal, A. Deb, and A. Ghosh, “Erractivity analysis of multipion data in 32A-AgBr interactions at 200A GeV,” Phys. Rev. D: Part. Fields 68, 024908 (2003).

    ADS  Google Scholar 

  21. D. Ghosh, P. Ghosh, A. Deb, and D. Halder, S. Das, A. Hossain, A. Dey, and J. Roy, “Self-similarity in particle production in hadron-nucleus interactions at 350 and 200 GeV/c,” Phys. Rev. D 46, 3712–3719 (1992).

    Article  ADS  Google Scholar 

  22. D. Ghosh, S. Sen, and J. Roy, “Maximum fluctuations of particle densities in narrow pseudorapidity space in high-energy interaction of hadrons with nuclei,” Phys. Rev. D 47, 1235–1238 (1993).

    Article  ADS  Google Scholar 

  23. D. Ghosh, A. Deb, S. R. Sahoo, and P. K. Haldar, “A study on azimuthal asymmetry of emission of pions produced in ultra-relativistic nuclear collisions,” Europhys. Lett. 56, 639–643 (2001).

    Article  ADS  Google Scholar 

  24. D. Ghosh, A. Deb, M. Mondal, and J. Ghosh, “Analysis of fluctuation of fluctuations in 32S-AgBr interactions at 200 AGeV,” Phys. Lett. B 540, 52–61 (2002).

    Article  ADS  Google Scholar 

  25. D. Ghosh, A. Deb, M. Mondal, and J. Ghosh, “Multiplicity- dependent chaotic pionization in ultra-relativistic nuclear interactions,” J. Phys. G: Nucl. Part. Phys. 29, 2087–2098 (2003).

    Article  ADS  Google Scholar 

  26. D. Ghosh, A. Deb, S. Bhattacharyya, and U. Datta, “Multiplicity scaling of target protons in high-energy nucleus-nucleus and hadron-nucleus interactions,” J. Phys. G: Nucl. Part. Phys. 39, 035101 (2012).

    Article  ADS  Google Scholar 

  27. M. S. Taqqu, V. Teverovsky, and W. Willinger, “Estimators for long-range dependence: an empirical study,” Fractals 03, 785–798 (1995).

    Article  MATH  Google Scholar 

  28. Z. Chen, P. C. Ivanov, K. Hu, and H. E. Stanley, “Effect of nonstationarities on detrended fluctuation analysis,” Phys. Rev. E 65, 041107 (2002).

    Article  ADS  Google Scholar 

  29. C. K. Peng, S. V. Buldyrev, S. Havlin, M. Simons, H. E. Stanley, and A. L. Goldberger, “Mosaic organization of DNA nucleotides,” Phys. Rev. E 49, 1685–1689 (1994).

    Article  ADS  Google Scholar 

  30. J. W. Kantelhardt, S. A. Zschiegner, E. Koscielny-Bunde, S. Havlin, A. Bunde, and H. Stanley, “Multifractal detrended fluctuation analysis of nonstationary time series,” Physica A 316, 87–114 (2002).

    Article  ADS  MATH  Google Scholar 

  31. J. W. Kantelhardt, E. Koscielny-Bunde, H. H. Rego, S. Havlin, and A. Bunde, “Detecting long-range correlations with detrended fluctuation analysis,” Physica A 295, 441–454 (2001).

    Article  ADS  MATH  Google Scholar 

  32. S. Bhaduri and D. Ghosh, “Speech, music and multifractality,” Curr. Sci. 110, 1817 (2016).

    Article  Google Scholar 

  33. S. Bhaduri and D. Ghosh, “Non-invasive detection of alzheimer’s disease—multifractality of emotional speech,” J. Neurol. Neurosci. (2016).

  34. S. Dutta, “Multifractal properties of ECG patterns of patients suffering from congestive heart failure,” J. Stat. Mech.: Theory Exp. 2010, 12021 (2010).

    Article  Google Scholar 

  35. S. Dutta, D. Ghosh, and S. Chatterjee, “Multifractal detrended fluctuation analysis of human gait diseases,” Front. Physiol. 4 (2013).

  36. D. Ghosh, S. Dutta, and S. Chakraborty, “Multifractal detrended cross-correlation analysis for epileptic patient in seizure and seizure free status,” Chaos, Solitons Fractals 67, 1–10 (2014).

    Article  ADS  MathSciNet  Google Scholar 

  37. Y. X. Zhang, W. Y. Qian, and C. B. Yang, “Multifractal structure of pseudorapidity and azimuthal distributions of the shower particles in Au + Au collisions at 200 A GeV,” Int. J. Mod. Phys. A 23, 2809–2816 (2008).

    Article  ADS  Google Scholar 

  38. D. Ghosh, A. Deb, and M. Lahiri, “Factorial and fractal analysis of the multipion production process at 350 GeV/c,” Phys. Rev. D 51, 3298–3304 (1995).

    Article  ADS  Google Scholar 

  39. D. Ghosh, A. Deb, P. Bandyopadhyay, M. Mondal, S. Bhattacharyya, J. Ghosh, and K. Kumar Patra, “Evidence of multifractality and constant specific heat in hadronic collisions at high energies,” Phys. Rev. C 65, 067902 (2002).

    Article  ADS  Google Scholar 

  40. D. Ghosh, A. Deb, S. Pal, P. K. Haldar, S. Bhattacharyya, P. Mandal, S. Biswas, and M. Mondal, “Evidence of fractal behavior of pions and protons in high energy interactions–an experimental investigation,” Fractals 13, 325–339 (2005).

    Article  Google Scholar 

  41. S. Dutta, D. Ghosh, and S. Chatterjee, “Multifractal detrended fluctuation analysis of pseudorapidity and azimuthal distribution of pions emitted in high energy nuclear collisions,” Int. J. Mod. Phys. A 29, 1450084 (2014).

    Article  ADS  Google Scholar 

  42. P. Mali, S. Sarkar, S. Ghosh, A. Mukhopadhyay, and G. Singh, “Multifractal detrended fluctuation analysis of particle density fluctuations in high-energy nuclear collisions,” Physica A 424, 25–33 (2015).

    Article  Google Scholar 

  43. L. Lacasa, B. Luque, F. Ballesteros, and J. Luque, “From time series to complex networks: the visibility graph,” Proc. Natl. Acad. Sci. USA 105, 4972–4975 (2008).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  44. L. Lacasa, B. Luque, and J. Luque, “The visibility graph: a new method for estimating the hurst exponent of fractional Brownian motion,” Europhys. Lett. 86, 30001 (2009).

    Article  ADS  Google Scholar 

  45. S. Jiang, C. Bian, X. Ning, and Q. D. Y. Ma, “Visibility graph analysis on heartbeat dynamics of meditation training,” Appl. Phys. Lett. 102, 253702 (2013).

    Article  ADS  Google Scholar 

  46. S. Bhaduri and D. Ghosh, “Electroencephalographic data analysis with visibility graph technique for quantitative assessment of brain dysfunction,” Clin. EEG Neurosci. 46, 218–223 (2015).

    Article  Google Scholar 

  47. A. Bhaduri and D. Ghosh, “Quantitative assessment of heart rate dynamics during meditation: an ECG based study with multi-fractality and visibility graph,” Front. Physiol. 7 (2016).

  48. G. Zebende, M. Silva, A. Rosa, A. Alves, J. de Jesus, and M. Moret, “Studying long-range correlations in a liquid-vapor-phase transition,” Physica A 342, 322–328 (2004).

    Article  ADS  Google Scholar 

  49. L. Zhao, W. Li, C. Yang, J. Han, Z. Su, Y. Zou, and X. Cai, “Multifractal and network analysis of phase transition,” (2017). doi 10.1371/journal.pone.0170467

    Google Scholar 

  50. S. Bhaduri and D. Ghosh, “Study of void probability scaling of pions in ultrarelativistic nuclear collision in fractal scenario,” (2017, in press).

    Google Scholar 

  51. N. S. Amelin, E. F. Staubo, L. P. Csernai, V. D. Toneev, K. K. Gudima, and D. Strottman, “Transverse flow and collectivity in ultrarelativistic heavy-ion collisions,” Phys. Rev. Lett. 67, 1523–1526 (1991).

    Article  ADS  Google Scholar 

  52. J.-Y. Ollitrault, “Anisotropy as a signature of transverse collective flow,” Phys. Rev. D 46, 229–245 (1992).

    Article  ADS  Google Scholar 

  53. S. Mrówczyński, “Plasma instability at the initial stage of ultrarelativistic heavy-ion collisions,” Phys. Lett. B 314, 118–121 (1993).

    Article  ADS  Google Scholar 

  54. M. Ahmadlou, H. Adeli, and A. Adeli, “Improved visibility graph fractality with application for the diagnosis of autism spectrum disorder,” Physica A 391, 4720–4726 (2012).

    Article  ADS  Google Scholar 

  55. C. F. Powell, P. H. Fowler, and D. H. Perkins, The Study of Elementary Particles by the Photographic Method (Pergamon, New York, 1959).

    Google Scholar 

  56. N. Agababyan, M. Atayan, and M. Charlet, J. Czyejewski, E. de Wolf, K. Dziunikowska, A. Endler, Z. Garutchava, H. Gulkanyan, R. Hakobyan, J. Karamyan, D. Kisielewska, W. Kittel, L. Liu, S. Mehrabyan, et al., “Self-affine fractality in π + p and K + p collisions at 250 GeV/c,” Phys. Lett. B 382, 305–311 (1996).

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Deepa Ghosh Research Foundation, Kolkata, 700031, India

    Anirban Bhaduri, Susmita Bhaduri & Dipak Ghosh

Authors
  1. Anirban Bhaduri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Susmita Bhaduri
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dipak Ghosh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anirban Bhaduri.

Additional information

The article is published in the original.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bhaduri, A., Bhaduri, S. & Ghosh, D. Azimuthal pion fluctuation in ultra relativistic nuclear collisions and centrality dependence—a study with chaos based complex network analysis. Phys. Part. Nuclei Lett. 14, 576–583 (2017). https://doi.org/10.1134/S1547477117040033

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1547477117040033

Search

Navigation