Abstract
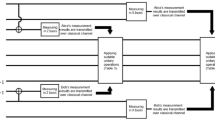
A variant of teleportation algorithm is suggested. It is based on using of multi-qubit states. Particularly, it allows the teleportation manager to create a proper entangled state between A and B and, consequently, to control the result of the teleportation between A and B. The problem of quantum secret sharing is considered in the framework of the suggested approach.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L. K. Grover, “Quantum Computers Can Search Arbitrarily Large Databases by a Single Query,” Phys. Rev. Lett. 79, 4709–4712 (1997).
C. H. Bennett, G. Brassard, C. Crepeau, R. Josza, A. Peres, and W. K. Wotters, “Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels,” Phys. Rev. Lett. 70, 1895–1899 (1993).
M. B. Plenio and V. Vedral, “Teleportation, Entanglement and Thermodynamics in the Quantum World,” Contemp. Phys. 39, 431–446 (1998).
D. Gottesman and I. L. Chuang, “Demonstrating the Viability of Universal Quantum Computation Using Teleportation and Single-Qubit Operations,” Nature 402, 390–392 (1999).
M. Hillery, V. Buzek, and A. Berthiaume, “Quantum Secret Sharing,” Phys. Rev. A 59, 1829–1834 (1999).
S. Lee, J. Joo, and J. Kim, “Entanglement of Three-Qubit Pure States in Terms of Teleportation Capability,” Phys. Rev. A: 72, 024302 (2005).
S. Lee, J. Joo, and J. Kim, “Teleportation Capability, Distillability, and Nonlocality on Three-Qubit States,” Phys. Rev. A 76, 012311-1–4 (2007).
D. Gottesman, “Theory of Quantum Secret Sharing,” Phys. Rev. A 61, 042311-1–8 (2000).
Author information
Authors and Affiliations
Corresponding author
Additional information
The article is published in the original.
Rights and permissions
About this article
Cite this article
Blinova, I.V., Popov, I.Y. Multi-qubit teleportation algorithm and teleportation manager. Phys. Part. Nuclei Lett. 8, 455–457 (2011). https://doi.org/10.1134/S1547477111050037
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1547477111050037