Friction Force and Radiative Heat Exchange in a System of Two Parallel Plates in Relative Motion: Corollaries of the Levine–Polevoi–Rytov Theory

Abstract

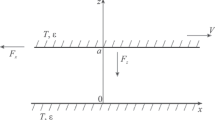
It has been shown that the fundamental results obtained in the works by Levine–Polevoi–Rytov (1980) and Rytov (1990) adequately describe the rate of radiative heat exchange and frictional force in a system of two thick parallel plates in relative motion, in full agreement with the results obtained by other authors later. A numerically calculated friction force for Drude metals turns out to be higher by a factor of 10⁷ than the early result obtained by Polevoi. In addition, the friction force significantly increases with increasing the conductivity of the plates or increasing the relaxation time of electrons with decreasing temperature.

APPENDIX

When calculating integrals in (30), (34), (38), and (40) with Drude function (44), it is expedient to write ${{\varepsilon }_{D}}(\omega )$ in the form

$${{\varepsilon }_{D}}(\omega ) = \left| \varepsilon \right|\exp (i\tilde {\phi }),$$

((A1))

$$\left| \varepsilon \right| = {{\left[ {{{{\left( {\frac{{1 + \kappa _{w}^{2}{{x}^{2}} - \kappa _{p}^{2}}}{{1 + \kappa _{w}^{2}{{x}^{2}}}}} \right)}}^{2}} + \frac{{{{{\tilde {\lambda }}}^{2}}}}{{{{x}^{2}}{{{(1 + \kappa _{w}^{2}{{x}^{2}})}}^{2}}}}} \right]}^{{1/2}}},$$

((A2))

$$\tilde {\phi } = \arctan \left( {\frac{{\kappa _{p}^{2}}}{{{{\kappa }_{w}}x(1 + \kappa _{w}^{2}{{x}^{2}} - \kappa _{p}^{2})}}} \right),$$

((A3))

where $\tilde {\lambda }$ = $\kappa _{p}^{2}{\text{/}}{{\kappa }_{w}}$. Accordingly, formulas (31), (33), (35), (37)–(41) for quantities U_1, 2, and ϕ_1, 2 reduce to

$${{U}_{1}} = {{\left[ {{{{\left( {{{y}^{2}} + \frac{{\lambda _{a}^{2}\kappa _{p}^{2}{{x}^{2}}}}{{1 + k_{w}^{2}{{x}^{2}}}}} \right)}}^{2}} + \frac{{{{\lambda }^{2}}{{x}^{2}}}}{{{{{(1 + \kappa _{w}^{2}{{x}^{2}})}}^{2}}}}} \right]}^{{1/4}}},$$

((31a))

$${{\phi }_{1}} = - 0.5\arctan \left[ {\frac{{\lambda x}}{{{{y}^{2}}(1 + \kappa _{w}^{2}{{x}^{2}}) + \lambda _{a}^{2}\kappa _{p}^{2}{{x}^{2}}}}} \right],$$

((33a))

$${{U}_{2}} = {{\left[ {{{{\left( { - {{y}^{2}} + \frac{{\kappa _{p}^{2}{{x}^{2}}}}{{1 + \kappa _{w}^{2}{{x}^{2}}}}} \right)}}^{2}} + \frac{{{{{\tilde {\lambda }}}^{2}}{{x}^{2}}}}{{{{{(1 + \kappa _{w}^{2}{{x}^{2}})}}^{2}}}}} \right]}^{{1/4}}},$$

((35a))

$${{\phi }_{2}} = - 0.5\arctan \left[ {\frac{{\tilde {\lambda }x}}{{\kappa _{p}^{2}{{x}^{2}} - {{y}^{2}}(1 + \kappa _{w}^{2}{{x}^{2}})}}} \right],$$

((37a))

$${{I}_{{\varepsilon 1}}} = \int\limits_0^\infty {dy{{y}^{3}}({{y}^{2}} + \lambda _{a}^{2}{{x}^{2}})U_{1}^{2}{{{\left| \varepsilon \right|}}^{{ - 2}}}{{{\left| {{{Q}_{{\varepsilon 1}}}} \right|}}^{{ - 2}}}{{{\sin }}^{2}}({{\phi }_{1}} - \tilde {\phi }),} $$

((38a))

$$\begin{gathered} {{\left| {{{Q}_{{\varepsilon 1}}}} \right|}^{2}} = {\text{|(}}{{y}^{2}} + U_{1}^{2}{{\left| \varepsilon \right|}^{{ - 2}}}\exp (2i({{\phi }_{1}} - \tilde {\phi })))\sinh (y) \\ + \;2y{{U}_{1}}{{\left| \varepsilon \right|}^{{ - 1}}}\exp (i({{\phi }_{1}} - \tilde {\phi })\cosh (y{\text{))}}{{{\text{|}}}^{2}}, \\ \end{gathered} $$

((39a))

$${{I}_{{\varepsilon 2}}} = \int\limits_0^x {dy{{y}^{3}}({{x}^{2}} - {{y}^{2}}){{U}_{2}}{{{\left| {{{Q}_{{\varepsilon 2}}}} \right|}}^{{ - 2}}}{{{\left| \varepsilon \right|}}^{{ - 2}}}{{{\sin }}^{2}}({{\phi }_{2}} - \tilde {\phi }),} $$

((40a))

$$\begin{gathered} {{\left| {{{Q}_{{\varepsilon 2}}}} \right|}^{2}} = {\text{|(}}{{y}^{2}} + U_{1}^{2}{{\left| \varepsilon \right|}^{{ - 2}}}\exp (2i({{\phi }_{1}} - \tilde {\phi })))\sin ({{\lambda }_{a}}y) \\ - \;2y{{U}_{1}}{{\left| \varepsilon \right|}^{{ - 1}}}\exp (i({{\phi }_{2}} - \tilde {\phi })\cos ({{\lambda }_{a}}y{\text{))}}{{{\text{|}}}^{2}}, \\ \end{gathered} $$

((41a))

where λ = $\kappa _{p}^{2}\lambda _{a}^{2}{\text{/}}{{\kappa }_{w}}$. Expressions (32), (34), (36), and (42) should be used taking into account modifications made for U_1, 2 and ϕ_1, 2.