Skip to main content
SpringerLink
Log in

Structural, Mechanical and Thermodynamic Properties of Cu2CoXS4 (X = Si, Ge, Sn) Studied by Density Functional Theory

  • Published:
Semiconductors Aims and scope Submit manuscript

Abstract

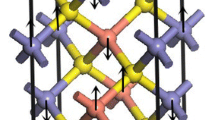
We have investigated the Structural, mechanical and thermodynamic properties of Cu2CoXS4 (X = Si, Ge, Sn) by using the density functional theory method. In this paper, we used GGA-PBE functional to find the equilibrium structural parameters and to calculate the elastic properties. The Mulliken population analysis indicates the bonds between S atoms and other three atoms in Cu2CoXS4 (X = Si, Ge, Sn) exhibit the feature of covalent bond. Furthermore, the calculated elastic constants prove the mechanical stability of Cu2CoXS4 (X = Si, Ge, Sn) in I\(\bar 4\) 2m structure. The results are given for B/G and AU reveal Cu2CoXS4 (X = Si, Ge, Sn) can behave as a ductile and elastic material. Finally, the heat capacity, thermal expansion, entropy and Debye temperature are also reported at the different pressures (0~50 GPa) and temperatures (0~1000 K).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Matsushita, T. Maeda, and A. Katsui, J. Cryst. Growth 208, 416 (2000).

    Article  ADS  Google Scholar 

  2. W. Schafer and R. Nitsche, Mater. Res. Bull. 9, 645 (1974).

    Article  Google Scholar 

  3. L. Guen and W. S. Glaunsinger, J. Solid State Chem. 35, 10 (1980).

    Article  ADS  Google Scholar 

  4. A. Gupta, K. Mokurala, A. Kamble, S. Shankar, and S. Mallick, Solid State Phys. 1665, 140022 (2015).

    Google Scholar 

  5. T. Bernert and A. Pfitzner, Zeitschr. Anorg. Allgem. Chem. 632, 1213 (2010).

    Article  Google Scholar 

  6. S. R. Hall, J. T. Szymanski, and J. M. Stewart, Can. Mineral. 2, 131 (1978).

    Google Scholar 

  7. K. Mokurala, A. Kamble, and P. Bhargava, in Proceedings of the IEEE Photovoltaic Specialist Conference, 2015, p. 1.

    Google Scholar 

  8. A. Ghosh, D. K. Chaudhary, and A. Biswas, RSC Adv. 6, 115204 (2016).

    Article  Google Scholar 

  9. X. Y. Zhang, N. Z. Bao, and K. Ramasamy, Chem. Commun. 43, 4956 (2012).

    Article  Google Scholar 

  10. F. D. Benedetto, G. P. Bernardini, and D. Borrini, Phys. Chem. Miner. 31, 683 (2005).

    Article  Google Scholar 

  11. Y. Cui, R. P. Deng, and G. Wang, J. Mater. Chem. 22, 23136 (2012).

    Article  Google Scholar 

  12. X. Y. Zhang, N. Z. Bao, B. P. Lin, and A. Gupta, Nanotechnology 24, 105706 (2013).

    Article  ADS  Google Scholar 

  13. M. A. Macias, M. Quintero, and E. Moreno, Rev. Latinoam. Metalurg. Mater. 34, 28 (2014).

    Google Scholar 

  14. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson, and M. C. Payne, Zeitschr. Kristallogr. 220, 567 (2005).

    ADS  Google Scholar 

  15. J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).

    Article  ADS  Google Scholar 

  16. L. Guo, G. Hu, and W. J. Feng, Struct. Acta Phys.- Chim. Sin. 29, 929 (2013).

    Google Scholar 

  17. J. H. Yuan, B. Gao, W. Wang, et al., Acta Phys.-Chim. Sin. 31, 1302 (2015).

    Google Scholar 

  18. Y. J. Dong and Y. L. Gao, Chalcogenide Lett. 13, 515 (2016).

    Google Scholar 

  19. Z. J. Liu, X. W. Sun, and X. M. Tan, Solid State Commun. 144, 264 (2007).

    Article  ADS  Google Scholar 

  20. M. A. Blanco, A. M. Pendas, and E. Francisco, J. Mol. Struct.: THEOCHEM 368, 245 (1996).

    Article  Google Scholar 

  21. E. Francisco, J. M. Recio, and M. A. Blanco, J. Phys. Chem. A 102, 1595 (2013).

    Article  Google Scholar 

  22. F. Birch, J. Geophys. Res. 83, 1257 (1978).

    Article  ADS  Google Scholar 

  23. F. Birch, Phys. Rev. 71, 809 (1947).

    Article  ADS  Google Scholar 

  24. F D. Murnaghan, Proc. Natl. Acad. Sci. U.S.A. 30, 244 (1944).

    Article  ADS  Google Scholar 

  25. Y. J. Dong and Y. L. Gao, Yunnan Normal Univ. 36, 14 (2016).

    Google Scholar 

  26. M. Born and K. Huang, Dynamical Theory of Crystal Lattices (Clarendon, Oxford, 1988)

    MATH  Google Scholar 

  27. S. O. Kart and T. Cagin, J. Alloys Compd. 508, 177 (2010)

    Article  Google Scholar 

  28. R. Hill, Proc. Phys. 65, 349 (1952).

    Article  ADS  Google Scholar 

  29. S. F. Pugh, Philos. Mag. 45, 823 (2009).

    Article  Google Scholar 

  30. X. Zhang, C. Ying, and Z. Li, Superlatt. Microstruct. 52, 459 (2012).

    Article  ADS  Google Scholar 

  31. I. N. Frantsevich, F. F. Voronov, and S. A. Bokuta, in Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, Ed. by I. N. Frantsevich (Naukova Dumka, Kiev, 1983), p. 60 [in Russian].

  32. S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett. 101, 055504 (2008)

    Article  ADS  Google Scholar 

  33. H. Chen, L. Yang, and J. Long, Superlatt. Microstruct. 79, 156 (2014).

    Article  Google Scholar 

  34. M. A. Blanco, E. Francisco, and V. Luaña, Comput. Phys. Commun. 158, 57 (2004).

    Article  ADS  Google Scholar 

  35. E. Francisco, M. A. Blanco, and G. Sanjurjo, Phys. Rev. B 63, 385 (2001).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Science and Technology, Xinyang University, Xinyang, 464000, China

    Yu Jing Dong & Yan Li Gao

  2. Institute of Atomic and Molecular Physics, Sichuan University, Chengdu, 610065, China

    Yu Jing Dong

Authors
  1. Yu Jing Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yan Li Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu Jing Dong.

Additional information

The article is published in the original.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dong, Y.J., Gao, Y.L. Structural, Mechanical and Thermodynamic Properties of Cu2CoXS4 (X = Si, Ge, Sn) Studied by Density Functional Theory. Semiconductors 52, 414–419 (2018). https://doi.org/10.1134/S1063782618040127

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1063782618040127

Search

Navigation