Skip to main content
SpringerLink
Log in

Well-posedness analysis and numerical implementation of a linearized two-dimensional bottom sediment transport problem

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

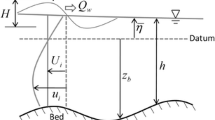
A two-dimensional linearized model of coastal sediment transport due to the action of waves is studied. Up till now, one-dimensional sediment transport models have been used. The model under study makes allowance for complicated bottom relief, the porosity of the bottom sediment, the size and density of sediment particles, gravity, wave-generated shear stress, and other factors. For the corresponding initial–boundary value problem the uniqueness of a solution is proved, and an a priori estimate for the solution norm is obtained depending on integral estimates of the right-hand side, boundary conditions, and the norm of the initial condition. A conservative difference scheme with weights is constructed that approximates the continuous initial–boundary value problem. Sufficient conditions for the stability of the scheme, which impose constraints on its time step, are given. Numerical experiments for test problems of bottom sediment transport and bottom relief transformation are performed. The numerical results agree with actual physical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. O. Leont’ev, Coastal Dynamics: Waves, Currents, and Sediment Flow (GEOS, Moscow, 2001) [in Russian].

    Google Scholar 

  2. Liu Xiaoying, Qi Shi, Huang Yuan, Chen Yuehong, and Du Pengfei, “Predictive modeling in sediment transportation across multiple spatial scales in the Jialing River basin of China,” Int. J. Sediment Res. 30 (3), 250–255 (2015).

    Article  Google Scholar 

  3. G. I. Marchuk, V. P. Dymnikov, and V. B. Zalesny, Mathematical Models in Geophysical Hydrodynamics and Numerical Methods of Their Implementation (Gidrometeoizdat, Leningrad, 1987) [in Russian].

    Google Scholar 

  4. A. I. Sukhinov, A. E. Chistyakov, E. F. Timofeeva, and A. V. Shishenya, “Mathematical model for calculating coastal wave processes,” Math. Models Comput. Simul. 5 (2), 122–129 (2013).

    Article  MathSciNet  Google Scholar 

  5. A. I. Sukhinov, A. E. Chistyakov, and E. A. Protsenko, “Mathematical modeling of sediment transport in the coastal zone of shallow reservoirs,” Math. Models Comput. Simul. 6 (4), 351–363 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  6. A. I. Sukhinov, A. E. Chistyakov, and E. A. Protsenko, “Mathematical modeling of sediment transport in coastal systems on multiprocessor computers,” Vychisl. Metody Program. Novye Vychisl. Tekhnol. 15 (4), 610–620 (2014).

    Google Scholar 

  7. A. I. Sukhinov, E. A. Protsenko, A. E. Chistyakov, and S. A. Shreter, “Comparison of numerical efficiency of explicit and implicit schemes as applied to sediment transport in coastal systems,” Vychisl. Metody Program. Novye Vychisl. Tekhnol. 16 (3), 328–338 (2015).

    Google Scholar 

  8. A. V. Shishenya and A. I. Sukhinov, “Development of a regularized mathematical model for modeling hydrodynamics and surge phenomena in shallow water basins and its parallel implementation on a parallel shared memory computer system,” Izv. Yuzhn. Fed. Univ. Tekh. Nauki 161 (12), 219–230 (2014).

    Google Scholar 

  9. B. N. Chetverushkin, “Resolution limits of continuous media models and their mathematical formulations,” Math. Models Comput. Simul. 5 (3), 266–279 (2013).

    Article  MathSciNet  Google Scholar 

  10. V. S. Vladimirov, Equations of Mathematical Physics (Marcel Dekker, New York, 1971; Nauka, Moscow, 1981).

    MATH  Google Scholar 

  11. O. A. Ladyzhenskaya, The Boundary Value Problems of Mathematical Physics (Nauka, Moscow, 1973; Springer- Verlag, New York, 1985).

    Google Scholar 

  12. O. A. Ladyzhenskaya, V. A. Solonnikov, and N. N. Ural’tseva, Linear and Quasilinear Equations of Parabolic Type (Nauka, Moscow, 1967; Am. Math. Soc., Providence, R.I., 1968).

    MATH  Google Scholar 

  13. A. A. Samarskii, The Theory of Difference Schemes (Nauka, Moscow, 1983; Marcel Dekker, New York, 2001).

    MATH  Google Scholar 

  14. V. S. Vasil’ev and A. I. Sukhinov, “Precise two-dimensional models for shallow water basins,” Mat. Model. 15 (10), 17–34 (2003).

    MathSciNet  Google Scholar 

  15. A. I. Sukhinov, “Precise fluid dynamics models and their application in prediction and reconstruction of extreme events in the Sea of Azov,” Izv. Taganrog. Radiotech. Univ., No. 3, 228–235 (2006).

    Google Scholar 

  16. A. I. Sukhinov and A. V. Shishenya, “Increasing efficiency of alternating triangular method based on improved spectral estimates,” Math. Models Comput. Simul. 5 (3), 257–265 (2013).

    Article  MathSciNet  Google Scholar 

  17. A. I. Sukhinov and A. E. Chistyakov, “Adaptive modified alternating triangular iterative method for solving grid equations with a non-self-adjoint operator,” Math. Models Comput. Simul. 4 (4), 398–409 (2012).

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Chekhov Taganrog Institute, Branch of Rostov State University of Economics, Taganrog, 347936, Russia

    V. V. Sidoryakina

  2. Don State Technical University, Rostov-on-Don, 344000, Russia

    A. I. Sukhinov

Authors
  1. V. V. Sidoryakina
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. I. Sukhinov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. V. Sidoryakina.

Additional information

Original Russian Text © V.V. Sidoryakina, A.I. Sukhinov, 2017, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2017, Vol. 57, No. 6, pp. 985–1002.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sidoryakina, V.V., Sukhinov, A.I. Well-posedness analysis and numerical implementation of a linearized two-dimensional bottom sediment transport problem. Comput. Math. and Math. Phys. 57, 978–994 (2017). https://doi.org/10.1134/S0965542517060124

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542517060124

Keywords

Search

Navigation