Abstract
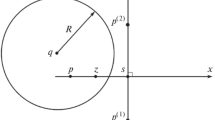
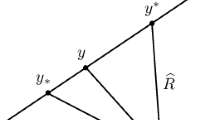
We study α-sets in Euclidean space ℝn. The notion of α-set is introduced as a generalization of a convex closed set in ℝn. This notion appeared in the study of reachable sets and integral funnels of nonlinear control systems in Euclidean spaces. Reachable sets of nonlinear dynamic systems are usually nonconvex, and the degree of their nonconvexity is different in different systems. This circumstance prompted the introduction of a classification of sets in ℝn according to the degree of their nonconvexity. Such a classification stems from control theory and is presented here in terms of α-sets in ℝn.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. N. Ushakov, A. A. Uspenskii, and A. N. Fomin, α-Sets and Their Properties (Inst. Mat. Mekh. UrO RAN, Yekaterinburg, 2004) [in Russian].
B. N. Pshenichnyi, Convex Analysis and Extremal Problems (Nauka, Moscow, 1980) [in Russian].
E. S. Polovinkin and M. V. Balashov, Elements of Convex and Strongly Convex Analysis (Fizmatlit, Moscow, 2007) [in Russian].
V. N. Ushakov, A. A. Uspenskii, and P. D. Lebedev, “Construction of a minimax solution for an eikonal-type equation,” Proc. Steklov Inst. Math., Suppl. 2, S191–S201 (2008).
V. N. Ushakov, A. A. Uspenskii, and T. B. Tokmantsev, “Stable bridges in differential games in a finite time interval,” Proc. Steklov Inst. Math., Suppl. 2, S168–S192 (2005).
A. A. Uspenskii and P. D. Lebedev, “Construction of the optimal outcome function for a time-optimal problem on the basis of a symmetry set,” Autom. Remote Control 70 (7), 1132–1139 (2009).
A. A. Uspenskii and P. D. Lebedev, “Geometry and asymptotics of wavefronts,” Russian Math. (Iz. VUZ) 52 (3), 24–33 (2008).
A. A. Uspenskii and P. D. Lebedev, “On the set of limit values of local diffeomorphisms in wavefront evolution,” Proc. Steklov Inst. Math. 272 (Suppl. 1), S255–S270 (2011).
T. Motzkin, “Sur quelques propriétés caractéristiques des ensembles convexes,” Atti Accad. Naz. Lincei 21, 562–567 (1935).
G. Bouligand, “Sur les surfaces depourvues de points hyperlimites,” Ann. Soc. Polon. Math. 9, 32–41 (1930).
V. F. Dem’yanov and A. M. Rubinov, Foundations of Nonsmooth Analysis and Quasi-Differential Calculus (Nauka, Moscow, 1990) [in Russian].
B. M. Makarov and A. N. Podkorytov, Lectures on Real Analysis (BKhV-Peterburg, St. Petersburg, 2011) [in Russian].
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © V.N. Ushakov, A.A. Uspenskii, 2016, published in Trudy Instituta Matematiki i Mekhaniki UrO RAN, 2016, Vol. 22, No. 2.
Rights and permissions
About this article
Cite this article
Ushakov, V.N., Uspenskii, A.A. Theorems on the Separability of α-Sets in Euclidean Space. Proc. Steklov Inst. Math. 299 (Suppl 1), 231–245 (2017). https://doi.org/10.1134/S0081543817090255
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0081543817090255