Skip to main content
SpringerLink
Log in

Critical behavior of a monoaxial chiral helimagnet

  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

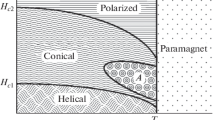
We analyze the critical behavior of magnetically ordered phases appearing in a monoaxial chiral helimagnet in a weak external magnetic field. Using the formalism of the equations of state in the critical region, we determine the temperature dependence of the order parameters for the conical phase and the soliton-lattice phase. We calculated the critical exponents and show that they coincide with those in the three-dimensional Heisenberg model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Y. Ishikawa, K. Tajima, D. Bloch, and M. Roth, “Helical spin structure in manganese silicide MnSi,” Solid State Commun., 19, 525–528 (1976).

    Article  ADS  Google Scholar 

  2. S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neuebauer, R. Georgii, and P. Böni, “Skyrmion lattice in a chiral magnet,” Science, 323, 915–919 (2009).

    Article  ADS  Google Scholar 

  3. X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa, and Y. Tokura, “Real-space observation of a two-dimensional skyrmion crystal,” Nature, 465, 901–904 (2010).

    Article  ADS  Google Scholar 

  4. W. Münzer, A. Neubauer, T. Adams, S. Mühlbauer, C. Franz, F. Jonietz, R. Georgii, P. Böni, B. Pedersen, M. Schmidt, A. Rosch, and C. Pfleiderer, “Skyrmion lattice in the doped semiconductor Fe1−x CoxSi,” Phys. Rev. B, 81, 041203 (2010).

    Article  ADS  Google Scholar 

  5. B. Lebech, J. Bernhard, and T. Freltoft, “Magnetic structures of cubic FeGe studied by small-angle neutron scattering,” J. Phys.: Condens. Matter, 1, 6105–6122 (1989).

    ADS  Google Scholar 

  6. X. Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W. Z. Zhang, S. Ishiwata, Y. Matsui, and Y. Tokura, “Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe,” Nature Mater., 10, 106–109 (2011).

    Article  ADS  Google Scholar 

  7. K. Kohn, “A new ferrimagnet Cu2SeO4,” J. Phys. Soc. Japan, 42, 2065–2066 (1977).

    Article  ADS  Google Scholar 

  8. S. Seki, X. Z. Yu, S. Ishiwata, and Y. Tokura, “Observation of skyrmions in a multiferroic material,” Science, 336, 198–201 (2012).

    Article  ADS  Google Scholar 

  9. T. Moriya and T. Miyadai, “Evidence for the helical spin structure due to antisymmetric exchange interaction in Cr13NbS2,” Solid State Commun., 42, 209–212 (1982).

    Article  ADS  Google Scholar 

  10. T. Miyadai, K. Kikuchi, H. Kondo, S. Sakka, M. Arai, and Y. Ishikawa, “Magnetic properties of Cr13NbS2,” J. Phys. Soc. Japan, 52, 1394–1401 (1983).

    Article  ADS  Google Scholar 

  11. U. K. Rößler, A. N. Bogdanov, and C. Pfleiderer, “Spontaneous skyrmion ground states in magnetic metals,” Nature, 442, 797–801 (2006).

    Article  ADS  Google Scholar 

  12. N. Nagaosa and Y. Tokura, “Topological properties and dynamics of magnetic skyrmions,” Nature Nanotech., 8 (2013).

    Google Scholar 

  13. I. E. Dzyaloshinskii, “Theory of helicoidal structures in antiferromagnets: I. Nonmetals,” Sov. Phys. JETP, 19, 960–971 (1964); “The theory of helicoidal structures in antiferromagnets: II. Metals,” Sov. Phys. JETP, 20, 223–231 (1965).

    Google Scholar 

  14. Yu. A. Izyumov, “Modulated, or long-periodic, magnetic structures of crystals,” Sov. Phys. Usp., 27, 845–887 (1984).

    Article  ADS  Google Scholar 

  15. Y. Togawa, T. Koyama, K. Takayanagi, S. Mori, Y. Kousaka, J. Akimitsu, S. Nishihara, K. Inoue, A. S. Ovchinnikov, and J. Kishine, “Chiral magnetic soliton lattice on a chiral helimagnet,” Phys. Rev. Lett., 108, 107202 (2012).

    Article  ADS  Google Scholar 

  16. J. Kishine and A. S. Ovchinnikov, “Theory of monoaxial chiral helimagnet,” in: Solid State Physics (R. E. Camley and R. L. Stamps, eds.), Vol. 66, Acad. Press, New York (2015), pp. 1–130.

    Google Scholar 

  17. I. Dzyaloshinskii, “A thermodynamic theory of ‘weak’ ferromagnetism of antiferromagnetics,” J. Phys. Chem. Solids, 4, 241–255 (1958).

    Article  ADS  Google Scholar 

  18. T. Moriya, “Anisotropic superexchange interaction and weak ferromagnetism,” Phys. Rev., 120, 91–98 (1960).

    Article  ADS  Google Scholar 

  19. Y. Kousaka, Y. Nakao, J. Kishine, M. Akita, K. Inoue, and J. Akimitsu, “Chiral helimagnetism in T1/3NbS2 (T = Cr and Mn),” Nucl. Instrum. Methods Phys. Res. A, 600, 250–253 (2009).

    Article  ADS  Google Scholar 

  20. N. J. Ghimire, M. A. McGuire, D. S. Parker, B. Sipos, S. Tang, J.-Q. Yan, B. C. Sales, and D. Mandrus, “Magnetic phase transition in single crystals of the chiral helimagnet Cr1/3NbS2,” Phys. Rev. B, 87, 104403 (2013).

    Article  ADS  Google Scholar 

  21. S. V. Grigoriev, S. V. Maleyev, A. I. Okorokov, Yu. O. Chetverikov, and H. Eckerlebe, “Field-induced reorientation of the spin helix in MnSi near T c,” Phys. Rev. B, 73, 224440 (2006).

    Article  ADS  Google Scholar 

  22. S. V. Grigoriev, V. A. Dyadkin, D. Menzel, J. Schoenes, Yu. O. Chetverikov, A. I. Okorokov, H. Eckerlebe, and S. V. Maleyev, “Magnetic structure of Fe1−x CoxSi in a magnetic field studied via small-angle polarized neutron diffraction,” Phys. Rev. B, 76, 224424 (2007).

    Article  ADS  Google Scholar 

  23. C. Pappas, E. Lelièvre-Berna, P. Falus, P. M. Bentley, E. Moskvin, S. Grigoriev, P. Fouquet, and B. Farago, “Chiral paramagnetic skyrmion-like phase in MnSi,” Phys. Rev. Lett., 102, 197202 (2009).

    Article  ADS  Google Scholar 

  24. S. A. Brazovskii, “Phase transition of an isotropic system to a nonuniform state,” Sov. Phys. JETP, 41, 85–89 (1975).

    ADS  Google Scholar 

  25. F. B. Mushenok, “Homogeneous and Goldstone modes of spin excitations in Cr1/3NbS2 helimagnet,” Eur. Phys. J. B, 86, 342 (2013).

    Article  ADS  Google Scholar 

  26. V. Dyadkin, F. Mushenok, A. Bosak, D. Menzel, S. Grigoriev, P. Pattison, and D. Chernyshov, “Structural disorder versus chiral magnetism in Cr1/3NbS2,” Phys. Rev. B, 91, 184205 (2015).

    Article  ADS  Google Scholar 

  27. I. Živković, J. S. White, H. M. Rønnow, K. Prša, and H. Berger, “Critical scaling in the cubic helimagnet Cu2OSeO3,” Phys. Rev. B, 89, 060401 (2014).

    Google Scholar 

  28. Y. Nishikawa and K. Hukushima, “Phase transitions and ordering structures of a model of chiral helimagnet in three dimensions,” Phys. Rev. B, 94, 064428 (2016); arXiv:1603.04200v1 [cond-mat.stat-mech] (2016).

    Article  ADS  Google Scholar 

  29. L. Klein and A. Aharony, “Crossover and multicriticality due to the Dzyaloshinsky–Moriya interaction,” Phys. Rev. B, 44, 856–858 (1991).

    Article  ADS  Google Scholar 

  30. L. L. Liu, “Effect of antisymmetric interactions on critical phenomena: A system with helical ground state,” Phys. Rev. Lett., 31, 459–462 (1973).

    Article  ADS  Google Scholar 

  31. E. Brézin, D. J. Wallace, and K. G. Wilson, “Feynman-graph expansion for the equation of state near the critical point,” Phys. Rev. B, 7, 232–239 (1973).

    Article  ADS  Google Scholar 

  32. S.-K. Ma, Modern Theory of Critical Phenomena, Benjamin, Reading, Mass. (1976).

    Google Scholar 

  33. B. I. Halperin and P. C. Hohenberg, “Scaling laws for dynamic critical phenomena,” Phys. Rev., 177, 952–971 (1969).

    Article  ADS  Google Scholar 

  34. K. G. Wilson and J. Kogut, “The renormalization group and the ϵ expansion,” Phys. Rep. C, 12, 75–199 (1974).

    Article  ADS  Google Scholar 

  35. A. Aharony, “Equation of state for cubic ferromagnets,” Phys. Rev. B, 10, 3006–3009 (1974).

    Article  ADS  Google Scholar 

  36. M. Shinozaki, S. Hoshino, Y. Masaki, J. Kishine, and Y. Kato, “Finite-temperature properties of threedimensional chiral helimagnets,” J. Phys. Soc. Japan, 85, 074710 (2016); arXiv:1512.00235v3 [cond-mat.str-el] (2015).

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Natural Sciences, Yeltsin Ural Federal University, Ekaterinburg, Russia

    A. S. Ovchinnikov, I. G. Bostrem & Vl. E. Sinitsyn

  2. Division of Natural and Environmental Sciences, The Open University of Japan, Chiba, Japan

    J. Kishine

Authors
  1. A. S. Ovchinnikov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. G. Bostrem
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vl. E. Sinitsyn
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. J. Kishine
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. S. Ovchinnikov.

Additional information

This research was supported by the Japan Society for the Promotion of Science, KAKENHI Program (Grant Nos. 25287087 and 25220803), the Russian Government (Document 211, Contract No. 02.A03.21.0006), the Russian Ministry of Education and Science (Project Nos. 1437 and 2725), and the Russian Foundation for Basic Research (Grant No. 17-52-500131).

The research of Vl. E. Sinitsyn is supported by the Support Program for Young Scientists with a Candidate’s Degree (Grant No. MK-6230.2016.2).

Translated from Teoreticheskaya i Matematicheskaya Fizika, Vol. 191, No. 3, pp. 518–534, June, 2017.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ovchinnikov, A.S., Bostrem, I.G., Sinitsyn, V.E. et al. Critical behavior of a monoaxial chiral helimagnet. Theor Math Phys 191, 924–938 (2017). https://doi.org/10.1134/S0040577917060101

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040577917060101

Keywords

Search

Navigation