Abstract
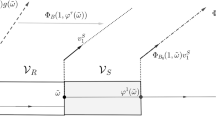
The generalization of the Mishchenko–Fomenko theorem for symplectic superintegrable systems to the case of an arbitrary, not necessarily compact, invariant submanifold allows giving a global description of a superintegrable Hamiltonian system, which can be split into several nonequivalent globally superintegrable systems on nonoverlapping open submanifolds of the symplectic phase manifold having both compact and noncompact invariant submanifolds. A typical example of such a composition of globally superintegrable systems is motion in a centrally symmetric field, in particular, the two-dimensional Kepler problem.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. S. Mishchenko and A. T. Fomenko, “Generalized Liouville method of integration of Hamiltonian systems,” Funct. Anal. Appl., 12, 113–121 (1978).
A. V. Bolsinov and B. Jovanović, “Noncommutative integrability, moment map, and geodesic flows,” Ann. Global Anal. Geom., 23, 305–322 (2003).
F. Fassò, “Francesco superintegrable Hamiltonian systems: Geometry and perturbations,” Acta Appl. Math., 87, 93–121 (2005).
V. I. Arnold, ed., Dynamical Systems III, IV, Springer, Berlin (1990).
V. F. Lazutkin, KAM Theory and Semiclassical Approximations to Eigenfunctions (Ergeb. Math. Grenzgeb., Vol. 24), Springer, Berlin (1993).
G. Giachetta, L. Mangiarotti, and G. Sardanashvily, “Bi-Hamiltonian partially integrable systems,” J. Math. Phys., 44, 1984–1997 (2003).
E. Fiorani, G. Giachetta, and G. Sardanashvily, “The Liouville–Arnold–Nekhoroshev theorem for non-compact invariant manifolds,” J. Phys. A, 36, L101–L107 (2003).
E. Fiorani and G. Sardanashvily, “Noncommutative integrability on noncompact invariant manifolds,” J. Phys. A, 39, 14035–14042 (2006).
G. Sardanashvily, “Superintegrable Hamiltonian systems with noncompact invariant submanifolds: Kepler system,” Internat. J. Geom. Methods Modern Phys., 6, 1391–1414 (2009).
G. Sardanashvily, Handbook of Integrable Hamiltonian Systems, URSS, Moscow (2015).
E. Fiorani and G. Sardanashvily, “Global action–angle coordinates for completely integrable systems with noncompact invariant submanifolds,” J. Math. Phys., 48, 032901 (2007).
J. Duistermaat, “On global action–angle coordinates,” Commun. Pure Appl. Math., 33, 687–706 (1980).
P. Dazord and T. Delzant, “Le probleme general des variables actions–angles,” J. Differ. Geom., 26, 223–251 (1987).
I. Vaisman, Lectures on the Geometry of Poisson Manifolds (Progr. Math., Vol. 118), Birkhäuser, Basel (1994).
R. S. Palais, A Global Formulation of the Lie Theory of Transformation Groups (Memoirs Amer. Math. Soc., Vol. 22), Amer. Math. Soc., Providence, R. I. (1957).
G. Meigniez, “Submersions, fibrations, and bundles,” Trans. Amer. Math. Soc., 354, 3771–3787 (2002).
V. Guillemin and S. Sternberg, Symplectic Techniques in Physics, Cambridge Univ. Press, Cambridge (1984).
H. J. Sussmann, “Orbits of families of vector fields and integrability of distributions,” Trans. Amer. Math. Soc., 180, 171–188 (1973).
R. H. Cushman and L. M. Bates, Global Aspects of Classical Integrable Systems, Birkhäuser, Basel (1997).
E. Fiorani, “Momentum maps, independent first integrals, and integrability for central potentials,” Internat. J. Geom. Methods Modern Phys., 6, 1323–1341 (2009).
A. Kurov and G. Sardanashvily, “Partially superintegrable systems on Poisson manifolds,” arXiv:1606.03868v1 [math-ph] (2016).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Teoreticheskaya i Matematicheskaya Fizika, Vol. 191, No. 3, pp. 389–406, June, 2017.
Rights and permissions
About this article
Cite this article
Kurov, A.V., Sardanashvily, G.A. Globally superintegrable Hamiltonian systems. Theor Math Phys 191, 811–826 (2017). https://doi.org/10.1134/S0040577917060022
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0040577917060022