Abstract
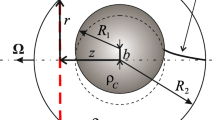
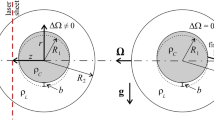
Steady flow generated by oscillations of an inner solid core in a fluid-filled rotating spherical cavity is experimentally studied. The core with density less than the fluid density is located near the center of the cavity and is acted upon by a centrifugal force. The gravity field directed perpendicular to the rotation axis leads to a stationary displacement of the core from the rotation axis. As a result, in the frame of reference attached to the cavity, the core performs circular oscillation with frequency equal to the rotation frequency, and its center moves along a circular trajectory in the equatorial plane around the center of the cavity. For the differential rotation of the core to be absent, one of the poles of the core is connected to the nearest pole of the cavity with a torsionally elastic, flexible fishing line. It is found that the oscillation of the core generates axisymmetric azimuthal fluid flow in the cavity which has the form of nested liquid columns rotating with different angular velocities. Comparison with the case of a free oscillating core which performs mean differential rotation suggests the existence of two mechanisms of flow generation (due to the differential rotation of the core in the Ekman layer and due to the oscillation of the core in the oscillating boundary layers).
Similar content being viewed by others
References
G. S. Golitsyn, Introduction to the Dynamics of Planetary Atmospheres (Gidrometeoizdat, Leningrad, 1973) [in Russian].
P. Cardin and P. Olson, Experiments on Core Dynamics (Elsevier, New York, 2007), 319–343. (Treatise on Geophysics, Vol. 8).
Yu. N. Belyaev and I. M. Yavorskaya, “Viscous Flow in a Rotating Spherical Layer and Their Stability,” Itogi Nauki Tekh., Ser. Mekh. Zhidk. Gaza 15 (1980).
B. R. Munson and M. Menguturk, “Viscous Incompressible Flow between Concentric Rotating Spheres. Pt 3. Linear Stability and Experiment,” J. Fluid Mech. 69 (4), 705–719 (1975).
D. Yu. Zhilenko and O. E. Krivonosova, “Quasi-Two-Dimensional and Three-Dimensional Turbulence in Rotating Spherical Layers of a Fluid,” Pis’ma Zh. Eksp. Teor. Fiz. 101 (8), 583–588 (2015).
M. Hoff, U. Harlander, and C. Egbers, “Experimental Survey of Linear and Non-Linear Inertial Waves and Wave Instabilities in a Spherical Shell,” Fluid Mech. 789, 589–616 (2016).
C. G. Kozlov and N. V. Kozlov, “Hydrodynamic Vibratory Gyroscope,” Dokl. Akad. Nauk 415 (6), 759–762 (2007).
C. G. Kozlov and N. V. Kozlov, and S. V. Subbotin, “Motion of a Fluid and a Solid Core in a Spherical Cavity Rotating in an External Force Field,” Dokl. Akad. Nauk 454 (2), 173–177 (2014).
V. G. Kozlov, N. V. Kozlov, and S. V. Subbotin, “The Effect of Oscillating Force Field on the Dynamics of Free Inner Core in a Rotating Fluid-Filled Spherical Cavity,” Phys. Fluids 27 (12), 124101 (2015).
M. Le Bars, D. Cébron, and P. Le Gal, “Flows Driven by Libration, Precession, and Tides,” Annual Rev. Fluid Mech. 47, 163–193 (2015).
C. Morize, M. Le Bars, P. Le Gal, and A. Tilgner, “Experimental Determination of Zonal Winds Driven by Tides,” Phys. Rev. Lett. 104, 214501 (2010).
F. H. Busse, “Mean Zonal Flows Generated by Librations of a Rotating Spherical Cavity,” J. Fluid Mech. 650, 505–512 (2010).
J. Noir, D. Jault, and P. Cardin, “Numerical Study of the Motions within a Slowly Precessing Sphere at Low Ekman Number,” J. Fluid Mech. 437, 283–299 (2001).
V. G. Kozlov, N. V. Kozlov, and S. V. Subbotin, “Steady Flows Excited by Circular Oscillations of Free Inner Core in Rotating Spherical Cavity,” Europ. J. Mech., B: Fluids 58 (4), 85–94 (2016).
W. Thielicke and E. J. Stamhuis, “PIVlab—Towards User-Friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB,” J. Open Res. Software 2 (1), e30 (2014).
Kh. P. Greenspan, The Theory of Rotating Fluids (Cambridge Univ. Press, London, 1968).
R. Kerswell, “On the Internal Shear Layers Spawned by the Critical Regions in Oscillatory Ekman Boundary Layers,” J. Fluid Mech. 298, 311–325 (1995).
V. G. Kozlov, N. V. Kozlov, and S. V. Subbotin, “Influence of an External Force Field on the Dynamics of a Free Core and Fluid in a Rotating Spherical Cavity,” Phys. Fluids 27 (7), 074106 (2015).
N. Schaeffer and P. Cardin, “Quasi-Geostrophic Model of the Instabilities of the Stewartson Layer in Flat and Depth Varying Containers,” Phys. Fluids 17, 104111 (2005).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © V.G. Kozlov, S.V. Subbotin.
Rights and permissions
About this article
Cite this article
Kozlov, V.G., Subbotin, S.V. Steady Flow Generated by a Core Oscillating in a Rotating Spherical Cavity. J Appl Mech Tech Phy 59, 22–31 (2018). https://doi.org/10.1134/S0021894418010042
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0021894418010042