Photovoltaic Effect in Phthalocyanine-Based Organic Solar Cells: 3. Exciton Trapping Followed by Charge Carrier Generation

Abstract

A kinetic model Nd(Na) of the photovoltaic effect in phthalocyanine (Pc) layers doped with a donor D (acceptor A) in concentration forming one impurity level with energy E_D (E_A) in the band gap is proposed. The photovoltaic effect is due to the transfer of energy of molecular excitons S₁ to neutral A(D) and ionized A⁻(D⁺) impurities followed by the formation of electrons and holes: S₁ + D(A) → D⁺(A⁻) + e⁻(h⁺) and S₁ + D⁺(A⁻) → D(A) + h⁺(e⁻). The quasi-stationary concentrations of charge carriers, the population of ionized impurity levels, and the energies of quasi-Fermi levels have been found as functions of light intensity and E_d, N_d (E_a, N_a). The values of rate constants that ensure the maximum quantum yield of conversion are discussed.

APPENDIX

Capture and Recombination in a Highly Doped Photoconductor

The method based on the conditions of detailed thermal equilibrium and rate equations for the concentrations of charge carriers and impurity levels is widely used in the kinetics of the photovoltaic effect [3–6]. This appendix summarizes the results related to the kinetic model discussed in the third section.

In an intrinsic photoconductor under constant optical pumping, quasi-steady-state concentrations of charge carriers obey the equation

$${{N}_{0}}W + I - \gamma np = 0,$$

(A)

where W is the rate constant, in s⁻¹, of electron–hole pair generation by thermal ionization of molecules in a crystal, I is the generation intensity [cm⁻³ s⁻¹] equal to the absorbed light intensity multiplied by the average absorption coefficient of solar light [cm⁻¹]; γ is the rate constant of bimolecular recombination [cm⁻³ s⁻¹]; and N₀ >> n, p is the concentration of molecules, electrons, and holes [cm⁻³], respectively.

Under thermal equilibrium conditions and in the absence of pumping (I = 0), the Fermi energy is introduced by the relations

$$\begin{gathered} \bar {n} = {{N}_{c}}\exp ( - \beta ({{E}_{c}} - {{E}_{F}})), \\ \bar {p} = {{N}_{{v}}}\exp ( - \beta ({{E}_{F}} - {{E}_{c}})), \\ \end{gathered} $$

(A2)

where N_c and N_v are the densities of states in the conduction and valence bands with energies E_c and E_v, respectively. For narrow bands typical of molecular crystals,

$${{N}_{c}} \approx {{N}_{{v}}} \approx {{N}_{0}}.$$

(A3)

Since the rate constant of thermal ionization obeys the Arrhenius law with activation energy equal to the band gap

$$\begin{gathered} W = {{W}_{0}}\exp ( - \beta \Delta ), \\ \Delta = {{E}_{c}} - E{}_{{v}},\,\,\,\,{{W}_{0}} \approx {{(2\pi \hbar \beta )}^{{ - 1}}} \\ \end{gathered} $$

(A4)

the Fermi energy in an intrinsic semiconductor is equal to the gap half-width

$${{E}_{F}} = {{({{E}_{c}} + {{E}_{{v}}})} \mathord{\left/ {\vphantom {{({{E}_{c}} + {{E}_{{v}}})} 2}} \right. \kern-0em} 2}.$$

(A5)

To find the solution to Eq. (A1), two quasi-Fermi levels that determine the quasi-stationary concentrations of electrons and holes under pumping conditions are introduced instead of E_F,

$$\begin{gathered} n = {{N}_{c}}\exp ( - \beta ({{E}_{c}} - {{E}_{{Fn}}})), \\ p = {{N}_{{v}}}\exp ( - \beta ({{E}_{{Fp}}} - {{E}_{c}})) \\ \end{gathered} $$

(A6)

and (A1) is converted into

$$\begin{gathered} \frac{{{{W}_{0}}}}{{\gamma {{N}_{0}}}} + \frac{{kI}}{{\gamma N_{0}^{2}}}\exp (\beta \Delta ) = \exp (\beta \eta ), \\ \eta = {{E}_{{Fn}}} - {{E}_{{Fp}}}. \\ \end{gathered} $$

(A7)

Equation (A7) shows that with increasing pumping, the distances between the quasi-levels increase logarithmically

$$\begin{gathered} \eta \approx \Delta + \beta \ln ({I \mathord{\left/ {\vphantom {I {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}), \\ {{I}_{0}}\exp ( - \beta \Delta ) < I < {{I}_{0}} = {{{{N}_{0}}{{W}_{0}}} \mathord{\left/ {\vphantom {{{{N}_{0}}{{W}_{0}}} k}} \right. \kern-0em} k}. \\ \end{gathered} $$

(A8)

For wide-gap photoconductors, in which ∆ ≥ 2 eV, Eq. (A8) is valid in the interval of I much larger than its variation under solar illumination conditions, 10¹⁶–10¹⁸ cm⁻² s⁻¹. The shift of the quasi-levels with increasing carrier concentration has the form

$$\begin{gathered} {{E}_{{Fn}}} = {{E}_{F}} + {{\beta }^{{ - 1}}}\ln ({n \mathord{\left/ {\vphantom {n {\bar {n}}}} \right. \kern-0em} {\bar {n}}}), \\ {{E}_{{Fp}}} = {{E}_{F}} - {{\beta }^{{ - 1}}}\ln ({p \mathord{\left/ {\vphantom {p {\bar {p}}}} \right. \kern-0em} {\bar {p}}}). \\ \end{gathered} $$

(A9)

In a photoconductor having one impurity state with a density N_d and an energy of E_v < E_d < E_c, two conditions of detailed thermal equilibrium between the impurity level and both bands are satisfied:

$$\begin{gathered} {{W}_{0}}n{}_{I}\exp ( - \beta ({{E}_{c}} - {{E}_{I}}) = {{\gamma }_{n}}\bar {n}({{N}_{I}} - {{n}_{I}}), \\ {{W}_{0}}({{N}_{I}} - {{n}_{I}})\exp ( - \beta ({{E}_{I}} - {{E}_{{v}}})) = {{\gamma }_{p}}{{n}_{I}}p, \\ \end{gathered} $$

(A10)

where ${{\bar {p}}_{d}}$ is the equilibrium concentration of ionized impurity levels and γ₁ is the rate constant of their bimolecular recombination with electrons (for localized impurities, γ_n ≈ γ_p ≈ γ/2). The band population is defined by Eqs. (A2), and that of the impurity level is determined by the Fermi distribution

$${{n}_{I}} = {{N}_{I}}\left( {1 + \frac{{{{\gamma }_{n}}}}{{{{\gamma }_{p}}}}\exp ( - \beta (E{}_{I} - E{}_{F})} \right),$$

(A11)

from which it follows that n_I/N_I = (1 + γ_n/γ_p)⁻¹ at E_F = E_I. When the Fermi level is above the impurity level, E_F > E_I , the equilibrium concentration of electrons is determined by ionization of the impurity

$$n\sim {{n}_{I}} \approx ({{{{\gamma }_{n}}} \mathord{\left/ {\vphantom {{{{\gamma }_{n}}} {{{\gamma }_{p}}}}} \right. \kern-0em} {{{\gamma }_{p}}}}){{N}_{I}}\exp ( - \beta ({{E}_{F}} - {{E}_{d}})).$$

(A12)

At constant light intensity, the concentrations are described by three balance equations

$$\begin{gathered} \dot {n} = I - \gamma np - {{\gamma }_{n}}n({{N}_{I}} - {{n}_{I}}) + {{W}_{0}}{{n}_{1}}\exp ( - \beta ({{E}_{c}} \\ - \,\,{{E}_{I}})),\,\,\,\,{{{\dot {n}}}_{I}} = {{\gamma }_{n}}n({{N}_{I}} - {{n}_{I}}) - {{W}_{0}}{{n}_{1}}\exp ( - \beta ({{E}_{c}} \\ - \,\,{{E}_{I}})) - {{\gamma }_{p}}{{n}_{1}}p + {{W}_{0}}({{N}_{I}} - {{n}_{I}})\exp ( - \beta ({{E}_{I}} - {{E}_{{v}}})), \\ \\ \dot {p} = I - \gamma np - {{\gamma }_{p}}{{n}_{1}}p + {{W}_{0}}({{N}_{I}} - {{n}_{I}}) \\ \times \,\,\exp ( - \beta ({{E}_{I}} - {{E}_{{v}}})) \\ \end{gathered} $$

(A13)

and the electroneutrality condition

$$n + n{}_{1} = p.$$

(A14)

Switching to dimensionless variables (12) transforms Eqs. (A13) and (A14) as

$$\begin{gathered} {{d{{y}_{1}}} \mathord{\left/ {\vphantom {{d{{y}_{1}}} {d\tau }}} \right. \kern-0em} {d\tau }} = 1 - {{\alpha }^{{ - 1}}}{{y}_{1}}{{y}_{3}} - {{y}_{1}}(1 - {{y}_{2}}) + {{Q}_{1}}{{y}_{2}}, \\ {{\alpha d{{y}_{2}}} \mathord{\left/ {\vphantom {{\alpha d{{y}_{2}}} {d\tau }}} \right. \kern-0em} {d\tau }} = {{y}_{1}}(1 - {{y}_{2}}) \\ - \,\,{{Q}_{1}}{{y}_{2}} - {{y}_{2}}{{y}_{3}} + {{Q}_{2}}(1 - {{y}_{2}}), \\ {{d{{y}_{3}}} \mathord{\left/ {\vphantom {{d{{y}_{3}}} {d\tau }}} \right. \kern-0em} {d\tau }} = 1 - {{y}_{2}}{{y}_{3}} + {{Q}_{2}}(1 - {{y}_{2}}), \\ \end{gathered} $$

(A15)

$${{y}_{1}} + \alpha {{y}_{2}} = {{y}_{3}}.$$

(A16)

Under quasi-stationary conditions (14) when α $\gg$ 1, Eq. (A15) is reduced to the algebraic equation

$$\begin{gathered} \alpha y_{2}^{3} - (\alpha + {{Q}_{1}} - {{Q}_{2}})y_{2}^{2} \\ - \,\,2(1 + {{Q}_{2}}){{y}_{2}} + 1 + {{Q}_{2}} = 0. \\ \end{gathered} $$

(A17)

In the three regions of variation of the parameters, approximate solutions to Eq. (A17) have the form

$${{y}_{2}} \approx \left\{ {\begin{array}{*{20}{c}} {{{{\left( {{{Q}_{1}} + \alpha } \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} - {{\left( {{{Q}_{1}} + \alpha } \right)} \mathord{\left/ {\vphantom {{\left( {{{Q}_{1}} + \alpha } \right)} 2}} \right. \kern-0em} 2},\,\,{{Q}_{1}} \gg \alpha ,\,\,{{Q}_{2}} = 0\,\,\,\,({\text{I}})} \\ {{{{({\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2})}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},\,\,\alpha \gg {{Q}_{1}},\,\,{{Q}_{2}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,({\text{II}})} \\ {1 - {{{\left( {2\alpha + {{Q}_{2}}} \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} + \alpha {{{\left( {2\alpha + {{Q}_{2}}} \right)}}^{{ - 1}}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,({\text{III}})} \end{array}} \right..$$

(A18)

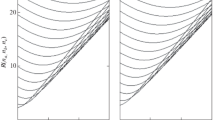
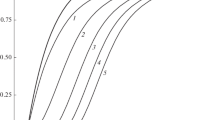
In low-population region I, where y₂ < $y_{2}^{*}$, thermal equilibrium is established between the impurity level and the conduction band. According to relation (A12), Q₁ exponentially depends on E_I, so that I corresponds to shallow electron traps, the population of which increases with increasing E_c − E_I. In intermediate region II, the population is constant, y₂ = $y_{2}^{*}$; i.e., it does not depend on energy (Q₁ or Q₂). In region II, thermal equilibrium between the bands is maintained by a constant population of traps, close to$y_{2}^{*}$ ≈ 1/2. In region III, the population is determined by the value of Q₂, y₂ > $y_{2}^{*}$. Equilibrium is established between the band and the highly populated impurity level, so that y₂ → 1 at Q₂ $\gg$ α. The dependence of population on the impurity level energy counted from the middle of the gap is shown in Fig. 1a. Expression (A12) relates the population to the energy of the quasi-Fermi level in regions I–III

$${{E}_{F}} \approx \left\{ {\begin{array}{*{20}{c}} {\frac{{{{E}_{c}} - {{E}_{I}}}}{2} + \frac{{{{k}_{B}}T}}{2}\ln \frac{I}{{\gamma {{N}_{0}}{{N}_{1}}}},\,\,\,\,({\text{I}})} \\ {{{E}_{I}} + \frac{{{{k}_{B}}T}}{2}\ln \frac{I}{{\gamma N_{1}^{2}}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,({\text{II}})} \\ {\frac{{{{E}_{I}} - {{E}_{v}}}}{2} - \frac{{{{k}_{B}}T}}{2}\ln \frac{I}{{\gamma {{N}_{0}}{{N}_{1}}}},\,\,\,\,({\text{III}})} \end{array}} \right..$$

(A19)

In regions I and III, the quasi-level is located in the intervals [E_I, E_c] and [E_v, E_I], so the concentration of majority carriers (electrons and holes, respectively) is determined by the thermal ionization of the impurity. Expression (A19) shows that dE_F/dE_I = 1/2 in regions I and III corresponds to thermal equilibrium between the corresponding band and the impurity level. The shift relative to the middle of the interval depends logarithmically on the density of states and light intensity. Figure 2a shows the dependence of the carrier concentration on E_I. In region II, the concentration of minority carriers (electrons) is much less than that of holes, and in low- and high-population regions I and III, the concentrations are comparable. In all the three regions, the shift depends on the pumping intensity in the same way, but the dependence on the concentration of impurity levels in region II differs from that in I and III.