Skip to main content
SpringerLink
Log in

Collapse of Capillary-Gravitational Waves and the Generation of Cumulative Jets

  • Published:
Fluid Dynamics Aims and scope Submit manuscript

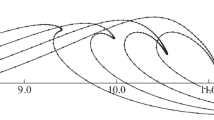
Abstract

In this paper, we study plane unsteady problems of motion of a free boundary in a potential flow of an ideal incompressible fluid. A numerical algorithm for calculating the shape of the free boundary is constructed based on the boundary-element method. When deriving approximations, the boundary smoothness is taken into account. The main attention is paid to the problems of the formation of thin cumulative jets and wave breaking, as well as substantiation of the reliability of numerical calculations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.

Similar content being viewed by others

REFERENCES

  1. Petrov, A.G., Quadrature formulas for periodic functions and their application to the boundary element method, Comput. Math. Math. Phys., 2008, vol. 48, no. 8, pp. 1266–1283.

    Article  MathSciNet  Google Scholar 

  2. Petrov, A.G., Analiticheskaya gidrodinamika (Analytical Hydrodynamics), Moscow: Fizmatlit, 2010.

  3. Baikov, N.D. and Petrov, A.G., Formation of a cumulative jet in the plane-parallel flow of a perfect fluid, Moscow Univ. Mech. Bull., 2017, vol. 72, no. 5, pp. 119–123.

    Article  Google Scholar 

  4. Baikov, N.D. and Petrov, A.G., Deformation of cylindrical cavities in plane-parallel potential flows with circulation and under the action of mass forces, Numer. Methods Program., 2018, vol. 19, pp. 207–214.

    Google Scholar 

  5. Karabut, E.A., Petrov, A.G., and Zhuravleva, E.N., Semi-analytical study of the Voinovs problem, Eur. J. Appl. Math., 2018, pp. 1–40. https://doi.org/10.1017/S0956792518000098

  6. Voinov, O.V. and Voinov, V.V., Numerical method of calculating nonstationary motions of an ideal incompressible fluid with free surfaces, Sov. Phys.-Dokl., 1975, vol. 20, no. 3, pp. 179–180.

    ADS  MATH  Google Scholar 

  7. Karabut, E.A. and Zhuravleva, E.N., Unsteady flows with a zero acceleration on the free boundary, J. Fluid Mech., 2014, vol. 754, pp. 308–331.

    Article  ADS  MathSciNet  Google Scholar 

  8. Peregrine, D.H., Breaking waves on beaches, Annu. Rev. Fluid Mech., 1983, vol. 15, pp. 149–178.

    Article  ADS  Google Scholar 

  9. Longuet-Higgins, M.S. and Cokelet, E.D., The deformation of steep surface waves on water. I. A numerical method of computation, Proc. R. Soc. London, Ser. A, 1976, vol. 350, pp. 1–26.

    Article  ADS  MathSciNet  Google Scholar 

  10. Petrov, A.G. and Smolyanin, V.G., Calculation of capillary-gravity wave contour on the surface of heavy liquid of finite depth, Vestn. Mosk. Univ., Ser. 1: Mat., Mech., 1991, no. 3, pp. 92–96.

  11. Petrov, A.G., The stability of capillary waves of finite amplitude, J. Appl. Math. Mech. (Engl. Transl.), 2017, vol. 81, no. 4, pp. 317–324.

  12. Lavrent'ev, M.A. and Shabat, B.V., Problemy gidrodinamiki i ikh matematicheskie modeli (Hydrodynamics Problems and their Mathematical Models), Moscow: Nauka, 1977.

Download references

Funding

This work is supported by the state assignment, state registration no. AAAA-A20-120011690138-6.

Author information

Authors and Affiliations

  1. Moscow State University, 119991, Moscow, Russia

    N. D. Baykov

  2. Ishlinsky Institute for Problems in Mechanics, Russian Academy of Sciences, 119526, Moscow, Russia

    A. G. Petrov

Authors
  1. N. D. Baykov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. G. Petrov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to N. D. Baykov or A. G. Petrov.

Additional information

Translated by A. Ivanov

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Baykov, N.D., Petrov, A.G. Collapse of Capillary-Gravitational Waves and the Generation of Cumulative Jets. Fluid Dyn 55, 953–964 (2020). https://doi.org/10.1134/S0015462820080030

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0015462820080030

Keywords:

Search

Navigation