Abstract
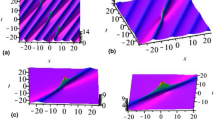
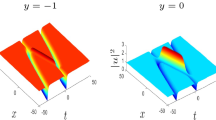
The features of the interaction between internal solitary waves are investigated within the framework of the completely integrable Gardner equation with positive cubic nonlinearity. It is shown that the soliton polarity affects radically the result of the interaction between the solitons. The role of the pair interactions between solitons of different polarities proceeding when rogue waves emerge in the soliton fields in a stratified basin is demonstrated. The effect of such interactions on the higher-order moments of the wave field is studied.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Yu. Z. Miropol’skii, Dynamics of Internal GravityWaves in the Ocean (Gidrometeoizdat, Leningrad, 1981) [in Russian].
T. Kakutani and N. Yamasaki, “Solitary Waves on a Two-Layer Fluid,” J. Phys. Soc. Japan 45, 674–679 (1978).
C. Koop and G. Butler, “An Investigation of Internal SolitaryWaves in a Two-Fluid System,” J. FluidMech. 112, 225–251 (1981).
P. Guyenne, “Large-Amplitude Internal Solitary Waves in a Two-Fluid Model,” C.R. Mecanique, 334–341 (2006).
W. Choi and R. Camassa, “Fully Nonlinear Internal Waves in a Two-Fluid System,” J. Fluid Mech. 396, 1–36 (1999).
M. Funakoshi and M. Oikawa, “Long Internal Waves of Large Amplitude in a Two-Layer Fluid,” J. Phys. Soc. Japan 55, 128–144 (1986).
J. A. Knauss, Introduction to Physical Oceanography (Prentice Hall, 1996).
R. Grimshaw, E. Pelinovsky, and T. Talipova, “Modeling Internal Solitary Waves in the Coastal Ocean,” Surveys in Geophysics 28, 273–298 (2007).
R. Grimshaw, E. Pelinovsky, T. Talipova, and A. Sergeeva, “Rogue InternalWaves in the Ocean: LongWave Model,” Eur. Phys. J. Spec. Top. 185, 195–208 (2010).
E. N. Pelinovsky and A. V. Slunyaev, “Generation and Interaction of Large-Amplitude Solitons,” Pis’ma v Zh. Eksp. Teor. Fiz. 67, 628–633 (1998).
A. V. Slunyaev and E. N. Pelinovsky, “Dynamics of Large-Amplitude Solitons,” Zh. Eksp. Teor. Fiz. 116, 318–335 (1999).
A. V. Slunyaev, “Dynamics of Large-Amplitude Localized Waves in a Weakly Dispersive Medium with Quadratic and Cubic Nonlinearity,” Zh. Eksp. Teor. Fiz. 119, 606–612 (2001).
E. G. Shurgalina and E. N. Pelinovsky, “Nonlinear Dynamics of a Soliton Gas: Modified Korteweg-de Vries Equation Framework,” Phys. Lett. A 380 (24), 2049–2053 (2016).
R. Grimshaw, E. Pelinovsky, T. Talipova, and O. Kurkina, “Internal SolitaryWaves: Propagation, Deformation, and Disintegration,” Nonlinear Processes in Geophysics 17 (6), 633–649 (2010).
R. Grimshaw, “Internal Solitary Waves (Chapter 1),” in: R. Grimshaw (Ed.), Environmental Stratified Flows (Kluwer Academic Publishers, Dordrecht, The Netherlands, 2001), pp. 1–28.
E. N. Pelinovsky, O. E. Polukhina, and K. Lamb, “Nonlinear Internal Waves in Ocean Stratified in Density and Flow,” Okeanologiya 40 (6), 805–815 (2000).
T. G. Talipova, E. N. Pelinovsky, K. Lamb, R. Grimshaw, and P. Holloway, “Effects of Cubic Nonlinearity in Propagation of Intense InternalWaves,” Dokl. Akad. Nauk SSSR 364 (6), 824–827 (1996).
E. N. Pelinovsky, E. G. Shurgalina, A. V. Sergeeva, T. G. Talipova, G. A. El, and R. H. J. Grimshaw, “Two-Soliton Interaction as an Elementary Act of Soliton Turbulence in Integrable Systems,” Phys. Lett. A 377, Nos. 3–4, 272–275 (2013).
E. N. Pelinovsky and E. G. Shurgalina, “Two-Soliton Interaction within the Framework of the Modified Korteweg-de Vries Equation,” Izv. Vuzov. Radiofizika 57 (10), 825–833 (2014).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © E.G. Shurgalina, 2018, published in Izvestiya Rossiiskoi Akademii Nauk, Mekhanika Zhidkosti i Gaza, 2018, No. 1, pp. 61–67.
Rights and permissions
About this article
Cite this article
Shurgalina, E.G. Mechanism of the Emergence of Rogue Waves As a Result of the Interaction between Internal Solitary Waves in a Stratified Basin. Fluid Dyn 53, 59–64 (2018). https://doi.org/10.1134/S0015462818010123
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0015462818010123