Abstract
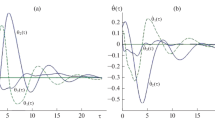
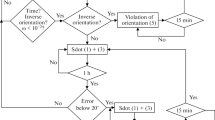
The stabilization of the relative equilibrium of a satellite moving in a circular orbit, which is equipped with magnetic orientation system. It is shown that the linearized system of equations of motion belongs to a special class of linear time-varying systems, reducible to time-invariant ones. For obtained time-invariant system, controllability is analyzed, and the optimal stabilization algorithm based on the LQR method is constructed. The results of numerical simulation demonstrate the efficiency of the proposed approach.






Similar content being viewed by others
REFERENCES
Pittelkau, M.E., Optimal periodic control for spacecraft pointing and attitude determination, J. Guid. Control Dyn., 1993, vol. 16, no. 6, pp. 1078–1084.
Arduini, C. and Baiocco, P., Active magnetic damping attitude control for gravity gradient stabilized spacecraft, J. Guid. Control Dyn., 1997, vol. 20, no. 1, pp. 117–122.
Psiaki, M., Magnetic torque attitude control via asymptotic periodic linear quadratic regulation, J. Guid. Control Dyn., 2001, vol. 24, no. 2, pp. 386–304.
Lovera, M., De Marchi, E., and Bittanti, S., Periodic attitude control techniques for small satellites with magnetic actuators, IEEE Trans. Control Syst. Technol., 2002, vol. 10, no. 1, pp. 90–95.
Lovera, M. and Astolfi, A., Spacecraft attitude control using magnetic actuators, Automatica, 2004, vol. 40, pp. 1405–1414.
Lovera, M. and Astolfi, A., Global magnetic attitude control of spacecraft in the presence of gravity gradient, IEEE Trans. Aerosp. Electron. Syst., 2006, vol. 12, pp. 796–805.
Rehanoglu, M. and Hervas, J.R., Three-axis magnetic attitude control algorithm for small satellites, in Proc. of the 5th Int. Conf. on Recent Advance Technologies, Istanbul, 2011, pp. 897–902.
Rodriquez-Vazquez, A.L., Martin-Prats, M.A., and Bernelli-Zazzera, F., Spacecraft magnetic attitude control using approximating sequence Riccati equations, IEEE Trans. Aerosp. Electron. Syst., 2015, vol. 51, no. 4, pp. 3374–3385.
Ovchinnikov, M.Yu., Roldugin, D.S., Ivanov, D.S., and Penkov, V.I., Choosing control parameters for three axis magnetic stabilization in orbital frame, Acta Astronaut., 2015, vol. 116, pp. 74–77.
Ovchinnikov, M.Yu., Pen’kov, V.I., Roldugin, D.S., and Ivanov, D.S., Magnitnye sistemy orientatsii malykh sputnikov (Magnetic Attitude Control Systems for Small Satellites), Moscow: IPM im. M.V. Keldysha, 2016. https://doi.org/10.20948/mono-2016-ovchinnikov
Ivanov, D.S., Ovchinnikov, M.Yu., Penkov, V.I., et al., Advanced numerical study of the three-axis magnetic attitude control and determination with uncertainties, Acta Astronaut., 2017, vol. 132, pp. 103–110.
Zhou, K., Huang, H., Wang, X., and Sun, L., Magnetic attitude control for Earth-pointing satellites in the presence of gravity gradient, Aerosp. Sci. Technol., 2016, vol. 60, pp. 115–123. https://doi.org/10.1016/j.ast.2016.11.003
Sutherland, R., Kolmanovsky, I.K., and Girard, A.R., Attitude control of a 2U cubesat by magnetic and air drag torques, IEEE. Trans.Control Syst. Technol., 2017.
Ovchinnikov, M.Yu. Penkov, V.I., et al., Geomagnetic field models for satellite angular motion studies, Acta Astronaut., 2018, vol. 144, pp. 171–180. https://arxiv.org/ pdf/1707.04959.pdf
Dipak, G., Bijoy, M., Bidul, T.N., and Manoranjan, S., Three-axis global magnetic attitude control of Earth-pointing satellites in circular orbit, Asian J. Control, 2017, vol. 19, no. 6, pp. 2028–2041. https://doi.org/10.1002/asjc.1506
Yang, H., Spacecraft attitude and reaction wheel desaturation combined control method, IEEE Trans. Aerosp. Electron. Syst., 2017, vol. 53, no. 1, pp. 286–295.
Kim, J., Jung, Y., and Bang, H., Linear time-varying model predictive control of magnetically actuated satellites in elliptic orbits, Acta Astronaut., 2018, vol. 151, pp. 791–804.
Yang, Y., Spacecraft Modeling, Attitude Determination, and Control: Quaternion-Based Approach, New York: CRC Press, Taylor & Francis Group, 2019.
Silani, E. and Lovera, M., Magnetic spacecraft attitude control: A survey and some new results, Control Eng. Practice, 2005, vol. 13, pp. 357–371.
Sofyalı, A., Jafarov, E.M., and Wisniewski, R., Robust and global attitude stabilization of magnetically actuated spacecraft through sliding mode, Aerosp. Sci. Technol., 2018, vol. 76, pp. 91–104. https://doi.org/10.1016/j.ast.2018.01.022
Bhat, S.P., Controllability of nonlinear time-varying systems: Application to spacecraft attitude control using magnetic actuation, IEEE Trans. Autom. Control, 2005, vol. 50, no. 11, pp. 1725–1735.
Yang, Y., Controllability of spacecraft using only magnetic torques, IEEE Trans. Aerosp. Electron. Syst., 2016, vol. 52, no. 2, pp. 955–962.
Beletskii, V.V., Dvizhenie iskusstvennogo sputnika otnositel’no tsentra mass (Artificial Satellite Motion Relative to Center of Mass), Moscow: Nauka, 1965.
Wertz, J., Spacecraft Attitude Determination and Control, Dordrecht: D. Reidel, 1978.
Kalenova, V.I. and Morozov, V.M., Lineinye nestatsionarnye sistemy i ikh prilozheniya k zadacham mekhaniki (Linear Time-Varying Systems and Their Applications to Problems of Mechanics), Moscow: Fizmatlit, 2010.
Kalenova, V.I. and Morozov, V.M., The reducibility of linear second-order time-varying systems with control and observation, J. Appl. Math. Mech., 2012, vol. 76, no. 4, pp. 413–422.
Kalenova, V.I. and Morozov, V.M., On the control of linear time-varying systems of a special form, J. Comput. Syst. Sci. Int., 2013, vol. 52, no. 3, pp. 333–341.
Bellman, R., Introduction to Matrix Analysis, New York: McGraw-Hill, 1960; Moscow: Nauka, 1969.
Laub, A.J. and Arnold, W.F., Controllability and observability criteria for multivariable linear second order models, IEEE Trans. Autom. Control, 1984, vol. AC-29, no. 2, pp. 163–165.
Krasovskii, N.N., Teoriya upravleniya dvizheniem. Lineinye sistemy (Theory of Motion Control. Linear Systems), Moscow: Nauka, 1968.
Roitenberg, Ya.N., Avtomaticheskoe upravlenie (Automatic Control), Moscow: Nauka, 1978.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by V. Arutyunyan
Rights and permissions
About this article
Cite this article
Morozov, V.M., Kalenova, V.I. Satellite Control Using Magnetic Moments: Controllability and Stabilization Algorithms. Cosmic Res 58, 158–166 (2020). https://doi.org/10.1134/S0010952520030041
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0010952520030041