Abstract
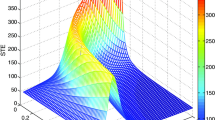
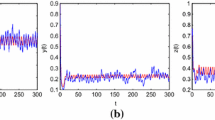
We present a mathematical model of a population developing while consuming polluting substances that negatively affect individual reproduction. We describe equations of the model and study the properties of model solutions, including existence and stability of equilibrium points. We give the results of a numerical experiment that shows that it is possible to control the population size by changing the rate with which polluting substances are introduced into the environment.
Similar content being viewed by others
References
Poluektov, R.A., Pykh, Yu.A., and Shvytov, I.A., Dinamicheskie modeli ekologicheskikh sistem (Dynamic Models of Ecological Systems), Leningrad: Gidrometeoizdat, 1980.
Fedorov, V.D. and Gil’manov, T.G., Ekologiya (Ecology), Moscow: Mosk. Gos. Univ., 1980.
Svirezhev, Yu.M., Nelineinye volny, dissipativnye struktury i katastrofy v ekologii (Nonlinear Waves, Dissipative Structures, and Catastrophes in Ecology), Moscow: Nauka, 1987.
Krestin, S.V. and Rozenberg, G.S., One Mechanism of the Flowering of Water in a Plain-Type Reservoir, Biophysics, 1996, vol. 41, no. 3, pp. 650–654.
Il’ichev, V.G., Delta Functions and the Investigation of Volterra Ecological Models in a Changing Environment, Izv. Vyssh. Uchebn. Zaved., Mat., 1998, vol. 42, no. 4, pp. 23–33.
Abrosov, N.S., Ecological Factors and the Mechanisms of Forming the Species Diversity in Ecosystems and the Problem of Species Compatibility, in Ekologiya v Rossii na rubezhe XXI v (Ecology in Russia on the Turn of the XXI Century), Moscow: Nauchnyi Mir, 1999, pp. 54–69.
Bibik, Yu.V., Popov, S.V., and Sarancha, D.A., Neavtonomnye matematicheskie modeli ekologicheskikh sistem (Non-autonomous Mathematical Models of Ecological Systems), Moscow: Vychisl. Tsentr Ross. Akad. Nauk, 2004.
Novosel’tsev, V.N., Natural Organism Technologies and Polonium-210 Poisoning, in Proc. of the 4th International Conference on Control Problems, Proc. of the Institute of Control Sciences of the RAS, 2009, section S.2 “Control theory in interdisciplinary medical-biological studies,” pp. 884–892.
Pichugina, A.N., An Integrodifferential Model of a Population under the Effects of Pollutants, Sib. Zh. Ind. Mat., 2004, vol. 7, no. 4, pp. 130–140.
Pertsev, N.V., Tsaregorodtseva, G.E., and Pichugina, A.N., Stability Analysis for Equilibrium Points of One Model of Population Dynamics, Vestn. Omsk. Univ., 2009, no. 2, pp. 46–49.
Pontryagin, L.S., Obyknovennye differentsial’nye uravneniya (Ordinary Differential Equations), Moscow: Nauka, 1974.
Krasnosel’skii, M.A., Polozhitel’nye resheniya operatornykh uravnenii (Positive Solutions of Operator Equations), Moscow: Fizmatgiz, 1962.
Krasnosel’skii, M.A., Vainikko, G.M., Zabreiko, P.P., et al., Priblizhennoe reshenie operatornykh uravnenii (Approximate Solution of Operator Equations), Moscow: Nauka, 1969.
Barbashin, E.A., Vvedenie v teoriyu ustoichivosti (Introduction to Stability Theory), Moscow: Nauka, 1967.
Obolenskii, A.Yu., On the Stability of Solutions for Autonomous Vazhevski Systems with Delays, Ukr. Mat. Zh., 1983, vol. 35, no. 5, pp. 574–579.
D’eri, I. and Pertsev, N.V., On the Stability of Equilibrium Points for Functional-Differential Equations with Delays That Possess the Mixed Monotonicity Property, Dokl. Akad. Nauk SSSR, 1987, vol. 297, no. 1, pp. 23–25.
Gantmakher, F.R., Teoriya matrits (Theory of Matrices), Moscow: Nauka, 1966. Translated into English under the title Theory of Matrices, New York: Chelsea, 1959.
Coddington, E.A. and Levinson, N., Theory of Ordinary Differential Equations, New York: McGraw-Hill, 1955.
D’yakonov, V.P., Matlab 6/6.1/6.5 + Simulink 4/5 v matematike i modelirovanii. Polnoe rukovodstvo pol’zovatelya (Matlab 6/6.1/6.5 + Simulink 4/5 in Mathematics and Modeling. A Complete User’s Guide), Moscow: SOLON-Press, 2003.
Romanovskii, Yu.M., Stepanova, N.V., and Chernavskii, D.S., Matematicheskaya biofizika (Mathematical Biophysics), Moscow: Nauka, 1984.
Author information
Authors and Affiliations
Additional information
Original Russian Text © N.V. Pertsev, G.E. Tsaregorodtseva, 2011, published in Avtomatika i Telemekhanika, 2011, No. 1, pp. 141–153.
Rights and permissions
About this article
Cite this article
Pertsev, N.V., Tsaregorodtseva, G.E. Modeling population dynamics under the influence of harmful substances on the individual reproduction process. Autom Remote Control 72, 129–140 (2011). https://doi.org/10.1134/S0005117911010115
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0005117911010115