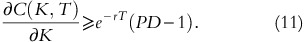INTRODUCTION

Arbitrage-free valuation is a fundamental principle in the modern theory of financial asset pricing. Hence, establishing static arbitrage bounds is essential for both academicians and practitioners. For example, Dixit et al (2009) examine whether lower-bound violations occur in empirical data.

In the field of derivative pricing, an arbitrage-free surface is necessary for pricing illiquid exotic derivatives with arbitrary payoffs and copula-based pricing of multi-asset products. For example, using the implied risk-neutral density, Monteiro et al (2011) accurately price European-style binary options, Benaim et al (2008) calculate the convexity correction for constant maturity swaps, and Cherubini and Luciano (2002) price bivariate equity options. Moreover, although interpolation performed in the implied volatility space has several advantages (see for example Figlewski (2009) and Orosi (2012)), the resulting call option surface is not arbitrage-free. To generate a suitable call option surface from an implied volatility surface, Fengler (2009) and Orosi (2014a, 2014b) employ arbitrage-free interpolants.

Typically, in the absence of call spread, butterfly spread and calendar spread arbitrage, discrete sets of call option prices are considered to be free of static arbitrage (see for example Aït-Sahalia and Duarte (2003) and Carr and Madan (2005)). Moreover, similar conditions can be derived for a continuous call price surface to be free of static arbitrage (see for example Fengler and Hin (2013) and Roper (2010)). However, these results make certain assumptions about the underlying process, and are not applicable to the case when there is a positive probability of default.

In this work, we derive an improved lower bound for European-style put options written on defaultable assets, which is necessary for the construction of an arbitrage-free put option surface. Furthermore, two additional no-arbitrage conditions are established, one for puts and one for calls, which are tighter than the ones commonly reported in current literature. An immediate implication of our results is that in the presence of default, the commonly stated no-arbitrage conditions required to generate an arbitrage-free call or put option surface are not always sufficient.

ASSUMPTIONS AND NOTATION

Utilizing Merton (1973) as a guide, the following assumptions are made: (i) capital markets are perfect; (ii) there is no arbitrage; (iii) investors have positive marginal utility of wealth; and (iv) current and future interest rates are strictly positive. In addition, we assume that the stock becomes worthless in the case of default. Based on these conditions, consider a stock that has a current price of S0 and a price of S T at some time in the future T. Denoting the risk-neutral probability of default before some time T by PD and the risk-neutral survival probability of the asset before time T by P(S T >0), the following holds:

Moreover, let C(K, T), P(K, T), B call (K, T) and B put (K, T) be, respectively, the current prices of a European call, European put, European binary call and European binary put options on the stock with strike K, maturity T. By employing the well-known relationships between European-style calls and puts and European binaries, we have:

and the risk-neutral probability of default and survival probability can be expressed as:

and

Based on the above equations, the price of the digital contract, D(T), that pays a unit currency if default happens before time T and zero otherwise is given by:

Therefore, D(T) can be replicated by call options and cash as follows:

and by put options as follows:

GENERAL RESULTS

 

Proposition 1:

  • The lower bound of a European put option written on a defaultable asset is

where D is the present value of future dividends expected to be paid before T.

Proof Orosi (2014b) shows that the lower bound of a European call option written on a defaultable asset is

Moreover, the put–call parity relation can be rearranged as follows:

Substituting (9) into the above gives

 □

Proposition 2:

  • The lower bound of the first derivative of a European put option written on a defaultable asset is

Proof Assume otherwise and form the following zero-value portfolio at time zero:

where B represents the amounts invested in bonds. In the case of default, the value of the portfolio at the time of expiry is given by:

because the payoff of B put (K, T)=1 and D(T)=1. If the asset does not default before expiry and the option finishes in the money (or S T ⩽K equivalently), then the value of the portfolio at the time of expiry is given by:

because the payoff of B put (K, T)=1 and D(T) becomes worthless. Finally, if the asset does not default before expiry and the option does not finish in the money (or S T >K equivalently), then the value of the portfolio at the time of expiry is given by:

and B put (K, T) and D(T) become worthless. Therefore, if (10) does not hold, a portfolio can be constructed that yields static arbitrage violation. □

Proposition 3:

  • The lower bound of the first derivative of a European call option written on a defaultable asset is

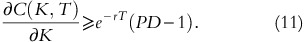
Proof Differentiating the put–call parity relation

with respect to K yields

which can be written using (2) and (3) as

Rearranging and then substituting (6) gives:

DISCUSSION AND FUTURE RESEARCH

The commonly stated no-arbitrage constraints on European-style option price surfaces are derived under the premise that the underlying security stays strictly positive. In this section, we point out that if the option implied risk-neutral probabilities of default, as shown in (4) and (5), are strictly positive, these constraints become tighter. Hence, if conditions (8), (9), (10) and (11) are ignored when fitting an arbitrage-free option surface to certain market quotes, which imply a positive probability of default, arbitrage violations can occur even if the commonly stated arbitrage conditions are not violated. The implications of condition (9) have been discussed in Orosi (2014b), therefore we will direct our attention to the other three conditions.

First of all, it should be noted that, assuming PD>0, (8) is higher for strike prices for which

than Merton’s lower bound of

Although most financial engineering applications utilize an arbitrage-free call option surface, in some cases using an arbitrage-free put option surface is preferable. For example, Monnier (2013) extracts risk-neutral densities from a set of arbitrage-free put option prices.

Moreover, (10) and (11) are also higher than the typically stated lower bounds of (∂P(K, T))/(∂K)⩾0 and (∂C(K, T))/(∂K)⩾−e−rT as long as PD>0. Although these two conditions are not always required for the construction of an arbitrage-free option surface, they are commonly stated in the literature (see for example Aït-Sahalia and Duarte (2003), Fengler (2009), Monnier (2013) and Orosi (2011)).

Another important implication of our finding is that all four improved lower bounds can be used to test the efficiency of option markets by examining whether arbitrage violations occur in market data. For example, Dixit et al (2009) find that lower-bound violations and arbitrage opportunities do occur in the S&P CNX Nifty Index option market.

CONCLUSION

In this work, we derive three new improved lower bounds for European-style call and put options written on defaultable assets. We demonstrate that these bounds are tighter than the commonly stated lower bounds and briefly discuss the implications of our results.