Abstract
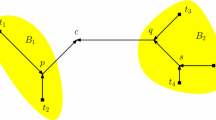
By the local optimal Steiner tree is meant a tree with optimally distributed Steiner points for a given adjacency matrix. The adjacency matrix defines the point of local minimum, and all arrangements (coordinates) of the Steiner points that are admissible for it define the minimum neighborhood. Solution is local optimal if the tree length cannot be reduced by rearranging the Steiner points. An algorithm of local optimization based on the concept of coordinatewise descent was considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
Lotarev, D.T. and Uzdemir, A.P., Arrangement of the Transport Networks over a Heterogeneous Territory, Avtom. Telemekh., 2002, no.7, pp. 114–124.
Gordeev, E.N. and Tarastsov, O.G., Steiner Problem. A Review, Diskretn. Mat., 1993, vol.5, no. 2, pp. 3–28.
Courant, R. and Robbins, H., What is Mathematics?, London: Oxford Univ. Press, 1941. Translated under the title Chto takoe matematika?, Moscow: Prosveshchenie, 1967.
Nutenko, V. Ya., Ispol'zovanie problemy Shteinera i ee obobshchenii dlya resheniya nekotorykh zadach prostranstvennoi ekonomiki (Using the Steiner Problem and Its Generalizations to Solve Some Problems of Spatial Economics), Moscow: Tsentr. Econom. Mat. Inst., 1968.
Garey, M.L. and Johnson, D.S., Computers and Intractability: A Guide to the Theory of NP-Completness, San Francisco: Freeman, 1979. Translated under the title Vychislitel'nye machiny i trudnoreshaemye zadachi, Moscow: Mir, 1982.
Emelichev, V.A., Mel'nikov, O.I., Sarvanov, V.I., et al., Lektsii po teorii grafov (Lectures on the Graph Theory), Moscow: Nauka, 1990.
Rights and permissions
About this article
Cite this article
Lotarev, D.T., Suprun, A.V. & Uzdemir, A.P. Local Optimization in the Steiner Problem on the Euclidean Plane. Automation and Remote Control 65, 1089–1098 (2004). https://doi.org/10.1023/B:AURC.0000038715.76668.83
Issue Date:
DOI: https://doi.org/10.1023/B:AURC.0000038715.76668.83