Abstract
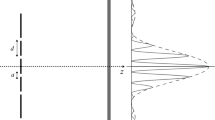
The probability pattern emerging in two-slit experiments is a typical quantum feature whose essential ingredients are examined by translating them into the spin-\( \frac{1}{2} \) formalism. In view of the existence of extensions of quantum theory preserving some classical structure, we discuss how the two-slit probabilities behave under such extensions. We consider a generalization of the standard classical probability theory, to be called operational probability theory, that turns out to host the so called quantum probabilities.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
E. G. Beltrametti and S. Bugajski, “A classical extension of quantum mechanics,” J. Phys. A: Math. Gen. 28, 3329–3343 (1995).
E. G. Beltrametti and S. Bugajski, “The Bell phenomenon in classical frameworks,” J. Phys. A: Math. Gen. 29, 247–261 (1996).
G. C. Rota, “Twelve problems in probability no one likes to bring up,” in The Fubini Lectures (University of Torino, 1998).
E. G. Beltrametti and G. Cassinelli, The Logic of Quantum Mechanics (Addison-Wesley, Reading, Massachusetts, 1981).
G. Cassinelli and N. Zanghi, “Conditional probabilities in quantum mechanics. I.__Conditioning with respect to a single event,” Nuovo Cimento B 73, 237–245 (1983); “Conditional probabilities in quantum mechanics. II.–– Additive conditional probabilities,” Nuovo Cimento B 79, 141–154 (1984).
B. Misra, “On a new definition of quantal states,” in Physical Reality and Mathematical Description, C. P. Enz and J. Mehra, eds. (Reidel, Dordrecht, 1974).
S. Bugajski, “Delinearization of quantum logic,” Int. J. Theor. Phys. 32, 389–398 (1993).
E. G. Beltrametti and S. Bugajski, “Effect algebras and statistical physical theories,” J. Math. Phys. 38, 3020–3030 (1997).
E. G. Beltrametti and S. Bugajski, “Quantum mechanics and operational probability theory,” Found. Sci., to appear.
S. Bugajski, “Fundamentals of fuzzy probability theory,” Int. J. Theor. Phys. 35, 2229–2244 (1996).
S. Bugajski, K. E. Hellwig, and W. Stulpe, “On fuzzy random variables and statistical maps,” Rep. Math. Phys. 41, 1–11 (1998).
S. Gudder, “Fuzzy probability theory,” Demonstratio Mathematica 31, 235–354 (1998).
E.B. Davies and J. T. Lewis, “An operational approach to quantum probability,” Comm. Math. Phys. 17, 239–260 (1970).
B. Mielnik, “Geometry of quantum states,” Comm. Math. Phys. 9, 55–80 (1968).
B. Mielnik, “Theory of filters,” Comm. Math. Phys. 15, 1–46 (1969).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Beltrametti, E.G., Bugajski, S. Remarks on Two-Slit Probabilities. Foundations of Physics 30, 1415–1429 (2000). https://doi.org/10.1023/A:1026401800614
Issue Date:
DOI: https://doi.org/10.1023/A:1026401800614