Skip to main content
SpringerLink
Log in

On Quantum Chaos and Maass Waveforms of CM-Type

  • Published:
Foundations of Physics Aims and scope Submit manuscript

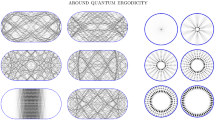
Abstract

In this paper, we report on some machine experiments which suggest that waveforms of CM-type are asymptotically Gaussian-distributed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

REFERENCES

  1. M. Gutzwiller, “Physics and Selberg's trace formula,” in The Selberg Trace Formula and Related Topics, D. Hejhal, P. Sarnak, and A. Terras, eds. (Contemp. Math., Vol. 53) (Amer. Math. Soc., 1986), pp. 215-251.

  2. M. Gutzwiller, Chaos in Classical and Quantum Mechanics (Springer, 1990).

  3. V. Arnold, Mathematical Methods of Classical Mechanics (Springer, 1978), pp. 246, 313-314.

  4. E. Hopf, Ergodentheorie (Springer, 1937), Chap. 5 and pp. 28-30.

  5. D. A. Hejhal, “On eigenfunctions of the Laplacian for Hecke triangle groups,” in Emerging Applications of Number Theory, D. Hejhal, J. Friedman, M. Gutzwiller, and A. Odlyzko, eds. (IMA, Vol. 109) (Springer-Verlag, 1999), pp. 291-315.

  6. T. Miyake, Modular Forms (Springer, 1989).

  7. I. M. Gelfand, M. I. Graev, and I. I. Pyatetskii-Shapiro, Representation Theory and Automorphic Functions (Saunders, 1969).

  8. R. Fricke and F. Klein, Vorlesungen über die Theorie der automorphen Funktionen, Vol. 1 (Teubner, Leipzig, 1897).

    Google Scholar 

  9. D. A. Hejhal and B. Rackner, “On the topography of Maass waveforms for PSL(2, Z),” Exper. Math. 1, 275-305 (1992).

    Google Scholar 

  10. R. Aurich and F. Steiner, “Statistical properties of highly excited quantum eigenstates of a strongly chaotic system,” Physica D 64, 185-214 (1993). See also Physica D 48, 445-470 (1991).

    Google Scholar 

  11. R. Aurich, A. Bäcker, R. Schubert, and M. Taglieber, “Maximum norms of chaotic quantum eigenstates and random waves,” Physica D 129, 1-14 (1999).

    Google Scholar 

  12. M. V. Berry, “Regular and irregular semiclassical wavefunctions,” J. Phys. A 10, 2083-2091 (1977).

    Google Scholar 

  13. D. A. Hejhal, The Selberg Trace Formula for PSL(2, ℝ), Vol. 2 (Lecture Notes in Mathematics, Vol. 1001) (Springer, 1983).

  14. R. Salem and A. Zygmund, “Some properties of trigonometric series whose terms have random signs,” Acta Math. 91, 245-301 (1954).

    Google Scholar 

  15. A. Erdélyi, Higher Transcendental Functions, Vol. 2 (McGraw-Hill, 1953).

  16. P. Sarnak, “Arithmetic quantum chaos,” Israel Math. Conf. Proc. 8, 183-236 (1995).

    Google Scholar 

  17. W. Luo and P. Sarnak, “Quantum ergodicity of eigenfunctions on PSL(2, ℤ)\H,” Publ. Math. IHES 81, 207-237 (1995), especially Corollary 1.3.

    Google Scholar 

  18. H. Maass, “Über eine neue Art von nichtanalytischen automorphen Funktionen und die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen,” Math. Ann. 121, 141-183 (1949), especially Eqs. (29) and (101).

    Google Scholar 

  19. H. Iwaniec and P. Sarnak, “Perspectives on the analytic theory of L-functions,” preprint, 2000.

  20. P. Sarnak, “Estimates for Rankin-Selberg L-functions and quantum unique ergodicity,” preprint, 2000.

  21. E. Hecke, Mathematische Werke (Vandenhoeck and Ruprecht, Göttingen, 1959), pp. 441(15), 623(top), 705(49), 718(middle).

    Google Scholar 

  22. G. Shimura and Y. Taniyama, Complex Multiplication of Abelian Varieties and Its Applications to Number Theory (Publ. Math. Soc. Japan, No. 6, 1961), Sec. 18.

    Google Scholar 

  23. Y. Taniyama, “L-functions of number fields and zeta functions of abelian varieties,” J. Math. Soc. Japan 9, 330-366 (1957).

    Google Scholar 

  24. A. Weil, “On a certain type of characters of the ide- le-class group of an algebraic number field,” in Proceedings of the International Symposium on Algebraic Number Theory (Tokyo-Nikko, Science Council of Japan, 1955), pp. 1-7.

    Google Scholar 

  25. D. Bump, Automorphic Forms and Representations (Cambridge University Press, 1996).

  26. H. Cohn, Advanced Number Theory (Dover, 1980), pp. 33(5a), 35, 45-49, 99-101, 131-136, 142, 185, 187 bottom, 194, 271.

  27. W. Narkiewicz, Elementary and Analytic Theory of Algebraic Numbers, 2nd edn. (Springer, 1990), pp. 43, 94-97, 110-112, 341, 343, 437(top), 457.

  28. E. Hecke, “Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen,” Math. Z. 1, 357-376 (1918); 6, 11-51 (1920).

    Google Scholar 

  29. D. A. Hejhal and S. Arno, “On Fourier coefficients of Maass waveforms for PSL(2, ℤ),” Math. Comp. 61, 245-267 and S11-S16 (1993).

    Google Scholar 

  30. J. P. Serre, Abelian ℓ-Adic Representations and Elliptic Curves (Benjamin, 1968), pp.I18-I29.

  31. F. Shahidi, “Symmetric power L-functions for GL(2),” in Elliptic Curves and Related Topics, H. Kisilevsky and M. R. Murty, eds. (CRM Proceedings, No. 4) (Amer. Math. Soc., 1994), pp. 159-182.

  32. R. A. Rankin, “Fourier coefficients of cusp forms,” Math. Proc. Cambridge Phil. Soc. 100, 5-29 (1986).

    Google Scholar 

  33. A. Selberg, On the estimation of Fourier coefficients of modular forms, Proc. Symp. Pure Math. 8, 1-15 (1965), especially Eqs. (1.14) and (2.16).

    Google Scholar 

  34. A. E. Ingham, “Some asymptotic formulae in the theory of numbers,” J. London Math. Soc. 2, 202-208 (1927), especially p. 202(middle).

    Google Scholar 

  35. B. M. Wilson, “Proofs of some formulae enunciated by Ramanujan,” Proc. London Math. Soc. 21, 235-255 (1923), especially Eqs. (R.3) and (R.22).

    Google Scholar 

  36. H. Iwaniec, Introduction to the Spectral Theory of Automorphic Forms (Revista Matemática Iberoamericana, Madrid, 1995), pp. 193-194.

    Google Scholar 

  37. P. Sarnak, personal communication, 2000.

  38. P. Sarnak, “Integrals of products of eigenfunctions,” International Math. Res. Notices, 251-260 (1994).

  39. T. C. Watson, Ph.D. thesis, Princeton University, 2000.

  40. R. A. Rankin, Modular forms and functions (Cambridge University Press, 1977).

  41. Z. Rudnick and P. Sarnak, “The behaviour of eigenstates of arithmetic hyperbolic manifolds,”Comm. Math. Phys. 161, 195-213 (1994).

    Google Scholar 

  42. G. Steil, “Eigenvalues of the Laplacian for Bianchi groups,” in Emerging Applications of Number Theory, D. Hejhal, J. Friedman, M. Gutzwiller, and A. Odlyzko, eds. (IMA, Vol. 109) (Springer, 1999), pp. 617-641.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Uppsala University, Box 480, S-75106, Uppsala, Sweden

    Dennis A. Hejhal & Andreas Strömbergsson

  2. School of Mathematics, University of Minnesota, Minneapolis, Minnesota, 55455

    Dennis A. Hejhal

Authors
  1. Dennis A. Hejhal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andreas Strömbergsson
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hejhal, D.A., Strömbergsson, A. On Quantum Chaos and Maass Waveforms of CM-Type. Foundations of Physics 31, 519–533 (2001). https://doi.org/10.1023/A:1017521729782

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1017521729782

Keywords

Search

Navigation