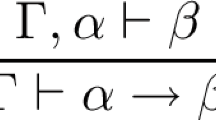Abstract
We show that in quantum logic of closed subspaces of Hilbert space one cannot substitute quantum operations for classical (standard Hilbert space) ones and treat them as primitive operations. We consider two possible ways of such a substitution and arrive at operation algebras that are not lattices what proves the claim. We devise algorithms and programs which write down any two-variable expression in an orthomodular lattice by means of classical and quantum operations in an identical form. Our results show that lattice structure and classical operations uniquely determine quantum logic underlying Hilbert space. As a consequence of our result, recent proposals for a deduction theorem with quantum operations in an orthomodular lattice as well as a, substitution of quantum operations for the usual standard Hilbert space ones in quantum logic prove to be misleading. Quantum computer quantum logic is also discussed.
Similar content being viewed by others
REFERENCES
B. Christianson, P. L. Knight, and T. Beth, Implementations of quantum logic, Philos. Trans. Roy. Soc. London Ser. A 356(1743), 1823–1838 (1998).
G. W. Mackey, The Mathematical Foundations of Quantum Mechanics (Benjamin, New York, 1963).
V. S. Varadarajan, Geometry of Quantum Theory, Vols. 1 and 2 (Wiley, New York, 1968/1970).
H. A. Keller, Ein nicht-klassischer Hilbertscher Raum, Math. Z. 172, 41–49 (1980).
B. M. Boghosian and W. Taylor, Simulating quantum mechanics on a quantum computer, Phys. D 120, 30–42 (1998); http://xxx.lanl.gov/abs/quant-ph/9701019.
R. Godowski, Varieties of orthomodular lattices with a strongly full set of state, Demonstratio Math. 14, 725–733 (1981).
R. Godowski and R. Greechie, Some equations related to the states on orthomodular lattices, Demonstratio Math. 17, 241–250 (1984).
R. Mayet, Equational bases for some varieties of orthomodular lattices related to states, Algebra Universalis 23, 167–195 (1986).
N. D. Megill and M. Pavičić, Equations, states, and lattices of infinite-dimensional Hilbert space, Internat. J. Theoret. Phys. 39, 2349–2391 (2000); http://xxx.lanl.gov/ abs/quant-ph/0009038.
M. L. Dalla Chiara, Quantum logic, in Hand-book of Philosophical Logic, Vol. III, D. Gabbay and F. Guentliner, eds. (Reidel, Dordrecht, 1986), pp. 427–469.
M. L. Dalla Chiara and R. Giuntini, Quantum logic, http://xxx.lanl.gov/abs/quant-ph/ 0101028 (2001).
P. F. Gibbins, Particles and Paradoxes: The Limits of Quantum Logics (Cambridge University Press, Cambridge, 1987).
M. Jammer, The Philosophy of Quantum Mechanics. The Interpretations of Quantum Mechanics in Historical Perspective (Wiley, New York, 1974).
G. Kalmbach, Orthomodular Lattices (Academic, London, 1983).
P. Mittelstaedt, Quantum Logic (Synthese Library, Vol. 18) (Reidel, London, 1978).
C. Piron, Foundations of Quantum Physics (Benjamin, Reading, Massachusetts, 1976).
G. T. Rüttimann, Logikkalku´le der Quantenphysik. Eine Abhandlung zur Ermittlung der formal-logischen Systeme, die der nicht-relativistischen Quantentheorie zugrundeliegen (Duncker &;; Humblot, Berlin, 1977).
M. Pavičić and N. D. Megill, “Non-orthomodular models for both standard quantum logic and standard classical logic: Repercussions for quantum computers,” Helv. Phys. Acta 72, 189–210 (1999); http://xxx.lanl.gov/abs/quart-ph/9906101.
N. D. Megill and M. Pavičić, “Orthomodular lattices and a quantum algebra,” Internat. J. Theoret. Phys. 40, 1387–1410 (2001); http://xxx.lanl.gov/abs/quant-ph/0103135.
P. D. Finch, Quantum logic as an implication algebra, Bull. Austral. Math. Soc. 2, 101–106 (1970).
L. Román and B. Rumbos, Quantum logic revisited, Found. Phys. 21, 793–734 (1991).
L. Román and R. E. Zuazua, Quantum implication, Internat. J. Theoret. Phys. 38, 793–797 (1999).
J. Malinowski, The deduction theorem for quantum logic—some negative results, J. Symbolic Logic 55, 615–625, 1990.
B. D'Hooghe and J. Pykacz, On some new operations on orthomodular lattices, Internat. J. Theoret. Phys. 39, 641–652 (2000).
H. Dishkant, The first-order predicate calculus based on the minimal logic of quantum mechanics, Rep. Math. Logic 3, 9–18 (1974).
G. N. Georgacarakos, Equationally definable implication algebras for orthomodular lattice, Stud. Logica 39, 5–18 (1980).
G. M. Hardegree, Material implication in orthomodular (and Boolean) lattice, Notre Dame J. Formal Logic 22, 163–182 (1981).
M. Pavičić and N. D. Megill, Quantum and classical implication algebras with primitive implications, Internat. J. Theoret. Phys. 37, 2091–2098 (1998).
L. Beran, Orthomodular Lattices; Algebraic Approach (Reidel, Dordrecht, 1985).
M. Pavičić, Minimal quantum logic with merged implications, Internat. J. Theoret. Phys. 26, 845–852 (1987).
R. I. Goldblatt, Semantic analysis of orthologic, J. Philos. Logic 3, 19–35 (1974).
M. Navara, On generating finite orthomodular sublattices, Tatra Mt. Math. Publ. 10, 109–117 (1997).
J. C. Abbott, Orthoimplication algebra, Stud. Logica, 35, 173–177 (1976).
B. D. McKay, N. D. Megill, and M. Pavičić, Algorithms for Greechie diagrams, Internat. J. Theoret. Phys. 39, 2393–2417 (2000); httl)://xxx.lanl.gov/abs/quant-ph/0009039.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Megill, N.D., Pavičić, M. Deduction, Ordering, and Operations in Quantum Logic. Foundations of Physics 32, 357–378 (2002). https://doi.org/10.1023/A:1014857228326
Issue Date:
DOI: https://doi.org/10.1023/A:1014857228326