Abstract
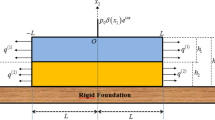
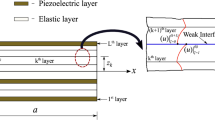
In this paper, we consider the dynamic response of a pre-stressed sandwich plate-strip with a piezoelectric core and elastic layers under the action of a time-harmonic force resting on a rigid foundation. The investigation is carried out within the framework of the piecewise homogeneous body model by utilizing the exact equations of motion and relations of the linear theory of electro-elasticity. It is assumed that there is a shear-spring-type imperfect contact between the layers, but a complete contact between the plate-strip and the rigid foundation. A mathematical model of the problem is constructed, and the governing equations of motion are solved by employing the finite element method (FEM). Numerical results illustrating the influence of a change in the value of the shear-spring parameter on the dynamic response of the plate-strip are then presented.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A.N. Guz, Elastic Waves in a Body with Initial (Residual) Stresses, A.C.K., 2004 (in Russian).
A. Cilli, A. Ozturk, Dispersion of torsional waves in initially stressed multilayered circular cylinders, Mech. Compos. Mater. 46 (2) (2010) 227–236.
A.D. Zamanov, E.R. Agasiyev, Dispersion of Lamb waves in a three-layer plate made from compressible with finite deformations, Mech. Compos. Mater. 46 (6) (2011) 583–592.
H. Wen-tao, X. Tang-dai, C. Wei-yun, Influence of lateral initial pressure on axisymmetric wave propagation in hollow cylinder based on first power hypo-elastic model, J. Central South Univ. 21 (2) (2014) 753–760.
A. Daşdemir, M. Eröz, Mathematical modeling of dynamical stress field problem for a pre-stressed bi-layered plate-strip, Bull. Malaysian Math. Sci. Soc. 38 (2) (2015) 733–760.
J. Liu, Y. Wang, B. Wang, Propagation of shear horizontal surface waves in a layered piezoelectric half-space with an imperfect interface, IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57 (8) (2010) 1875–1879.
J.R. Berger, P.A. Martin, S.J. McCaffery, Time-harmonic torsional waves in a composite cylinder with an imperfect interface, J. Acoust. Soc. Am. 107 (3) (2000) 1161–1167.
M.X. Deng, Analysis of second-harmonic generation of Lamb waves propagating in layered planar structures with imperfect interfaces, Appl. Phys. Lett. 88 (22) (2006) 221902.
S.D. Akbarov, C. Ipek, Dispersion of axisymmetric longitudinal waves in a pre-strained imperfectly bonded bi-layered hollow cylinder, Comput. Mater. Continua 30 (2) (2012) 99–14.
T. Kepceler, Torsional wave dispersion relations in a pre-stressed bi-material compounded cylinder with an imperfect interface, Appl. Math. Modell. 34 (12) (2010) 4058–4073.
Y. Pang, J. Liu, Reflection and transmission of plane waves at an imperfectly bonded interface between piezoelectric and piezomagnetic media, Eur. J. Mech. A Solids 30 (5) (2011) 731–740.
J. Yang, An Introduction to the Theory of Piezoelectricity, Springer, 2005.
S.I. Rokhlin, J. Wang, Analysis of boundary conditions for elastic wave interaction with an interface between two solids, J. Acoust. Soc. Am. 89 (2) (1991) 503–515.
J.P. Jones, J.S. Whittier, Waves at a flexibly bonded interface, J. Appl. Mech. 34 (4) (1967) 905–909.
O.C. Zienkiewicz, R.L. Taylor, The Finite Element Method, Basic Formulation and Linear Problems, McGraw-Hill, 1989.
Y.S. Uflyand, Integral Transformations in the Theory of Elasticity, Nauka, 1963 (in Russian).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Daşdemir, A. Effect of imperfect bonding on the dynamic response of a pre-stressed sandwich plate-strip with elastic layers and a piezoelectric core. Acta Mech. Solida Sin. 30, 658–667 (2017). https://doi.org/10.1016/j.camss.2017.10.005
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1016/j.camss.2017.10.005