Abstract
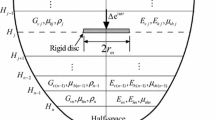
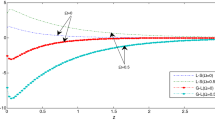
A cylindrical system of vector functions, the stiffness matrix method and the corresponding recursive algorithm are proposed to investigate the static response of transversely isotropic, layered magneto-electro-elastic (MEE) structures over a homogeneous half-space substrate subjected to circular surface loading. In terms of the system of vector functions, we expand the extended displacements and stresses, and deduce two sets of ordinary differential equations, which are related to the expansion coefficients. The solution to one of the two sets of these ordinary differential equations can be evaluated by using the stiffness matrix method and the corresponding recursive algorithm. These expansion coefficients are then integrated by adaptive Gaussian quadrature to obtain the displacements and stresses in the physical domain. Two types of surface loads, mechanical pressure and electric loading, are considered in the numerical examples. The calculated results show that the proposed technique is stable and effective in analyzing the layered half-space MEE structures under surface loading.
Similar content being viewed by others
References
S.J. Singh, Static deformation of a transversely isotropic multilayered half-space by surface loads, Phys. Earth Planet. Inter. 42 (1986) 263–273.
K. Wang, Analysis and calculation of stresses and displacements in layered elastic systems, Acta Mech. Sin. 3 (1987) 251–260.
E. Pan, M. Bevis, F. Han, et al., Surface deformation due to loading of a layered elastic half-space: a rapid numerical kernel based on a circular loading element, Geophys. J. Int. 171 (2007) 11–24.
C.W. Nan, M.I. Bichurin, S.X. Dong, et al., Multiferroic magnetoelectric composites: historical perspective, status, and future directions, J. Appl. Phys. 103 (2008) 031101.
A.A. Semenov, S.F. Karmanenko, B.A. Kalinikos, et al., Dual-tunable hybrid wave ferrite-ferroelectric microwave resonator, Electron. Lett. 42 (2006) 641–642.
H.M. Wang, E. Pan, A. Sangghaleh, et al., Circular loadings on the surface of an anisotropic and magnetoelectroelastic half-space, Smart Mater. Struct. 21 (2012) 075003–075014.
H.J. Chu, Y. Zhang, E. Pan, et al., Circular surface loading on a layered multiferroic half-space, Smart Mater. Struct. 20 (2011) 035020.
J. Ma, LL. Ke, Y.S. Wang, Frictionless contact of a functionally graded magneto-electro-elastic layered half-plane under a conducting punch, Int. J. Solids Struct. 51 (2014) 2791–2806.
J. Ma, L.L. Ke, Y.S. Wang, Sliding frictional contact of functionally graded magneto- electro-elastic materials under a conducting flat punch, J. Appl. Mech. 82 (2015) 011009.
J. Ma, S. EI-Borgi, L.L. Ke, et al., Frictional contact problem between a functionally graded magneto-electro-elastic layer and a rigid conducting flat punch with frictional heat generation, J. Thermal Stress. 39 (2016) 245–277.
E. Pan, Static Green’s functions in multilayered half-spaces, Appl. Math. Model. 21 (1997) 509–521.
J.Y. Chen, E. Pan, P.R. Heyliger, Static deformation of a spherically anisotropic and multilayered magneto-electro-elastic hollow sphere, Int. J. Solids Struct. 60–61 (2015) 66–74.
E. Pan, J.Y. Chen, M. Bevis, et al., An analytical solution for the elastic response to surface loads imposed on a layered, transversely isotropic and self-gravitating Earth, Geophys. J. Int. 203 (2015) 2150–2181.
L. Wang, I. Rokhlin S, Stable reformulation of transfer matrix method for wave propagation in layered anisotropic media, Ultrasonics 39 (2001) 413–424.
S.I. Rokhlin, L. Wang, Stable recursive algorithm for elastic wave propagation in layered anisotropic media: stiffness matrix method, J. Acoust. Soc. Am. 112 (2002) 822–834.
J.T. Ratnanather, J.H. Kim, S.R. Zhang, et al., Algorithm 935: IIPBF, a MATLAB toolbox for infinite integral of products of two Bessel functions, ACM Trans. Math. Softw. 40 (2014) 131–162.
E. Pan, Exact solution for simply supported and multilayered magneto-electro-elastic plates, J. Appl. Mech. 68 (2001) 608–618.
F. Ramirez, P.R. Heyliger, E. Pan, Free vibration response of two-dimensional magneto-electro-elastic laminated plates, J. Sound Vib. 292 (2006) 626–644.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chen, J., Guo, J. Static response of a layered magneto-electro-elastic half-space structure under circular surface loading. Acta Mech. Solida Sin. 30, 145–153 (2017). https://doi.org/10.1016/j.camss.2017.03.003
Published:
Issue Date:
DOI: https://doi.org/10.1016/j.camss.2017.03.003