Skip to main content
SpringerLink
Log in

Homotopy Perturbation Solution and Periodicity Analysis of Nonlinear Vibration of Thin Rectangular Functionally Graded Plates

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

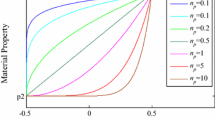
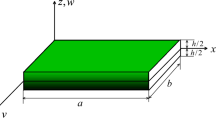
In this paper nonlinear analysis of a thin rectangular functionally graded plate is formulated in terms of von-Karman’s dynamic equations. Functionally Graded Material (FGM) properties vary through the constant thickness of the plate at ambient temperature. By expansion of the solution as a series of mode functions, we reduce the governing equations of motion to a Duffing’s equation. The homotopy perturbation solution of generated Duffing’s equation is also obtained and compared with numerical solutions. The sufficient conditions for the existence of periodic oscillatory behavior of the plate are established by using Green’s function and Schauder’s fixed point theorem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Yang, J. and Shen, H.S., Dynamic response of initially stressed functionally graded rectangular thin plates. Composite Structures, 2001, 54: 497–508.

    Article  Google Scholar 

  2. Shahrjerdi, A., Mustapha, F., Bayat, M. and Majid, D.L.A., Free vibration analysis of solar functionally graded plates with temperature-dependent material properties using second order shear deformation theory. Journal of Mechanical Science and Technology, 2011, 25(9): 2195–2209.

    Article  Google Scholar 

  3. Reddy, J.N. and Cheng, Z.Q., Frequency of functionally graded plates with three-dimensional asymptotic approach. Journal of Engineering Mechanics, 2003, 129: 896–900.

    Article  Google Scholar 

  4. Hao, Y.X., Zhang, W., Yang, J. and Li, S.Y., Nonlinear dynamic response of a simply supported rectangular functionally graded material plate under the time-dependent thermal mechanical loads. Journal of Mechanical Science and Technology, 2011, 25(7): 1637–1646.

    Article  Google Scholar 

  5. Nayfeh, A.H. and Mook, D.T., Nonlinear Oscillations. New York: Wiley, 1979.

    MATH  Google Scholar 

  6. Esmailzadeh, E. and Nakhaie-Jazar, G., Periodic behavior of a cantilever beam with end mass subjected to harmonic base excitation. International Journal of Non-Linear Mechanics, 1998, 33: 567–577.

    Article  Google Scholar 

  7. Cronin, J., Fixed Points and Topological Degree in Nonlinear Analysis, Math Survey II. American Mathematical Society, Providence, RI, 1964.

  8. Praveen, G.N. and Reddy, J.N., Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates. International Journal of Solids and Structures, 1998, 35: 4457–4476.

    Article  Google Scholar 

  9. Gao, L., Wang, J., Zhong, Z. and Du, J., An analysis of surface acoustic wave propagation in functionally graded plates with homotopy analysis method. Acta Mechanica, 2009, 208: 249–258.

    Article  Google Scholar 

  10. Gao, L., Wang, J., Zhong, Z. and DU, J., An analysis of surface acoustic wave propagation in a plate of functionally graded materials with a layered model. Science China Physics, Mechanics and Astronomy, 2008, 51: 165–175.

    Article  Google Scholar 

  11. Gao, L., Wang, J., Zhong, Z. and DU, J., An exact analysis of surface acoustic waves in a plate of functionally graded materials. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2009, 56: 2693–2700.

    Article  Google Scholar 

  12. Wang, J., Yang, J. and Li, J., Energy trapping of thickness-shear vibration modes of elastic plates with functionally graded materials. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2007, 54: 687–690.

    Article  Google Scholar 

  13. Yang, J. and Shen, H.S., Vibration characteristics and transient response of shear-deformable functionally graded plates in thermal environments. Journal of Sound and Vibration, 2002, 255: 579–602.

    Article  Google Scholar 

  14. Woo, J. and Meguid, S.A., Nonlinear analysis of functionally graded plates and shallow shells. International Journal of Solids and Structures, 2001, 38: 7409–7421.

    Article  Google Scholar 

  15. Chen, C.S., Nonlinear vibration of a shear deformable functionally graded plate. Composite Structures, 2005, 68: 295–302.

    Article  Google Scholar 

  16. Allahverdizadeh, A., Naei, M.H. and Nikkhah Bahrami, M., Nonlinear free and forced vibration analysis of thin circular functionally graded plates. Journal of Sound and Vibration, 2008, 310: 966–984.

    Article  Google Scholar 

  17. Mehri, B. and Hamedani, G.G., On the existence of periodic solutions of nonlinear second order differential equations. SIAM Journal on Applied Mathematics, 1975, 29: 72–76.

    Article  MathSciNet  Google Scholar 

  18. Esmailzadeh, E. and Jalili, N., The parametric response of cantilever Timoshenko beams with tip mass under harmonic support motion. International Journal of Non-Linear Mechanics, 1998, 33: 765–781.

    Article  MathSciNet  Google Scholar 

  19. Feiz-Dizaji, A., Salimpour, M.R. and Jam, F., Flow field of a third-grade non-Newtonian fluid in the annulus of rotating concentric cylinders in the presence of magnetic field. Journal of Mathematical Analysis and Applications, 2008, 337: 632–645.

    Article  MathSciNet  Google Scholar 

  20. Shadnam, M., Rahimzadeh Rofooei, F., Mofid, M. and Mehri, B., Periodicity in the response of nonlinear plate under moving mass. Thin-Walled Structures, 2002, 40: 238–295.

    Article  Google Scholar 

  21. Timoshenko, S. and Woinowsky-Krieger, S., Theory of Plates and Shells, second ed. New York: McGraw-Hill, 1959.

    MATH  Google Scholar 

  22. Touloukian, Y.S., Thermo Physical Properties of High Temperature Solid Materials. New York: Macmillan, 1967.

    Google Scholar 

  23. Shafiee, H., Naei, M.H. and Eslami, M.R., In-plane and out-of-plane buckling of arches made of FGM. International Journal of Mechanical Sciences, 2006, 48: 907–915.

    Article  Google Scholar 

  24. Reddy, J.N. and Chin, C.D., Thermo-mechanical analysis of functionally graded cylinders and plates. Journal of Thermal Stresses, 1998, 21: 593–626.

    Article  Google Scholar 

  25. Brush, D.O. and Almroth, B.O., Buckling of Bars, Plates and Shells. New York: McGraw- Hill, 1975.

    MATH  Google Scholar 

  26. Amabili, M., Nonlinear Vibrations and Stability of Shells and Plates. New York: Cambridge University, 2008.

    Book  Google Scholar 

  27. He, J.H., Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering, 1999, 178: 257–262.

    Article  MathSciNet  Google Scholar 

  28. Nayfeh, A.H., Introduction to Perturbation Techniques. New York: Wiley, 1993.

    MATH  Google Scholar 

  29. Griffle, D.H., Applied Functional Analysis. New York: Wiley, 1985.

    Google Scholar 

  30. Dizaji, A.F., Sepiani, H.A. and Ebrahimi, F., Allahverdizadeh, A. and Sepiani, H.A., Schauder fixed point theorem based existence of periodic solution for the response of Duffing’s oscillator. Journal of Mechanical Science and Technology, 2009, 23: 2299–2307.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Engineering - Emerging Technologies, University of Tabriz, Tabriz, Iran

    A. Allahverdizadeh

  2. School of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran

    A. Allahverdizadeh, R. Oftadeh, M. J. Mahjoob & M. H. Naei

  3. Department of Mechanical and Industrial Engineering, Northeastern University, Boston, MA, United States

    R. Oftadeh

Authors
  1. A. Allahverdizadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Oftadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. J. Mahjoob
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. H. Naei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Allahverdizadeh.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Allahverdizadeh, A., Oftadeh, R., Mahjoob, M.J. et al. Homotopy Perturbation Solution and Periodicity Analysis of Nonlinear Vibration of Thin Rectangular Functionally Graded Plates. Acta Mech. Solida Sin. 27, 210–220 (2014). https://doi.org/10.1016/S0894-9166(14)60031-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S0894-9166(14)60031-8

Key Words

Search

Navigation