Abstract
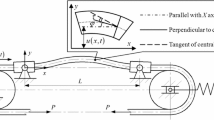
This paper presents an analysis on the nonlinear dynamics and multi-pulse chaotic motions of a simply-supported symmetric cross-ply composite laminated rectangular thin plate with the parametric and forcing excitations. Firstly, based on the Reddy’s third-order shear deformation plate theory and the model of the von Karman type geometric nonlinearity, the nonlinear governing partial differential equations of motion for the composite laminated rectangular thin plate are derived by using the Hamilton’s principle. Then, using the second-order Galerkin discretization, the partial differential governing equations of motion are transformed to nonlinear ordinary differential equations. The case of the primary parametric resonance and 1:1 internal resonance is considered. Four-dimensional averaged equation is obtained by using the method of multiple scales. From the averaged equation obtained here, the theory of normal form is used to give the explicit expressions of normal form. Based on normal form, the energy phase method is utilized to analyze the global bifurcations and multi-pulse chaotic dynamics of the composite laminated rectangular thin plate. The theoretic results obtained above illustrate the existence of the chaos for the Smale horseshoe sense in a parametrical and forcing excited composite laminated thin plate. The chaotic motions of the composite laminated rectangular thin plate are also found by using numerical simulation, which also indicate that there exist different shapes of the multi-pulse chaotic motions for the composite laminated rectangular thin plate.
Similar content being viewed by others
References
Abe, A., Kobayashi, Y. and Yamada, G., Two-mode response of simply supported, rectangular laminated plate. International Journal of Non-linear Mechanics, 1998, 33: 675–690.
Bhimaraddi, A., Large amplitude vibrations of imperfect antisymmetric angle-ply laminated plates. Journal of Sound and Vibration, 1999, 162: 457–470.
Ye, M., Sun, Y., Zhang, W., Zhan, X.P. and Ding, Q., Nonlinear oscillations and chaotic dynamics of an antisymmetric cross-ply composite laminated rectangular thin plate under parametric excitation. Journal of Sound and Vibration, 2005, 287: 723–758.
Ribeiro, P. and Duarte, R.P., From periodic to chaotic oscillations in composite laminated plates. Computers and Structures, 2006, 84: 1629–1639.
Zhang, W., Song, C.Z. and Ye, M., Further studies on nonlinear oscillations and chaos of a rectangular symmetric cross-by laminated plate under parametric excitation. International Journal of Bifurcation and Chaos, 2006, 16: 325–347.
Abe, A., Kobayashi, Y. and Yamada, G., Nonlinear dynamic behaviors of clamped laminated shallow shells with one-to-one internal resonance. Journal of Sound and Vibration, 2007, 304: 957–968.
Chen, C.S., Fung, C.P. and Chien, R.D., Nonlinear vibration of an initially stressed laminated plate according to a higher-order theory. Composite Structures, 2007, 77: 521–532.
Kazancl, Z. and Mecitog, Z., Nonlinear dynamic behavior of simply supported laminated composite plates subjected to blast load. Journal of Sound and Vibration, 2008, 317: 883–897.
Achchhe, L., Singh, B.N. and Kumar, R., Effect of random system properties on the initial buckling of laminated composite plate resting on an elastic foundation. International Journal of Structural Stability and Dynamics, 2008, 8: 1–28.
Hao, Y.X., Chen, L.H., Zhang, W. and Lei, J.G., Nonlinear oscillations, bifurcations and chaos of functionally graded materials plate. Journal of Sound and Vibration, 2008, 312: 862–892.
Zhang, W., Yang, J. and Hao, Y.X., Chaotic vibrations of an orthotropic FGM rectangular plate based on third-order shear deformation theory. Nonlinear Dynamics, 2010, 59: 619–660.
Zhang, W., Guo, X.Y. and Lai, S.K., Research on periodic and chaotic oscillations of composite laminated plates with one-to-one internal resonance. International Journal of Nonlinear Sciences and Numerical Simulation, 2009, 10: 1567–1583.
Chandrashekhar, M. and Ranjan Ganguli, Nonlinear vibration analysis of composite laminated and sandwich plates with random material properties. International Journal of Mechanical Sciences, 2010, 52: 874–891.
Zhang, W., Global and chaotic dynamics for a parametrically excited thin plate. Journal of Sound and Vibration, 2001, 239: 1013–1036.
Shadnam, M.R., Rofooei, F.R., Mofid, M. and Mehri, B., Periodicity in the response of nonlinear plate under moving mass. Thin-walled Structures, 2002, 40: 283–295.
Wang, N.Q. and Qin, L.Q., The design and analysis of vibration structure of vertical dynamic balancing machine. Acta Mechanica Solida Sinica, 2005, 26(3): 172–182 (in Chinese).
Wang, N.Q. and Qin, L.Q., Chaotic transients in a curved fluid conveying tube. Acta Mechanica Solida Sinica, 2005, 26(3): 207–214 (in Chinese).
Awrejcewicz, J., Krysko, V.A. and Narkaitis, G.G., Bifurcations of a thin plate-strip excited transversally and axially. Nonlinear Dynamics, 2003, 32: 187–209.
Yeh, Y.L., Chaotic and bifurcation dynamic behavior of a simply supported rectangular orthotropic plate with thermo-mechanical coupling. Chaos, Solitons & Fractals, 2005, 24: 1243–1255.
Ding, H. and Chen, L.Q., Nonlinear dynamics of axially accelerating viscoelastic beams based on differential quadrature. Acta Mechanica Solida Sinica, 2009, 22(3): 267–275.
Haller, G. and Wiggins, S., Orbits homoclinic to resonance: the Hamiltonian. Physica D, 1993, 66: 298–346.
Haller, G. and Wiggins, S., Multi-pulse jumping orbits and homoclinic trees in a modal truncation of the damped-forced nonlinear Schrodinger equation. Physica D, 1995, 85: 311–347.
Haller, G. and Wiggins, S., Geometry and chaos near resonant equilibria of 3-DOF Hamiltonian systems. Physica D, 1996, 90: 319–365.
Haller, G., Chaos Near Resonance. New York: Springer-Verlag, 1999.
Malhotra, N., Namachchivaya, N.S. and McDonald, R.J., Multipulse orbits in the motion of flexible spinning discs. Journal of Nonlinear Science, 2002, 12: 1–26.
Yao, M.H. and Zhang, W., Multi-Pulse Shilnikov orbits and chaotic dynamics in nonlinear nonplanar motion of a cantilever beam. International Journal of Bifurcation and Chaos, 2005, 15: 3923–3952.
Zhang, W. and Yao, M.H., Multi-pulse orbits and chaotic dynamics in motion of parametrically excited viscoelastic moving belt. Chaos, Solitons and Fractals, 2006, 28: 42–66.
Yao, M.H. and Zhang, W., Multi-pulse Shilnikov orbits and chaotic dynamics of a parametrically and externally excited thin plate. International Journal of Bifurcations and Chaos, 2007, 17: 1–25.
Zhang, J.H., Zhang, W., Yao, M.H. and Guo, X.Y., Multi-pulse Shilnikov chaotic dynamics for a non-autonomous buckled thin plate under parametric excitation. International Journal of Nonlinear Sciences and Numerical Simulation, 2008, 9: 381–394.
Li, S.B., Zhang, W. and Hao, Y.X., Multi-pulse chaotic dynamics of a functionally graded material rectangular plate with one-to-one internal resonance. International Journal of Nonlinear Sciences and Numerical Simulation, 2010, 11:351–362.
Zhang, W., Zhang, J.H. and Yao, M.H., The extended Melnikov method for non-autonomous nonlinear dynamical systems and application to multi-pulse chaotic dynamics of a buckled thin plate. Nonlinear Analysis: Real World Applications, 2010, 11: 1442–1457.
Reddy, J.N., Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. New York: CRC Press, 2004.
Jones, R.M., Mechanics of Composite Materials, second ed. New York: McGraw-Hill, 1997.
Nayfeh, A.H. and Mook, D.T., Nonlinear Oscillations. New York: Wiley-Interscience, 1979.
Yu, P., Zhang, W. and Bi, Q.S., Vibration analysis on a thin plate with the aid of computation of normal forms. International Journal of Non-Linear Mechanics, 2001, 36: 597–627.
Parker, T.S. and Chua, L.O., Practical Numerical Algorithms for Chaotic Systems. New York: Springer-Verlag, 1989.
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (Nos. 10732020 and 11072008), the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHRIHLB).
Rights and permissions
About this article
Cite this article
Guo, X., Zhang, W. & Yao, M. Multi-Pulse Orbits and Chaotic Dynamics of a Composite Laminated Rectangular Plate. Acta Mech. Solida Sin. 24, 383–398 (2011). https://doi.org/10.1016/S0894-9166(11)60039-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1016/S0894-9166(11)60039-6