Vector mesons in medium

Abstract

After decades-long attempts to measure the mass shift and understand the origin of hadron mass, it became clear that one has to analyze hadrons with small vacuum width. Also, to identify the effect of chiral symmetry breaking, one has to start by looking at chiral partners. Such considerations inevitably points to studying K^∗ and K₁ in matter. The masses of both particles can potentially be measured from nuclear target based experiments and/or heavy ion collisions. Once the masses and mass difference of K^∗ and K₁ mesons are measured, we will be closer to understanding the origin of hadron mass and the effects of chiral symmetry breaking. We will review the topic using the operator product expansion (OPE) perspective.

1 Introduction

Traditionally, the mass of a composite particle can be expressed in terms of the masses of its constituents and a small binding energy. This picture does not hold for the mass of a hadron. This is because the origin of a hadron mass is intricately related to the low energy property of QCD, such as confinement and chiral symmetry breaking effects, which are analytically still not completely understood. It is known that chiral symmetry breaking is partly responsible for the generation of mass [1–5]. Therefore, if one can identify the effect of chiral symmetry breaking on the masses of hadrons, we will be able to build models and then a theory to understand the origin of the masses of hadrons.

In the original in-medium QCD sum rules [4], the changes of the vector meson masses were dominantly due to the change of the 4-quark condensate for the light quark system and the strange quark condensate for the strange quark system. Experiments have since then been performed worldwide to observe mass shift of hadrons at finite temperature or density [6, 7].

Experimental as well as theoretical efforts so far have led us to the following conclusions [8]. (1) Dilepton spectra do not suffer from strong final state interaction with the medium when the signal emanates from inside the nucleus but has many sources and is low in the yield. (2) Nuclear target experiments have the advantage that the target density remains constant and that even at nuclear matter density, the order parameter is known to decease by almost 30%. (3) While reactions involving hadronic decays have final state interaction effects, the problem can be overcome by focusing on mesons with small width in the vacuum and then combining the measurement of excitation functions and the transparency ratios [9]. (4) The individual meson mass could behave differently depending on whether the hadron is in nuclear matter or at finite temperature, but the mass difference between chiral partners will only depend on the chiral order parameter and should be universal [10]. Therefore, it is important to measure the mass shift of chiral partners simultaneously to establish the basis for mass shift and chiral symmetry restoration and then look at the individual masses.

There is a universal feature that is affected by chiral symmetry breaking. In fact, the question of whether chiral symmetry breaking is the origin of the hadron mass can be answered by isolating the chiral symmetry breaking effects in the vacuum. In the past, similar question has been addressed in lattice gauge theory, where the hadronic correlation functions have been studied after the short distance Coulomb and confinement physics have been eliminated through the lattice cooling process [11]. As we will see, using operator product expansion (OPE), one can also isolate chiral symmetry breaking effects. Studying the chiral partners will therefore be the universal starting point to understand the effects of chiral symmetry breaking on the mass of a hadron. In particular, measuring them in nuclear matter or finite temperature will enable us to confirm the relation between chiral symmetry breaking and hadron mass experimentally.

Such considerations inevitably lead us to consider the K₁ and K^∗ in medium [1, 8]. In the vacuum, the low-lying modes that couple to the vector current are the K^∗(892) and K^∗(1410) while for the axial vector current they are the K₁(1270) and K₁(1400). If chiral symmetry is partially restored, the spectral density will tend to become degenerate so that the lowest distinctive poles in the respective currents will approach each other. Therefore, in a recent work [1], we investigated the spectral modification of open strange meson K₁ through the axial-vector current in nuclear matter using QCD sum rules.

Measuring the open strange meson in the vector channel, namely the K^∗+ through the decay K^∗+→K⁺+γ was suggested in Ref. [12] as a promising signal in the measurement of the spectral change of a vector meson. Both the K₁(1270) and the K^∗(892) have widths smaller than their non-strange counter parts, namely 90 MeV and 47 MeV, respectively, compared to more than 250 MeV and 150 MeV for the a₁ and the ρ. At the same time, they are also chiral partners so that their mass difference is sensitive to the chiral order parameter.

We note that $K_{1}^{+}$ and $K_{1}^{-}$ become non-degenerate in the nuclear medium due to the presence of nucleons which break charge conjugation invariance in the medium. This is not a problem as long as we compare K^∗ and K¹ with the same charge states as they remain chiral partners.

In this review, we will discuss how to identify the effects of chiral symmetry breaking at the operators level. In Section 2, we discuss the chiral order parameters and their effects on correlation functions. In Section 3, we will discuss how the U _A(1) symmetry breaking effect contributes in the correlation functions. Section 4 discusses the K^∗ and K₁. Phenomenological considerations are given in Section 5. Conclusions are given in Section 6.

2 Chiral order parameter

Let us first discuss the importance of condensate in discussing the hadron masses. We are still far from understanding the low energy physics directly from QCD variables. Yet, important physical effects can be summarized in terms of local operators. The most important operators are chiral order parameters: that is operators that characterizes the breaking of chiral symmetry. The commonly known chiral order parameter can be rewritten in several forms.

$$\begin{array}{@{}rcl@{}} \langle \bar{q} q \rangle & \equiv & {\lim}_{x \rightarrow 0} - \langle \text{Tr} [ S(0,x) ] ] \rangle \\ & = & {\lim}_{x \rightarrow 0} - \frac{1}{2} \langle \text{Tr} [ S(0,x)- i\gamma_{5} S(0,x) i \gamma_{5} ] ] \rangle \\ & = & -\pi \langle \rho(\lambda=0) \rangle. \end{array} $$

(1)

The gauge invariant part of the combination of propagators (S(x,y)−iγ⁵S(x,y)iγ⁵) can be identified as a convenient expression of a chiral order parameter. The third line, due to Banks-Casher [13], shows the density of zero eigenvalue in the Euclidean formalism. The formula is useful for identifying the origin of chiral symmetry breaking in terms of quark eigenvalues that can be usefully implemented in lattice gauge theory calculations.

Using Eq. (1) one can identify many more order parameters for chiral symmetry breaking. A set of order parameters can be obtained by looking at the difference in the correlation functions of chiral partners. For example, the difference between the scalar and pseudo scalar correlation functions is an order parameter [14].

$$\begin{array}{@{}rcl@{}} \Delta_{S-P} (q)\!\! & = & \int d^{4}x e^{iqx} \left\langle \mathcal{T} \left(\bar{q} \tau^{a} q(x) \bar{q} \tau^{a} q(0)\right.\right.\\&&-\left.\left. \bar{q} \tau^{a} i\gamma^{5} q(x) \bar{q} \tau^{a} i\gamma^{5} q(0) \right) \right\rangle \\ \!\!& = & \int d^{4}x e^{iqx} \frac{1}{2} \left\langle \text{Tr} \left[ \tau^{a} \tau^{a} \left(i \gamma^{5} S(x,0) i \gamma^{5} -S(x,0) \right)\right.\right.\\ &&\left.\left.\left(S(0,x)- i \gamma^{5} S(0,x) i \gamma^{5} \right) \right] \right\rangle. \end{array} $$

(2)

As can be seen above, the combination of propagators appear, which will be proportional to the density of zero modes. Using these methods, one can construct chiral order parameters of different types of correlation functions. We have added the flavor matrix in the scalar current. In principle, this is not necessary because the additional disconnected diagram in the scalar channel is also proportional to the chiral order parameter.

$$ \begin{aligned} \Delta_{S}^{disconnected} (q) & = \int d^{4}x e^{iqx} \left\langle \mathcal{T} \left(\bar{q} q(x) \bar{q} q(0)\right) \right\rangle_{disconnected}\\ & = \int d^{4}x e^{iqx} \frac{1}{4} \left\langle \text{Tr} \left[\left(i \gamma^{5} S(x,x) i \gamma^{5} -S(x,x) \right)\right] \right.\\&\quad\left.\text{Tr} \left[\left(S(0,0)- i \gamma^{5} S(0,0) i \gamma^{5} \right)\right] \right\rangle. \end{aligned} $$

(3)

The difference between the vector and axial vector with or without strangeness is also an order parameter. In this case with strangeness, the difference is proportional to the chiral symmetry breaking in both flavors.

$$ \begin{aligned} \Delta_{K^{*}-K_{1}}^{m} (q) & = \int d^{4}x e^{iqx} \left\langle \mathcal{T} \left(\bar{s} \gamma_{\mu} q(x) \bar{q} \gamma_{\mu} s(0)- \bar{s} \gamma^{5} \gamma_{\mu} q(x) \bar{q} \gamma^{5} \gamma_{\mu} s(0) \right)\right\rangle\\ & = \int d^{4}x e^{iqx} \frac{1}{2} \left\langle \text{Tr} \left[ \gamma_{\mu} \left(i\gamma^{5} S_{q}(x,0) i \gamma^{5} -S_{q}(x,0) \right) \gamma_{\mu}\right.\right.\\ &\quad\left.\left.\left(S_{s}(0,x)-i \gamma_{5} S_{s}(0,x) i \gamma_{5} S(0,x) \right) \right] \right\rangle, \end{aligned} $$

(4)

where the subscripts q,s in the propagator denote the flavor.

It should be noted that chiral partners in this case are between K^∗,K₁ with the same flavor structure. That is between $K^{*}(\bar {s}q), K_{1}(\bar {s}q)$ or between $K^{*}(\bar {q}s), K_{1}(\bar {q}s)$.

2.1 Weinberg sum rule

For two light quarks with different flavor, we obtain the Weinberg type sum rule [15]. In this case, the difference in Eq. (4) can be written as

$$\begin{array}{*{20}l} & (q_{\mu} q_{\nu}- g_{\mu \nu} q^{2}) \Pi^{V}-q_{\mu} q_{\nu} \Pi^{A}_{2} +g_{\mu \nu} \Pi^{A}_{1} \\ & = (q_{\mu} q_{\nu}- g_{\mu \nu} q^{2}) \frac{c}{Q^{6}} \langle \bar{q} q \rangle^{2}...+g_{\mu \nu} m \langle \bar{q} q \rangle, \end{array} $$

(5)

where c is the Wilson coefficients and the vacuum saturation is assumed for the 4-quark operators, which should be a good approximation as it is proportional to the chiral order parameter in this case. Here, $\Pi ^{V}, \Pi ^{A}_{1}$ have contributions from the vector meson and axial vector meson respectively, while $\Pi ^{A}_{2}$ has the additional contribution from the pions. By taking the first and second moments of the sum rule, we obtain the first two set of Weinberg sum rules.

$$\begin{array}{*{20}l} & f_{V}^{2} m_{V}^{2}-f_{A}^{2} m_{A}^{2} = f_{\pi}^{2}, ~~f_{V}^{2} m_{V}^{4}-f_{A}^{2} m_{A}^{4} = 0. \end{array} $$

(6)

One notes that when chiral symmetry is restored such that f_π→0, we have m_A=m_V. One can further assume the KSRF relation and obtain $m_{A} =\sqrt {2}m_{V}$. By multiplying Eq. (5) by q^μq^ν, we obtain the celebrated GOR relation $f_{\pi }^{2} m_{\pi }^{2} =\langle m \bar {q}q \rangle$. Looking at higher moments leads to $f_{V}^{2} m_{V}^{6}-f_{A}^{2} m_{A}^{6} =c \langle \bar {q} q \rangle ^{2}$

2.2 4-quark operators: ρ−a ₁ sector

For $J^{\rho }_{\mu } =\bar {q} \tau ^{3} \gamma _{\mu } q$ and $J^{a_{1}}_{\mu } =\bar {q} \tau ^{3} \gamma _{\mu } \gamma ^{5} q$ current, the relevant dimension 6 operators contributing to the transverse part of the correlation function, in the SU(2) flavor limit, are given as

$$\begin{array}{@{}rcl@{}} \Pi^{\rho} & = &\frac{2 \pi \alpha_{s}}{Q^{6}} \left\langle \left(\bar{q} \gamma_{\mu} \gamma^{5} \lambda^{a} \tau^{3} q \right)^{2} \right\rangle \\ &&+ \frac{4 \pi \alpha_{s}}{9Q^{6}} \left\langle \left(\sum_{ud} \bar{q} \gamma_{\mu} \lambda^{a} q \right)\left(\sum_{uds} \bar{q} \gamma_{\mu} \lambda^{a} q \right) \right\rangle, \\ \Pi^{a_{1}} & = &\frac{2 \pi \alpha_{s}}{Q^{6}} \langle (\bar{q} \gamma_{\mu} \lambda^{a} \tau^{3} q)^{2} \rangle \\ &&+ \frac{4 \pi \alpha_{s}}{9Q^{6}} \left\langle \left(\sum_{ud} \bar{q} \gamma_{\mu} \lambda^{a} q \right)\left(\sum_{uds} \bar{q} \gamma_{\mu} \lambda^{a} q \right) \right\rangle, \end{array} $$

(7)

3 U _A(1) breaking effect

There is a cautionary point when taking the difference of two correlation functions. Consider taking the difference between the scalar and pseudo-scalar currents in SU(2) for simplicity.

$$\begin{array}{*{20}l} &\Delta_{s-\eta}^{m} (q) \\ &\quad= \int d^{4}x e^{iqx} \langle \mathcal{T} \bigg(\bar{q} q(x) \bar{q} q(0)- \bar{q} i \gamma^{5} q(x) \bar{q} i \gamma^{5} q(0) \bigg) \rangle \!. \end{array} $$

(8)

This correlation has contributions from both the connected and disconnected diagrams. Also, the difference in the connected diagram is related to the chiral order parameter and does not vanish when chiral symmetry is broken. However, even when chiral symmetry is restored, there is a contribution that is related to the topologically non-trivial configuration and does not vanish [16]. These are the U_A(1) breaking effects and are related to the zero modes containing all flavors. The contribution can be well understood by looking at whether the effective instanton vertex contributes [17]. The effective vertex in the quark form is of the following form in SU(2).

$$\begin{array}{@{}rcl@{}} \det [\bar{q}_{R}q_.+h.c] \\ = \bigg(\bar{u}_{R} u_{L} \times \bar{d}_{R} d_{L}- \bar{u}_{R} d_{L} \times \bar{d}_{R} u_{L} +.h.c. \bigg). \end{array} $$

(9)

It is clear that this term interpolates between the currents and gives a non-vanishing contribution to Eq. (8). The form using the meson degrees of freedom has the following form.

$$\begin{array}{@{}rcl@{}} \det [\bar{q}_{R}q_{L}.+h.c] \propto \bigg(\sigma^{2}+\pi^{2}-\eta^{2} -\alpha^{2} \bigg). \end{array} $$

(10)

Hence, it is also clear that this equation will also give a non-vanishing contribution to Eq. (8).

4 K ₁ and K ^∗ mesons

The vector mesons and their widths are given in Table 1. The ρ and a₁ are chiral partners, but with large widths, any previous attempts to measure their mass shift seem futile. The ω and the f₁(1285) have small widths, but are isospin singlets and are not chiral partners as discussed in Ref. [18]. Still, in the limit where we neglect the flavor changing disconnected diagrams, they form chiral partners and hence experimental measurements are extremely useful as they provide input for extracting the density dependence of condensates. On the other hand, K^∗ and K₁ are chiral partners but also have reasonably small widths. Furthermore, their first excited states are already degenerate so that the chiral symmetry breaking effects seems to be concentrated in the ground states. Therefore, we will concentrate on K^∗ and K₁.

Table 1 Mass and width of vector and axial vector mesons. Units are in MeV

4.1 K ₁ and K ^∗ correlation functions

Let us look at the correlation functions for the K^∗ and K₁ mesons given in Ref [1]. The time-ordered current correlation function of the K^∗ or K₁ current is given by

$$\begin{array}{@{}rcl@{}} \Pi_{\mu \nu}(\omega, \mathbf{q})= i\int d^{4} x e^{iq\cdot x}\langle |T[j_{\mu}, \bar{j}_{\nu} ]|\rangle, \end{array} $$

(11)

where q^μ=(ω,q) and

$$\begin{array}{@{}rcl@{}} j_{\mu}^{K_{1}^{+}} = \bar{s} \gamma_{\mu} \gamma_{5} u &, & ~~~ j_{\mu}^{K_{1}^{-}} = \bar{u} \gamma_{\mu} \gamma_{5} s \\ j_{\mu}^{K^{*+}} = \bar{s} \gamma_{\mu} u &, &~~~ j_{\mu}^{K^{*-}} = \bar{u} \gamma_{\mu} s. \end{array} $$

(12)

We will not consider currents with d quarks as we will only consider symmetric matter so that the results would be the same as those with the u quarks.

As the currents are not conserved, the polarization function for both the vector and axial vector will have contributions from the scalar and pseudo-scalar mesons respectively. Furthermore, there will be transverse and longitudinal polarization in the medium. Here, we will only consider the limit where we take the external three-momentum to be zero q^μ=(ω,0). In this work, we will extract the vector and axial-vector parts by looking at the following projection.

$$\begin{array}{@{}rcl@{}} \frac{1}{3} (q^{\mu} q^{\nu}/q^{2}-g^{\mu \nu}) \Pi_{\mu \nu}(q) \stackrel{\mathbf{q} \rightarrow 0}{\longrightarrow} \Pi(\omega, 0). \end{array} $$

(13)

4.1.1 4-quark operators: K ^∗−K ₁ sector

Choosing $J^{K^{*}}_{\mu } =\bar {u} \gamma _{\mu } s$ and $J^{K_{1}}_{\mu } =\bar {u} \gamma _{\mu } \gamma ^{5} s$ currents, the relevant dimension 6 4-quark operators are given by

$$\begin{array}{*{20}l} \Pi^{K^{*}} & = \frac{2 \pi \alpha_{s}}{Q^{6}} \langle (\bar{u} \gamma_{\mu} \gamma^{5} \lambda^{a} s)(\bar{s} \gamma_{\mu} \gamma^{5} \lambda^{a} u) \rangle\\&\quad+ \frac{2 \pi \alpha_{s}}{9Q^{6}} \langle (\bar{s} \gamma_{\mu} \lambda^{a} s +\bar{u} \gamma_{\mu} \lambda^{a} u) (\bar{q} \gamma_{\mu} \lambda^{a} q) \rangle, \\ \Pi^{K_{1}} & = \frac{2 \pi \alpha_{s}}{Q^{6}} \langle (\bar{u} \gamma_{\mu} \lambda^{a} s)(\bar{s} \gamma_{\mu} \lambda^{a} u) \rangle\\&\quad+ \frac{2 \pi \alpha_{s}}{9Q^{6}} \langle (\bar{s} \gamma_{\mu} \lambda^{a} s +\bar{u} \gamma_{\mu} \lambda^{a} u) (\bar{q} \gamma_{\mu} \lambda^{a} q) \rangle. \\ \end{array} $$

(14)

4.1.2 Weinberg type of sum rule for K ₁,K ^∗

The difference between the correlation functions for the vector and axial vector currents has the following form up to dimension 6 operators

$$\begin{array}{*{20}l} & -\frac{2}{Q^{2}} m_{s} \langle\bar{u}u\rangle_{0} +\frac{2 \pi}{Q^{4}} \alpha_{s} \bigg(\langle (\bar{u} \gamma_{\mu} \lambda^{a} s)((\bar{s} \gamma_{\mu} \lambda^{a} u) \rangle - c.p \bigg) \\ & - \frac{8 \pi}{3Q^{6}}q^{\mu} q^{\nu} \alpha_{s} \bigg(\langle (\bar{u} \gamma_{\mu} \lambda^{a} s)((\bar{s} \gamma_{\nu} \lambda^{a} u) \rangle_{\mathcal{S}T} -c.p. \bigg), \end{array} $$

(15)

where c.p is obtained by replacing γ_μ→γ_μγ₅ in the 4-quark operator. The second line of Eq. (15) corresponds to the twist-4 matrix element. Since the difference in Eq. (15) is a chiral order parameter, the operators at all dimensions are proportional to the chiral symmetry breaking effects: $m_{s} \langle \bar {u} u \rangle$ at dimension 4 and $\langle \bar {s} s \rangle \langle \bar {u} u \rangle$ at dimension 6 after vacuum saturation. This is so because the difference is proportional to the chiral symmetry breaking parts in the strangeness sector multiplied by those in the light quark sector. Therefore, while the exact vacuum saturation hypothesis might be problematic, the fact that it should be proportional to the chiral order parameter remains valid. Therefore, even in a medium, one can estimate their changes by approximating their values in terms of the changes in the light and strange condensates as is typically done in the factorization formula for the 4-quark condensate in a medium.

The Weinberg type sum rule for the present case can be obtained by taking the difference in the K^∗ and K₁ correlation functions and keeping the lowest meson contribution while assuming the excited states and continuum contributions to cancel. Then, by looking at the lowest two non-trivial moments with scalar 4-quark operators only, we obtain the following Weinberg type sum rule for the strange sector.

$$\begin{array}{*{20}l} & f_{K^{*}}^{2} m_{K^{*}}^{4}-f_{K_{1}}^{2} m_{K_{1}}^{4} = - 2 m_{s} \langle \bar{u}u \rangle \\ & f_{K^{*}}^{2} m_{K^{*}}^{6}-f_{K_{1}}^{2} m_{K_{1}}^{6} = - \frac{64}{9} \pi \alpha_{s} \langle \bar{u}u \rangle \langle \bar{s}s \rangle, \end{array} $$

(16)

Combining these two relations, we obtain

$$\begin{array}{*{20}l} {}& f_{K^{*}}^{2} m_{K^{*}}^{4} (m_{K_{1}}^{2}-m_{K^{*}}^{2}) = -2 m_{s} \langle \bar{u}u \rangle m_{K_{1}}^{2} + \frac{64}{9} \pi \alpha_{s} \langle \bar{u}u \rangle \langle \bar{s}s \rangle. \end{array} $$

(17)

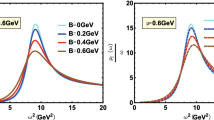
Hence, when chiral symmetry is restored, $m_{K_{1}}^{2}=m_{K^{*}}^{2}$. As the chiral order parameter is expected to be restored by 30% in nuclear matter, one expects to see a non-trivial change in the mass difference between $m_{K_{1}}$ and $\phantom {\dot {i}\!}m_{K^{*}}$. In a numerical analysis recently performed in Ref. [1], we find that the upper limit of the mass shift of $K_{1}^{-}$ ($K_{1}^{+}$) in nuclear matter is as large as − 249 (− 35) MeV.

5 Phenomenological observations

The dominant hadronic decay channels are given in Table 2. This means that with the kaon beam, the K^∗ (K₁) can be produced by the π (ρ) exchange with a nucleon.

Table 2 Dominant hadronic decay channels of K^∗ and K₁ meson

As discussed before, the chiral partnership between the K^∗ and K₁ exists between the same charge states. If a K⁻ beam is used to produce these particles, the expected final states for K₁ are given by

$$\begin{array}{*{20}l} K_{1}^{-} \to \left\{\begin{array}{l} \rho^{0} K^{-} \\ \rho^{-} \bar{K}^{0} \\ \pi^{0} K^{*-} \\ \pi^{-} \bar{K}^{* 0} \end{array}\right., ~~~~ \bar{K}_{1}^{0} \to \left\{\begin{array}{l} \rho^{+} K^{-} \\ \rho^{0} \bar{K}^{0} \\ \pi^{+} K^{*-} \\ \pi^{0} \bar{K}^{* 0} \end{array}\right., \end{array} $$

and for K^∗ by

$$\begin{array}{*{20}l} K^{*-} \to \left\{\begin{array}{l} \pi^{0} K^{-} \\ \pi^{-} \bar{K}^{0} \end{array}\right., ~~~~ \bar{K}^{*0} \to \left\{\begin{array}{l} \pi^{+} K^{-} \\ \pi^{0} \bar{K}^{0} \end{array}\right.. \end{array} $$

The production of both K^∗,K₁ will be possible by the Kaon beam at JPARC, and K^∗ by the pion beam at GSI [19]. If chiral symmetry is restored, the degeneracy of K^∗,K₁ mass will lead to similar numbers for the production of these partners at the hadronization point in a heavy ion collision. The number of K^∗ is found to be smaller than that predicted from the statistical hadronization model (SHM). This suppression is well understood as coming from hadronic scattering and decay during the hadronic phase [20, 21]. As the K₁ width is not so much larger than that of the K^∗, the reduction of its number during the hadronic phase should be similar to that of K^∗. Considering the much larger mass of K₁ in the vacuum, the number of K₁ will be larger than that expected from the SHM and similar to that of K^∗. Therefore measuring the number of K₁ from heavy ion collisions, although challenging, will provide a signature for chiral symmetry restoration in a heavy ion collision.

6 Conclusion

After decades-long attempts to measure the mass shift and understand the origin of hadron mass, it has become clear that one has to analyze hadrons with small vacuum width. Also, to identify the chiral symmetry breaking effects, one has to start by looking at chiral partners. Such considerations have inevitably led us to consider K^∗ and K₁ in matter [1]. In particular, with the kaon beam at JPARC, the possibility of observing both of these particles in a nuclear target experiment is quite feasible. The problem of final state interaction from hadronic decays can be overcome by including the study of excitation energy dependence [9]. Heavy ion experiments provide another venue to probe chiral symmetry restoration in the early stages of the collision. The degeneracy of the K^∗ and K₁ mass at the hadronization point will manifest as a large increase in the K₁ meson than expected from the SHM. Hence, measurement of the K₁ and K^∗ numbers in a heavy ion collision will therefore provide invaluable information on the masses at the chiral phase transition point. Once the masses and mass difference of K^∗ and K₁ mesons are measured, one will be closer to understanding the origin of the hadron masses and the effects of chiral symmetry breaking in their values. Finally, similar arguments can be made about the chiral partners in the charmed meson sector. However, the large charm quark mass makes it difficult to directly observe the effects in a nuclear target experiment. Still using an anti-proton beam on a nuclear target, one can use the proton anti-proton annihilation energy to produce charm and anti-charm with a smaller three momentum. This way, one can prolong the time the charmed meson propagates in medium and observe the mass modification. Such experiments can be done in PANDA or future JPARC.

This work was supported by Samsung Science and Technology Foundation under Project Number SSTF-BA1901-04.