Skip to main content
SpringerLink
Log in

Design and experimental study of a quasi-zero-stiffness vibration isolator incorporating transverse groove springs

  • Original Article
  • Published:
Archives of Civil and Mechanical Engineering Aims and scope Submit manuscript

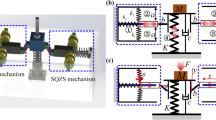
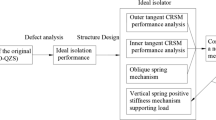
Abstract

The concept of quasi-zero-stiffness (QZS) vibration isolator was proposed in recent decades to improve the low-frequency isolation performance without increasing the static displacement. This work is devoted to the concrete realization of a QZS isolator by utilizing transverse groove springs. Firstly, the QZS isolator is theoretically analyzed and some dynamical indices are analytically calculated. Then, the transverse groove springs are designed and the isolator prototype is assembled; the QZS feature of the prototype is basically fulfilled. Finally, the experiments are conducted by means of an electrodynamic shaker which generates sinusoidal base excitation for the isolator prototype; the experimental results clearly show the good isolation performance of the QZS isolator and meanwhile reflect some practical factors that should be noticed in actual applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Demir C, Civalek Ö. Torsional and longitudinal frequency and wave response of microtubules based on the nonlocal continuum and nonlocal discrete models. Appl Math Model. 2013;37:9355–67.

    Google Scholar 

  2. Numanoglu HM, Akgöz B, Civalek Ö. On dynamic analysis of nanorods. Int J Eng Sci. 2018;130:33–50.

    Google Scholar 

  3. Akgöz B, Civalek Ö. Longitudinal vibration analysis for microbars based on strain gradient elasticity theory. J Vib Control. 2012;20:606–16.

    MathSciNet  Google Scholar 

  4. Fiebig W, Wróbel J. Two stage vibration isolation of vibratory shake-out conveyor. Arch Civ Mech Eng. 2017;17:199–204.

    Google Scholar 

  5. Chen SB, Xuan M, Xin J, Liu Y, Gu S, Li J, Zhang L. Design and experiment of dual micro-vibration isolation system for optical satellite flywheel. Int J Mech Sci. 2020;179:105592.

    Google Scholar 

  6. Deng CC, Mu DQ, Guo JL, Xie P. Reducing the negative effects of flywheel disturbance on space camera image quality using the vibration isolation method. Front Optoelectron. 2017;10:80–8.

    Google Scholar 

  7. Oh HU, Lee KJ, Jo MS. A passive launch and on-orbit vibration isolation system for the spaceborne cryocooler. Aerosp Sci Technol. 2013;28:324–31.

    Google Scholar 

  8. Sitharam TG, Sebastian R, Fazil F. Vibration isolation of buildings housed with sensitive equipment using open trenches–Case study and numerical simulations. Soil Dyn Earthq Eng. 2018;115:344–51.

    Google Scholar 

  9. Li Q, Zhao JC. Experimental study on the vibration isolation characteristics of hydraulic engine mounts. Exp Tech. 2010;34:34–9.

    Google Scholar 

  10. Bai XX, Jiang P, Qian LJ. Integrated semi-active seat suspension for both longitudinal and vertical vibration isolation. J Intell Mater Syst Struct. 2016;28:1036–49.

    Google Scholar 

  11. Ibrahim RA. Recent advances in nonlinear passive vibration isolators. J Sound Vib. 2008;314:371–452.

    Google Scholar 

  12. Shaw AD, Neild SA, Wagg DJ, Weaver PM, Carrella A. A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation. J Sound Vib. 2013;332:6265–75.

    Google Scholar 

  13. Li H, Zhang J. Design and analysis of a magnetic QZS vibration isolator. Appl Mech Mater. 2013;470:484–8.

    Google Scholar 

  14. Carrella A, Brennan MJ, Waters TP. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J Sound Vib. 2017;301:678–89.

    Google Scholar 

  15. Carrella A, Brennan MJ, Waters TP. Optimization of a quasi-zero-stiffness isolator. J Mech Sci Technol. 2007;21:946–9.

    Google Scholar 

  16. Carrella A, Brennan MJ, Kovacic I, Waters TP. On the force transmissibility of a vibration isolator with quasi-zero stiffness. J Sound Vib. 2009;322:707–17.

    Google Scholar 

  17. Carrella A, Brennan MJ, Waters TP, Lopes V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int J Mech Sci. 2012;55:22–9.

    Google Scholar 

  18. Carrella A, Friswell MI, Zotov A, Ewins DJ, Tichonov A. Using nonlinear springs to reduce the whirling of a rotating shaft. Mech Syst Signal Process. 2009;23:2228–35.

    Google Scholar 

  19. Kovacic I, Brennan MJ, Waters TP. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. J Sound Vib. 2008;315:700–11.

    Google Scholar 

  20. Ramirez DFL, Ferguson NS, Brennan MJ, Tang B. An experimental nonlinear low dynamic stiffness device for shock isolation. J Sound Vib. 2015;347:1–13.

    Google Scholar 

  21. Liu CR, Yu KP. Accurate modelling and analysis of a typical nonlinear vibration isolator with quasi-zero stiffness. Nonlinear Dyn. 2020;10:10. https://doi.org/10.1007/s11071-020-05642-2.

    Article  Google Scholar 

  22. Zhou JX, Wang XL, Xu DL, Bishop S. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam–roller–spring mechanisms. J Sound Vib. 2015;346:53–69.

    Google Scholar 

  23. Sun XT, Jing XJ. A nonlinear vibration isolator achieving high-static-low-dynamic stiffness and tunable anti-resonance frequency band. Mech Syst Signal Process. 2016;80:166–88.

    Google Scholar 

  24. Liu CC, Jing XJ, Chen ZB. Band stop vibration suppression using a passive X-shape structured lever-type isolation system. Mech Syst Signal Process. 2016;68–69:342–53.

    Google Scholar 

  25. Meng LS, Sun JG, Wu WJ. Theoretical design and characteristics analysis of a quasi-zero stiffness isolator using a disk spring as negative stiffness element. Shock Vib. 2015;2015:813763.

    Google Scholar 

  26. Carrella A, Brennan MJ, Waters TP, Shin K. On the design of a high-static–low-dynamic stiffness isolator using linear mechanical springs and magnets. J Sound Vib. 2008;315:712–20.

    Google Scholar 

  27. Zheng YS, Zhang XN, Luo YJ, Yan B, Ma CC. Design and experiment of a high-static–low-dynamic stiffness isolator using a negative stiffness magnetic spring. J Sound Vib. 2016;360:31–52.

    Google Scholar 

  28. Dong GX, Zhang XN, Xie SL, Yan B, Luo YJ. Simulated and experimental studies on a high-static-low-dynamic stiffness isolator using magnetic negative stiffness spring. Mech Syst Signal Process. 2017;86:188–203.

    Google Scholar 

  29. Zheng YS, Zhang XN, Luo YJ, Zhang YH, Xie SL. Analytical study of a quasi-zero stiffness coupling using a torsion magnetic spring with negative stiffness. Mech Syst Signal Process. 2018;100:135–51.

    Google Scholar 

  30. Robertson WS, Kidner MRF, Cazzolato BS, Zander AC. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation. J Sound Vib. 2009;326:88–103.

    Google Scholar 

  31. Li Q, Zhu Y, Xu DF, Hu JC, Min W, Pang LC. A negative stiffness vibration isolator using magnetic spring combined with rubber membrane. J Mech Sci Technol. 2013;27:813–24.

    Google Scholar 

  32. Liu XT, Huang XC, Hua HX. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. J Sound Vib. 2013;332:3359–76.

    Google Scholar 

  33. Huang XC, Liu XT, Hua HX. On the characteristics of an ultra-low frequency nonlinear isolator using sliding beam as negative stiffness. J Mech Sci Technol. 2014;28:813–22.

    Google Scholar 

  34. Kovacic I, Brennan MJ, Lineton B. Effect of a static force on the dynamic behaviour of a harmonically excited quasi-zero stiffness system. J Sound Vib. 2009;325:870–83.

    Google Scholar 

  35. Wang K, Zhou JX, Xu DL. Sensitivity analysis of parametric errors on the performance of a torsion quasi-zero-stiffness vibration isolator. Int J Mech Sci. 2017;134:336–46.

    Google Scholar 

  36. Abolfathi A, Brennan MJ, Waters TP, Tang B. On the effects of mistuning a force-excited system containing a quasi-zero-stiffness vibration isolator. J Vib Acoust. 2015;137:044502.

    Google Scholar 

  37. Hao ZF, Cao QJ, Wiercigroch M. Nonlinear dynamics of the quasi-zero-stiffness SD oscillator based upon the local and global bifurcation analyses. Nonlinear Dyn. 2017;87:987–1014.

    Google Scholar 

  38. Hao ZF, Cao QJ, Wiercigroch M. Two-sided damping constraint control strategy for high-performance vibration isolation and end-stop impact protection. Nonlinear Dyn. 2016;86:2129–44.

    MathSciNet  Google Scholar 

  39. Dong GX, Zhang YH, Luo YJ, Xie SL, Zhang XN. Enhanced isolation performance of a high-static–low-dynamic stiffness isolator with geometric nonlinear damping. Nonlinear Dyn. 2018;93:2339–56.

    Google Scholar 

  40. Liu CR, Yu KP. Superharmonic resonance of the quasi-zero-stiffness vibration isolator and its effect on the isolation performance. Nonlinear Dyn. 2020;100:95–117.

    Google Scholar 

  41. Valeev A. Dynamics of a group of quasi-zero stiffness vibration isolators with slightly different parameters. J Low Freq Noise Vib Act. 2018;37:640–53.

    Google Scholar 

  42. Kovacic I, Lenci S. Externally excited purely nonlinear oscillators: insights into their response at different excitation frequencies. Nonlinear Dyn. 2018;93:119–32.

    Google Scholar 

  43. Wang XL, Zhou JX, Xu DL, Ouyang HJ, Duan Y. Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness. Nonlinear Dyn. 2017;87:633–46.

    Google Scholar 

  44. Wang Y, Li SM, Neild SA, Jiang JZ. Comparison of the dynamic performance of nonlinear one and two degree-of-freedom vibration isolators with quasi-zero stiffness. Nonlinear Dyn. 2017;88:635–54.

    Google Scholar 

  45. Liu CR, Yu KP. A high-static–low-dynamic-stiffness vibration isolator with the auxiliary system. Nonlinear Dyn. 2018;94:1549–67.

    Google Scholar 

  46. Sun XT, Jing XJ. Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity. Mech Syst Signal Process. 2015;62–63:149–63.

    Google Scholar 

  47. Liu CR, Yu KP, Pang SW. A novel eight-legged vibration isolation platform with dual-pyramid-shape struts. Meccanica. 2019;54:873–99.

    MathSciNet  Google Scholar 

  48. Zhou JX, Xiao QY, Xu DL, Ouyang HJ, Li YL. A novel quasi-zero-stiffness strut and its applications in six-degree-of-freedom vibration isolation platform. J Sound Vib. 2017;394:59–74.

    Google Scholar 

  49. Zhu T, Cazzolato B, Robertson WSP, Zander A. Vibration isolation using six degree-of-freedom quasi-zero stiffness magnetic levitation. J Sound Vib. 2015;358:48–73.

    Google Scholar 

  50. Lan CC, Yang SA, Wu YS. Design and experiment of a compact quasi-zero-stiffness isolator capable of a wide range of loads. J Sound Vib. 2014;333:4843–58.

    Google Scholar 

  51. Le TD, Ahn KK. Experimental investigation of a vibration isolation system using negative stiffness structure. Int J Mech Sci. 2013;70:99–112.

    Google Scholar 

  52. Huang XC, Liu XT, Sun JY, Zhang ZY, Hua HX. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: a theoretical and experimental study. J Sound Vib. 2014;333:1132–48.

    Google Scholar 

  53. Fulcher BA, Shahan DW, Haberman MR, Seepersad CC, Wilson PS. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. J Vib Acoust. 2014;136:031009.

    Google Scholar 

  54. Wu WJ, Chen XD, Shan YH. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. J Sound Vib. 2014;333:2958–70.

    Google Scholar 

  55. Xu DL, Yu QP, Zhou JX, Bishop SR. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic. J Sound Vib. 2013;332:3377–89.

    Google Scholar 

  56. Lu ZQ, Yang TJ, Brennan MJ, Liu ZG, Chen LQ. Experimental investigation of a two-stage nonlinear vibration isolation system with high-static-low-dynamic stiffness. J Appl Mech. 2017;84:021001.

    Google Scholar 

  57. Hao ZF, Cao QJ. The isolation characteristics of an archetypal dynamical model with stable-quasi-zero-stiffness. J Sound Vib. 2015;340:61–79.

    Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 11372084), which is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Department of Astronautic Science and Mechanics, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China

    Chaoran Liu & Kaiping Yu

Authors
  1. Chaoran Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kaiping Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kaiping Yu.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of the paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Yu, K. Design and experimental study of a quasi-zero-stiffness vibration isolator incorporating transverse groove springs. Archiv.Civ.Mech.Eng 20, 67 (2020). https://doi.org/10.1007/s43452-020-00069-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s43452-020-00069-3

Keywords

Search

Navigation