Algebraic Stability Analysis of Particle Swarm Optimization Using Stochastic Lyapunov Functions and Quantifier Elimination

Abstract

This paper adds to the discussion about theoretical aspects of particle swarm stability by proposing to employ stochastic Lyapunov functions and to determine the convergence set by quantifier elimination. We present a computational procedure and show that this approach leads to a reevaluation and extension of previously known stability regions for PSO using a Lyapunov approach under stagnation assumptions.

Introduction

Particle swarm optimization (PSO) is a nature-inspired computational model that was originally developed by Kennedy and Eberhart [36] to simulate the kinetics of birds in a flock. Meanwhile, PSO developed into a class of widely used bio-inspired optimization algorithms and thus the question of theoretical results about stability and convergence became important [5, 8, 9, 16, 18, 40]. Generally speaking, a PSO defines each particle as a potential solution of an optimization problem with an objective function $f:\mathbb {R}^d \rightarrow \mathbb {R}$ defined on a d-dimensional search space. The PSO depends on three parameters, the inertial, the cognitive, and the social weight. Apart from a theoretical interest, stability analysis of PSO is mainly motivated by finding which combinations of these parameters promote convergence. Asymptotic stability of the PSO implies convergence to an equilibrium point, which may be connected with, but not necessarily guarantees, finding a solution of the underlying optimization problem. In other words, while generally speaking PSO stability can be regarded as a proxy for PSO convergence, for a given objective function the relationships between stability and convergence can be much more complicated  [17, 28]. It was empirically shown that PSOs with theoretically unstable parameters perform worse than a trivial random search across various objective functions with varying dimensionality [13, 14, 17], but the selection of PSO parameters which show good performance is highly dependent on the objective function. Just as for some functions the theoretical stability region overestimates the convergence region, there are other functions for which parameters can be selected just outside of the stability region without reducing the performance considerably [28].

In essence, PSO defines a stochastic discrete-time dynamical system. The stochasticity may be regarded as to come from two related sources. The primary source is that the prefactors of the cognitive and the social weight are realizations of a random variable, usually with a uniform distribution on the unit interval. A secondary source is that the sequences of local and global best positions are also effected by random as they reflect the search dynamics of the PSO caused by the interplay between the primary source of randomness and the objective function. Thus, these sequences can also be modeled as realizations of a random variable, but with a non-stationary distribution as the search dynamics modifies the influence of the primary source of randomness. Most of the existing works on PSO stability focus on the primary source of randomness and assume stagnation in the sequences of personal and global best positions. Lately, there are some first attempts to incorporate the secondary source of random as well with stability analysis of stagnating and non-stagnating distribution assumptions [8, 18].

The stability of PSO implies that the sequence of particle positions remains bounded and some quantities calculated from this sequence converge to target values. This has been done under the so-called deterministic assumption in which omitting random leads to deterministic stability analysis [5, 6, 20, 55]. If the random drive of the PSO is included in the analysis, then stochastic quantities evaluating the sequence of particle positions could be the expected value, or variance, or even skewness and kurtosis, which leads to order-1 [46, 47], order-2 [8, 14, 16, 40], and order-3 [25] stability. Basically, conditions for boundedness and convergence of PSO sequences can be obtained by different mathematical methods. The first group of methods focuses on the dynamical system’s aspects of the PSO and uses Lyapunov function arguments for stability analysis [5, 29, 35, 55]. Another group of methods explicitly addresses the stochastic character of the PSO and relies on non-homogenous recurrence relations [8, 46] and convergence of a sequence of bounded linear operators [18].

A stability analysis using Lyapunov function arguments is particularly interesting from a dynamical system’s point of view as the method provides a mathematically direct way to derive stability conditions on system parameters without solving the system of difference equations. Lyapunov functions can be thought of as generalized energy functions and give us the possibility to make conclusions about the behavior of the trajectories of the system without explicitly finding the trajectories. We are thus able to formally prove stability properties. This is a contrast to the stochastic approach to PSO convergence such as order-1 or order-2 stability which requires the convergence of stochastic quantities evaluating the sequence of particle positions to constant values without directly taking into account the system’s dynamics. Lyapunov function methods are known to give rather conservative results and applications to PSO stability have indeed shown rather restrictive stability regions [35, 55]. On the other hand, stochastic stability of the system’s motion is in some ways a stronger requirement than the convergence of stochastic quantities. This has relevance to the discussion as empirical results have shown that the stability region calculated by the stochastic approach, particularly the region found by Poli and Jiang [34, 46, 47], for some objective functions overestimates the experimentally obtained convergence region [13,14,15].

For obtaining a proof of stability for the system’s motion, while also attenuating the conservatism of the Lyapunov approach to PSO stability, we propose in this paper an analysis consisting of two steps. First, we employ stochastic Lyapunov functions [23, 29, 38, 52] and subsequently determine the convergence set by quantifier elimination [49, 50]. A main feature of such an analysis is that it is an algebraic approach relying entirely on symbolic computations. Any vagueness with respect to the selection of parameter values, which is commonly connected with numerical calculations, is absent. Quantifier elimination allows to treat a class of Lyapunov function candidates at once and thus leads to a diminished conservatism. It is shown that the convergence set we obtain by such a procedure gives a reevaluation and extension of previously known stability regions for PSO using a Lyapunov approach under stagnation assumptions.

The paper is organized as follows. In the next section, we give a brief description of the PSO and discuss the mathematical description we use for the stability analysis. The stability analysis based on stochastic Lyapunov functions is given in the subsequent section. It follows how the convergence set can be calculated by quantifier elimination. The convergence region obtained by the computational procedure proposed in this paper, together with a comparison to existing results, is given before the final section. The paper is concluded with a summary of the findings and some pointers to future work.

Particle Swarm Optimization

Let $\varGamma (t)$ be a set of N particles in $\mathbb {R}^d$ at a discrete-time step t; we also call $\varGamma (t)$ the particle swarm at time $t \in \mathbb {N}_0$, with $\mathbb {N}_0 :=\lbrace 0,1,2,\ldots \rbrace$. Each particle is moving with an individual velocity and depends on a memory or feedback information about its own previous best position (local memory) and the best position of all particles (global memory). The individual position at the next time-step $t+1$ results from the last individual position and the new velocity. Each particle is updated independently of others and the only link between the dimensions of the problem space is introduced via the objective function. Because the stagnation assumption implies loosing the objective function linkage, we can analyze the one-dimensional-one-particle case and keep the general case.

The general system equations [5, 15, 35, 47] in the one-dimensional case are

$$\begin{aligned} x(t+1)&= x(t) + v(t+1) \end{aligned}$$

(1)

$$\begin{aligned} v(t+1)&= wv(t)+c_1r_1(t)(p^\mathrm{{l}}(t) - x(t)) \nonumber \\&\quad +c_2r_2(t)(p^\mathrm{{g}}(t) - x(t)) , \end{aligned}$$

(2)

where x(t) is the position and v(t) is the velocity at time step t. The best local and global position is represented by $p^\mathrm{{l}}$ and $p^\mathrm{{g}}$; w is the inertial weight. The random variables $r_1(t),r_2(t): \mathbb {N}_0 \rightarrow \mathcal {U}\left[ 0,1 \right]$ are uniformly distributed. The parameters $c_1$ and $c_2$ are known as cognitive and social weights and scale the interval of the uniform distribution, i.e. $c_1r_1(t) \sim \mathcal {U}\left[ 0,c_1 \right]$.

Previous works analyzed the stability with the substitution

$$\begin{aligned} \theta&= \theta ^{(\mathrm{{l}})} + \theta ^{(\mathrm{{g}})} = c_1r_1(t) + c_2r_2(t) \end{aligned}$$

(3)

$$\begin{aligned} p&= \frac{\theta ^{(\mathrm{{l}})}p^{(\mathrm{{l}})} + \theta ^{(\mathrm{{g}})}p^{(\mathrm{{g}})}}{\theta }, \end{aligned}$$

(4)

where $\theta$ is a constant [6, 20, 55]. This is known as the deterministic assumption. Thus, the simplified system definition in state-space form

$$\begin{aligned} \begin{pmatrix} x_{t+1} \\ v_{t+1} \end{pmatrix} = \begin{pmatrix} 1-\theta &{} w\\ -\theta &{} w \end{pmatrix} \begin{pmatrix} x_t \\ v_t \end{pmatrix} + \begin{pmatrix} \theta \\ \theta \end{pmatrix}p \end{aligned}$$

(5)

can be reformulated as a linear time-invariant second-order system whose stability analysis is a straightforward application of linear theory.

In Kadirkamanathan et al. [35], the system is reformulated as a linear time-invariant second-order system with nonlinear feedback, which relates to Lure’s stability problem, see e.g. [37], p. 264. The nonlinear feedback is described by the parameter $\theta , 0<\theta <c_1+c_2$. The global best value p is considered as another state variable in the state vector $z=\begin{pmatrix}x_t-p \\ v_t\end{pmatrix}$. The assumption $p=p^\mathrm{{l}}=p^\mathrm{{g}}$ applies to the time-invariant case. This results in the following linear state space model:

$$\begin{aligned} \begin{pmatrix} x_{t+1}-p \\ v_{t+1} \end{pmatrix} =&\begin{pmatrix} 1 &{} w\\ 0 &{} w \end{pmatrix} \begin{pmatrix} x_t-p \\ v_t \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \end{pmatrix}u_t \end{aligned}$$

(6)

$$\begin{aligned} y_t =&\begin{pmatrix}1&1\end{pmatrix} \begin{pmatrix} x_t-p \\ v_t \end{pmatrix} \end{aligned}$$

(7)

$$\begin{aligned} u_t =&-\theta y_t. \end{aligned}$$

(8)

Later, Gazi [29] used the system definition (6) and (7) and derived a convergence region using a stochastic Lyapunov function approach. The proof of stability is based upon a positive real argument for absolute stability in connection with Tsypkin’s stability result [42].

In the following stability analysis, we adopt the description (6) and (7) of the PSO as a linear time-discrete, time-invariant stochastic system and obtain

$$\begin{aligned} z(t+1)=A z(t) + B z(t) r(t) + C u(t) r(t), \end{aligned}$$

(9)

where $z=\begin{pmatrix}x&v\end{pmatrix}^\mathrm{{T}}$ is the state-vector with n states, A a $n\times n$ matrix for the deterministic and B a $n\times n$ matrix for the stochastic part of the state-space system. The input matrix C transfers the system input u(t) and r(t), which is a uniformly distributed random variable of the stochastic system.

To avoid the loss of uniform distribution through a linear combination with different parameters $c_1,c_2$ of the random variables $r_1(t),r_2(t)$ in Eq. (3), the adjustment

$$\begin{aligned} \theta _1&=\theta _1^\mathrm{{l}}+\theta _1^\mathrm{{g}}= cr_1(t)+cr_2(t),&\text {with } c_1 = c_2 \end{aligned}$$

(10)

$$\begin{aligned} \theta _2&=\theta _2^\mathrm{{l}}+\theta _2^\mathrm{{g}}= c_1r(t)+c_2r(t) ,&\text {with } c_1 \ne c_2 \end{aligned}$$

(11)

is used, which can be interpreted as a convolution of two uniform distributions. With the assumptions (10) and (11), we can define two systems which both follow the structure of Eq. (9):

$$\begin{aligned}&\mathbf{System 1: }\nonumber \\ \varSigma _1&={\left\{ \begin{array}{ll} A_1=\begin{pmatrix} 1 &{} \omega \\ 0 &{} \omega \end{pmatrix} \\ B_1=\begin{pmatrix} -c &{} 0 \\ -c &{} 0 \end{pmatrix}\\ C_1=\begin{pmatrix} c &{} c \end{pmatrix} \\ r(t)= r_1(t)+r_2(t)\\ u(t)=\frac{\theta _1^\mathrm{{l}}p^\mathrm{{l}}(t) + \theta _1^\mathrm{{g}}p^\mathrm{{g}}(t)}{\theta _1} \end{array}\right. } \end{aligned}$$

(12)

$$\begin{aligned}&\mathbf{System 2: }\nonumber \\ \varSigma _2&={\left\{ \begin{array}{ll} A_2=\begin{pmatrix} 1 &{} \omega \\ 0 &{} \omega \end{pmatrix}\\ B_2=\begin{pmatrix} -(c_1+c_2) &{} 0 \\ -(c_1+c_2) &{} 0 \end{pmatrix}\\ C_2=\begin{pmatrix} (c_1+c_2) &{} (c_1+c_2) \end{pmatrix}\\ r(t)= r(t)\\ u(t)=\frac{\theta _2^\mathrm{{l}}p^\mathrm{{l}}(t) + \theta _2^\mathrm{{g}}p^\mathrm{{g}}(t)}{\theta _2}. \end{array}\right. } \end{aligned}$$

(13)

In the following analysis, we assume stagnation: $p^\mathrm{{l}}(t) = p^\mathrm{{l}}$, and $p^\mathrm{{g}}(t) = p^\mathrm{{g}}$. In this case, we obtain a constant $E\lbrace u(t) \rbrace = \text {const.}$, which allows us to shift with the help of a coordinate transformation the state of system (9) such that $E\lbrace u(t) \rbrace = 0$. Thus, we obtain from the PSO system (9) the following expression:

$$\begin{aligned} z(t+1) = A_i z(t)+ B_i z(t) r(t). \end{aligned}$$

(14)

During stagnation, it is assumed that each particle behaves independently. This means that each dimension is treated independently and the behavior of the particles can be analyzed in isolation.

This linear discrete-time time-invariant system with multiplicative noise was studied in [32, 48] treating the linear-quadratic regulator problem and other control problems. Previous literature [29, 35] used the assumption (11) as a simplification of (10). In the following, we will show that the two systems with the assumptions (10) and (11) are not equivalent in the case of convergence, see also [19] for a recent discussion of similar results .

Lyapunov Based Stability Analysis

Lyapunov Methods in the Sense of Itô

Lyapunov methods are very powerful tools from modern control theory used in analyzing dynamical systems. Many important results of deterministic differential equations have been generalized to stochastic Itô processes [3, 43, 44] and Lyapunov methods to analyze stochastic differential equations developed from a theoretical side as well as in practical application [7, 23, 52], e.g. by investigating the convergence of Neural Networks and Evolutionary Algorithms. In the case of time-discrete nonlinear stochastic systems, there exists a stability theory equivalent to the continuous case. Incipient with some linear stochastic time-discrete systems [26, 32, 48], this goes over to nonlinear stochastic time-discrete systems [45] and proposals of a general theory for nonlinear stochastic time-discrete systems [38] for different stability definitions. This enables the application of Lyapunov methods to arbitrary random distributions.

A general definition of discrete-time nonlinear stochastic systems is:

$$\begin{aligned} z(t+1) = f(z(t),r(t),t), \; \; z(t_0)=z_0, \end{aligned}$$

(15)

where r(t) is a one-dimensional stochastic process defined on a complete probability space $(\varOmega , F, Pr)$, where $\varOmega$ is the sample space, F the event space and Pr the probability function. The vector $z_0 \in R^n$ is a constant vector for any given initial value $z(t_0) = z_0 \in R^n$. It is assumed that $f(0,r(t),t)\equiv 0, \forall t \in \lbrace t_0 + t : t \in \mathbb {N}_0 \rbrace$ with $\mathbb {N}_0 :=\lbrace 0,1,2,\ldots \rbrace$, such that system (15) has the solution $z(t) \equiv 0$ for the initial value $z(t_0) = 0$. This solution is called the trivial solution or equilibrium point. We assume that f(z(t), r(t), t) satisfies a Lipschitz condition, which ensures the existence and uniqueness of the solution almost everywhere [51].

There are various stability definitions for discrete-time nonlinear stochastic systems.

Definition 1

(Stochastic stability) The trivial solution of system (15) is said to be stochastically stable or stable in probability iff for every $\epsilon >0$ and $h>0$, there exists $\delta = \delta (\epsilon ,h,t_0)>0$, such that

$$\begin{aligned} Pr\lbrace \vert z(t) \vert < h\rbrace \ge 1 - \epsilon , \; \; t \ge t_0, \end{aligned}$$

(16)

when $\vert z_0 \vert < \delta$. Otherwise, it is said to be stochastically unstable.

Definition 2

(Asymptotic stochastic stability) The system (15) is asymptotically stochastically stable if the system is stochastically stable in probability according to Definition 1, and for every $\epsilon > 0$, $h>0$, there exists $\delta = \delta (\epsilon ,h,t_0)>0$, such that

$$\begin{aligned} \mathrm{{Pr}}\Big \lbrace \lim \limits _{t \rightarrow \infty }{z(t)} = 0\Big \rbrace \ge 1 - \epsilon , \; \; t \ge t_0, \end{aligned}$$

(17)

when $\vert z_0 \vert < \delta$.

These stability definitions do not only imply boundedness and convergence of trajectories generated by a stochastic dynamical system (15), they explicitly require an attractive set of initial states, described by $\delta = \delta (\epsilon ,h,t_0)>0$, from which bounded and converging trajectories start. This constitutes a stronger requirement than just bounds on stochastic operators, which are on the core of a PSO stability analysis leading to order-1, order-2, and order-3 stability. As the stochastic Lyapunov stability analysis is based on these stronger stability definitions it also leads to stronger stability guarantees.

To find some mathematical criteria that satisfy these definitions, a stability criterion of discrete-time stochastic systems is next given with a mathematical expectation of the probability mass function [38].

Theorem 1

(Stochastic stability) The system (15) is stable in probability if there exist a positive-definite function V(z(t)), such that $V(0)=0$, $V(z(t))>0 \; \; \forall z(t)\ne 0$ and

$$\begin{aligned} E \lbrace \varDelta V(z(t)) \rbrace \le 0 \end{aligned}$$

(18)

for all $z(t) \in R^n$. The function V is called a Lyapunov function.

The proof of Theorem 1 (as well as the following Theorem  2 dealing with asymptotic stability) is shown in [38].

Theorem 2

(Asymptotic stochastic stability) The system (15) is asymptotically stable in probability if there exists a positive-definite function V(z(t)) and a non-negative continuous strictly increasing function $\gamma (\cdot )$ from $R_+$ to $\infty$, with $\gamma (0)=0$ such that it vanishes only at zero and

$$\begin{aligned} E \lbrace \varDelta V(z(t)) \rbrace \le -\gamma (\vert z(t) \vert ) < 0 \end{aligned}$$

(19)

for all $z(t) \in R^n \backslash \{0\}$. The function V is called a Lyapunov function.

Applying the Lyapunov Method to PSO

Consider the quadratic Lyapunov function candidate

$$\begin{aligned} V=z(t)^\mathrm{{T}}Pz(t) \end{aligned}$$

(20)

with a real symmetric positive-definite $2 \times 2$ matrix

$$\begin{aligned} P =\begin{pmatrix} p_1 &{} p_2 \\ p_2 &{} p_3 \\ \end{pmatrix}. \end{aligned}$$

(21)

The values of the elements in P have significant impact on the shape and the size of the obtained stability region. This matrix is positive-definite if the elements of the matrix $\lbrace p_1,p_2,p_3\rbrace \in P$ satisfy the Sylvester criterion [53]

$$\begin{aligned} p_1&> 0 \end{aligned}$$

(22)

$$\begin{aligned} p_1p_3-p^2_2&> 0. \end{aligned}$$

(23)

According to Theorem 2, the system (14) is said to be asymptotically stable in probability if

$$\begin{aligned} E\lbrace \varDelta V(z(t))\rbrace < 0. \end{aligned}$$

(24)

Thus, we can define the Lyapunov difference equation of system (14) with the function candidate (20) as

$$\begin{aligned} \varDelta V(z(t))&= V(z(t+1))-V(z(t)) \nonumber \\&= \left( A z(t) + B z(t)\right) ^\mathrm{{T}} P \left( A z(t) + B z(t)\right) \nonumber \\&\quad - z(t)^\mathrm{{T}}Pz(t) \nonumber \\&= z(t)^\mathrm{{T}}(A^\mathrm{{T}} P A + A^\mathrm{{T}} P B \nonumber \\&\quad + B^\mathrm{{T}} P A + B^\mathrm{{T}} P B -P)z(t), \end{aligned}$$

(25)

and obtain

$$\begin{aligned} E\lbrace \varDelta V(z(t))\rbrace&=E\lbrace z(t)^\mathrm{{T}}(A^\mathrm{{T}} P A + A^\mathrm{{T}} P B + B^\mathrm{{T}} P A \nonumber \\&\quad + B^\mathrm{{T}} P B -P) z(t)\rbrace < 0. \end{aligned}$$

(26)

We replace $A=A_i$ and $B=B_i$ as the Lyapunov difference equation applies for both system definitions expressed by Eq. (14). Formally, we can describe the expectation of $\varDelta V(z(t))$ with

$$\begin{aligned} E\lbrace \varDelta V(z(t))\rbrace = \sum _{i=1}^{n} \sum _{j=1} ^{n}\varDelta V(x_i,v_j) \cdot \mathrm{{Pr}}(x_i,v_j). \end{aligned}$$

(27)

The variable n denotes the number of states, which is $n=2$ in our case. Unfortunately, the sums cannot be calculated directly because we do not know the distribution of $\mathrm{{Pr}}(x,v)$, which is non-stationary and changes for every time-step. Therefore, we approximate the expectation (27) by calculating the expectation of the kth moments of the known uniformly distributed random variable $r(t)\sim \mathcal {U}[0,1]$. This can be written as

$$\begin{aligned} E\lbrace \varDelta V(x,v)\rbrace = \varDelta V(x,v\vert E\lbrace r\rbrace ,E\lbrace r^2\rbrace , \ldots ,E\lbrace r^k\rbrace ). \end{aligned}$$

(28)

We thus get the expected value for $E\lbrace \varDelta V(x,v)\rbrace$ by the expectation of the random variable of $E\lbrace r\rbrace$ and its kth moments. The rationale of this approximation is that by considering with $k=1,2$ the first and second moment we obtain results which can be compared to results for order-1 and order-2 stability [8, 14, 16, 40, 46].

We applied a quadratic Lyapunov function candidate (20) such that we calculate up to the second moment. This can be done if we consider

$$\begin{aligned} E\lbrace \varDelta V(z(t))\rbrace&= E\lbrace V(z(t+1))\rbrace - V(z(t)) \nonumber \\&= z(t)^\mathrm{{T}}(A^T P A-P + A^\mathrm{{T}} P B^* \nonumber \\&\quad + B^{^*\mathrm{{T}}} P A + E\lbrace B^\mathrm{{T}} P B \rbrace )z(t), \end{aligned}$$

(29)

where $B^*$ includes the first and $E\lbrace B^\mathrm{{T}} P B \rbrace$ the second moment of the random variable r(t). The order of the Lyapunov function candidate depends on the order of the moment for calculating the expectation of the random variable r(t). For $\varSigma _1$ (12), we can determine the expectation

$$\begin{aligned} B_1^*=E \lbrace B r(t) \rbrace&= \begin{pmatrix} -c &{} 0 \\ -c &{} 0 \end{pmatrix} E \lbrace r(t) \rbrace \nonumber \\&= \begin{pmatrix} -1 &{} 0 \\ -1 &{} 0 \end{pmatrix} E \lbrace cr(t) \rbrace \end{aligned}$$

(30)

with $E \lbrace cr(t) \rbrace = c(E \lbrace r_1(t) \rbrace +E \lbrace r_2(t) \rbrace ) = c(\frac{1}{2}+ \frac{1}{2})=c$. Furthermore, we calculate the expectation of the squared random variable r(t)

$$\begin{aligned} E \lbrace B^\mathrm{{T}} P B \rbrace&= \begin{pmatrix} -c^2r^2(p_1+2p_2+p_3) &{} 0 \\ 0 &{} 0 \end{pmatrix} \nonumber \\&= \begin{pmatrix} p_1+2p_2+p_3 &{} 0 \\ 0 &{} 0 \end{pmatrix} E \lbrace c^2r^2(t) \rbrace \end{aligned}$$

(31)

with $E \lbrace c^2r^2(t) \rbrace = c^2(E \lbrace r_1(t) \rbrace +E \lbrace r_2(t) \rbrace )^2 = \frac{7}{6}c^2$. With these expectations we get for the difference equation of the Lyapunov candidate, Eq. (25), and $\varSigma _1$:

$$\begin{aligned} E\lbrace \varDelta V(z(t))\rbrace&= \varDelta V\left( z(t)\vert E\lbrace r(t)\rbrace , E\lbrace r^2(t) \rbrace \right) \nonumber \\&= v^2\left( -p_3 + \left( p_1+2p_2+p_3\right) w^2\right) \nonumber \\&\quad - 2vx \Big (p_2 +w\big (\left( -1+c\right) p_1 \nonumber \\&\quad +\left( -1+2c\right) p_2+cp_3\big )\Big ) \nonumber \\&\quad + x^2 \frac{1}{6}c\big (\left( -12+7c\right) p_1+\left( -6+7c\right) 2p_2 \nonumber \\&\quad + 7 c p_3\big ). \end{aligned}$$

(32)

For $\varSigma _2$ (13), we can determine the expectation with

$$\begin{aligned} B_2^*=E \lbrace B r(t) \rbrace&= \begin{pmatrix} -(c_1+c_2) &{} 0 \\ -(c_1+c_2) &{} 0 \end{pmatrix} E \lbrace r(t) \rbrace \nonumber \\&= \begin{pmatrix} -1 &{} 0 \\ -1 &{} 0 \end{pmatrix} E \lbrace (c_1+c_2)r(t) \rbrace , \end{aligned}$$

(33)

and $E \lbrace (c_1+c_2)r(t) \rbrace = (E \lbrace c_1r(t) \rbrace +E \lbrace c_2r(t) \rbrace ) = \frac{(c_1+c_2)}{2}$. The expectation of the term $B^\mathrm{{T}} P B$ can be expressed as follows:

$$\begin{aligned} E \lbrace B^\mathrm{{T}} P B \rbrace&= \begin{pmatrix} (c_1+c_2)^2r^2(p_1+2p_2+p_3) &{} 0 \\ 0 &{} 0 \end{pmatrix} \nonumber \\&= \begin{pmatrix} p_1+2p_2+p_3 &{} 0 \\ 0 &{} 0 \end{pmatrix} E \lbrace (c_1+c_2)^2r^2 \rbrace . \end{aligned}$$

(34)

Furthermore, the expectation in the expression (34) is calculated by

$$\begin{aligned} E \lbrace (c_1+c_2)^2r^2 \rbrace&= E \lbrace \left( \left( c_1+c_2\right) r \right) ^2 \rbrace \nonumber \\&= \left( E \lbrace c_1 r\rbrace + E \lbrace c_2 r \rbrace \right) ^2 \nonumber \\&= E \lbrace c_1 r\rbrace ^2 + 2E \lbrace c_1c_2 r\rbrace ^2+E \lbrace c_2 r\rbrace ^2 \nonumber \\&= \frac{1}{3}\left( c_1^2 + 2 c_1 c_2 + c_2^2 \right) . \end{aligned}$$

(35)

Now we can formulate the expectation of the difference equation of the Lyapunov candidate, Eq. (25),

$$\begin{aligned} E\lbrace \varDelta V(z(t))\rbrace&= \varDelta V\left( z(t)\vert E \lbrace (c_1+c_2)r(t) \rbrace , E \lbrace (c_1+c_2)^2r^2 \rbrace \right) \nonumber \\&= \frac{1}{3} \Big (3 v^2 ( - p_3 + ( p_1 + 2p_2 + p_3) w^2) \nonumber \\&\quad - 3vx \big (2 p_2 + w( \left( -2 + c_1 + c_2\right) p_1 \nonumber \\&\quad + 2\left( -1 + c_1 + c_2\right) p_2 + \left( c_1+c_2\right) p_3)\big )\nonumber \\&\quad + x^2\left( c_1 + c_2 \right) \big ( \left( -3 +c_1 +c_2\right) p_1 - 3 p_2 \nonumber \\&\quad + \left( c_1 + c_2\right) \left( 2 p_2 + p_3 \right) \big )\Big ). \end{aligned}$$

(36)

Determining the Convergence Set

Based on the Eqs. (32) and (36), the convergence set can be computed. To this end, we are looking for parameter constellations $(c_1+c_2)$ or $(c,\omega )$ for which the parameters $p_1,p_2,p_3$ specifying the quadratic Lyapunov function candidate (20) exist such that the resulting matrix P, as defined by Eq. (21), is positive definite and the condition $E\lbrace \varDelta V(z(t))\rbrace <0$ holds in Eqs. (32) and (36). Technically, this can be expressed using existential ($\exists$) and universal ($\forall$) quantifiers, which gives

$$\begin{aligned} \exists p_1,p_2,p_3: E\lbrace \varDelta V(z(t))\rbrace <0 \wedge p_1>0 \wedge p_1p_3-p_2^2>0, \end{aligned}$$

(37)

again to apply for Eq. (32) as well as for Eq. (36). Unfortunately, this expression does not permit a constructive and algorithmic way for the convergence set analysis. We are rather looking for a description of the set without quantifiers. A very powerful method to achieve such a description is the so-called quantifier elimination (QE). Before we continue with the determination of the convergence set using this technique, let us briefly introduce some necessary notions and definitions, see also [49, 50].

Equations (32) and (36) can be generalized using the prenex formula

$$\begin{aligned} G(y,z):=(Q_1 y_1)\cdots (Q_l y_l)\,F(y,z), \end{aligned}$$

(38)

with $Q_i \in \left\{ \exists , \forall \right\}$. The formula F(y, z) is called quantifier-free and consists of a Boolean combination of atomic formulas

$$\begin{aligned} \varphi (y_1\dots ,y_l,z_1,\dots ,z_k) \,\tau \, 0, \end{aligned}$$

(39)

with $\tau \in \{=,\ne ,<,>,\le ,\ge \}$. In our case, we have the prenex formula (37), the quantifier-free formulas $E\lbrace \varDelta V(z(t))\rbrace <0 \wedge p_1>0 \wedge p_1p_3-p_2^2>0$, the atomic formulas $E\lbrace \varDelta V(z(t))\rbrace <0$, $p_1>0$ and $p_1p_3-p_2^2>0$ as well as the quantified variables $y=\{p_1,p_2,p_3\}$ and the free variables $z=\{c_1+c_2,\omega \}$. We are now interested in a quantifier-free expression H(z) which only depends on the free variables. The following theorem states that such an expression always exists [4, pp. 69–70].

Theorem 3

(Quantifier elimination over the real closed field) For every prenex formula G(y, z) there exists an equivalent quantifier-free formula H(z).

The existence of such a quantifier-free equivalent was first proved by Alfred Tarski [54]. He also proposed the first algorithm to realize such a quantifier elimination. Unfortunately, the computational load of this algorithm cannot be bounded by any stack of exponentials (see, e.g. [31] for details). This means complexity measures grow much faster than exponential and thus such an algorithm does not apply to non-trivial problems. The first employable algorithm is the cylindrical algebraic decomposition (CAD) [21]. This procedure contains four phases. First, the space is decomposed in semi-algebraic sets called cells. In every cell, we have for every polynomial in the quantifier-free formula F(y, z) a constant sign. These cells are gradually projected from $\mathbb {R}^n$ to $\mathbb {R}^1$. These projections are cylindrical, which means that projections of two different cells are either equivalent or disjoint. Furthermore, every cell of the partition is a connected semi-algebraic set and thus algebraic. Based on the achieved interval conditions the prenex formula is evaluated in $\mathbb {R}^1$. The result is afterward lifted to $\mathbb {R}^n$. This leads to the sought quantifier-free equivalent H(z). Although the procedure has, in the worst case, a doubly exponential complexity [24], CAD is the most common and most universal algorithm to perform QE.

The second prevalent strategy to solve QE problems is virtual substitution [41, 56, 57]. At the beginning, the innermost quantifier of a given prenex formula is changed to $\exists y_i$ using $\forall y: F(y) \iff \lnot (\exists y: \lnot F(y))$. Based on so-called elimination sets a formula equivalent substitution is used to solve $\exists y: F(y)$. This is iterated until all quantifiers are eliminated. Virtual substitution can be applied to polynomials up to the order of three. Its computational complexity rises exponentially with the number of quantified variables.

The third frequently used strategy is based on the number of real roots in a given interval. Due to Sturm–Habicht sequences a real root classification can be performed [30, 33, 59]. This approach can lead to very effective QE algorithms. Especially for so-called sign definite conditions ($\forall y: y\ge 0 \implies f(y)>0$) a very high performance is available. In this case, the complexity grows exponentially with just the degree of the considered polynomials. While CAD results are simple output formulas, the ones resulting of virtual substitution and real root classification are generally very complex and redundant. Hence, a subsequent simplification is needed.

During the last decades, some powerful tools to handle QE problems became available. The first tool which was applicable to non-trivial problems is the open source package Quantifier Elimination by Partial Cylindrical Algebraic Decomposition (QEPCAD) [22]. The subsequent tool QEPCAD B [10] is available in the repositories of all common Linux distributions. The packages Reduce and Redlog are open-source as well and further contain virtual substitution based algorithms. This also holds for Mathematica. The library RegularChains [11, 12] gives a quiet efficient CAD implementation for the computer-algebra-system Maple. Finally, Maple provides the software package SyNRAC [2, 58], which contains CAD, virtual substitution and real root classification based algorithms.

Computational Results and Comparison of Different Convergence Regions

The following computational results are obtained by the Maple Package SyNRAC [2, 58]. As mentioned before the used algorithms are very sensitive concerning the number of considered variables. Fortunately, the chosen Lyapunov candidate function gives a possibility for reduction. From the Eqs. (22) and (23), we can see that the elements of the principal diagonal need to be positive ($p_1, p_3 >0$). Furthermore, the conditions we are verifying are inequalities, cf. Eq. (26). These inequalities can be scaled with some positive factor $\beta$ without loss of generality. We can describe such a scaling by matrices $\beta P$. In other words, the matrix $\tilde{P}=\beta P,\, \beta >0$ leads to the same results as the matrix P. With this property we can normalized the matrix P to an element of the principal diagonal, that is, we can set $p_1$ or $p_3$ to unity. This reduces the search space by one dimension.

Nevertheless, the computational complexity involved in the elimination process leads to the necessity of a further restriction of the search space. In fact, with the computational resources available to us, we could only handle three quantified variables. Since the quantified variables x and v need to be eliminated for useful statements, we are thus able to quantify one variable of $P=\left( \begin{matrix} p_1 &{} p_2 \\ p_2 &{} p_3 \end{matrix} \right)$, that is either $p_1, p_2$ or $p_3$. The variable $p_2$ occurs twice in the matrix P. This results in more complex prenex formulas, especially with more terms of high degree, concerning the quantified variables. Considering this limitations, we setup three candidates of P for our experiments.

At first, we compute the quantifier-free formula with

$$\begin{aligned} P^*_1=\mathbb {I}, \end{aligned}$$

(40)

with the identity matrix $\mathbb {I}$. The quantifiers to be eliminated are, therefore, limited to the universal quantifier $\forall x,v$. In addition, we were able to compute the quantifier-free formula with

$$\begin{aligned} P^*_2 =\begin{pmatrix} p_1 &{} 0 \\ 0 &{} p_3 \\ \end{pmatrix}, \end{aligned}$$

(41)

which makes it necessary to eliminate additionally the existence quantifier $\exists p_1,p_3$ and

$$\begin{aligned} P^*_3 =\begin{pmatrix} 1 &{} p_2 \\ p_2 &{} 1 \\ \end{pmatrix}, \end{aligned}$$

(42)

with two instances of the existence quantifier $\exists p_2$. As discussed above, the three matrices (40)–(42) represent all possible candidate matrices P with two free variables. This means $P=\beta \mathbb {I}$ in matrix (40) or $P=\left( \begin{matrix} 1 &{} 0 \\ 0 &{} p_3 \end{matrix} \right)$ in matrix (41) or $P=\left( \begin{matrix} \beta &{} p_2 \\ p_2 &{} \beta \end{matrix} \right)$ in matrix (42), each with $0<\beta < \infty$, leads to the same results.

For all further computations we study the convergence set with $c > 0$ and $w \in (-1,1)$. Every convergence expression reported below adheres to these conditions. The convergence set for $\varSigma _1$ using the conditions (37) yields for $P^*_1$ the quantifier-free formula

$$\begin{aligned} H(c,\omega )=(7c -6<0)\wedge (2 c^2 w^2 - 3 w^2 - 7 c^2 + 6 c >0) \end{aligned}$$

(43)

for $P^*_2$ there is

$$\begin{aligned}&H(c,\omega ) \nonumber \\&\quad =(c < \text {root}_i (49 c^2 + 48 w_i^2 c - 168 c + 24 w_i^4 - 168 w_i^2 + 144)) \end{aligned}$$

(44)

and for $P^*_3$ the convergence set is

$$\begin{aligned}&H(c,\omega ) \nonumber \\&\quad =(7c -6<0)\wedge (7 c^2 - 24 w c - 6 c + 24 w^2 + 12 w - 12 < 0). \end{aligned}$$

(45)

Calculating the convergence set for $\varSigma _2$ using the condition (37) leads for $P^*_1$ to the quantifier-free formula

$$\begin{aligned}&H(c_1+c_2,\omega )= (2(c_1 +c_2) -3\le 0) \wedge \nonumber \\&\quad (w^2(c_1 +c_2)^2-2(c_1 +c_2)^2+3(c_1 +c_2)-3w^2\ge 0), \end{aligned}$$

(46)

while for $P^*_2$ the convergence set is

$$\begin{aligned}&H(c_1+c_2,\omega )= (3w^2+(c_1 +c_2) -3\le 0) \wedge \nonumber \\&\quad (3w^4+3w^2(c_1 +c_2) \nonumber \\&\qquad +(c_1 +c_2)^2-12w^2-6(c_1 +c_2)+9\ge 0), \end{aligned}$$

(47)

and for $P^*_3$, we have

$$\begin{aligned}&H(c_1+c_2,\omega )=(2 (c_1+c_2) - 3 \le 0) \wedge \nonumber \\&\quad (2 (c_1+c_2)^2 - 12 w (c_1+c_2) \nonumber \\&\qquad - 3 (c_1+c_2) + 24 w^2 + 12 w - 12 \le 0). \end{aligned}$$

(48)

Fig. 1

Set of all parameter constellations assuring convergence in $\varSigma _1$

Fig. 2

Set of all parameter constellations assuring convergence in $\varSigma _2$

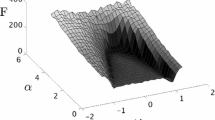
The resulting set of parameters assuring convergence is illustrated in Fig. 1 for $\varSigma _1$ and in Fig. 2 for $\varSigma _2$. The expression (44) is an indexed root expression. An indexed root expression $\text {root}_i$ can be written as

$$\begin{aligned} \lbrace z_k \rbrace \;\tau \; \text {root}_i\varphi ( z_1,\dots ,z_k). \end{aligned}$$

(49)

It is true at a point $(\alpha _1, \ldots , \alpha _k) \in \mathbb {R}^k$. In our case, the expression (44) are true for $i=\lbrace 2,3\rbrace$. In Fig. 3, we can see exemplary the set of all indexed root expressions $\text {root}_i$ of the convergence set (44). According to the constraints of $c>0$ and $w \in (-1,1)$, the solution of $\text {root}_2$ and $\text {root}_3$ bound the convergence region for $\varSigma _1$.

We can interpret these regions, shown in Fig. 1 and in Fig. 2, as the union of possible solutions $\{p_1,p_2,p_3\} \in \mathbb {R}^3$, respecting the definiteness constraints, that is $p_1>0$ and $p_1p_3-p_2^2>0$. In other words, by considering $p_1$, $p_2$ and $p_3$ as quantified variables, we handle all numeric values at once, which includes the identity matrix. Thus, the result for the identity matrix ($P_1^*$) gives a subset of $P_2^*$ as well as of $P^*_3$. With $P_2^*$ and $P_3^*$ either the quantifier $\exists p_1, p_3$ or $\exists p_2$ are eliminated. Under the definiteness constraints we either get a solution for all possible $p_1$ and $p_3$ (but $p_2=0$) or all possible $p_2$ (but $p_1=p_3=1$). Thus, $P_2^*$ and $P_3^*$ do not generalize each other and produce regions that partly overlap and partly differ. If in the future more powerful computational resources allow to eliminate all three existence quantifiers at once, the resulting region should contain both the area for $P_2^*$ and $P_3^*$, thus generalizing the results given here.

We further observe that generally for $\varSigma _1$ and $\varSigma _2$ the convergence region calculated with $P_1^*$ is also a subset of the regions calculated with $P_2^*$ and $P^*_3$. The area calculated for $\varSigma _2$ with $P_1^*$ leads to an expression with a quadratic polynomial and the region calculated with $P_2^*$ leads to an expression with a bi-quadratic polynomial, where the convergence set is axisymmetric with respect to the $c=c_1+c_2$-axis. However, the derived region with $P^*_3$ possesses a point symmetry, for $\varSigma _1$ at point $\left( c,w \right) =\left( \frac{3}{7},0\right)$ and for $\varSigma _2$ at the point $\left( c_1+c_2,w \right) =\left( \frac{3}{4},0\right)$. We can consider the convergence regions for the considered matrices P in union. The union can be carried out because each region was derived under the same constraints and fulfills the stability condition according to Eq. (37), such that they do not contradict each other. In addition, the matrices (41) and (42) each provided all possible instances of $p_1$ and $p_3$, or $p_2$, respectively. Thus, the non-overlapping regions calculated for $P^*_2$ and $P^*_3$ add to each other and thus results in a whole convergence set. This leads to a stability region with a horn-like bulge. An elimination of $p_1$, $p_2$ and $p_3$ should produce a generalized result which includes both $P^*_2$ and $P^*_3$ and thus cancels the bulge.

Fig. 3

Set of all roots of expression (44) for $\varSigma _1$ with the convergence region

We can finally set for $\varSigma _2$, $c_1+c_2 = c$ and compare $\varSigma _1$ and $\varSigma _2$. We can see that $\varSigma _1$ is nearly a subset of $\varSigma _2$. Only in the first quadrant a small triangle is not shared (see Fig. 4). The reason for formulating two systems is avoiding the loss of uniform distribution through a linear combination in the system definition, see Eqs. (10) and (11). Maintaining the uniform distribution was important for calculating the expectation. Now we see that the simplification $c=c_1+c_2$ turns to another expectation and also another convergence set.

In the past, there were several approaches to derive the convergence region of particle swarms under different stagnation assumptions [8, 9, 15, 16, 18]. In Fig. 4, we show our results as compared with other theoretically derived regions. Exemplary, we relate the results given by Eqs. (43)–(48) to the findings of Kadirkamanathan et al. [35]:

$$\begin{aligned} H(c,w)=c<2(1+w) \wedge c < \frac{2(1-w)^2}{1+w} \end{aligned}$$

(50)

and Gazi [29]:

$$\begin{aligned} H(c,w)= c< \frac{24 (1 - 2 \vert w \vert + w^2)}{7 (1 + w)}, \end{aligned}$$

(51)

with $w\in (-1,1)$. Both stability regions are calculated according to the system definition (6) and (7) and both are also based on using Lyapunov function approaches. Kadirkamanathan et al. [35] used a deterministic Lyapunov function and interpreted the stochastic drive of the PSO as a nonlinear time-varying gain in the feedback path, thus solving Lure’s stability problem. Gazi [29] used a stochastic Lyapunov approach and calculated the convergence set by a positive real argument for absolute stability following Tsypkin’s result.

Finally, we compare with the result of Poli and Jiang [34, 46, 47]:

$$\begin{aligned} H(c,w)=c<\frac{24(1-w^2)}{7-5w}, \end{aligned}$$

(52)

which is calculated as the stability region under the stagnation assumption but with the second moments of the PSO sampling distribution. The same stability region (52) has also been derived under less restrictive stagnation assumptions, for instance for weak stagnation [40], stagnate and non-stagnate distributions [8, 18].

We now relate these theoretical results on stability regions to each other. From Fig. 4, we can see that the $\varSigma _2$ formulation proposed in this paper, Eqs. (47) and (48), contains the whole convergence region derived by Kadirkamanathan et al. [35], see Eq. (50), and intersects with the region proposed by Gazi [29], see Eq. (51). We first consider the region proposed by Gazi [29] and our approach with $\varSigma _2$, which are both based on stochastic Lyapunov functions. Comparing the blue (Gazi) and the black ($\varSigma _2$) curve in Fig. 4, it can be seen that there is a substantial overlap, but also that $\varSigma _2$, especially by the derived convergence set with $P^*_2$, is more bulbous and expand more in the first quadrant. Under consideration of the derived region by the matrix $P^*_3$, we see one sub-region between $c\in (1,1.5)$ which expands the derived convergence region computed by $P^*_2$ additionally with a small triangle. The region from Gazi is more elongated and extends longer for larger values of $c_1+c_2$ and small values around $w=0$. In terms of area, we have $A= 3.44$ for $\varSigma _2$ and $A= 2.65$ for Gazi. Both regions share about 98% (with respect to the Gazi-region), but the $\varSigma _2$ region is also about 23% ($23.09 \%$) larger.

Moreover, $\varSigma _2$ is a subset of inequality (52), which is the convergence set first calculated by Poli and Jiang and later re-derived by others under different stagnation assumptions [8, 18, 34, 40, 46, 47]. In fact, $\varSigma _2$ is about 33% ($33.56\%$) smaller that the region expressed by Eq. (52). This, however, does not imply that the result is inferior. There are two reasons for this. A first is that the region expressed by Eq. (52) is calculated using a stochastic approach, which is methodological different from the Lyapunov function approach discussed in this paper. The second reason is that numerical experiments with a multitude of different objective functions from the CEC 2014 problem set [39] have shown that the region expressed by Eq. (52) at least for some functions overestimates the numerical convergence properties of practical PSO [13,14,15]. This particularly applies to the apex of the region (52), that is for $w\approx 0.5$ and $c_1+c_2 \approx 3.9$. The convergence region is smaller than Eq. (52) or “the rate of convergence is prohibitively slow”, [13], p. 34.

As discussed above, the different stability regions are calculated using different mathematical techniques. The Poli–Jiang region (52) is calculated based on bounds on stochastic operators, while $\varSigma _1$ and $\varSigma _2$ are regions of asymptotic stochastic Lyapunov stability. The latter is a stronger requirement than the former. Thus, the Poli–Jiang region (52) can be seen as an upper theoretical approximation of the PSO stability region, while the regions obtained by the Lyapunov approach give lower theoretical approximations. The numerical analysis showing the Poli–Jiang region (52) overestimating the convergence region for some objective functions also supports such a view [13,14,15]. From this, we may conjecture that the “real” region is between these approximations. Thus, the main feature of the stochastic Lyapunov approach in connection with quantifier elimination is the enlargement of the lower approximation. In principle, with the Lyapunov function method in connection with quantifier elimination an exact calculation of the stability region can be achieved by finding the correct class of Lyapunov function candidates.

Fig. 4

Comparison of different theoretically derived convergence regions

Conclusion

In this paper, we introduce a stochastic Lyapunov approach as a general method to analyze the stability of particle swarm optimization (PSO). Lyapunov function arguments are interesting from a dynamical system’s point of view as the method provides a mathematically direct way to derive stability conditions on system parameters. The method gives stronger stability guarantees as bounds on stochastic operators, which is used in stochastic approaches to PSO stability. However, it is also known to provide rather conservative results. We present a computational procedure that combines using a stochastic Lyapunov function with computing the convergence set by quantifier elimination (QE). Thus, we can show that the approach leads to a reevaluation and extension of previously known stability regions for PSO using Lyapunov approaches under stagnation assumptions. By employing the matrices (40)–(42) for quadratic Lyapunov function candidates, we search a generic parameter space. It represents all possible candidate matrices P with two free quantified variables. The union of all possible solutions of the considered matrices presents the derived convergence set (cf. Fig. 4), respecting the stability constraints and the system assumptions. However, the computational resources currently allow the elimination of two quantified variables only. With the elimination of all possible three quantified variables the resulting region should contain both the area for $P_2^*$ and $P_3^*$, thus generalizing the results given here and with that, the horn-like bulge visible in Fig. 4 for both system descriptions $\varSigma _1$ and $\varSigma _2$ should disappear.

The result is also relevant for reassessing the convergence region calculated by the stochastic approach to obtain order-1 and order-2 stability, particularly the region found by Poli and Jiang [34, 46, 47]. The Poli–Jiang region is larger than the stability region obtained by our approach and can be seen as an upper theoretical approximation of the PSO stability region. As it has been shown that for some objective functions this upper approximation overestimates the experimentally obtained convergence region [13,14,15], our result gives an improved lower approximation. By calculating quantifier-free formulas with QE, we additionally receive new analytical descriptions of the convergence region of two different system formulations of the PSO. The main difference to existing regions, apart from the size, is that the formulas describing them are more complex, with polynomial degrees up to quartic.

The method presented offers to extend studying PSO stability even more. We approximated the distribution of $\mathrm{{Pr}}(x,v)$ by the expectation of the random variable $E\lbrace r^k \rbrace$. Another way is to calculate the so-called second-order moment of $\mathrm{{Pr}}(x,v)$ [46, 47]. The stochastic Lyapunov approach in connection with QE could also be applied to second-order moments of $\mathrm{{Pr}}(x,v)$. We observed that there is a relation between the order of the Lyapunov candidate and the order of moments of the random variable. Thus, second-order moments can be accounted for by using Lyapunov function candidates of an order higher than quadratic.

Another possible extension is to treat PSO without stagnation assumptions [8, 18]. This requires to consider the expected value of the sequences of local and global best positions, which results in another multiplicative term in the expectation of $\varDelta V(x,v)$. Again, this could be accommodated by higher order Lyapunov function candidates. The main problem currently is that higher order Lyapunov function candidates also mean more variables that need to be eliminated by the QE. As of now, we could only handle, with the computational resources available to us, one quantified variable from the parameters of the Lyapunov function candidates, besides the system state $z=(x,v)$. This means an extension of the method proposed in this paper also relies upon further progress in computational hardware and efficient quantifier elimination implementations. In this context, it is worth mentioning that the problem is not solvable by improved hardware alone. Experiments with different hardware have shown that more powerful hardware reduces the run-time, but does not prevent the software from terminating without results. We think that the problem may be solvable with improved QE software. Currently, there are several promising attempts towards such improvements [1, 27].