Skip to main content
SpringerLink
Log in

Regression Modelling on Reliability Variation of a Parallel Series System of (m, ni) Order with Addition and Removal of Parallel Paths

  • Original Article
  • Published:
Journal of Statistical Theory and Practice Aims and scope Submit manuscript

Abstract

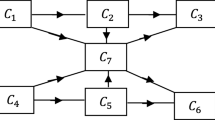
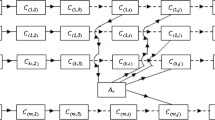
A regression model is fitted on variation of reliability of parallel series system of (m, ni) order (called initial system) by adding (or removing) the arbitrary number of parallel paths. The initial system is transformed by adding (or removing) the ‘p’ (or ‘k’) parallel paths. A reliability variation method is devised to obtain directly the reliability of the transformed system in terms of reliability of the initial system and reliability of the added (or removed) system. The variation in reliability is evaluated in both cases to see the effect of parallel paths on initial system reliability. Also, the variation in reliability of a particular parallel series system of order (4, 1) is obtained by assuming constant failure rate of the components. The effect of parallel paths and failure rate of the components on variation of reliability of the system is examined by fitting the linear regression model. The values of R2 and adjusted R2 are calculated to see the best fit of the model in order reduce the computing efforts to obtain the reliability of the transformed system. The results are shown numerically and graphically. The application of the study is discussed with justification.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig.10
Fig.11

Similar content being viewed by others

References

  1. Balagurusamy E (1984) Reliability engineering. Tata McGraw Hill Publishing Co. Ltd., New York

    Google Scholar 

  2. Benkamra Z, Terbeche M, Tlemcani M (2012) An allocation scheme for estimating the reliability of a parallel-series system. Adv Decis Sci 212:289035:1-289035:14

    MathSciNet  MATH  Google Scholar 

  3. Benkamra Z, Terbeche M, Tlemcani M (2013) Bayesian sequential estimation of the reliability of a parallel-series system. Appl Math Comput 219(23):10842–10852

    MathSciNet  MATH  Google Scholar 

  4. Epstein B, Sobel M (1954) Some theorems relevant to life testing from an exponential distribution. Ann Math Stat 25(2):373–381

    Article  MathSciNet  Google Scholar 

  5. Ezzati G, Rasouli A (2015) Evaluation system reliability using linear-exponential distribution function. Int J Adv Stat Prob 3(1):15–24

    Article  Google Scholar 

  6. Gupta AK, Zeng WB, Wu Y (2010) Probability and statistical models. Birkhäuser Basel, New York

    Book  Google Scholar 

  7. Montgomery DC, Peck EA, Vinning GG (2013) Introduction to linear regression analysis. Wiley, New York

    Google Scholar 

  8. Nitika A, Chauhan SK, Malik SC (2018) Reliability analysis of a non-series parallel system with different flow of information and Weibull failure laws. Int J Stat ReliabEng 5(1):22–30

    Google Scholar 

  9. Sharma KK, Bhutani RK (1992) Bayesian reliability analysis of a parallel system. ReliabEngSystSaf 37(3):227–230

    Google Scholar 

  10. Sharma MK (2014) Reliability analysis of a non-series parallel network in fuzzy and possibility context. Int J EducSci Res Rev 1(2):40–46

    Google Scholar 

Download references

Acknowledgements

The 1st author of the paper is very thankful to the Department of Science and Technology (DST), New Delhi for providing financial assistance under INSPIRE Fellowship Scheme. The authors are grateful to the reviewers for suggesting effective and technical valuable comments which enable us to make the work given in this manuscript more meaningful and worthy.

Author information

Authors and Affiliations

  1. Department of Statistics, M.D. University, Rohtak, India

    Nitika Ahlawat & S. C. Malik

Authors
  1. Nitika Ahlawat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. C. Malik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nitika Ahlawat.

Ethics declarations

Conflict of Interest

The work is original and has not been submitted anywhere for publication.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahlawat, N., Malik, S.C. Regression Modelling on Reliability Variation of a Parallel Series System of (m, ni) Order with Addition and Removal of Parallel Paths. J Stat Theory Pract 15, 28 (2021). https://doi.org/10.1007/s42519-020-00155-y

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42519-020-00155-y

Keywords

Search

Navigation