Channel flow of MHD bingham fluid due to peristalsis with multiple chemical reactions: an application to blood flow through narrow arteries

Abstract

The present analysis emphasizes the effects of variable properties on Bingham fluid under MHD peristaltic transport. Due to the impact of mechanical forces on the applied magnetic field on the conducting fluid, the fluid stream gets altered. These principle targets drug transport and control of blood flow during surgeries; hence the impact of MHD flow with convective and porous boundary conditions is considered. Further, the implications of homogeneous and heterogeneous reactions are analyzed by considering wall properties. The governing equations are turned dimensionless by appropriate similarity transformations. The series solution is obtained for temperature, velocity, and concentration by perturbation method with lubrication approach. The graphical representation of the pertinent parameters on the physiological flow quantities is depicted by applying for MATLAB 2019b program. The obtained results reveal that the rise in the magnetic parameter diminishes the velocity and temperature profiles. Further, the impact of variable viscosity slightly improves the magnitude of the trapped bolus. The homogenous and heterogeneous reaction parameters have a converse effect on the concentration distribution. Moreover, the present investigation finds its applications to perceive the complex rheological functioning of blood flow through narrow arteries.

1 Introduction

The peristalsis process induces the fluid flow through a duct due to the waves generated along the wall, as observed in the human gastrointestinal tract. Here, the ball of food, usually known as a bolus, is propelled because of the smooth muscle tissues’ sequential contraction and relaxation. Latham [1] has coined the idea of fluid transport employing peristaltic waves in mechanical and physiological studies. Usha and Ramachandra [2] have analyzed the peristaltic transport in various physiological situations of interest and concluded that the peristaltic waves always increase the mean flow rate for power-law fluids. Hamid et al. [3] studied the micropolar fluid's nonlinear peristaltic motion, assuming long wavelength and moderate Reynolds number. Solving the governing partial differential equation by FEM revealed that the micropolar parameter enhances the pressure rise in the pumping region. The study by Eldesoky et al. [4] signifies the consequences of slip conditions at the boundaries, the dynamic behavior of wall properties, and relaxation time on the motion of viscous non-Newtonian Maxwell fluid employing peristalsis. Recently [5] analyzed the importance of slip conditions on peristalsis in different configurations.

The flow of various fluids accompanied by MHD is widely used in MHD generators, geothermal field, aerospace engineering, astrophysics, nuclear reactors, medicine, engineering, and petroleum processes. Flow-through channels with the MHD field have grabbed interest because of its wide applications in the human organ system and medical engineering fields. Recently, the widespread use of the flow of magnetic particles under peristalsis, seen in magnetic pumping of blood, drug targeting, casting process, reduction of bleeding during surgery and magneto-therapy, etc., has captivated many researchers. Driven by MHD's application on biological fluids, Reddy [6] analyzed the velocity slip outcomes on the MHD porous peristaltic motion under mass and heat transfer. Reddy and Kattamreddy [7] considered the permeable peristaltic channel to study the consequences of velocity slip and Joule heating on the MHD motion under chemical reaction. Both [6, 7] inferred that the slip parameter elucidates the temperature and velocity fields. The curved complex wavy channel inspected by Javid et al. [8] to analyze the magnetic effects under peristaltic flow came out with results applicable to the manufacturing / improving the peristaltic instruments. They observed a decline in the pressure rise amplitude when the fluid relocates to a straight channel from the curved channel. Manjunath et al. [9] studied the motion of a Jeffrey liquid in an axisymmetric conduit having compliant walls and MHD effect to analyze the consequences of variable flow characteristics and slip conditions under peristalsis. It is noticed from their research work that velocity and temperature rise with the variable liquid parameter and the slip parameter.

Studies involving chemical reactions have earned the continuous involvement of the researchers. The reactions taking place in only one phase are homogeneous reactions and otherwise are termed heterogeneous. Reactions categorized by the properties of the reacting materials and that remain unaffected are called Homogeneous reactions. Distillation, air pollution, fog formation, ceramic production, fibrous insulation, combustion, catalysis, and numerous other procedures are due to homogeneous-heterogeneous reactions. The consequences of Carreau fluid transport in a conduit having Hall current and heterogeneous-homogeneous reactions are ascertained by Hayat et al. [10] considering wall properties under peristalsis. Their graphical depictions revealed that homogenous and heterogenous reaction parameters have a contradictory effect on the concentration profile. Analysis of homogeneous-heterogeneous reactions accompanied by heat source/sink and a radial magnetic field for a micropolar fluid's peristaltic motion is studied by Hayat et al. [11]. Their study indicated a decrease in pressure with the micropolar parameter; since the micro rotation parameter resists the flow, and the larger the magnetic field, the more is the resistance for the trapped bolus. Naveed et al. [12] inspected the Rabinowitsch fluid model's peristaltic transport involving thermal radiation to analyze chemical reactions' synchronized response. Their model finds application in the flow of blood under the consideration of chemical reactions and wall characteristics.

Research work carried on the peristaltic flow has, till recently, considered thermo-physical properties to be stable. But in reality, the temperature and velocity are seen to vary as in the case of blood. Even for lubricating fluids, the inner contacts produce instabilities in temperature, and in turn, the velocity is observed to change, thus implying that the fluid characteristics aren’t stable but varying. Hence it becomes vital to consider these effects. The features may differ regarding temperature diversity, indicatively: thermal conductivity and the variable viscosity. Variable properties uphold the wide association of biological and classical liquids. Samreen et al. [13] investigated the nanofluid flow in the symmetric vertical channel and have given relevance to the physical modeling of sinusoidal flow applicable in biomedical processes and industries. The study of variable liquid properties on the Rabinowitsch fluid model in an inclined porous peristaltic channel was studied by Hanumesh et al. [14] by considering the convective boundary conditions. The model helps in the design of peristaltic machinery and gives an outlook into the movement of chime and blood flow through micro arteries. The motion of Jeffery fluid under thermal conductivity and variable viscosity in a non-uniform porous conduit is inspected by Manjunatha et al. [15] to know the consequences of mass and heat transfer. The study indicates that fluid particles mainly concentrate near the channel walls; biologically, this is noticeable because the vital nutrients from biofluids disseminate to the adjoining cells and tissues. Hanumesh et al. [16] considered the motion in a complaint channel with porosity under convective conditions and variable thermal conductivity to carry on the Mass and Heat transport analysis of MHD peristaltic motion. The magnetic effect and the porosity variations on the velocity profile are nicely explained concerning blood flow in the human body. Variable thermal conductivity and viscosity affect the peristaltic mechanism of magneto-Carreau nano liquid having heat transfer irreversibilities is analyzed by Khan et al. [17]. Their study exposed the fact that the velocity is more for a Carreau nanomaterial with variable viscosity against the viscous nanomaterial.

The shear stress-deformation rate is linear for an ideal Bingham plastic, and it exhibits non-Newtonian behavior. Even though the velocity gradient is absent, these fluids have the potential to transmit shear stress. At low stresses, the fluid behaves like a rigid body, whereas at a high-stress level, the fluid acts like a viscous fluid. Bingham liquids have a thick covering in contrast to the Newtonian fluids. Printing ink, clay, toothpaste, paint, and edibles like mayonnaise, margarine, yogurts, ketchup, and melted chocolate are a few of the classic illustrations of Bingham fluids. Bingham fluids behave as a solid medium in the core layer, where the yield stress is more than the applied shear stress. This implies the movement of a solid plug in the channel. Practical applications of Bingham fluids can be seen in the shallow flow of soils and mud, avalanches, mucus in pulmonary airways, ceramics, and waxy crude oils. The Bingham fluid flow behavior under an inclined magnetic field effect is examined for mass and heat transfer effects by Akram et al. [18]. Pressure gradient and streamlines are depicted graphically for observing the impact of various parameters through different waveforms. Hayat et al. [19] studied Soret and Dufour characteristics on Bingham plastic's motion under peristalsis, applied with a magnetic field. Lakshminarayana et al. [20] considered an inclined porous channel to analyze the Bingham fluid behavior under Joule heating effects on the Peristaltic pumping. Validating their results under the absence of the Joule heating effect with the available results, they inferred that Joule heating helps the fluid velocity and increases the temperature.

Akram et al. [21] have graphically shown how the slip parameter helps increase the pressure rise in the upper half and decrease it in the lower half of the two-phase flow's peristaltic motion in the rectangular duct. Giving a clear vision of the harmonious relationship between the analytical and numerical solutions, Elmabound et al. [22] have elaborately explained the importance of gold nanoparticles in cancer treatment. With a high atomic number, the gold nanoparticles increase the temperature distribution that helps treat cancer disease. Recently, Javed et al. [23] have put forth the parameter effects on Herschel-Bulkley fluid transport mechanism on velocity, concentration, temperature, and heat transfer coefficients. Considering the Herschel Bulkley fluid under peristalsis, Javed et al. [24] explained graphically that the concentration is more for thinning fluid and less for thickening fluid while analyzing the flow in a two-dimensional non-uniform flexible conduit. The homogenous-heterogenous reaction effects on Sutterby fluid’s motion considered for analysis by Naveed et al. [25] revealed that they behave conversely on the concentration profile. Naveed et al. [26] have studied the Rabiniwitsch fluid coupled with chyme motion to analyze the effects in the human body. Their study explores the impact of different parameters on shear thinning, shear thickening, and viscous fluid models. They noted that the momentum and thermal distributions behave oppositely for stiffness, rigidity, and viscous damping force parameters.

Driven by the above studies, a Bingham fluid's flow behavior in a compliant walled peristaltic channel is modeled to analyze the homogeneous and heterogeneous reactions when subjected to variable liquid properties. Besides this, the MHD effect, along with non-uniform geometry under the partial velocity slip, is examined. The MATLAB programming is used to obtain the solution of the governing equations under the lubrication approach.

Section 2 deals with the Formulation of the problem and its solution methodology is described under Sect. 3. A detailed analysis of the results is explained with graphical representations in Sect. 4. Section 5 summarizes the article with concluding remarks. The Nomenclature and "Appendix" are attached at the end of the article before the Reference Section.

2 Formulation of the problem

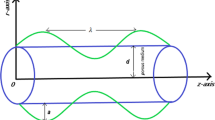
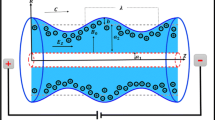
The 2-D motion of an electrically conducting Bingham fluid in a non-uniform channel inclined to the horizontal at an angle $\alpha$ is considered (See Fig. 1). Further, the wall properties (complaint walls) along with the chemical reactions are taken into account. The wave-like motions provoked by the peristaltic motion transmits the fluid with constant speed through the symmetric channel. The liquid is assumed to pass through a transverse magnetic field, and the induced magnetic field becomes insignificant as we assume a low Reynolds number approximation.

Fig. 1

Physical model representing the flow geometry

As the liquid progresses into the magnetic field, two significant physical impacts emerge. Firstly, an electric field $E$ is prompted in the stream. Since there is no ample charge thickness, subsequently,$\nabla .E = 0$. The induced electric field becomes unimportant as $\nabla \times E = 0$, ignoring the induced magnetic field. The subsequent impact is progressive, i.e., a Lorentz force $(J \times B_{1} )$, where the current density is $J$, follows up on the liquid and changes its movement. This results in the exchange of energy to the fluid from the electromagnetic field. In the current investigation, the relativistic impacts are ignored, and Ohm's law gives the current density $J$ as [8]

$$J = \sigma \left( {\overline{V} \times B_{1} } \right)$$

(1)

where $\sigma$ is the electrical conductivity and $\overline{V}$ is the velocity field.

The homogeneous-heterogeneous reaction model between the chemical species $A$ and $B$ is represented as [11]:

$$A + 2B \to 3B,\,\,\,\,\,\,{\text{rate}} = k_{c} \overline{\zeta } \overline{\varphi }^{2} .$$

(2)

Considering the single, first-order and isothermal reaction on the catalyst, we have

$$A \to B,\,\,\,\,\,\,{\text{rate}} = k_{s} \overline{\zeta } ,$$

(3)

where the concentrations of $A$ is $\overline{\zeta }$ and $B$ is $\overline{\varphi }$, and $k_{c}$ and $k_{s}$ are the rate constants. Notice that the two reactions take place at an identical temperature.

The channel wall deformation due to the peristalsis is [15]

$$\overline{h} \,\,(\overline{X} ,\overline{t} ) = l(\overline{X} ) + b\,\,{\text{Sin}} \left[ {\frac{2\pi }{\lambda }\left( {\overline{X} - c\overline{t} } \right)} \right],$$

(4)

Here $l(\overline{X} )$ is the non-uniform channel width, $t$ is the time and $b$ is the wave amplitude.Then considering $\overline{U}$ and $\overline{V}$ as respectively the $\overline{X}$ and $\overline{Y}$ components of the fluid velocity, equations that govern the flow are:

$$\frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \frac{{\partial \overline{V} }}{{\partial \overline{Y} }} = 0,$$

(5)

$$\rho \left( {\frac{{\partial \overline{U} }}{{\partial \overline{t} }} + \overline{U} \frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \overline{V} \frac{{\partial \overline{U} }}{{\partial \overline{Y} }}} \right) = - \frac{{\partial \overline{P} }}{{\partial \overline{X} }} + \frac{{\partial \overline{\tau }_{{_{{\overline{X} \overline{X} }} }} }}{{\partial \overline{X} }} + \frac{{\partial \overline{\tau }_{{_{{\overline{X} \overline{Y} }} }} }}{{\partial \overline{Y} }} - \sigma_{1} B_{0}^{2} \overline{U} + \rho g\,\,{\text{Sin}} \alpha ,$$

(6)

$$\rho \left( {\frac{{\partial \overline{V} }}{{\partial \overline{t} }} + \overline{U} \frac{{\partial \overline{V} }}{{\partial \overline{X} }} + \overline{V} \frac{{\partial \overline{V} }}{{\partial \overline{Y} }}} \right) = - \frac{{\partial \overline{P} }}{{\partial \overline{Y} }} + \frac{{\partial \overline{\tau }_{{_{{\overline{X} \overline{X} }} }} }}{{\partial \overline{X} }} + \frac{{\partial \overline{\tau }_{{_{{\overline{X} \overline{Y} }} }} }}{{\partial \overline{Y} }} - \rho g\,\,{\text{Cos}} \alpha ,$$

(7)

$$\rho c_{p} \left( {\frac{{\partial \overline{T} }}{{\partial \overline{t} }} + \overline{U} \frac{{\partial \overline{T} }}{{\partial \overline{X} }} + \overline{V} \frac{{\partial \overline{T} }}{{\partial \overline{Y} }}} \right) = \frac{\partial }{{\partial \overline{X} }}\left( {k(\overline{T} )\frac{{\partial \overline{T} }}{{\partial \overline{X} }}} \right) + \frac{\partial }{{\partial \overline{Y} }}\left( {k(\overline{T} )\frac{{\partial \overline{T} }}{{\partial \overline{Y} }}} \right) + \,\overline{\tau }_{{_{{\overline{X} \overline{X} }} }} \frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \overline{\tau }_{{_{{\overline{Y} \overline{Y} }} }} \frac{{\partial \overline{V} }}{{\partial \overline{Y} }} + \overline{\tau }_{{_{{\overline{X} \overline{Y} }} }} \left( {\frac{{\partial \overline{V} }}{{\partial \overline{X} }} + \frac{{\partial \overline{U} }}{{\partial \overline{Y} }}} \right),$$

(8)

$$\frac{d\zeta }{{d\overline{t} }} = M_{A} \left( {\frac{{\partial^{2} \zeta }}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} \zeta }}{{\partial \overline{Y}^{2} }}} \right) - K_{c} \zeta \varphi^{2} ,$$

(9)

$$\frac{d\varphi }{{d\overline{t} }} = M_{B} \left( {\frac{{\partial^{2} \varphi }}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} \varphi }}{{\partial \overline{Y}^{2} }}} \right) + K_{c} \zeta \varphi^{2} ,$$

(10)

where $\overline{\tau }_{{_{{\overline{X} \overline{X} }} }}$, $\overline{\tau }_{{_{{\overline{X} \overline{Y} }} }}$ and $\overline{\tau }_{{_{{\overline{Y} \overline{Y} }} }}$ represent the extra stress components,$\rho$: the density of the fluid, $\overline{T}$: the temperature of the liquid, $k(\overline{T} )$: the thermal conductivity, $c_{p}$: the specific heat capacity at a constant pressure.

The flexible motion of the wall is mathematically given by [12]

$$L(h) = P - P_{0} ,$$

(11)

Here $P_{0} ( = 0)$ represents the outer wall pressure due to the muscle tension. The linear operator $L$ signifies stretching of the membrane appended by the focus of viscous damping and is given by

$$L = - \tau \frac{{\partial^{2} }}{{\partial x^{2} }} + m_{1} \frac{{\partial^{2} }}{{\partial t^{2} }} + n_{1} \frac{\partial }{\partial t},$$

(12)

where $n_{1}$ is the viscous damping coefficient, $m_{1}$ denotes the mass per unit area and $\tau$ denotes the elastic tension.

$$\frac{\partial p}{{\partial x}} = E_{1} \frac{{\partial^{3} h}}{{\partial x^{3} }} + E_{2} \frac{{\partial^{3} h}}{{\partial t^{2} \partial x}} + E_{3} \frac{{\partial^{3} h}}{{\partial t\partial x^{2} }}.$$

(13)

If the velocity components are $(\overline{u} ,\overline{v} )$ and the coordinates represented as $(\overline{x} ,\overline{y} )$ in the wave frame $(\overline{x} ,\overline{y} )$ then,

$$\overline{x} = \overline{X} - c\overline{t} ,\,\,\overline{y} = \overline{Y} ,\,\,\,\overline{u\,} (\overline{x} ,\overline{y} ) = \overline{U} (\overline{X} ,\overline{Y} ,\overline{t} ) - c,\,\overline{v} \,(\overline{x} ,\overline{y} ) = \overline{V} (\overline{X} ,\overline{Y} ,\overline{t} ),\,\,\,\overline{T} (\overline{x} ,\overline{y} ) = \overline{T} (\overline{X} ,\overline{Y} ,\overline{t} ),\,\,\overline{p} \,(\overline{x} ,\overline{y} ) = \overline{P} (\overline{X} ,\overline{Y} ,\overline{t} ).$$

(14)

The dimensionless quantities are

$$\begin{gathered} x = \frac{{\overline{x} }}{\lambda },\,\,\,\,\,\,y = \frac{{\overline{y} }}{{l_{2} }},\,\,\,\,\,\,u = \frac{{\overline{u} }}{c},\,\,\,\,\,\,v = \frac{{\overline{v} }}{c\delta },\,\,\,\,\,\,c_{p} = \frac{{l_{2} }}{\lambda },\,\,\,\,\,\,p^{\prime} = \frac{{pl_{2}^{2} }}{{\mu_{0} \lambda c}},\,\,\,\,\,{\text{Re}} = \frac{{l_{2} c}}{\vartheta },\,\,\,\,\,\vartheta = \frac{{\mu_{0} }}{\rho },\,\,\,\,\,M = \sqrt {\frac{{\sigma_{1} }}{{\mu_{0} }}} B_{0} l_{2} , \hfill \\ \tau_{xx} = \frac{{l_{2} \overline{\tau }_{xx} }}{{\mu_{0} c}},\,\,\,\,\,\,\,\varepsilon = \frac{b}{{l_{2} }},\,\,\,\,\,\,\,t = \frac{{\overline{t} c}}{\lambda },\,\,\,\,\,\,\,\tau_{xy} = \frac{{l_{2} \overline{\tau }_{xy} }}{{\mu_{0} c}},\,\,\,\,\,\,\,\tau_{yy} = \frac{{l_{2} \overline{\tau }_{yy} }}{{\mu_{0} c}},\,\,\,\,\,\,\,\psi ^{\prime} = \frac{\psi }{{l_{2} c}},\,\,\,\,\,\,\xi = \frac{{M_{A} }}{{M_{B} }},\,\,\,\,\,\,Sc = \frac{{\mu_{0} }}{{\rho M_{A} }}, \hfill \\ \mu_{0} = \frac{{\overline{\mu }_{0} }}{\mu },\,\,\,\,\,\,E_{1} = \frac{{ - \tau l_{2}^{3} }}{{\lambda \mu_{0}^{3} c}},\,\,\,\,\,\,\,\Pr = \frac{{\mu_{0} c_{p} }}{{k_{0} }},\,\,\,\,\,\,E_{1} = \frac{{ - \tau l_{2}^{3} }}{{\mu_{0} \lambda^{3} c}},\,\,\,\,\,\,E_{2} = \frac{{m_{1} l_{2}^{3} c}}{{\mu_{0} \lambda^{3} }},\,\,\,\,\,E_{3} = \frac{{n_{1} l_{2}^{3} }}{{\mu_{0} \lambda^{3} }},\,\,\,\,\,\theta = \frac{{T - T_{0} }}{{T_{0} }},\,\,\, \hfill \\ Ec = \frac{{c^{2} }}{{c_{p} T_{0} }},\,\,\,\,\,\overline{\zeta } = \frac{f}{{\zeta_{0} }},\,\,\,\,\,\overline{\varphi } = \frac{g}{{\zeta_{0} }},\,\,\,\,\,l(\overline{x} ) = l_{2} + m\,(\overline{x} ),\,\,\,\,\,\,F = \frac{\vartheta c}{{gl_{2}^{2} }},\,\,\,\,\,\,\,h = \,\frac{{\overline{h} }}{{l_{2} }} = 1 + \frac{\lambda \,m\,x}{{l_{2} }} + \varepsilon \sin (2\pi (x - t)). \hfill \\ \end{gathered}$$

(15)

Using Eqs. (14) and (15) in the Eqs. (5–10) and applying Lubrication theory the governing equations are nondimensionalised and are given by:

$$\frac{\partial p}{{\partial x}} = \frac{{\partial \tau_{xy} }}{\partial y} + \frac{{{\text{Sin}}\,\alpha }}{F} - M^{2} (u + 1),$$

(16)

$$\frac{\partial p}{{\partial y}} = 0,$$

(17)

$$\frac{\partial }{\partial y}\left( {k(\theta )\frac{\partial \theta }{{\partial y}}} \right) + Br\,\tau_{xy} \left( {\frac{\partial u}{{\partial y}}} \right) = 0,$$

(18)

$$\frac{1}{Sc}\frac{{\partial^{2} f}}{{\partial y^{2} }} - Kfg^{2} = 0,$$

(19)

$$\frac{\xi }{Sc}\frac{{\partial^{2} g}}{{\partial y^{2} }} + Kfg^{2} = 0,$$

(20)

where $\tau_{xy}$ represents the fundamental equation of Bingham fluid, represented as (see Ref. [18])

$$\tau_{xy} = \mu (y)\frac{\partial u}{{\partial y}} + \tau_{0} \,\,for\,\,\tau \ge \tau_{0} ,$$

(21)

$$\tau_{xy} = 0\,\,for\,\,\tau \le \tau_{0} ,$$

(22)

where $\tau_{0}$ is the yield stress and $\mu (y)$ is the variable viscosity.

In one day, a similar sized animal or person on an average takes one to two litres of the fluid. Added to this, the pancreas, salivary glands, small intestine, liver and stomach produce secretions which amount to about six to seven litres of the fluid are collected by the small intestine. This brings out the reliance on fluid concentration upon the spatial coordinate $y$.

It is also observed that the concentration of the blood cells in the arteries is more at the centre and the walls are covered by a thin layer of clear plasma Hence the viscosity of the fluid is less at the walls and increases as we move away from the wall. Further, the well-known fact is that the thermal conductivity varies with reference to the temperature (See [15] for details).

The expressions for variable viscosity is:

$$\mu (y) = 1 - \alpha_{1} y\,\,\,\,for\,\,\,\,\alpha_{1} < < 1,$$

(23)

The expression for thermal conductivity is:

$$k(\theta ) = 1 + \gamma \theta \,\,\,\,\,for\,\,\,\,\,\gamma < < 1,$$

(24)

Where $\alpha_{1}$ represents the coefficient of viscosity and $\gamma$ the coefficient of thermal conductivity.

The dimensionless peripheral conditions are subsequently:

$$\,u + \frac{{\sqrt {Da} }}{\beta }\frac{\partial u}{{\partial y}} = - 1;\,\frac{\partial \theta }{{\partial y}} + Bi\theta = 0\,\,at\,\,y = h = 1 + mx + \varepsilon \sin \left[ {2\pi (x - t)} \right],$$

(25)

$$\frac{\partial f}{{\partial y}} = K_{s} f;\,\frac{\partial g}{{\partial y}} = - K_{s} f\,\,at\,\,y = h = 1 + mx + \varepsilon \sin \left[ {2\pi (x - t)} \right],$$

(26)

$$\frac{\partial u}{{\partial y}} = \tau_{0} ;\,\,\frac{\partial \theta }{{\partial y}} = 0\,\,\,at\,\,\,\,y = 0,$$

(27)

$$f = 1;\,\,g = 0\,\,\,at\,\,\,\,y = 0.$$

(28)

The diffusion constants $M_{A}$ and $M_{B}$ are assumed to be same (i.e. $\xi = 1$), which makes Eqs. 26 and 28 take the following form:

$$f + g = 1.$$

(29)

Using the above, Eqs. 19 and 20 can be written as

$$\frac{1}{Sc}\frac{{\partial^{2} f}}{{\partial y^{2} }} = Kf(1 - f)^{2} .$$

(30)

Considering the conditions at the boundary

$$f = 1\,\,\,\,{\text{at}}\,\,\,\,y = 0,$$

(31)

$$\frac{\partial f}{{\partial y}} = K_{s} f\,\,{\text{at}}\,\,\,\,y = h.$$

(32)

3 Method of solution

Equation (16) along with boundary conditions (25) and (27), are solved analytically to get a solution for the velocity filed

$$u = \frac{1}{{8M^{3} (L_{0} )^{2} }}(8ML_{0} \,L_{27} + \cosh (My)(2\beta L_{22} + L_{23} + ML_{24} \tau_{0} )\alpha_{1} + L_{28} + M\tau_{0} (L_{25} + L_{26} )).$$

(33)

where

$$P = \frac{\partial p}{{\partial x}} = 4\varepsilon \pi^{2} \left[ { - 2\pi \,\cos [2\pi (x - t)](E_{1} + E_{2} ) + \sin [2\pi (x - t)]E_{3} } \right]\;{\text{and}}\;f = \frac{\sin \,\alpha }{F}$$

(34)

The stream function $\psi$ is found by integrating Eq. (33) using the condition $\psi = 0\,\,at\,y = 0$,

$$\psi = \frac{1}{{8M^{4} (L_{0} )^{2} }}(8M\,L_{0} L_{4} + L_{9} + M\,\tau {}_{0}\,L_{21} ).$$

(35)

The temperature and homogeneous/heterogeneous equations being non-linear are difficult to solve for obtaining a closed form solution. Therefore, the perturbation method is opted to get the solution. The variable thermal conductivity $(\gamma )$ and the homogeneous reaction parameter $(K)$ are taken as the perturbation parameters for finding concentration profile and temperature, respectively ([12] and [15]):

$$\theta = \theta_{0} + \gamma \theta_{1} + \gamma^{2} \theta_{2} + O(\gamma^{3} ),$$

(36)

$$f = f_{0} + Kf_{1} + K^{2} f_{2} + O(K^{3} ).$$

(37)

3.1 Zeroth order system for temperature

$$\frac{\partial }{\partial y}\left( {k(\theta_{0} )\frac{{\partial \theta_{0} }}{\partial y}} \right) + Br\,\tau_{xy} \left( {\frac{\partial u}{{\partial y}}} \right) = 0,$$

(38)

$$\,\frac{{\partial \theta_{0} }}{\partial y} + Bi\,\theta_{0} = 0\,\,\,at\,\,y = h\,\,,$$

(39)

$$\,\frac{{\partial \theta_{0} }}{\partial y} = 0\,\,\,\,\,\,at\,\,\,\,y = 0.$$

(40)

3.2 First order system for temperature

$$\frac{\partial }{\partial y}\left( {k(\theta_{1} )\frac{{\partial \theta_{1} }}{\partial y}} \right) + Br\,\tau_{xy} \left( {\frac{\partial u}{{\partial y}}} \right) = 0,$$

(41)

$$\,\frac{{\partial \theta_{1} }}{\partial y} + Bi\,\theta_{1} = 0\,\,\,\,at\,\,y = h\,\,,$$

(42)

$$\,\frac{{\partial \theta_{1} }}{\partial y} = 0\,\,\,\,\,\,at\,\,\,\,y = 0.$$

(43)

On solving zeroth and first-order system, we get $\theta = \theta_{0} + \gamma (\theta_{0} )^{2}$ whose expression is obtained through the MATLAB 2019b software for analysis.

3.3 Zeroth order system for concentration

$$\frac{1}{Sc}\frac{{\partial^{2} f_{0} }}{{\partial y^{2} }} = Kf_{0} (1 - f_{0} )^{2} ,$$

(44)

$$\frac{{\partial f_{0} }}{\partial y} = K_{s} f_{0} ;\,\,\,\frac{\partial g}{{\partial y}} = - K_{s} f_{0} \,\,at\,\,y = h\,\,,$$

(45)

$$\,f_{0} = 1\,\,;\,\,\,g = 0\,\,\,at\,\,y = 0.$$

(46)

3.4 First order system for Concentration

$$\frac{1}{Sc}\frac{{\partial^{2} f_{1} }}{{\partial y^{2} }} = Kf_{1} (1 - f_{1} )^{2} ,$$

(47)

$$\frac{{\partial f_{1} }}{\partial y} = K_{s} f_{1} ;\,\,\,\frac{\partial g}{{\partial y}} = - K_{s} f_{1} \,\,at\,\,y = h\,\,,$$

(48)

$$\,f_{1} = 1;\,\,g = 0\,\,\,at\,\,y = 0.$$

(49)

Zeroth and first order systems are solved and the expression for concentration is obtained by substituting them in the perturbation Eq. (37). The Matlab 2019b programming has been used to analyze the impact of various parameters on it.

4 Results and discussion

This segment analyzes the consequences of velocity $(u)$, temperature $(\theta )$, concentration $(f)$ and streamlines $(\psi )$ via graphical depictions. Particularly the nature of the impact on the wall parameters $(E_{1} ,\,\,E_{2} ,\,\,E_{3} )$, homogeneous-heterogeneous reaction parameters ($k$ and $k_{s}$), magnetic parameter $(M)$, variable viscosity $(\alpha_{1} )$,Darcy number $(Da)$,Schmidt number $(Sc)$, non-uniform parameter $(m)$, yield stress $(\tau_{0} )$, Biot number $(Bi)$, Angle of inclination $(\alpha )$ and partial slip parameter $(\beta )$ are analyzed.

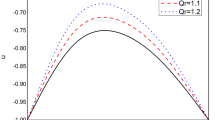
Effects of the axial velocity on different parameters have been plotted and are shown in Figs. 2, 3 and 4. Change in the coefficient of variable viscosity slightly increases the flow velocity, as seen in Fig. 2a. As viscosity lessens with growing values of $\alpha_{1}$, successively, this boosts the velocity of the fluid. Increasing the magnetic parameter lowers the velocity, as depicted in Fig. 2b. The flow of a radially directed magnetic field reduces the fluid flow. The study of blood flow inside the arteries can be emphasized through the reflection of flow through porous walls. It is clear from Fig. 2c that the rise in Darcy number Da slightly improves the flow velocity. Figure 2d illustrates that the velocity reduces by increasing the partial slip parameter $\beta$. The pictorial representation of the effect of elastic parameters $E_{1} \,\,{\text{and}}\,\,E_{2}$ on the flow velocity exhibits the physical nature of the flexible wall. The least resistance offered to the fluid motion and can be seen from the graphical depictions. Figure 3a and b shows growth in velocity for rise in the values of the elastic parameters $E_{1} \,\,{\text{and}}\,\,E_{2}$ in the non-uniform channel. Conversely, the flow velocity becomes less as the damping wall parameter $E_{3}$ increases and supports the physical interpretation that dampness makes a deprived effect on the velocity (Fig. 3c). The variable viscosity parameter's similar behavior can be visualized in the research findings of [9] and [14]. Magnetic parameter and the wall property effects on the velocity profile match with the graphical representations of [9] and [20]; hence our results can be justified. Examination of Fig. 4a puts forth that enhancing the yield stress reduces the velocity. Figure 4b exposes that the fluid velocity accelerates with the non-uniform parameter. This result agrees with the result of [20]. Figure 4c discloses the effect of elevation in the magnetic field's inclination angle and infers that the velocity profile comes down at the walls but increases in the mid-region of the channel.

Fig. 2

Plots of velocity for different values of a variable viscosity, b magnetic parameter, c permeable parameter and d partial velocity slip parameter

Fig. 3

Plots of velocity for different values of elastic parameters

Fig. 4

Plots of velocity for different values of a yield stress parameter, b non-uniform parameter and c angle of inclination parameter

Plots in Fig. 5a–d explain the response of various parameters on temperature. Figure 5a specifies the reduction of velocity with a rise in the variable viscosity. Analysis of Fig. 5b reveals the growth in temperature with ascending values of variable thermal conductivity. It is known that the fluid’s thermal conductivity gives the amount of the liquid’s capacity to preserve or liberate heat in its neighborhood. Hence, the thermal value of the liquid increases when the fluid’s thermal conductivity inside the channel is more than the temperature of the wall. Similar analyses done by [9] on the Jeffery fluid The growing deviation in the magnetic parameter diminishes the measure of temperature, as noticed from Fig. 5c, due to the restraining nature of the magnetic field. This result agrees with the results of [9] and [18]. Figure 5d clarifies that increasing Biot number reduces the temperature profile since increment in the Biot number lowers the thermal conductivity and contributes to the fall in the temperature profile.

Fig. 5

Plots of temperature for different values of a variable viscosity, b variable thermal conductivity, c magnetic parameter and d Biot number

The concentration profile behaves converse to the temperature profile, which is physically reasonable because heat and mass are known to behave contrarily. Plots in Fig. 6a–d highlight the effects of various parameters on the concentration distribution. The graph in Fig. 6a shows the reducing affect on the concentration distribution as the homogeneous reaction parameter strengthens. On the other hand, the reverse behavior is noticed with the heterogeneous reaction parameter variation and is depicted in Fig. 6b. Figure 6c gives evidence that an increasing nonuniform parameter declines the concentration distribution. The outcomes of Schmidt number on $f(y)$ is shown in Fig. 6d. In agreement with the results of [9] the graph shows reduction in concentration distribution, which holds on to the feature that the mass of fluid particles decreases with the Schmidt number and promotes the fluid transport. Thus it can be inferred that the fluid particles having less density promotes the speed and acquire higher molecular vibrations that decrease the concentration of the liquid. This result is in agreement with the results of [16].

Fig. 6

Plots of f(y) for different values of a homogeneous reaction, b heterogeneous reaction, c non-uniform parameter and d Schmidt number

The streamlines play a vital role in understanding the movement of the bolus through biological organs. Specifically, it helps in understanding the chime movement in the gastrointestinal tract and the thrombus formation. The variation in the variable viscosity slightly enhances the size of the bolus, as observed in Fig. 7, and the result is in agreement with [9]. It is noticed that the magnetic parameter shrinks the bolus from Fig. 8, which matches with the result of [18]. Thus, it is possible to control the formation of bolus with an increase/decrease in variable viscosity and magnetic parameter.

Fig. 7

Streamlines for varying variable viscosity when a $\alpha_{1} = 0.01$ and b $\alpha_{1} = 0.03$

Fig. 8

Streamlines for varying magnetic parameter when a $M = 1.5$ and b $M = 2$

5 Conclusions

The consequences of variable liquid properties on the MHD peristaltic flow of Bingham fluid are detailed in this analysis. The heat and mass transfer features are inspected through convective and wall property effects in a non-uniform, inclined channel having permeable walls. The solution obtained under the assumptions of low Reynolds number and long wavelength are graphically plotted through MATLAB and analyzed. Velocity, Temperature and concentration profiles are discussed for variations in different parameters. Stream lines are drawn to understand the bolus movement in biological organs.

The present article emphasizes the characteristics of peristaltic waves under heat and mass transfer with varying parameters that helps in understanding the behavior of blood when it is exposed to an external magnetic field. This may help in improving the design of peristaltic pumping instruments in medical engineering and also in industries. The paper can be extended to study the entropy generation under variable liquid properties.

Appendix

$$L_{0} = \beta \cosh (hM) + \sqrt {Da} M\sinh (hM)$$

$$L_{1} = 4M^{2} - (f - P)(h + y)$$

$$L_{2} = 4M^{2} - (f - P)(3h + y)$$

$$L_{3} = - \beta ( - 1 + h^{2} M^{2} )(f - P) + \sqrt {Da} \,M^{2}$$

$$L_{4} = M( - f + M^{2} + P)\,y\,L_{0} + \beta (f - P)\sinh (My)$$

$$L_{5} = M( - f + M^{2} + P)\,y\,L_{0} + \beta (f - P)\sinh (My)$$

$$L_{6} = M(\sqrt {Da} \,h^{2} M^{2} (P - f))$$

$$L_{7} = 4\beta \sqrt {Da} \,h\,M^{2} + Da\,M^{4} ( - 2h^{2} + y^{2} ) + \beta^{2} ( - 2 + M^{2} (2h^{2} - y^{2} ))$$

$$L_{8} = \beta^{2} - Da\,M^{2}$$

$$L_{9} = 2\beta (M^{2} (f - P)y^{2} \cosh (My)L_{0} + L_{6} + \beta \,M\,L_{1} \cosh (hM) + (L_{3} L_{2} \sinh (hM))\,\sinh (My))\,\alpha_{1}$$

$$L_{10} = \beta^{2} + Da\,M^{2}$$

$$L_{11} = - 4\,L_{10} + ((y - 4)L_{10} + 2\beta \sqrt {Da} M^{2} y^{2} )\,\alpha_{1}$$

$$L_{12} = - 8\beta \sqrt {Da} + (2\beta \sqrt {Da} ( - 4 + y) + L_{10} y^{2} )\alpha_{1}$$

$$L_{13} = M(\cosh (M(2h - y))L_{11} + M\sinh (M(2h - y))L_{12} )$$

$$L_{14} = L_{6} + M\beta ( - fh + 4M^{2} + hP)\cosh (hM) + L_{3} ( - 3fh + 4M^{2} + 3hP)\sinh (hM)$$

$$L_{15} = \cosh (M(2h - y_{0} ))$$

$$L_{16} = \sinh (M(2h - y_{0} ))$$

$$L_{17} = 2(\beta^{2} - \beta \,h(2\sqrt {Da} + \beta \,h)M^{2} + Da\,h^{2} M^{2} )\sinh (My_{0} )$$

$$L_{18} = L_{15} (3L_{10} - 2\beta \sqrt {Da} M^{2} y_{0} ) - M\,L_{16} ( - 6\beta \sqrt {Da} \, + L_{10} y_{0} ) + L_{8} (3\cosh (My_{0} ) + M\sinh (My_{0} )y_{0} )$$

$$L_{19} = 4M(4L_{10} \,L_{15} M(L_{8} \,\cosh (My_{0} ) + 2\beta \sqrt {Da} \,M\,L_{16} ) + L_{17} + My_{0} L_{18} )$$

$$L_{20} = - 1 + y^{2} M^{2}$$

$$L_{21} = L_{7} \sinh My\,\alpha_{1} + M\,L_{8} \,\cosh My\,( - 4 + (y - 4)\alpha_{1} ) + L_{13}$$

$$L_{22} = ( - L_{6} + M\beta ( - 4M^{2} + (f - P)(h - y)))\cosh (hM)$$

$$L_{23} = (\beta ( - 1 + h^{2} M^{2} )(f - P)\, + \sqrt {Da} \,M^{2} ( - 4M^{2} + (f - P)(3h - y)))\sinh (hM)$$

$$L_{24} = Da\,M^{2} - 4\beta \sqrt {Da} \,h\,M^{2} + Da\,M^{4} (2h^{2} - y^{2} )\, + \beta^{2} (1 - M^{2} 2h^{2} y^{2} )$$

$$L_{25} = M\,\sinh (M(2h - y))( - 4L_{10} - ((4 + y)L_{10} - 2\beta \sqrt {Da} \,L_{20} )\alpha_{1} )$$

$$L_{26} = \cosh (M(2h - y))( - 8\beta M^{2} \sqrt {Da} + ( - 2\beta \sqrt {Da} M^{2} (4 + y) + \beta^{2} L_{20} + Da\,M^{2} L_{20} )\alpha_{1} )$$

$$L_{27} = \beta (P - f)\cosh (My) - (P - f + M^{2} )L_{0}$$

$$L_{28} = \sinh (My)( - 2\beta (f - P)L_{20} L_{0} \alpha_{1} + M^{2} L_{8} \,\tau_{0} (4 + (4 + y)\alpha_{1} ))$$

$$L_{29} = 2\beta (4M(f - P)L_{0} \sinh (My_{0} ) + (L_{14} \sinh (My_{0} ) + (f - P)L_{0} \,y_{0} (3\sinh (My_{0} ) + M\cosh (My_{0} )y_{0} ))\alpha_{1} )$$

$$L_{30} = M(4M(L{}_{10}L_{15} + L_{8} \cosh (My_{0} ) + 2\beta \sqrt {Da} \,M\,L_{16} ) + L_{19} \alpha_{1} )$$

$$\tau_{0} = \frac{{L_{29} }}{{L_{30} }}.$$